三角函数的概念(苏教版)
图片预览




文档简介
三角函数的概念,同角三角函数的关系和诱导公式
知识的梳理
角的概念的推广
定义:一条射线由原来的位置,绕着它的端点按一定方向旋转到另一个位置,就形成了角,角分为正角,零角,负角。
象限角;
第一象限角:;
第二象限角:;
第三象限角:;
第四象限角:;
终边相同的角:一般地,所有与角终边相同的角连同角在内,可以表示为
二;弧度
1定义:用“弧度”作单位来度量角的制度,叫做弧度制。
2.角度与弧度的互化:
3,两个公式:(R为圆弧半径,为圆心角的弧度数)
扇形弧式:扇形面积公式:
三 三角函数的定义
1.定义:设是一个任意角,角的终边上任意一点,它与原点的距离为,那么角的正弦、余弦、正切分别是: 它们都是以角为自变量,以比值为函数值的函数
2 .三角函数在各象限内的符号口诀是:一全正;二正弦;三正切;四余弦;
3.同角三角函数的基本关系式
1)平法关系:
2)商数关系:
3)倒数关系:
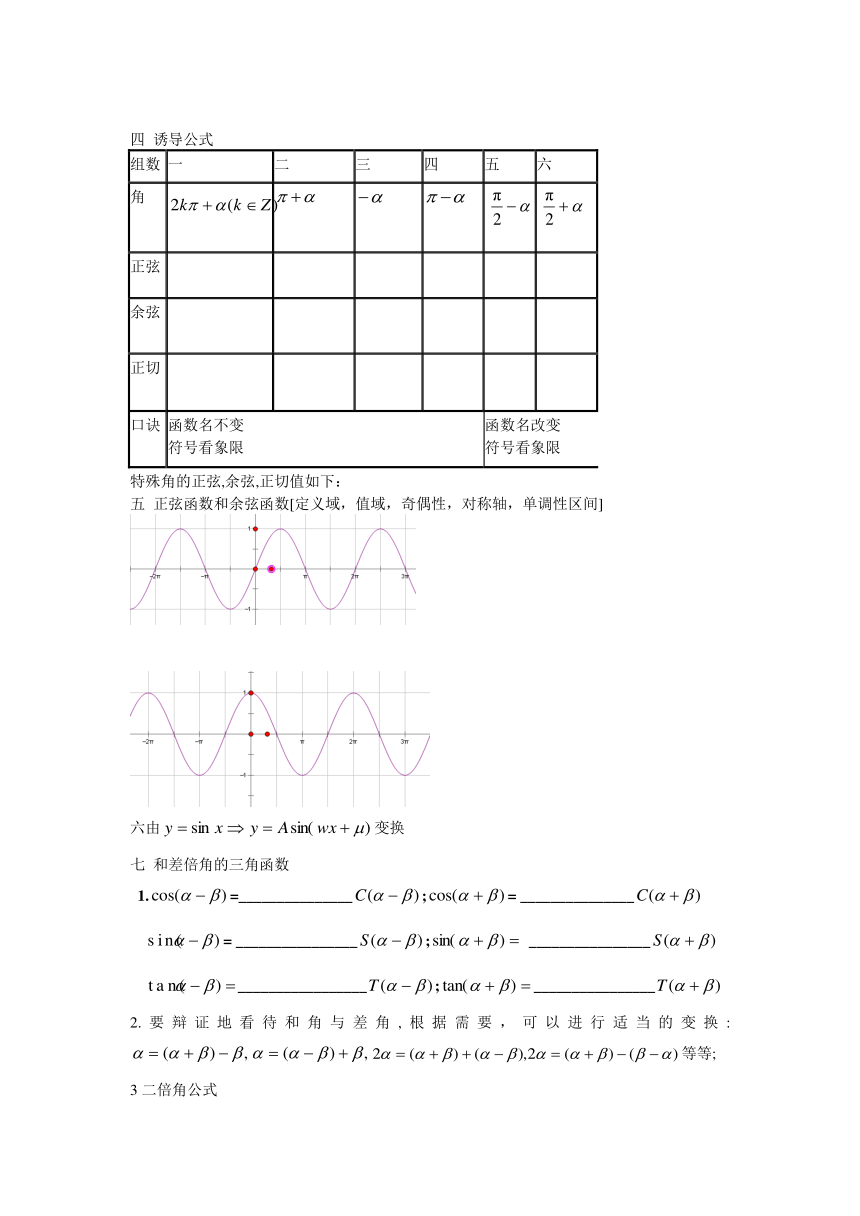
四 诱导公式
组数 一 二 三 四 五 六
角
正弦
余弦
正切
口诀 函数名不变符号看象限 函数名改变符号看象限
特殊角的正弦,余弦,正切值如下:
五 正弦函数和余弦函数[定义域,值域,奇偶性,对称轴,单调性区间]
六由变换
七 和差倍角的三角函数
1.=_______________;= _______________
= ________________; ________________
_________________;________________
2.要辩证地看待和角与差角,根据需要,可以进行适当的变换: 等等;
3二倍角公式
= ________________=_______________ ;
4.在准确熟练地记住公式的基础上,要灵活运用公式解决问题:如公式的正用、逆用和变形用等.如T(α±β)可变形为:
5.函数,可以化为_______________;其中可由a,b的值唯一确定
八:三角函数的图象与性质
1.周期函数
(1)周期函数的定义
对于函数f(x),如果存在一个非零常数T,使得定义域内的每一个x值,都有.那么函数f(x) 就叫做周期函数。非零常数T叫做这个函数的周期.
(2)最小正周期
如果在周期函数f(x)的所有周期中存在一个最小正数,那么这个最小正数就叫做f(x)的最小正周期.
思考:如果函数y=f(x)的周期是T,那么函数y=f(ωx)的周期是多少?
例1如果为第一象限角,试问:是第几象限角?
例2已知一扇形的圆心角是,所在圆的半径是R.
若,求扇形的弧长及该弧所在的弓形的面积;
若扇形的周长是一定值,当为多少弧度时,该扇形有最大面积?
例3函数的值域是___________
例4求下列函数的定义域:
(1)
(2)
例5已知,求下列各式的值
(1)
(2)
变式 已知,求的值;
例6已知,求的值;
例7已知是关于的方程的两根;
求的值;
求的值;
例8已知函数
求的值
求的最大值和最小值;
变式1已知函数的定义域为,函数的最大值为1,最小值为,求和的值;
变式2 已知函数(其中的图像与x轴的交点中,相邻两个交点之间的距离为,且图像上一个最低点为.
求的解析式;
当时,求的值域;
例9将函数的图像上所有点向右平行移动个单位长度,在把所有各点的横坐标伸长到原来的2倍(纵坐标不变),所得图像的函数解析式是____________________
变式若函数的图像向右平移个单位长度后,与函数的图像重合,则的最小值为____________
例10已知函数)在时取得最大值4;
求的最小正周期;
求的解析式;
若,求;
变式已知函数;
求函数的最小正周期和图像的对称轴方程;
求函数在区间上的值域;
例11已知,求的值。
变式已知那么的值;
1. 的值是_____.
2.已知为第二象限角,且则
3.若则
4.已知 且α则
5若函数在区间上单调递增,在区间上单调递减,则
6设函数,将的图像向右平移个单位长度后,所得的图像与原图像重合,则的最小值等于________________
7已知函数,若,则x的取值范围为_______________
8设,则
9若,则的值等于_______________.6
10函数的最大值为_____________
11已知 则的值为__________
12已知函数。
(Ⅰ)求的最小正周期:
(Ⅱ)求在区间上的最大值和最小值。
解:(Ⅰ)因为
所以的最小正周期为
(Ⅱ)因为
于是,当时,取得最大值2;
当取得最小值—1.
13已知函数;
(1)求的值;
(2)设求的值.
解:(1)
;
(2)
故
14设,满足,求函数在上的最大值和最小值.
解:
由
因此
当为增函数,
当为减函数,
所以
又因为
故上的最小值为
15已知函数的最大值是1,其图象经过点
(1)求的解析式;
(2)已知 且f(α)= ,求的值
17已知向量
(1)求的值;
知识的梳理
角的概念的推广
定义:一条射线由原来的位置,绕着它的端点按一定方向旋转到另一个位置,就形成了角,角分为正角,零角,负角。
象限角;
第一象限角:;
第二象限角:;
第三象限角:;
第四象限角:;
终边相同的角:一般地,所有与角终边相同的角连同角在内,可以表示为
二;弧度
1定义:用“弧度”作单位来度量角的制度,叫做弧度制。
2.角度与弧度的互化:
3,两个公式:(R为圆弧半径,为圆心角的弧度数)
扇形弧式:扇形面积公式:
三 三角函数的定义
1.定义:设是一个任意角,角的终边上任意一点,它与原点的距离为,那么角的正弦、余弦、正切分别是: 它们都是以角为自变量,以比值为函数值的函数
2 .三角函数在各象限内的符号口诀是:一全正;二正弦;三正切;四余弦;
3.同角三角函数的基本关系式
1)平法关系:
2)商数关系:
3)倒数关系:
四 诱导公式
组数 一 二 三 四 五 六
角
正弦
余弦
正切
口诀 函数名不变符号看象限 函数名改变符号看象限
特殊角的正弦,余弦,正切值如下:
五 正弦函数和余弦函数[定义域,值域,奇偶性,对称轴,单调性区间]
六由变换
七 和差倍角的三角函数
1.=_______________;= _______________
= ________________; ________________
_________________;________________
2.要辩证地看待和角与差角,根据需要,可以进行适当的变换: 等等;
3二倍角公式
= ________________=_______________ ;
4.在准确熟练地记住公式的基础上,要灵活运用公式解决问题:如公式的正用、逆用和变形用等.如T(α±β)可变形为:
5.函数,可以化为_______________;其中可由a,b的值唯一确定
八:三角函数的图象与性质
1.周期函数
(1)周期函数的定义
对于函数f(x),如果存在一个非零常数T,使得定义域内的每一个x值,都有.那么函数f(x) 就叫做周期函数。非零常数T叫做这个函数的周期.
(2)最小正周期
如果在周期函数f(x)的所有周期中存在一个最小正数,那么这个最小正数就叫做f(x)的最小正周期.
思考:如果函数y=f(x)的周期是T,那么函数y=f(ωx)的周期是多少?
例1如果为第一象限角,试问:是第几象限角?
例2已知一扇形的圆心角是,所在圆的半径是R.
若,求扇形的弧长及该弧所在的弓形的面积;
若扇形的周长是一定值,当为多少弧度时,该扇形有最大面积?
例3函数的值域是___________
例4求下列函数的定义域:
(1)
(2)
例5已知,求下列各式的值
(1)
(2)
变式 已知,求的值;
例6已知,求的值;
例7已知是关于的方程的两根;
求的值;
求的值;
例8已知函数
求的值
求的最大值和最小值;
变式1已知函数的定义域为,函数的最大值为1,最小值为,求和的值;
变式2 已知函数(其中的图像与x轴的交点中,相邻两个交点之间的距离为,且图像上一个最低点为.
求的解析式;
当时,求的值域;
例9将函数的图像上所有点向右平行移动个单位长度,在把所有各点的横坐标伸长到原来的2倍(纵坐标不变),所得图像的函数解析式是____________________
变式若函数的图像向右平移个单位长度后,与函数的图像重合,则的最小值为____________
例10已知函数)在时取得最大值4;
求的最小正周期;
求的解析式;
若,求;
变式已知函数;
求函数的最小正周期和图像的对称轴方程;
求函数在区间上的值域;
例11已知,求的值。
变式已知那么的值;
1. 的值是_____.
2.已知为第二象限角,且则
3.若则
4.已知 且α则
5若函数在区间上单调递增,在区间上单调递减,则
6设函数,将的图像向右平移个单位长度后,所得的图像与原图像重合,则的最小值等于________________
7已知函数,若,则x的取值范围为_______________
8设,则
9若,则的值等于_______________.6
10函数的最大值为_____________
11已知 则的值为__________
12已知函数。
(Ⅰ)求的最小正周期:
(Ⅱ)求在区间上的最大值和最小值。
解:(Ⅰ)因为
所以的最小正周期为
(Ⅱ)因为
于是,当时,取得最大值2;
当取得最小值—1.
13已知函数;
(1)求的值;
(2)设求的值.
解:(1)
;
(2)
故
14设,满足,求函数在上的最大值和最小值.
解:
由
因此
当为增函数,
当为减函数,
所以
又因为
故上的最小值为
15已知函数的最大值是1,其图象经过点
(1)求的解析式;
(2)已知 且f(α)= ,求的值
17已知向量
(1)求的值;
