21.2二次函数的图象性质 周测卷(含答案)
文档属性
| 名称 | 21.2二次函数的图象性质 周测卷(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 483.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-28 16:06:21 | ||
图片预览

文档简介
2021-2022学年初中数学-九年级
《二次函数的图像性质》周测卷
学校:______
姓名:______
班级:______
考号:______
单选题(5×8=40分)
1.抛物线y=x?-4x-4的开口方向、对称轴和顶点坐标分别为(
)
A.开口向上,对称轴是直线x=2,顶点是直线x=2,顶点是(2,8)
B.开口向上,对称轴是直线x=2,顶点是(2,-8)
C.开口向上,对称轴是直线x=-2,顶点是(2,-8)
D.开口向下,对称轴是直线x=2,顶点是(2,8)
2.若点A(-4,),B(-1,),C(1,)都是二次函数的图象上的点,则(
)
A.
B.
C.
D.
3.二次函数
的部分图象如图,图形过点(-1,0),对称轴为直线x=2,下列结论:①4a+b=0;②9a+3c>3b;③8a+7b+2c>0;④5a+c=0;⑤当x>-1时,y的值随着x值的增大而增大,其中正确的结论有(
)
A.2个
B.
3个
C.
4个
D.
5个
4.在同一直角坐标系中,一次函数y=-kx+1与二次函数的大致图象可以是(
)
5.如图是二次函数(其中a、b、c均为常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是直线x=1,对于下列说法:①;②③;④当-10;⑤,其中正确的是(
)
A.①②③
B.①②⑤
C.②③④
D.
③④⑤
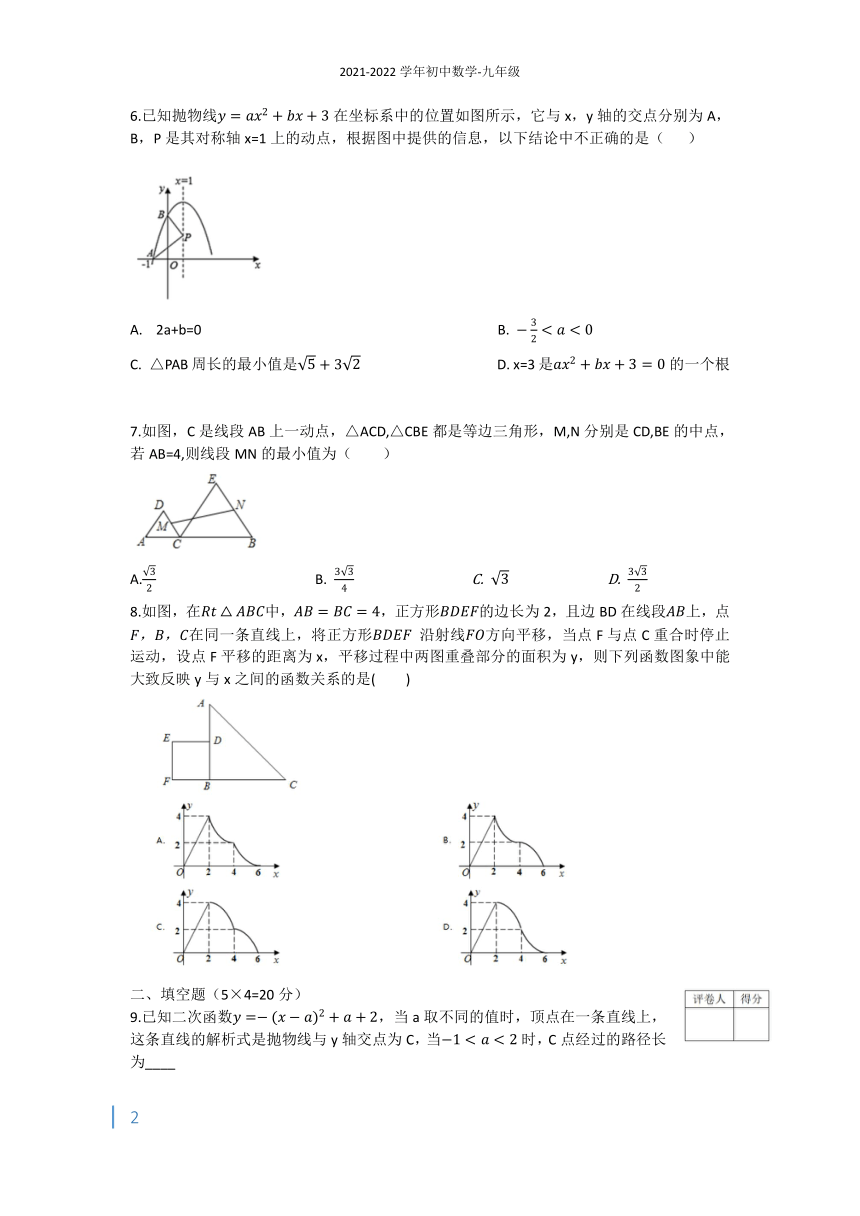
6.已知抛物线在坐标系中的位置如图所示,它与x,y轴的交点分别为A,B,P是其对称轴x=1上的动点,根据图中提供的信息,以下结论中不正确的是(
)
2a+b=0
B.
C.
△PAB周长的最小值是
D.
x=3是的一个根
7.如图,C是线段AB上一动点,△ACD,△CBE都是等边三角形,M,N分别是CD,BE的中点,若AB=4,则线段MN的最小值为(
)
A.
B.
C.
D.
8.如图,在中,,正方形的边长为2,且边BD在线段上,点在同一条直线上,将正方形
沿射线方向平移,当点F与点C重合时停止运动,设点F平移的距离为x,平移过程中两图重叠部分的面积为y,则下列函数图象中能大致反映y与x之间的函数关系的是(
)
填空题(5×4=20分)
9.已知二次函数,当a取不同的值时,顶点在一条直线上,这条直线的解析式是抛物线与y轴交点为C,当时,C点经过的路径长为____
10.二次函数的图象经过点A、B,顶点P的纵坐标是-2,则关于x的方程的解是_____
11.若二次函数在时的最大值为3,那么m的值是______.
12.如图,二次函数的图像与x轴交于两点,其中0<<1,下列四个结论①;②;③;④,正确的序号是______.
解答题(13题10分,14题14分,15题16分)
13.如图是二次函数的图象的一部分,根据图象回答下列问题:
(1)的解是______.
(2)确定的值;
(3)设抛物线的顶点是P与轴的另一个交点是B,试求的面积
14.如图,已知抛物线,点P是第一象限内抛物线上一个动点,作轴于点A,点B是第一象限内抛物线上的另一个点(点B在AP的右侧)
且,作轴于点C.
(1)当点P是抛物线的顶点时,求点B的坐标;
(2)当点B关于AP的对称点B恰好落在y轴上时,求OA的长.
15如图,二次函数的图象与x轴交于两点(点B在点C的左侧),一次函数的图象经过点B和二次函数图象上另一点A.其中
点A的坐标为
(1)求二次函数和一次函数的解析式;
(2)若抛物线上的点在第四象限内,过点P作轴的垂线PQ,交直线于点Q,求线段的最大值.
《二次函数的图像性质》周测卷答案解析
选择题
1
2
3
4
5
6
7
8
B
B
B
A
B
C
C
D
填空题
9.
①y=x+2
②
10.
x=1
11.
-4或
12.
①④
解答题
13.(1)-4和2
(2)
(3)
14.(1)
(2)
,点A坐标为
则OA=
15.
(1)一次函数解析式:
二次函数解析式:
(2)
【解析】(1)因为过点A(4,3),解得
再通过联立形成关于b,c的二元一次方程组;解得
(2)由点可知,将点Q的纵坐标减去点P的纵坐标,形成关于线段PQ的表达式,再利用配方法求最值;
当时取得最大值;
2
《二次函数的图像性质》周测卷
学校:______
姓名:______
班级:______
考号:______
单选题(5×8=40分)
1.抛物线y=x?-4x-4的开口方向、对称轴和顶点坐标分别为(
)
A.开口向上,对称轴是直线x=2,顶点是直线x=2,顶点是(2,8)
B.开口向上,对称轴是直线x=2,顶点是(2,-8)
C.开口向上,对称轴是直线x=-2,顶点是(2,-8)
D.开口向下,对称轴是直线x=2,顶点是(2,8)
2.若点A(-4,),B(-1,),C(1,)都是二次函数的图象上的点,则(
)
A.
B.
C.
D.
3.二次函数
的部分图象如图,图形过点(-1,0),对称轴为直线x=2,下列结论:①4a+b=0;②9a+3c>3b;③8a+7b+2c>0;④5a+c=0;⑤当x>-1时,y的值随着x值的增大而增大,其中正确的结论有(
)
A.2个
B.
3个
C.
4个
D.
5个
4.在同一直角坐标系中,一次函数y=-kx+1与二次函数的大致图象可以是(
)
5.如图是二次函数(其中a、b、c均为常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是直线x=1,对于下列说法:①;②③;④当-1
)
A.①②③
B.①②⑤
C.②③④
D.
③④⑤
6.已知抛物线在坐标系中的位置如图所示,它与x,y轴的交点分别为A,B,P是其对称轴x=1上的动点,根据图中提供的信息,以下结论中不正确的是(
)
2a+b=0
B.
C.
△PAB周长的最小值是
D.
x=3是的一个根
7.如图,C是线段AB上一动点,△ACD,△CBE都是等边三角形,M,N分别是CD,BE的中点,若AB=4,则线段MN的最小值为(
)
A.
B.
C.
D.
8.如图,在中,,正方形的边长为2,且边BD在线段上,点在同一条直线上,将正方形
沿射线方向平移,当点F与点C重合时停止运动,设点F平移的距离为x,平移过程中两图重叠部分的面积为y,则下列函数图象中能大致反映y与x之间的函数关系的是(
)
填空题(5×4=20分)
9.已知二次函数,当a取不同的值时,顶点在一条直线上,这条直线的解析式是抛物线与y轴交点为C,当时,C点经过的路径长为____
10.二次函数的图象经过点A、B,顶点P的纵坐标是-2,则关于x的方程的解是_____
11.若二次函数在时的最大值为3,那么m的值是______.
12.如图,二次函数的图像与x轴交于两点,其中0<<1,下列四个结论①;②;③;④,正确的序号是______.
解答题(13题10分,14题14分,15题16分)
13.如图是二次函数的图象的一部分,根据图象回答下列问题:
(1)的解是______.
(2)确定的值;
(3)设抛物线的顶点是P与轴的另一个交点是B,试求的面积
14.如图,已知抛物线,点P是第一象限内抛物线上一个动点,作轴于点A,点B是第一象限内抛物线上的另一个点(点B在AP的右侧)
且,作轴于点C.
(1)当点P是抛物线的顶点时,求点B的坐标;
(2)当点B关于AP的对称点B恰好落在y轴上时,求OA的长.
15如图,二次函数的图象与x轴交于两点(点B在点C的左侧),一次函数的图象经过点B和二次函数图象上另一点A.其中
点A的坐标为
(1)求二次函数和一次函数的解析式;
(2)若抛物线上的点在第四象限内,过点P作轴的垂线PQ,交直线于点Q,求线段的最大值.
《二次函数的图像性质》周测卷答案解析
选择题
1
2
3
4
5
6
7
8
B
B
B
A
B
C
C
D
填空题
9.
①y=x+2
②
10.
x=1
11.
-4或
12.
①④
解答题
13.(1)-4和2
(2)
(3)
14.(1)
(2)
,点A坐标为
则OA=
15.
(1)一次函数解析式:
二次函数解析式:
(2)
【解析】(1)因为过点A(4,3),解得
再通过联立形成关于b,c的二元一次方程组;解得
(2)由点可知,将点Q的纵坐标减去点P的纵坐标,形成关于线段PQ的表达式,再利用配方法求最值;
当时取得最大值;
2
