人教版数学七年级上册 4.3.1角课件(30张ppt)
文档属性
| 名称 | 人教版数学七年级上册 4.3.1角课件(30张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-28 10:42:55 | ||
图片预览








文档简介
(共30张PPT)
4.3.1
角
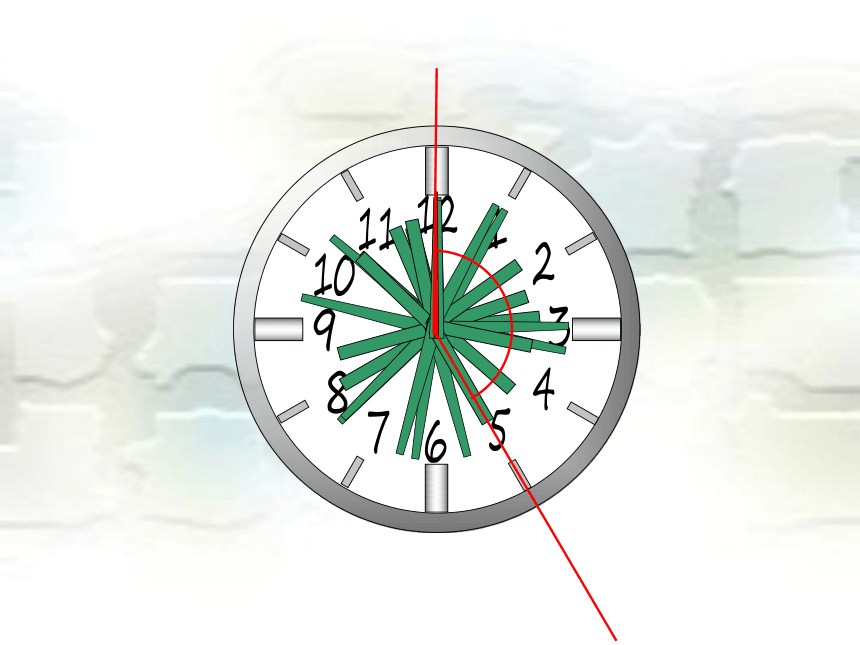
在生活有哪些实物
给我们角的形象呢?
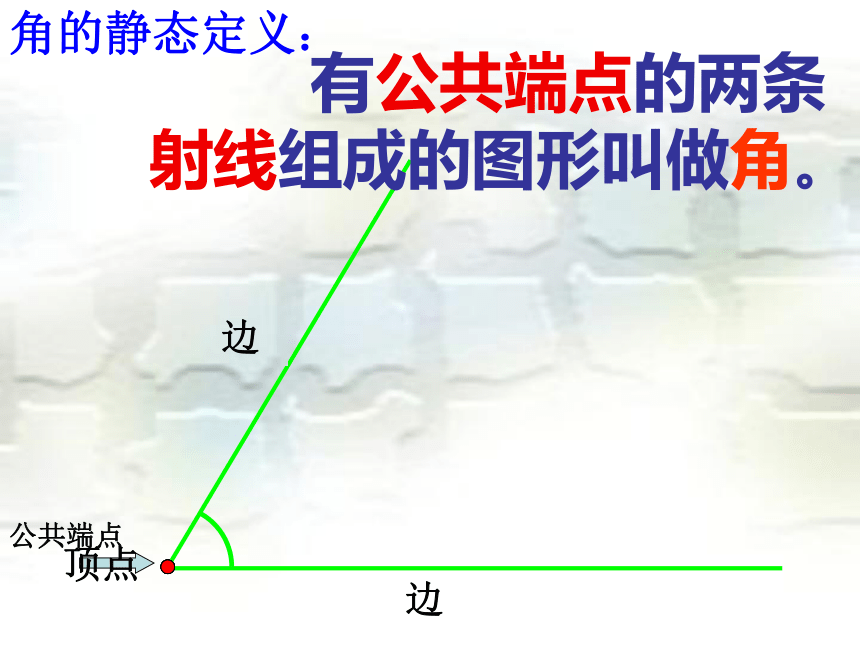
有公共端点的两条
射线组成的图形叫做角。
公共端点
顶点
射线
射线
边
边
角的静态定义:
角也可以看作由一条射线绕着它的端点旋转而形成的图形。
A
O
B
角的动态定义:
说明:
在不做特别说明的情况下,我们说的角都指不大于平角的角
当终边继续旋转到与始边成一条直线时,所成的角叫做平角;
当旋转到终边与始边再次重合时,所成的角叫做周角。
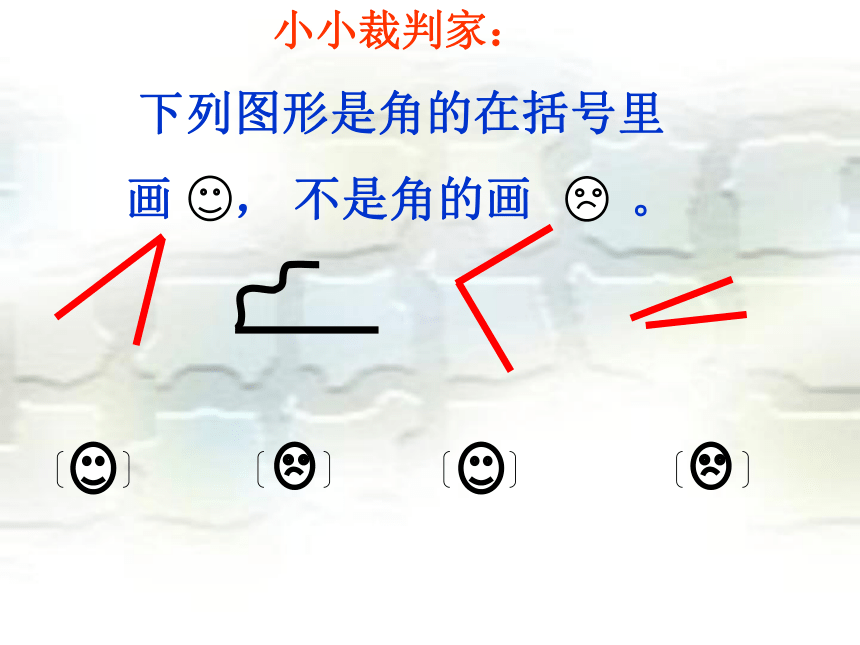
小小裁判家:
下列图形是角的在括号里
画
,
不是角的画 。
选择题:
下列语句正确的是(
)
A.两条直线相交,组成的图形叫做角;
B.两条有公共端点的线段组成的图形
叫角;
C.两条有公共点的射线组成的图形叫角;
D.
两条有公共端点的两条射线组成的图形叫角.
D
完成“练习二”
数一数,你能数出几个角?
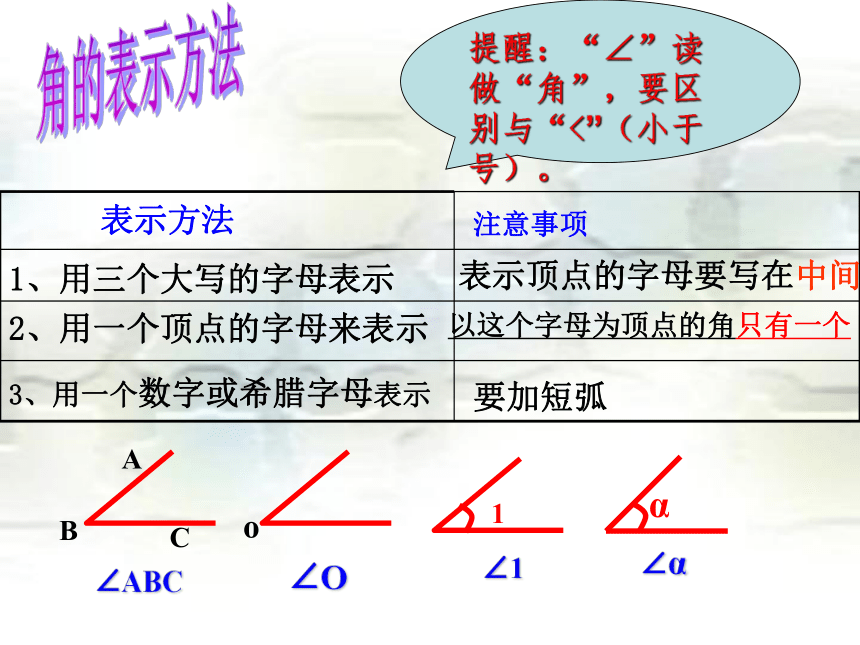
1、用三个大写的字母表示
表示方法
注意事项
表示顶点的字母要写在中间
C
A
B
∠ABC
2、用一个顶点的字母来表示
以这个字母为顶点的角只有一个
o
∠O
3、用一个数字或希腊字母表示
要加短弧
∠1
α
1
∠α
提醒:“∠”读做“角”,要区别与“<”(小于号)。
你会了吗?试一试!
把图中的角表示成下列形式:
①∠APO
②∠AOP
③∠OPC,
④∠O
⑤∠COP
⑥∠P。
其中正确的有
(把你认为正确的序号都填上。)
P
O
A
C
①
③
⑥
将图中的角用不同的方法表示出来,并填写下表
∠1
∠3
∠4
∠ACB
∠ABC
A
D
C
B
E
5
4
3
1
2
∠BCE
∠2
∠BAC
∠DAB
∠5
看一看图中有几个角,用适当的方法把它们表示出来.
A
B
C
D
∠ABD
,
∠DBC
,∠ABC
完成“练习三”
在此图中能用∠B表示角吗?
有人说:
∠1>
∠2,请问这种说法对吗?
1
2
角的大小
角的大小,我们习惯用角的两条边所夹的度数来表示,记做“°”,读做“度”
度量工具:量角器
1?
的角
1?
等分成60份
1'
1?
等分成60份
1"
1?
=60'
1
'
=60
"
度、分、秒是角的基本度量单位。
度分秒是60进制的
(1)1
°
=_____
′
(2)0.6
°=______′
(3)1′
=
______
″
(4)30′=____°
(5)3600″=___°
60
36
60
0.5
1
1?
=60′
1
'
=60
"
由上面的换算,你能总结出度分秒的换算规律?
度分秒的换算规律:
度
分
秒
×60
×60
÷60
÷60
×3600
÷3600
例:
(1)用度、分、秒表示1.12°
1.12°=
1
°+0.12
°
=1
°+0.12×60′
=1°+7
.2′
=
1°+7′+0.2
′
=1°+7′+0.2×60″
=1°+7′+12″
=1°7′12″
(2)
用度表示1?40'30″
1?40'30″=1°+40′+(30÷60)
′
=1°+
40′+0.5′
=1°+40.5′
=1°+(40.5÷60)
°
=1°+0.675°
=1.675°
1.用度、分、秒表示:
⑴0.75°= ′= ″;
⑵(
)°= ′= ″;
⑶16.24°= ° ′ ″.
4
15
45
2700
16
960
16
14
24
练习:
2、用度表示:
(1)1800″= ′=____°;
(2)50°7
′12
″=
50°
′=
°.
30
0.5
7.2
50.12
完成“练习四”
技巧1:
将度化为度、分、秒的形式的方法是:取整数后乘60再取整数,再乘60后取整数
技巧2:
将度、分、秒的形式化成度的形式的方法:a?b'c″=(a+b/60+c/3600)
?
完成“练习五”
角的定义(2种)
第一定义:有公共端点的两条射线组成的图形.
第二定义:由一条射线绕着它的端点旋转而
成的图形.
角的表示方法(3种)
度、分、秒的转换
表示方法
注意事项
1、用三个大写的字母表示
表示顶点的字母要写在中间
2、用一个顶点的字母来表示
以这个字母为顶点的角只有一个
3、用一个数字或希腊字母表示
要加短弧
1′=60″,1″=(
)′
1
60
1°=60′,1′=(
)°
1
60
学了这节课,你有哪些收获与体会……
小结
角的定义.
各种角(锐角、直角、。。。)
角的表示方法
角的度量单位的转换
问题探究:
3个角
?个角
?个角
(1)这些图中分别有几个角?
(2)你发现了什么规律?
(3)n条射线时,共有几个角?
??个角
3,6,10,15
B
F
K
P
4.3.1
角
在生活有哪些实物
给我们角的形象呢?
有公共端点的两条
射线组成的图形叫做角。
公共端点
顶点
射线
射线
边
边
角的静态定义:
角也可以看作由一条射线绕着它的端点旋转而形成的图形。
A
O
B
角的动态定义:
说明:
在不做特别说明的情况下,我们说的角都指不大于平角的角
当终边继续旋转到与始边成一条直线时,所成的角叫做平角;
当旋转到终边与始边再次重合时,所成的角叫做周角。
小小裁判家:
下列图形是角的在括号里
画
,
不是角的画 。
选择题:
下列语句正确的是(
)
A.两条直线相交,组成的图形叫做角;
B.两条有公共端点的线段组成的图形
叫角;
C.两条有公共点的射线组成的图形叫角;
D.
两条有公共端点的两条射线组成的图形叫角.
D
完成“练习二”
数一数,你能数出几个角?
1、用三个大写的字母表示
表示方法
注意事项
表示顶点的字母要写在中间
C
A
B
∠ABC
2、用一个顶点的字母来表示
以这个字母为顶点的角只有一个
o
∠O
3、用一个数字或希腊字母表示
要加短弧
∠1
α
1
∠α
提醒:“∠”读做“角”,要区别与“<”(小于号)。
你会了吗?试一试!
把图中的角表示成下列形式:
①∠APO
②∠AOP
③∠OPC,
④∠O
⑤∠COP
⑥∠P。
其中正确的有
(把你认为正确的序号都填上。)
P
O
A
C
①
③
⑥
将图中的角用不同的方法表示出来,并填写下表
∠1
∠3
∠4
∠ACB
∠ABC
A
D
C
B
E
5
4
3
1
2
∠BCE
∠2
∠BAC
∠DAB
∠5
看一看图中有几个角,用适当的方法把它们表示出来.
A
B
C
D
∠ABD
,
∠DBC
,∠ABC
完成“练习三”
在此图中能用∠B表示角吗?
有人说:
∠1>
∠2,请问这种说法对吗?
1
2
角的大小
角的大小,我们习惯用角的两条边所夹的度数来表示,记做“°”,读做“度”
度量工具:量角器
1?
的角
1?
等分成60份
1'
1?
等分成60份
1"
1?
=60'
1
'
=60
"
度、分、秒是角的基本度量单位。
度分秒是60进制的
(1)1
°
=_____
′
(2)0.6
°=______′
(3)1′
=
______
″
(4)30′=____°
(5)3600″=___°
60
36
60
0.5
1
1?
=60′
1
'
=60
"
由上面的换算,你能总结出度分秒的换算规律?
度分秒的换算规律:
度
分
秒
×60
×60
÷60
÷60
×3600
÷3600
例:
(1)用度、分、秒表示1.12°
1.12°=
1
°+0.12
°
=1
°+0.12×60′
=1°+7
.2′
=
1°+7′+0.2
′
=1°+7′+0.2×60″
=1°+7′+12″
=1°7′12″
(2)
用度表示1?40'30″
1?40'30″=1°+40′+(30÷60)
′
=1°+
40′+0.5′
=1°+40.5′
=1°+(40.5÷60)
°
=1°+0.675°
=1.675°
1.用度、分、秒表示:
⑴0.75°= ′= ″;
⑵(
)°= ′= ″;
⑶16.24°= ° ′ ″.
4
15
45
2700
16
960
16
14
24
练习:
2、用度表示:
(1)1800″= ′=____°;
(2)50°7
′12
″=
50°
′=
°.
30
0.5
7.2
50.12
完成“练习四”
技巧1:
将度化为度、分、秒的形式的方法是:取整数后乘60再取整数,再乘60后取整数
技巧2:
将度、分、秒的形式化成度的形式的方法:a?b'c″=(a+b/60+c/3600)
?
完成“练习五”
角的定义(2种)
第一定义:有公共端点的两条射线组成的图形.
第二定义:由一条射线绕着它的端点旋转而
成的图形.
角的表示方法(3种)
度、分、秒的转换
表示方法
注意事项
1、用三个大写的字母表示
表示顶点的字母要写在中间
2、用一个顶点的字母来表示
以这个字母为顶点的角只有一个
3、用一个数字或希腊字母表示
要加短弧
1′=60″,1″=(
)′
1
60
1°=60′,1′=(
)°
1
60
学了这节课,你有哪些收获与体会……
小结
角的定义.
各种角(锐角、直角、。。。)
角的表示方法
角的度量单位的转换
问题探究:
3个角
?个角
?个角
(1)这些图中分别有几个角?
(2)你发现了什么规律?
(3)n条射线时,共有几个角?
??个角
3,6,10,15
B
F
K
P
