《同角三角函数的基本关系》

(共13张PPT)
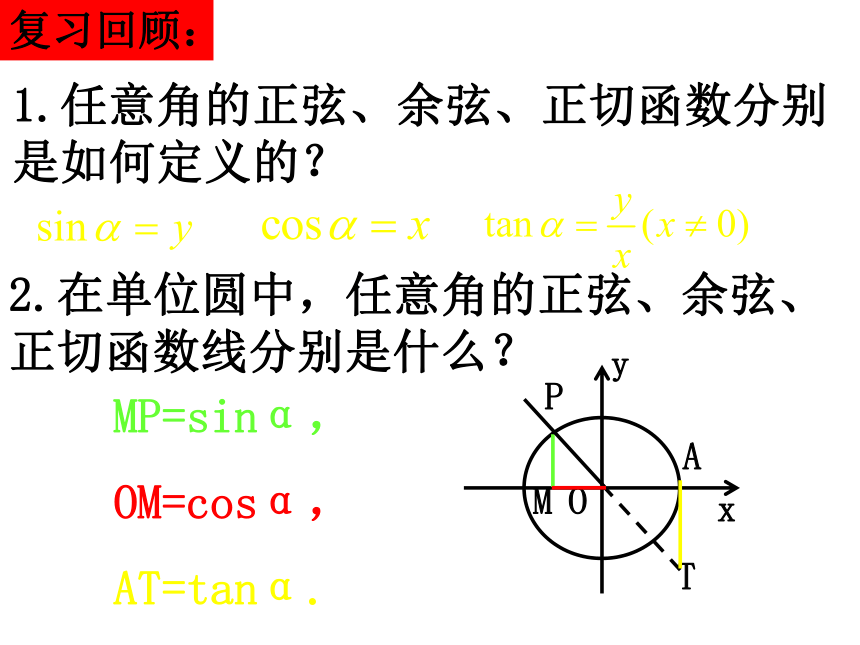
复习回顾：
1.任意角的正弦、余弦、正切函数分别是如何定义的？
2.在单位圆中，任意角的正弦、余弦、正切函数线分别是什么？
MP=sinα，
OM=cosα，
AT=tanα.
P
O
x
y
M
A
T
3.对于一个任意角α，sinα，cosα，tanα是三个不同的三角函数，从联系的观点来看，三者之间应存在一定的内在联系，我们希望找出这种同角三角函数之间的基本关系，实现正弦、余弦、正切函数的互相转化，为进一步解决三角恒等变形问题提供理论依据．
知识探究（一）：基本关系
思考1：如图，设α是一个任意角，它的终边与单位圆交于点P，那么，正弦线MP和余弦线OM的长度有什么内在联系？由此能得到什么结论？
P
O
x
y
M
1
思考2：上述关系反映了角α的正弦和余弦之间的内在联系，根据等式的特点，将它称为平方关系.那么当角α的终边在坐标轴上时，上述关系成立吗？
O
x
y
P
P
思考3：设角α的终边与单位圆交于点 P（x，y），根据三角函数定义，有
， ， ， 由此可得sinα，cosα，tanα满足什么关系？
思考4：上述关系称为商数关系，那么商数关系成立的条件是多么？
同一个角的正弦、余弦的平方和等于1，商等于这个角的正切.
思考5：平方关系和商数关系是反映同一个角的三角函数之间的两个基本关系，它们都是恒等式，如何用文字语言描述这两个关系？
知识探究（二）：基本变形
思考1：对于平方关系 可作哪些变形？
思考2：对于商数关系 可作哪些变形？
思考3：结合平方关系和商数关系，可得到哪些新的恒等式？
思考4：若已知sinα的值，如何求cosα和tanα的值？
思考5：若已知tanα的值，如何求sinα和cosα的值？
理论迁移
例1 求证：
例2 已知 ,求 ， 的值.
例3 已知tanα=2，求下列各式的值.
（1） ；（2）
例4 已知 ，
求 的值.
小结作业
1.同角三角函数的两个基本关系是对同一个角而言的，由此可以派生出许多变形公式，应用中具有灵活、多变的特点.
2.利用平方关系求值时往往要进行开方运算，因此要根据角所在的象限确定三角函数值符号，必要时应就角所在象限进行分类讨论．
3.化简、求值、证明，是三角变换的三个基本问题，具有一定的技巧性，需要加强训练，不断总结、提高.