函数的单调性

(共47张PPT)
理解函数的单调性、最大值、最小值及其几何意义
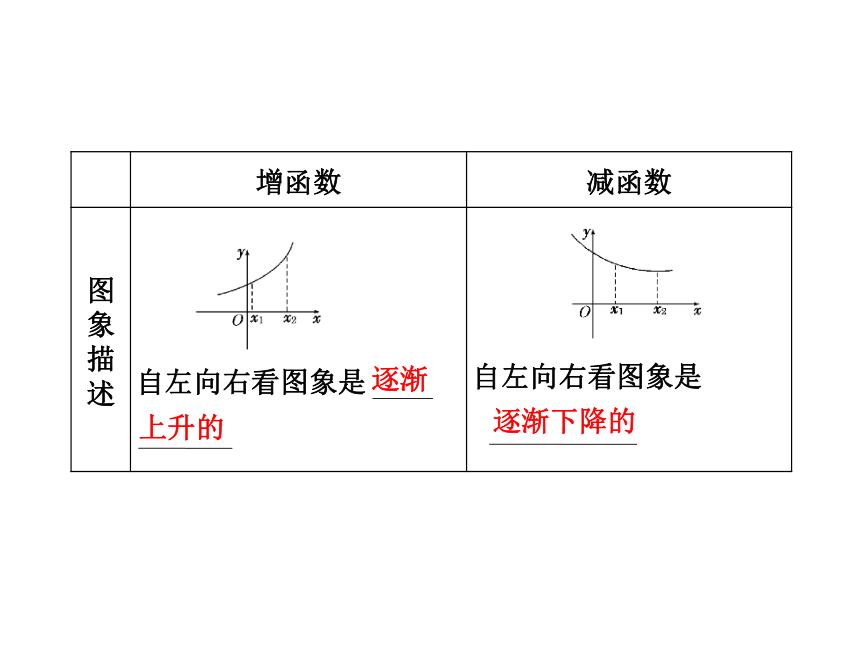
增函数 减函数
定　义 一般地，设函数f(x)的定义域为I.如果对于定义域I内某个区间D上的任意两个自变量x1，x2，
当x1＜x2时，都有 ，那么就说函数f(x)在区间D上是增函数 当x1＜x2时，都有 ，那么就说函数f(x)在区间D上是减函数
f(x1)＜f(x2)
f(x1)＞f(x2)
1.单调函数的定义
增函数 减函数
图象描述
自左向右看图象是
自左向右看图象是
上升的
逐渐
逐渐下降的
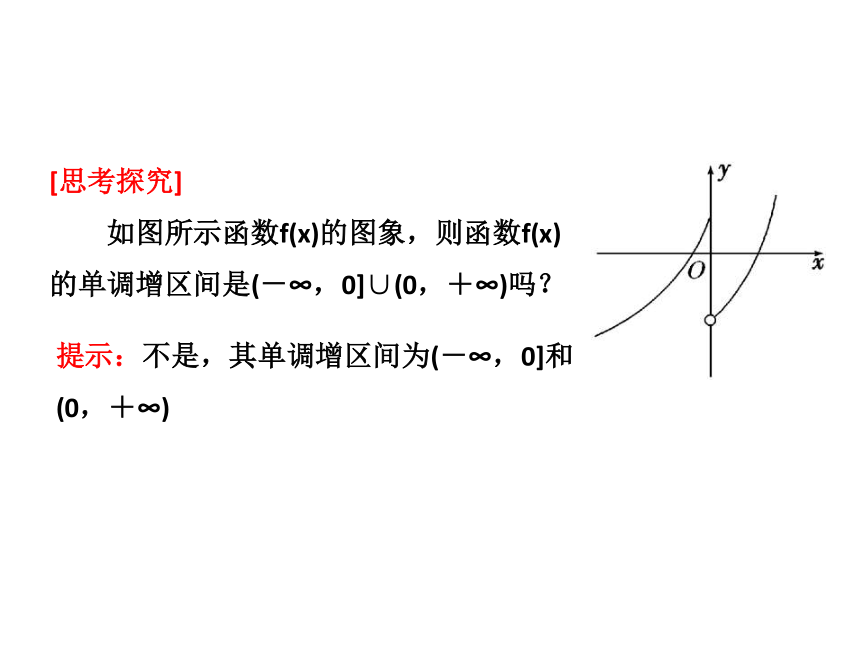
[思考探究]
　　如图所示函数f(x)的图象，则函数f(x) 的单调增区间是(－∞，0]∪(0，＋∞)吗？
提示：不是，其单调增区间为(－∞，0]和
(0，＋∞)
2.单调区间的定义
若函数y＝f(x)在区间D上是 或 ，则称函数
f(x)在这一区间上具有(严格的)单调性， 叫做y＝f(x)
的单调区间.
增函数
减函数
区间D
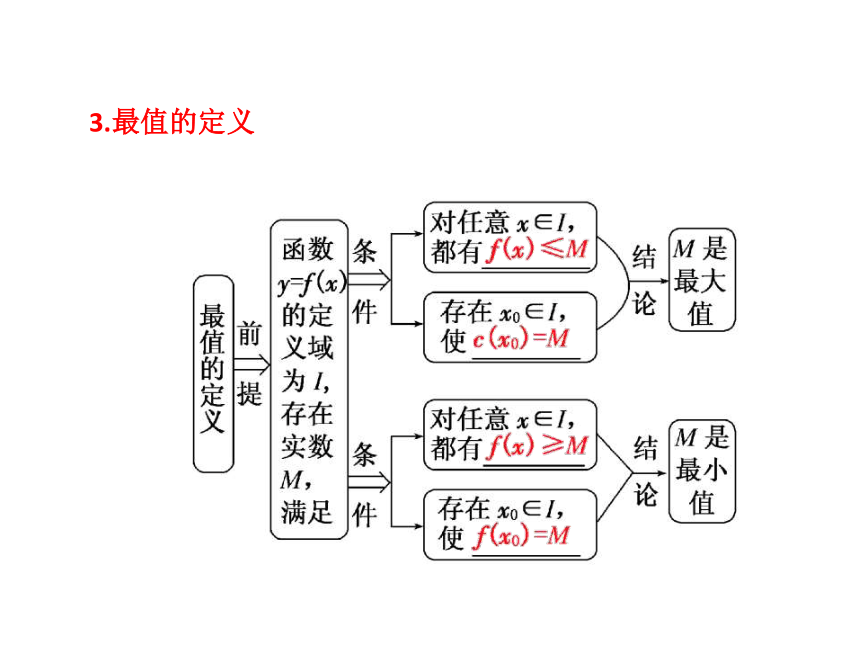
3.最值的定义
1.下列函数中，在区间(0,2)上为增函数的是 (　　)
A.y＝－x＋1　　　　　　B.y＝
C.y＝x2－4x＋5 D.y＝
解析：∵函数y＝ 的单调增区间为[0，＋∞)，
∴函数y＝ 在(0,2)上为增函数.
答案：B
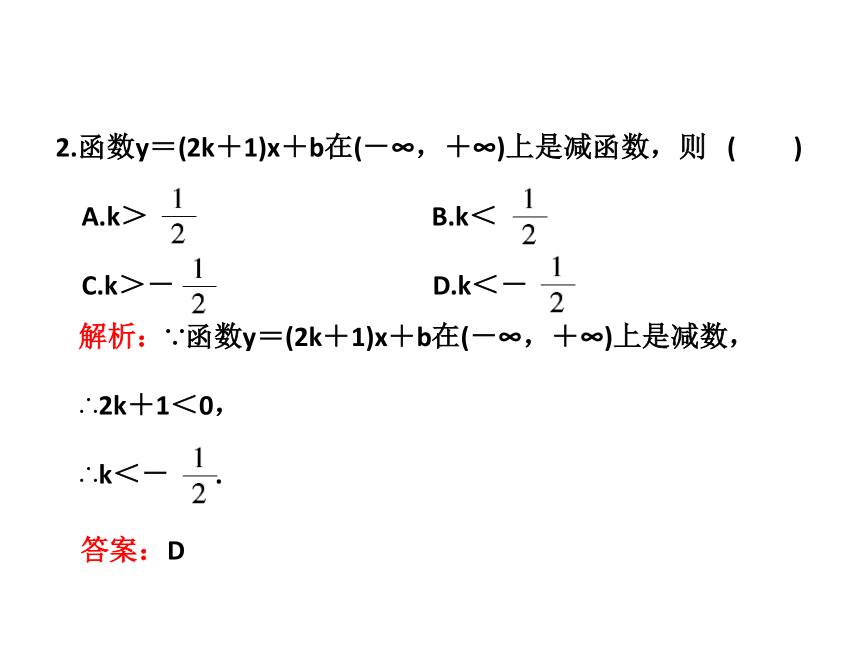
2.函数y＝(2k＋1)x＋b在(－∞，＋∞)上是减函数，则 (　　)
A.k＞ B.k＜
C.k＞－ D.k＜－
解析：∵函数y＝(2k＋1)x＋b在(－∞，＋∞)上是减数，
∴2k＋1＜0，
∴k＜－ .
答案：D
3.若函数y＝ax与y＝－ (0，＋∞)上都是减函数，则y＝ax2
＋bx在(0，＋∞)上是 (　　)
A.增函数 B.减函数
C.先增后减 D.先减后增
解析：∵函数y＝ax与y＝－ 在(0，＋∞)上都是减函数，
∴a＜0，b＜0，
∴函数y＝ax2＋bx的图象的对称轴为x＝－ ＜0，
∴函数y＝ax2＋bx在(0，＋∞)是减函数.
答案：B
4.如果函数f(x)在[a，b]上是增函数，对于任意的x1、x2∈[a，
b](x1≠x2)，下列结论中正确的有　　　　.
① ＞0；
②(x1－x2)[f(x1)－f(x2)]＞0；
③f(a)＜f(x1)＜f(x2)＜f(b)；
④ ＞0.
解析：∵f(x)在[a，b]上为增函数.
∴x1－x2与f(x1)－f(x2)的符号相同.
∴①②④均正确.
又∵不知道x1，x2的大小，∴无法比较f(x1)与f(x2)的大小，故③错误.
答案：①②④
5.已知函数f(x)＝2ax2＋4(a－3)x＋5在区间(－∞，3)上是减
函数，则a的取值范围是　　　　.
解析：①当a＝0时，f(x)＝－12x＋5，在(－∞，3)上为减
函数；②当a>0时，要使f(x)＝2ax2＋4(a－3)x＋5在区间
(－∞，3)上是减函数，则对称轴x＝ 必在x＝3的右
边，即 ≥3，故0间(－∞，3)上恒为减函数.
综合知：a的取值范围是[0， ].
答案：[0， ]
1.用定义证明函数单调性的一般步骤
(1)取值：即设x1，x2是该区间内的任意两个值，且x1＜x2.
(2)作差：即f(x2)－f(x1)(或f(x1)－f(x2))，并通过通分、配方、
因式分解等方法，向有利于判断差的符号的方向变形.
(3)定号：根据给定的区间和x2－x1的符号，确定差f(x2)－
f(x1)(或f(x1)－f(x2))的符号.当符号不确定时，可以进行分
类讨论.
(4)判断：根据定义得出结论.
2.(1)若f(x)与g(x)在定义域内均是增函数(减函数)，那么f(x)＋
g(x)在其公共定义域内是增函数(减函数).
(2)复合函数的单调性判断，要注意掌握“同则增，异则减”.
讨论函数f(x)＝ (a＞0)的单调性.
[思路点拨]
[课堂笔记]　∵f(x)＝ ，
∴函数的定义域为{x|x∈R且x≠1}.
法一：(定义法)任取x1，x2∈R，且x1，x2均不为1，x1＜x2，
则f(x1)－f(x2)＝(a＋ )－(a＋ )
＝
＝ .
①设x1＜x2＜1，x1－1＜0，x2－1＜0，x2－x1＞0，a＞0，
∴f(x1)－f(x2)＞0，即f(x1)＞f(x2).
②设1＜x1＜x2，x2－1＞0，x1－1＞0，x2－x1＞0，a＞0，
∴f(x1)－f(x2)＞0，即f(x1)＞f(x2).
∴函数f(x)在(－∞，1)和(1，＋∞)上均为减函数.
法二：(导数法)∵f′(x)＝ ，
又∵a＞0，
∴f′(x)＜0在(－∞，1)∪(1，＋∞)上恒成立，即函数f(x)在
(－∞，1)和(1，＋∞)上均为减函数.
法三：(图象法)由f(x)＝a＋ 可知其图象对称中心是(1，a)，x＝1，y＝a是它的两条渐近线，故其图象如图所示，
∴f(x)在(－∞，1)和(1，＋∞)上均为减函数.
讨论函数f(x)＝ (a≠0，－1＜x＜1)的单调性.
解：设－1＜x1＜x2＜1，
则f(x1)－f(x2)＝
＝ .
∵－1＜x1＜x2＜1，
∴|x1|＜1，|x2|＜1，x2－x1＞0，
－1＜0， －1＜0，|x1x2|＜1，
即－1＜x1x2＜1，∴x1x2＋1＞0.
∴ ＞0.
因此，当a＞0时，f(x1)－f(x2)＞0.
即f(x1)＞f(x2)，此时函数f(x)在(－1,1)上为减函数；
当a＜0时，f(x1)－f(x2)＜0，
即f(x1)＜f(x2)，此时函数f(x)在(－1,1)上为增函数.
1.求函数的单调区间
(1)利用已知函数的单调性.
(2)定义法：先求定义域，再利用单调性定义.
(3)图象法：如果f(x)是以图象给出的，或者f(x)的图象易作出
可直接由图象的直观性写出它的单调区间.
(4)导数法：利用导函数取值的正负确定原函数的单调区间.
2.求复合函数y＝f[g(x)]的单调区间的步骤
(1)确定定义域.
(2)将复合函数分解成基本初等函数：y＝f(u)，u＝g(x).
(3)分别确定这两个函数的单调区间.
(4)若这两个函数同增或同减，则y＝f[g(x)]为增函数；
若一增一减，则y＝f[g(x)]为减函数，即“同增异减”.
求下列函数的单调区间
(1)f(x)＝x2－4|x|＋3；
(2)f(x)＝ .
[思路点拨]
[课堂笔记]　(1)f(x)＝x2－4|x|＋3＝ 于是可得函数f(x)＝x2－4|x|＋3的图象，如图所示.
由图可知，函数的增区间为[－2,0)，(2，＋∞)，
减区间为(－∞，－2)，[0,2).
(2)∵y＝ ，
∴该函数的定义域为(－∞，－1]∪[1，＋∞).
又∵y＝ 可看作是由
y＝ 与u＝x2－1两个函数复合而成的，
且y＝ 在u∈[0，＋∞)上为增函数，
而u＝x2－1在(－∞，－1]上为减函数且u≥0，
在[1，＋∞)上为增函数且u≥0.
∴当x∈(－∞，－1]时，y＝ 为减函数，
当x∈[1，＋∞)时，y＝ 为增函数.
对于抽象函数的单调性的判断仍然要紧扣单调性的定义，结合题目中所给性质和相应的条件，对任意x1，x2在所给区间内比较f(x1)－f(x2)与0的大小，或 与1的大小.有时根据需要，需作适当的变形：如x1＝x2· 或x1＝x2＋x1－x2等.
已知函数f(x)对于任意x，y∈R，总有f(x)＋f(y)＝f(x＋y)，且当x＞0时，f(x)＜0，f(1)＝－ .
(1)求证：f(x)在R 上是减函数；
(2)求f(x)在[－3,3]上的最大值和最小值.
[思路点拨]
[课堂笔记]　(1)法一：∵函数f(x)对于任意x，y∈R总有f(x)＋f(y)＝f(x＋y)，
∴令x＝y＝0，得f(0)＝0.
再令y＝－x，得f(－x)＝－f(x).
在R上任取x1＞x2，则x1－x2＞0，
f(x1)－f(x2)＝f(x1)＋f(－x2)＝f(x1－x2).
又∵x＞0时，f(x)＜0，而x1－x2＞0，∴f(x1－x2)＜0，
即f(x1)＜f(x2).
因此f(x)在R上是减函数.
法二：设x1＞x2，
则f(x1)－f(x2)
＝f(x1－x2＋x2)－f(x2)
＝f(x1－x2)＋f(x2)－f(x2)
＝f(x1－x2).
又∵x＞0时，f(x)＜0.而x1－x2＞0，∴f(x1－x2)＜0，
即f(x1)＜f(x2)，
∴f(x)在R上为减函数.
(2)∵f(x)在R上是减函数，∴f(x)在[－3,3]上也是减函数，∴f(x)在[－3,3]上的最大值和最小值分别为f(－3)
与f(3).
而f(3)＝3f(1)＝－2，f(－3)＝－f(3)＝2.
∴f(x)在[－3,3]上的最大值为2，最小值为－2.
　 高考对函数单调性的考查方式灵活，既有函数单调性的判定、单调区间的求法，又有利用函数单调性解不等式、比较大小、求最值等.而抽象函数的单调性问题脱离了特殊的函数模型的实际背景，
由一个抽象的代数公式诠释一个具有深远意义的函数性质，从近几年高考看，抽象函数与函数的单调性相结合求参数的取值范围或求自变量x的取值范围成为高考命题的一个新考向.
　[考题印证]
(2009·辽宁高考)已知偶函数f(x)在区间[0，＋∞)单调增加，则满足f(2x－1)A.( ， )　　　　　 B.[ ， )
C.( ， ) D.[ ， )
【解析】　f(x)是偶函数，其图象关于y轴对称，又f(x)在[0，＋∞)上递增，
∴f(2x－1)【答案】　A
　 [自主体验]
函数f(x)在R上是增函数，且对任意a，b∈R，都有f(a＋b)＝f(a)＋f(b)－1，若f(4)＝5，则不等式f(3m2－m－2)＜3的解集为　　　　.
答案：(－1， )
解析：∵f(4)＝f(2＋2)＝f(2)＋f(2)－1＝5，
∴f(2)＝3，
∴原不等式可化为f(3m2－m－2)∵f(x)是R上的增函数，
∴3m2－m－2<2，解得－1故解集为(－1， ).
1.(2010·大连模拟)下列函数在(0,1)上是减函数的是 (　　)
A.y＝log0.5(1－x) B.y＝x0.5
C.y＝0.51－x D.y＝ (1－x2)
解析：y＝log0.5(1－x)在(0,1)上为增函数；
y＝x0.5在(0,1)上是增函数；
y＝0.51－x在(0,1)上为增函数；
函数y＝ (1－x2)在(－∞，0)上为增函数，在(0，＋∞)
上为减函数，
∴函数y＝ (1－x2)在(0,1)上是减函数.
答案：D
2.已知f(x)为R上的减函数，则满足f( )＞f(1)的实数x的取值
范围是 (　　)
A.(－∞，1) B.(1，＋∞)
C.(－∞，0)∪(0,1) D.(－∞，0)∪(1，＋∞)
解析：依题意得 ＜1，即 ＞0，所以x的取值范围是x＞1或x＜0，选D.
答案：D
3.(2010·德州模拟)已知f(x)＝ 是
(－∞，＋∞)上的增函数，那么a的取值范围是(　　)
A.(1，＋∞) B.(－∞，3)
C.[ , 3) D.(1,3)
解析：(1)由于x≥1时，f(x)＝logax单调递增，故a＞1；
(2)x＜1时，f(x)＝(3－a)x－4a单调递增，故3－a＞0，
a＜3；要同时满足(1)(2)两个条件，则1＜a＜3，此时
(3－a)x－4a＜0(x＜1)，又logax≥0(x≥1)，满足题意.
答案：D
4. y ＝ 的递减区间是　　　　，y＝ 的递减
区间是　　　　.
解析：y＝ ＝ ＝－1＋ ,
∴y＝ 的递减区间是(－1，＋∞)和(－∞，－1).
要使函数y＝ 有意义，则 ≥0，且1＋x≠0，
∴－1＜x≤1
∴y＝ 的递减区间为(－1,1].
答案：(－1，＋∞)和(－∞，－1)　(－1,1]
5.若在区间[ ,2]上，函数f(x)＝x2＋px＋q与g(x)＝x＋
在同一点取得相同的最小值，则f(x)在该区间上的
最大值是　　　.
解析：对于g(x)＝x＋ 在x＝1时，g(x)取最小值为2，
则f(x)在x＝1时取最小值2，
∴－ ＝1，f(1)＝1＋p＋q＝2.
∴p＝－2，q＝3.
∴f(x)＝x2－2x＋3，
∴f(x)在该区间上的最大值为3.
答案：3
6.已知函数f(x)＝ (a>0，x>0)，
(1)求证：f(x)在(0，＋∞)上是单调递增函数；
(2)若f(x)在 上的值域是 ，求a的值.
解：(1)证明：设x2>x1>0，则x2－x1>0，x1x2>0，
∵f(x2)－f(x1)＝
＝ ＝ >0，
∴f(x2)>f(x1)，∴f(x)在(0，＋∞)上是单调递增的.
(2)∵f(x)在 上的值域是 ，
又f(x)在 上单调递增，
∴f ＝ ，f(2)＝2.∴易得a＝ .