《集合》复习课件

(共13张PPT)
新干二中 廖海林
1
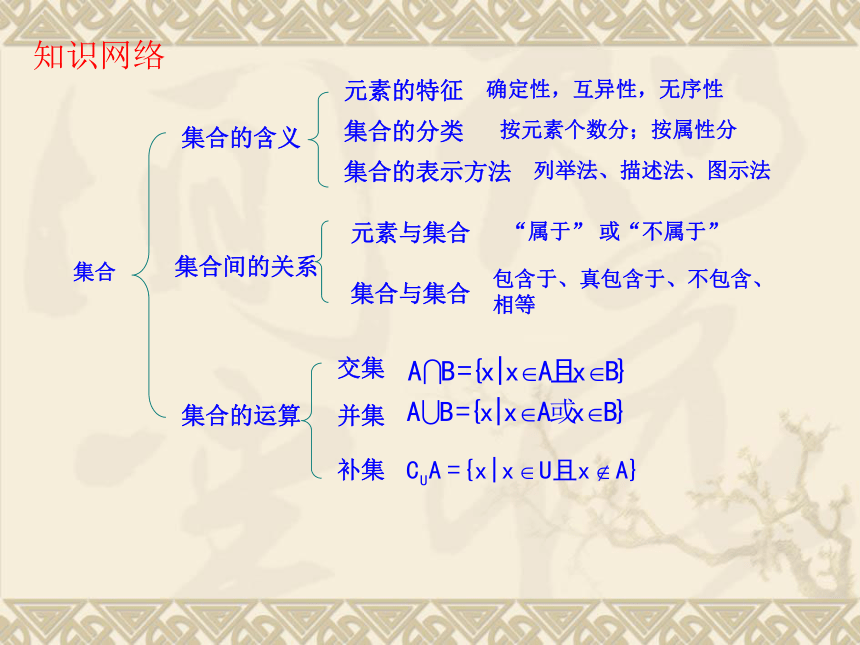
知识网络
集合
集合的含义
元素的特征
集合的分类
集合的表示方法
集合间的关系
元素与集合
集合与集合
集合的运算
交集
并集
补集
确定性，互异性，无序性
列举法、描述法、图示法
“属于” 或“不属于”
包含于、真包含于、不包含、相等
按元素个数分；按属性分
复习方向1:集合概念、分类、表示方法、运算
B={y|y=x2+1},
例:已知A={x|y=x2+1},
C={(x,y)|y=x2+1},
E={(x,y)|y=x+1},
D={y=x2+1},
(1) A、B、C、D、E这5个集合各是何种集合？
（2）计算A∩B， A∩C ，C∩E.
它们是用何种方法表示的
特别提示：解答集合问题，必须准确理解集合 的有关概念， 对于用描述法给出的集合 {ｘ｜ｘ∈P},要紧紧抓住竖线前面的代表x以及它所具有的 性质P.
例2:x,y是实数,集合
A
A.1 B.-1 C.0 D.+1或-1
例题2:已知集合A={x|x2+4x=0}
B={x|x2+2(a+1)x+a2_1=0}
(1).若集合B中只有一个元素,求实数a的值
(2).若集合B中至少有一个元素,求实数a的取值范围；
(3).若集合B中至多有一个元素,求实数a的取值范围；
(4).若B A, 求实数a的取值范围；
(5).若A∪B=B求实数a的值；
(6).若A∩B≠Ф求实数a的值；
复习方向2：集合关系,求参数值及范围
（1）空集是任何集合的子集；是任何非空集合的真子集
（2）任何集合都是它本身的子集
例题3:已知集合A={x|m-1B={x|0≤ x≤ 1}
(1).若A∩B ＝B， 求实数m的取值范围；
(4).若CR A CRB, 求实数m的取值范围；
(3).若B A, 求实数m的取值范围；
(5).若A∪B ＝B , 求实数m的取值范围；
(7).若A∩B ＝Ф ，求实数m的取值范围；
(6).若B CR A, 求实数m的取值范围；
R是全集,
(8).若A∩B≠Ф, 求实数m的取值范围；
(2).若A∪B ＝A， 求实数m的取值范围；
0
1
0
1
x
1
0
x
0
1
m-1
x
2m+1
2m+1
m-1
m-1
2m+1
1
m-1
2m+1
x
0
1
0
复习方向3；集合实际应
例：向50名学生调查对A、B两事件的态度，有如下结果：赞成A的人数是30，其余的不赞成，赞成B的人数是33，其余的不赞成；另外，对A、B都不赞成的学生比对A、B都赞成的学生数的三分之一多1人.问对A、B都赞成的学生和都不赞成的学生各多少人？
分析：
画出韦恩图，形象地表示出各数量关系的联系
8
小结：
1.基本概念的理解与掌握
2. 数形结合思想：解答某些集合问题,一般借助数轴和文氏图求解，以“形”助“数”,形象、直观,方便快捷。
3. 等价转化思想：解答集合问题时，有时需要对给定的条件进行转化,只有通过转化，给定的条件才能得以有效利用。如将
4. 分类讨论思想：根据解题的实际需要，有时需要对解题过程的某一环节分类讨论。分类讨论要注意“起点”的寻找和“层次”的划分，做到“起点”讨论合理自然， “层次”划分明确清晰。分类讨论的原则是“既不重复，也不遗漏”。
3.已知集合A={x|－2≤x≤4},B={x|x＞a}
①若A∩B≠φ,求实数a的取值范围;
②若A∩B≠A,求实数a的取值范围．
2.已知集合A={x |－2≤x≤4}, B={x|x＞a}
①若A∩B≠φ,求实数a的取值范围;
②若A∩B≠A,求实数a的取值范围．
1.设A={x,x2,xy},B={1,x,y},且A=B，求实数x,y的值．
作业