指数函数(2)

(共21张PPT)
指数函数(2)
指数函数的定义：
函数
叫做指数函数，其中x是自变量，函数定义域是R。
复习上节内容
探究1：为什么要规定a>0,且a
1呢？
①若a=0，则当x>0时，
=0；
0时，
无意义.
当x
②若a<0，则对于x的某些数值，可使
无意义.
如
，这时对于x=
，x=
……等等，在实数范围内函数值不存在.
③若a=1，则对于任何x
R，
=1，是一个常量，没有研究的必要性.
为了避免上述各种情况，所以规定a>0且a 1。
在规定以后，对于任何x
R，
都有意义，且
>0. 因此指数函数的定义域是R，值域是(0,+∞).
复习上节内容
探究2：函数
是指数函数吗？
指数函数的解析式y=
中，
的系数是1.
有些函数貌似指数函数，实际上却不是，如
(a>0且a
1，k
Z)；
有些函数看起来不像指数函数，实际上却是，如
因为它可以化为
复习上节内容
指数函数的图象和性质：
在同一坐标系中分别作出如下函数的图像：
列表如下：
x … -3 -2 -1 -0.5 0 0.5 1 2 3 …
… 0.13 0.25 0.5 0.71 1 1.4 2 4 8 …
… 8 4 2 1.4 1 0.71 0.5 0.25 0.13 …
复习上节内容
x … -2.5 -2 -1 -0.5 0 0.5 1 2 2.5 …
… 0.06 0.1 0.3 0.6 1 1.7 3 9 15.6 …
… 15.6 9 3 1.7 1 0.6 0.3 0.1 0.06 …
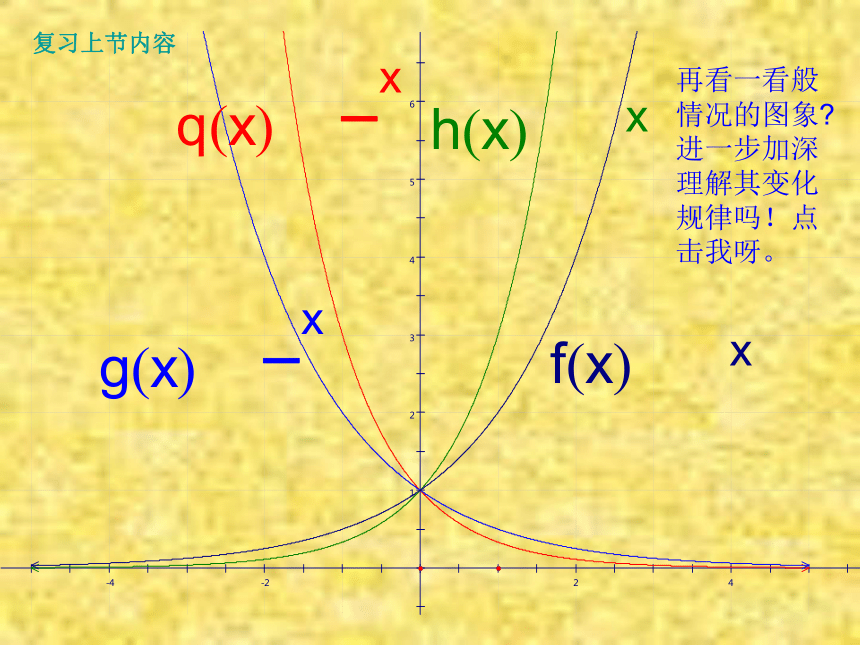
再看一看般情况的图象 进一步加深理解其变化规律吗！点击我呀。
复习上节内容
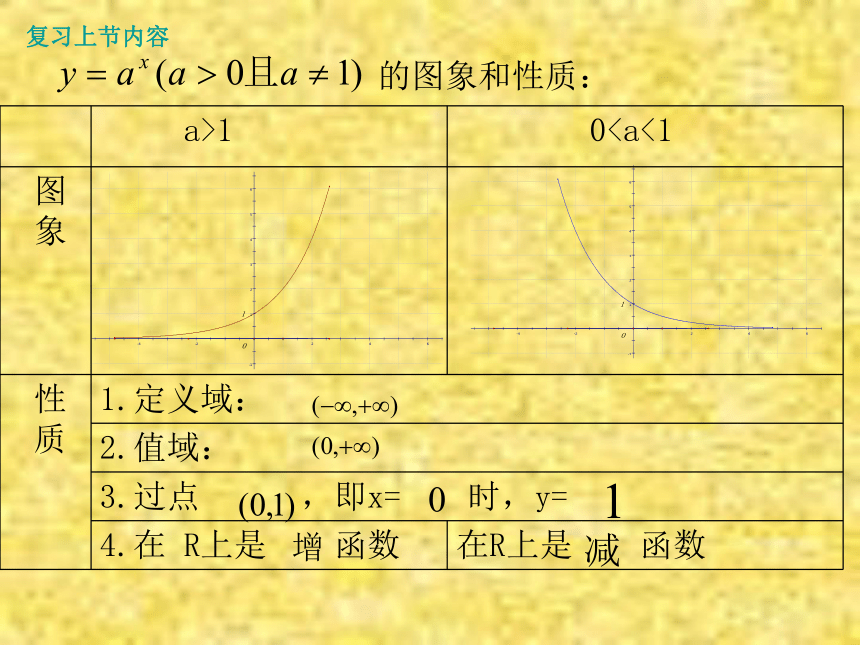
的图象和性质：
a>1 0图
象
性
质 1.定义域：
2.值域：
3.过点 ，即x= 时，y=
4.在 R上是 函数 在R上是 函数
复习上节内容
讲解范例：
例1求下列函数的定义域、值域：
分析：此题要利用指数函数的定义域、值域，并结合
指数函数的图象。注意指数函数的定义域就是使函数
表达式有意义的自变量x的取值范围。
解：（1）由x-1≠0得x≠1所以，所求函数定义域为
{x|x≠1}
⑴
⑵
⑶
由 ，得y≠1
所以，所求函数值域为
{y|y>0且y≠1}
说明：对于值域的求解，可以令
考察指数函数y=
并结合图象
直观地得到:
函数值域为
{y|y>0且y≠1}
⑵
解：（2）
由5x-1≥0得
所以，所求函数定义域为
由
得y≥1
所以，所求函数值域为{y|y≥1}
⑶
解：（3）
所求函数定义域为R
由
可得
所以，所求函数值域为{y|y>1}
x -3 -2 -1 0 1 2 3
0.125 0.25 0.5 1 2 4 8
0.25 0.5 1 2 4 8 16
0.5 1 2 4 8 16 32
例2在同一坐标系下作出下列函数的图象，并指出
它们与指数函数y= 的图象的关系，
与
与
⑴
⑵
解：⑴列出函数数据表,作出图像
比较函数y=
、y=
与y=
的关系：
的图象向左平行移动1个单位长度，
的图象，
的图象向左
平行移动2
个单位长度，
就得到函数
y=
的图象。
将指数函数y=
就得到函数y=
将指数函数y=
x -3 -2 -1 0 1 2 3
0.125 0.25 0.5 1 2 4 8
0.625 0.125 0.25 0.5 1 2 4
0.3125 0.625 0.125 0.25 0.5 1 2
解：⑵列出函数数据表,作出图像
与
⑵
比较函数y=
、y=
与y=
的关系：
的图象向右平行移动1个单位长度，
的图象，
的图象向右
平行移动2
个单位长度，
就得到函数
y=
的图象。
将指数函数y=
就得到函数y=
将指数函数y=
看一看一般情况
小结：小结： 与 的关系：
当m>0时，将指数函数 的图象向右平行移动m个单位长度，就得到函数 的图象；
当m<0时，将指数函数 的图象向左平行移动m个单位长度，就得到函数 的图象。
例2 已知函数
作出函数图像，求定义域、
与
图像的关系。
值域，并探讨
解：
定义域：R 值域：
作出图象如下:
关系：
该部分翻折到
保留
在y轴
右侧的图像,
y轴的左侧,
这个关于y轴
对称的图形就是
的图像
例3 已知函数
作出函数图像，求定义域、
值域。
解：
定义域：R
值域：
函 数 y=f(x)
y=f(x+a)
y=f(x)+a
y=f(-x)
y=-f(x)
y=-f(-x)
y=f(|x|)
y=|f(x)|
对于有些复合函数的图象，则常用基本函数图象+变换方法作出：即把我们熟知的基本函数图象，通过平移、作其对称图等方法，得到我们所要求作的复合函数的图象，这种方法我们遇到的有以下几种形式：
a>0时向左平移a个单位；a<0时向右平移|a|个单位.
a>0时向上平移a个单位；a<0时向下平移|a|个单位.
y=f(-x)与y=f(x)的图象关于y轴对称.
y=-f(x)与y=f(x)的图象关于x轴对称.
y=-f(-x)与y=f(x)的图象关于原点轴对称.
与y=f(x)的图象关于直线y=x对称.
练习：
求下列函数的定义域和值域：
⑴
⑵
解：
⑴要使函数有意义，必须
当
时 ,
；
当
时 ,
∵
∴
∴值域为
⑵要使函数有意义，必须
∵
∴
又∵
∴值域为
课后作业：