第23章旋转 单元测试训练卷 2021-2022学年人教版九年级数学上册(Word版含答案)
文档属性
| 名称 | 第23章旋转 单元测试训练卷 2021-2022学年人教版九年级数学上册(Word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 243.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-28 11:09:17 | ||
图片预览


文档简介
人教版九年级数学上册
第二十三章 旋转
单元测试训练卷
一、选择题(共8小题,4
8=32)
1.
下列图形中不能由一个图形通过旋转而构成的是(
)
A B
C
D
2.
下列图形中是轴对称图形,但不是中心对称图形的是(
)
3.
以原点为中心,将点P(4,5)按逆时针方向旋转90°,得到的点Q关于原点的对称点所在的象限为(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
4.
在平面直角坐标系中,已知点A(-4,3)与点B关于原点对称,则点B的坐标为(
)
A.(-4,-3)
B.(4,3)
C.(4,-3)
D.(-4,3)
5.
如图,在平面直角坐标系中,若△ABC与△A1B1C1关于点E成中心对称,则对称中心E点的坐标是(
)
A.(3,-1)
B.(0,0)
C.(2,-1)
D.(-1,3)
6.
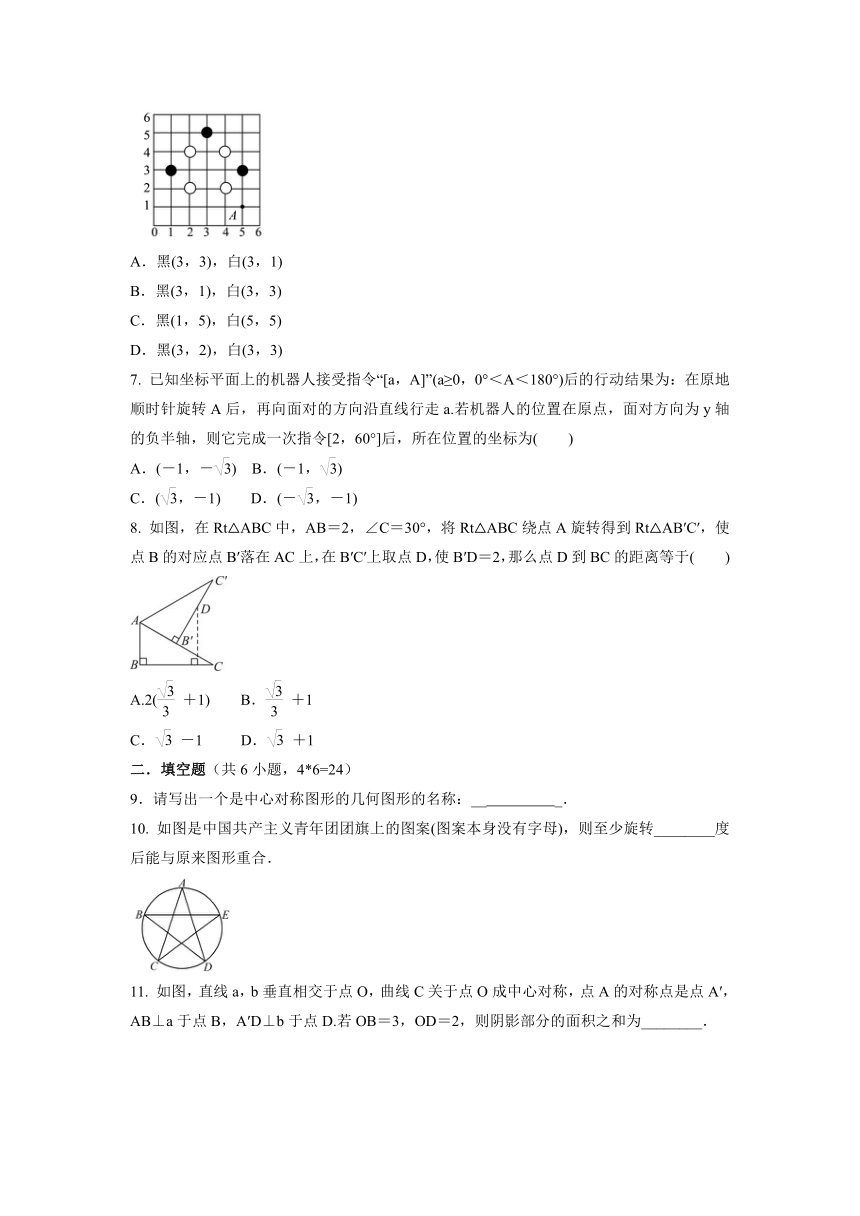
如图,是用围棋子摆出的图案(围棋子的位置用有序数对表示,如点A在(5,1)),如果再摆一黑一白两枚棋子,使9枚棋子组成的图案既是轴对称图形又是中心对称图形,则下列摆放正确的是(
)
A.黑(3,3),白(3,1)
B.黑(3,1),白(3,3)
C.黑(1,5),白(5,5)
D.黑(3,2),白(3,3)
7.
已知坐标平面上的机器人接受指令“[a,A]”(a≥0,0°<A<180°)后的行动结果为:在原地顺时针旋转A后,再向面对的方向沿直线行走a.若机器人的位置在原点,面对方向为y轴的负半轴,则它完成一次指令[2,60°]后,所在位置的坐标为( )
A.(-1,-)
B.(-1,)
C.(,-1)
D.(-,-1)
8.
如图,在Rt△ABC中,AB=2,∠C=30°,将Rt△ABC绕点A旋转得到Rt△AB′C′,使点B的对应点B′落在AC上,在B′C′上取点D,使B′D=2,那么点D到BC的距离等于(
)
A.2(+1)
B.+1
C.-1
D.+1
二.填空题(共6小题,4
6=24)
9.请写出一个是中心对称图形的几何图形的名称:__
_.
10.
如图是中国共产主义青年团团旗上的图案(图案本身没有字母),则至少旋转________度后能与原来图形重合.
11.
如图,直线a,b垂直相交于点O,曲线C关于点O成中心对称,点A的对称点是点A′,AB⊥a于点B,A′D⊥b于点D.若OB=3,OD=2,则阴影部分的面积之和为________.
12.
如图,直线EF过矩形ABCD对角线的交点O,且分别与AB,CD相交于点E,F,若AB=3,BC=4,那么阴影部分的面积为
.
13.
如图,阴影部分组成的图案既是关于x轴成轴对称的图形又是关于坐标原点O成中心对称的图形,若点A的坐标是(1,3),则点M和点N的坐标分别是_________________.
14.
如图,在菱形ABCD中,AB=2,∠BAD=60°,将菱形ABCD绕点A逆时针方向旋转,对应得到菱形AEFG,点E在AC上,EF与CD交于点P,则DP的长是_________________
三.解答题(共5小题,
44分)
15.(6分)
如图,P,Q是方格纸中的两格点,请按要求画出以PQ为对角线的格点四边形.
(1)画出一个面积最小的?PAQB;
(2)画出一个四边形PCQD,使其是轴对称图形而不是中心对称图形,且另一条对角线CD由线段PQ以某一格点为旋转中心旋转得到.
16.(8分)
如图,D是△ABC的边BC的中点,连接AD并延长到点E,使DE=AD,连接BE.
(1)图中哪两个图形成中心对称?
(2)若△ADC的面积为4,求△ABE的面积.
17.(8分)
如图①,已知∠ABC=90°,△ABE是等边三角形,点P为射线BC上任意一点(点P与点B不重合),连接AP,将线段AP绕点A逆时针旋转60°得到线段AQ,连接QE并延长交射线BC于点F.
(1)如图②,当BP=BA时,∠EBF=________°,猜想∠QFC=________°;
(2)如图①,当点P为射线BC上任意一点时,猜想∠QFC的度数,并加以证明.
18.(10分)
如图,在△ABC中,∠BAC=120°,以BC为边向外作等边△BCD,把△ABD绕着点D按顺时针方向旋转60°到△ECD的位置,若AB=3,AC=2,求∠BAD的度数和AD的长.
19.(12分)
将矩形ABCD绕点A顺时针旋转α(0°<α<360°),得到矩形AEFG.
(1)如图,当点E在BD上时.求证:FD=CD;
(2)当α为何值时,GC=GB?画出图形,并说明理由.
参考答案
1-4CBDC
5-8ABDD
9.平行四边形(答案不唯一)
10.72
11.
6
12.3
13.M(-1,-3),N(1,-3)
14.-1
15.解:(1)如图①所示 (2)如图②所示
16.解:(1)△ADC与△EDB成中心对称;
(2)∵△ADC与△EDB关于点D中心对称,∴△ADC≌△EDB,∴S△ADC=S△EDB=4,∵D是BC中点,∴BD=CD,∴S△ABD=S△ACD=4,∴S△ABE=S△ABD+S△BED=8.
17.解:(1)30,60
(2)猜想∠QFC=60°.证明:∠BAP=∠BAE+∠EAP=60°+∠EAP,∠EAQ=∠QAP+∠EAP=60°+∠EAP,∴∠BAP=∠EAQ,在△ABP和△AEQ中,AB=AE,∠BAP=∠EAQ,AQ=AP,∴△ABP≌△AEQ,∴∠AEQ=∠ABP=90°,∴∠BEF=180°-∠AEQ-∠AEB=180°-90°-60°=30°,∴∠QFC=∠EBF+∠BEF=30°+30°=60°
18.
解:由∠BAC=120°知∠ABC+∠ACB=60°.又∵∠ABD=∠ABC+∠CBD=∠DCE,∠CBD=∠BCD=60°,∴∠ACB+∠BCD+∠DCE=∠ACB+∠BCD+∠ABC+∠CBD=180°,即点A,C,E在一条直线上.又∵AD=ED,∠ADE=60°,∴△ADE为等边三角形.∴∠BAD=∠E=60°,AD=AE=AC+CE=AC+AB=2+3=5.
∵∠DPN=∠DCB+∠PNC=∠DCB+∠DBC,∴∠MPN=∠DPM+∠DPN=∠DCE+∠DCB+∠DBC=∠BCE+∠DBC=∠ACB+∠ACE+∠DBC=∠ACB+∠ABD+∠DBC=∠ACB+∠ABC,∵∠BAC=90°,∴∠ACB+∠ABC=90°,∴∠MPN=90°,∴△PMN是等腰直角三角形
19.
解:(1)由旋转可得,AE=AB,∠AEF=∠ABC=∠DAB=90°,EF=BC=AD,∴∠AEB=∠ABE,又∵∠ABE+∠EDA=90°=∠AEB+∠DEF,∴∠EDA=∠DEF,又∵DE=ED,∴△AED≌△FDE(SAS),∴DF=AE,又∵AE=AB=CD,∴FD=CD
(2)当GB=GC时,点G在BC的垂直平分线上,分两种情况讨论:①如图①,当点G在AD右侧时,取BC的中点H,连接GH交AD于点M,∵GC=GB,∴GH⊥BC,∴四边形ABHM是矩形,∴AM=BH=AD=AG,AM∥BH,∴GM垂直平分AD,∴GD=GA=DA,∴△ADG是等边三角形,∴∠DAG=60°,∴旋转角α=60° ②如图②,当点G在AD左侧时,同理可得△ADG是等边三角形,∴∠DAG=60°,∴旋转角α=360°-60°=300°
第二十三章 旋转
单元测试训练卷
一、选择题(共8小题,4
8=32)
1.
下列图形中不能由一个图形通过旋转而构成的是(
)
A B
C
D
2.
下列图形中是轴对称图形,但不是中心对称图形的是(
)
3.
以原点为中心,将点P(4,5)按逆时针方向旋转90°,得到的点Q关于原点的对称点所在的象限为(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
4.
在平面直角坐标系中,已知点A(-4,3)与点B关于原点对称,则点B的坐标为(
)
A.(-4,-3)
B.(4,3)
C.(4,-3)
D.(-4,3)
5.
如图,在平面直角坐标系中,若△ABC与△A1B1C1关于点E成中心对称,则对称中心E点的坐标是(
)
A.(3,-1)
B.(0,0)
C.(2,-1)
D.(-1,3)
6.
如图,是用围棋子摆出的图案(围棋子的位置用有序数对表示,如点A在(5,1)),如果再摆一黑一白两枚棋子,使9枚棋子组成的图案既是轴对称图形又是中心对称图形,则下列摆放正确的是(
)
A.黑(3,3),白(3,1)
B.黑(3,1),白(3,3)
C.黑(1,5),白(5,5)
D.黑(3,2),白(3,3)
7.
已知坐标平面上的机器人接受指令“[a,A]”(a≥0,0°<A<180°)后的行动结果为:在原地顺时针旋转A后,再向面对的方向沿直线行走a.若机器人的位置在原点,面对方向为y轴的负半轴,则它完成一次指令[2,60°]后,所在位置的坐标为( )
A.(-1,-)
B.(-1,)
C.(,-1)
D.(-,-1)
8.
如图,在Rt△ABC中,AB=2,∠C=30°,将Rt△ABC绕点A旋转得到Rt△AB′C′,使点B的对应点B′落在AC上,在B′C′上取点D,使B′D=2,那么点D到BC的距离等于(
)
A.2(+1)
B.+1
C.-1
D.+1
二.填空题(共6小题,4
6=24)
9.请写出一个是中心对称图形的几何图形的名称:__
_.
10.
如图是中国共产主义青年团团旗上的图案(图案本身没有字母),则至少旋转________度后能与原来图形重合.
11.
如图,直线a,b垂直相交于点O,曲线C关于点O成中心对称,点A的对称点是点A′,AB⊥a于点B,A′D⊥b于点D.若OB=3,OD=2,则阴影部分的面积之和为________.
12.
如图,直线EF过矩形ABCD对角线的交点O,且分别与AB,CD相交于点E,F,若AB=3,BC=4,那么阴影部分的面积为
.
13.
如图,阴影部分组成的图案既是关于x轴成轴对称的图形又是关于坐标原点O成中心对称的图形,若点A的坐标是(1,3),则点M和点N的坐标分别是_________________.
14.
如图,在菱形ABCD中,AB=2,∠BAD=60°,将菱形ABCD绕点A逆时针方向旋转,对应得到菱形AEFG,点E在AC上,EF与CD交于点P,则DP的长是_________________
三.解答题(共5小题,
44分)
15.(6分)
如图,P,Q是方格纸中的两格点,请按要求画出以PQ为对角线的格点四边形.
(1)画出一个面积最小的?PAQB;
(2)画出一个四边形PCQD,使其是轴对称图形而不是中心对称图形,且另一条对角线CD由线段PQ以某一格点为旋转中心旋转得到.
16.(8分)
如图,D是△ABC的边BC的中点,连接AD并延长到点E,使DE=AD,连接BE.
(1)图中哪两个图形成中心对称?
(2)若△ADC的面积为4,求△ABE的面积.
17.(8分)
如图①,已知∠ABC=90°,△ABE是等边三角形,点P为射线BC上任意一点(点P与点B不重合),连接AP,将线段AP绕点A逆时针旋转60°得到线段AQ,连接QE并延长交射线BC于点F.
(1)如图②,当BP=BA时,∠EBF=________°,猜想∠QFC=________°;
(2)如图①,当点P为射线BC上任意一点时,猜想∠QFC的度数,并加以证明.
18.(10分)
如图,在△ABC中,∠BAC=120°,以BC为边向外作等边△BCD,把△ABD绕着点D按顺时针方向旋转60°到△ECD的位置,若AB=3,AC=2,求∠BAD的度数和AD的长.
19.(12分)
将矩形ABCD绕点A顺时针旋转α(0°<α<360°),得到矩形AEFG.
(1)如图,当点E在BD上时.求证:FD=CD;
(2)当α为何值时,GC=GB?画出图形,并说明理由.
参考答案
1-4CBDC
5-8ABDD
9.平行四边形(答案不唯一)
10.72
11.
6
12.3
13.M(-1,-3),N(1,-3)
14.-1
15.解:(1)如图①所示 (2)如图②所示
16.解:(1)△ADC与△EDB成中心对称;
(2)∵△ADC与△EDB关于点D中心对称,∴△ADC≌△EDB,∴S△ADC=S△EDB=4,∵D是BC中点,∴BD=CD,∴S△ABD=S△ACD=4,∴S△ABE=S△ABD+S△BED=8.
17.解:(1)30,60
(2)猜想∠QFC=60°.证明:∠BAP=∠BAE+∠EAP=60°+∠EAP,∠EAQ=∠QAP+∠EAP=60°+∠EAP,∴∠BAP=∠EAQ,在△ABP和△AEQ中,AB=AE,∠BAP=∠EAQ,AQ=AP,∴△ABP≌△AEQ,∴∠AEQ=∠ABP=90°,∴∠BEF=180°-∠AEQ-∠AEB=180°-90°-60°=30°,∴∠QFC=∠EBF+∠BEF=30°+30°=60°
18.
解:由∠BAC=120°知∠ABC+∠ACB=60°.又∵∠ABD=∠ABC+∠CBD=∠DCE,∠CBD=∠BCD=60°,∴∠ACB+∠BCD+∠DCE=∠ACB+∠BCD+∠ABC+∠CBD=180°,即点A,C,E在一条直线上.又∵AD=ED,∠ADE=60°,∴△ADE为等边三角形.∴∠BAD=∠E=60°,AD=AE=AC+CE=AC+AB=2+3=5.
∵∠DPN=∠DCB+∠PNC=∠DCB+∠DBC,∴∠MPN=∠DPM+∠DPN=∠DCE+∠DCB+∠DBC=∠BCE+∠DBC=∠ACB+∠ACE+∠DBC=∠ACB+∠ABD+∠DBC=∠ACB+∠ABC,∵∠BAC=90°,∴∠ACB+∠ABC=90°,∴∠MPN=90°,∴△PMN是等腰直角三角形
19.
解:(1)由旋转可得,AE=AB,∠AEF=∠ABC=∠DAB=90°,EF=BC=AD,∴∠AEB=∠ABE,又∵∠ABE+∠EDA=90°=∠AEB+∠DEF,∴∠EDA=∠DEF,又∵DE=ED,∴△AED≌△FDE(SAS),∴DF=AE,又∵AE=AB=CD,∴FD=CD
(2)当GB=GC时,点G在BC的垂直平分线上,分两种情况讨论:①如图①,当点G在AD右侧时,取BC的中点H,连接GH交AD于点M,∵GC=GB,∴GH⊥BC,∴四边形ABHM是矩形,∴AM=BH=AD=AG,AM∥BH,∴GM垂直平分AD,∴GD=GA=DA,∴△ADG是等边三角形,∴∠DAG=60°,∴旋转角α=60° ②如图②,当点G在AD左侧时,同理可得△ADG是等边三角形,∴∠DAG=60°,∴旋转角α=360°-60°=300°
同课章节目录
