沪教版(上海)数学高三上册-15.6球面距离_(课件)
文档属性
| 名称 | 沪教版(上海)数学高三上册-15.6球面距离_(课件) |

|
|
| 格式 | ppt | ||
| 文件大小 | 508.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-29 00:00:00 | ||
图片预览




文档简介
(共10张PPT)
球面上两点间的距离
平面上两点间的最短距离是连结这两点的线段的长度
而球的表面是曲面,球面上P、Q
两点间的最短距离显然不是线段PQ的长度,那是什么呢?
球面上两点之间的最短连线的长度,就是经过这两点的大圆在这两点间的一段劣弧的长度.我们把这个弧长叫做两点的球面距离
问题1:
直观的观察,
在过A,B点的球的截面中半径最大的是
过A,B的圆中,半径越大,
在A,B之间的劣弧的长越小!
过球心的大圆
发现:
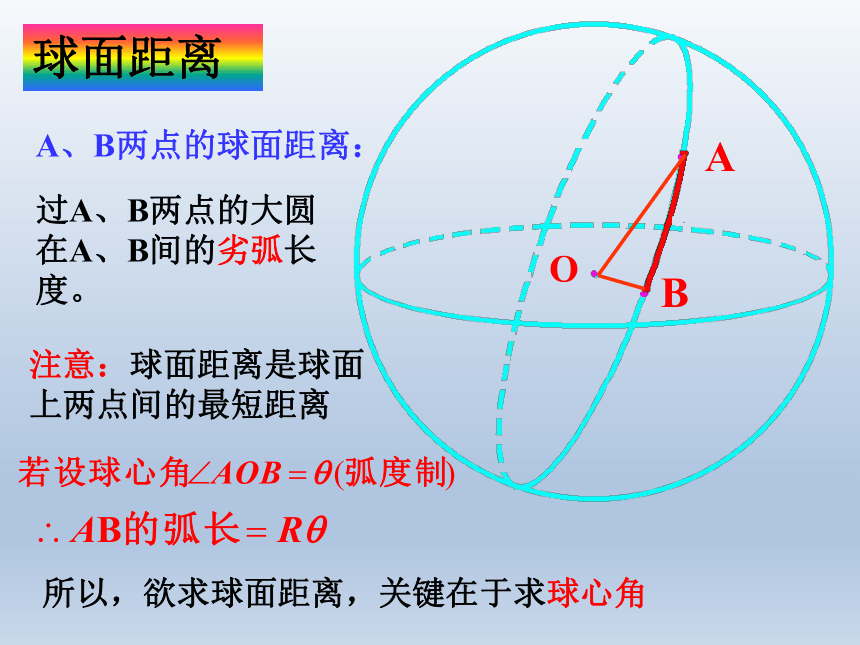
球面距离
A
B
O
A、B两点的球面距离:
过A、B两点的大圆在A、B间的劣弧长度。
注意:球面距离是球面上两点间的最短距离
所以,欲求球面距离,关键在于求球心角
地球仪中的经纬度
经度——P点的经度,也是
或
的度数,即:某地点的经度就是经过这点的经线和地轴确定的半平面与本初子午线与地轴确定的半平面所成二面角的平面角的度数.
A
B
O1
O
α
如图,∠AOB的大小即为B点所在的纬度。
纬度——B点的纬度,即经过这点的球半径和赤道平面所成的角度(即线面角).
例1、
已知地球的半径为
6371km,上海的位置约为东经1210,北纬310,台北的位置约为东经1210,北纬250,
求两个城市间的距离。
例2、
已知地球的半径为
6371km,北京的位置约为东经1160,北纬400,纽约的位置约为西经740,北纬400,
求两个城市间的距离。
练习、把地球当作半径为R的球,地球上A,B两点都在北纬450的纬线上,A,B两点的球面距离是
,A在东经200,求B点的位置
O
例3、球面上有三个点,其中任意两点的球面距离都等于大圆周长的
,经过三个点的小圆的周长为
,求这个球的半径。
球面上两点间的距离
平面上两点间的最短距离是连结这两点的线段的长度
而球的表面是曲面,球面上P、Q
两点间的最短距离显然不是线段PQ的长度,那是什么呢?
球面上两点之间的最短连线的长度,就是经过这两点的大圆在这两点间的一段劣弧的长度.我们把这个弧长叫做两点的球面距离
问题1:
直观的观察,
在过A,B点的球的截面中半径最大的是
过A,B的圆中,半径越大,
在A,B之间的劣弧的长越小!
过球心的大圆
发现:
球面距离
A
B
O
A、B两点的球面距离:
过A、B两点的大圆在A、B间的劣弧长度。
注意:球面距离是球面上两点间的最短距离
所以,欲求球面距离,关键在于求球心角
地球仪中的经纬度
经度——P点的经度,也是
或
的度数,即:某地点的经度就是经过这点的经线和地轴确定的半平面与本初子午线与地轴确定的半平面所成二面角的平面角的度数.
A
B
O1
O
α
如图,∠AOB的大小即为B点所在的纬度。
纬度——B点的纬度,即经过这点的球半径和赤道平面所成的角度(即线面角).
例1、
已知地球的半径为
6371km,上海的位置约为东经1210,北纬310,台北的位置约为东经1210,北纬250,
求两个城市间的距离。
例2、
已知地球的半径为
6371km,北京的位置约为东经1160,北纬400,纽约的位置约为西经740,北纬400,
求两个城市间的距离。
练习、把地球当作半径为R的球,地球上A,B两点都在北纬450的纬线上,A,B两点的球面距离是
,A在东经200,求B点的位置
O
例3、球面上有三个点,其中任意两点的球面距离都等于大圆周长的
,经过三个点的小圆的周长为
,求这个球的半径。
