沪教版(上海)数学高三上册-16.2 排列_8(课件)(共37张PPT)
文档属性
| 名称 | 沪教版(上海)数学高三上册-16.2 排列_8(课件)(共37张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-29 12:35:42 | ||
图片预览











文档简介
(共37张PPT)
排列的概念及简单排列问题
排 列
1.理解并掌握排列的概念.
2.能正确写出一些简单排列问题的所有排列.
1.排列概念的理解.(难点)
2.排列的简单应用.(重点)
3.排列与排列个数的区别.(易混点)
2009年10月底,温家宝总理来到山东费县第一中学视察,听完一节课后与老师们座谈.有12位教师参加,面对总理坐成一排.
问:这12位教师的坐法共有多少种?
排列的相关概念及理解
定义
从n个不同元素中取出m(m≤n)个元素,
,叫做从n个不同元素中取出m个元素的一个排列.
相同
排列
若两个排列相同,则两个排列的元素
,且元素的
也相同.
定义的理解
①定义的两个重要元素:一是“取出元素”,二是“将元素按一定顺序排列”.
②排列不仅与选取的元素有关且与元素的排列顺序有关.
③在定义中规定m≤n,如果m<n,一般称为选排列,如果m=n,则称为全排列.
并按一定顺序排成一列
相同
排列顺序
1.下列问题属于排列问题的是( )
①从10个人中选2人分别去种树和扫地;
②从10个人中选2人去扫地;
③从班上30名男生中选出5人组成一个篮球队;
④从数字5,6,7,8中任取两个不同的数作幂运算.
A.①④
B.①②
C.④
D.①③④
解析: 由排列的定义知,①④为排列问题.
答案: A
2.从4,5,6三个数字中任取两个数字,组成两位数,组成不同的两位数共有( )
A.4个
B.5个
C.6个
D.8个
解析: 从3个数字中选取2个数字组成两位数,共有A32=3×2=6个两位数.
答案: C
3.有5名男生和2名女生,从中选出5人分别担任语文、数字、英语、物理、化学学科的课代表,则不同的选法共有________种.(用数字作答)
解析: 由题意知,从7人中选出5人担任5个学科课代表,共有A75=2
520种不同的选法.
答案: 2
520
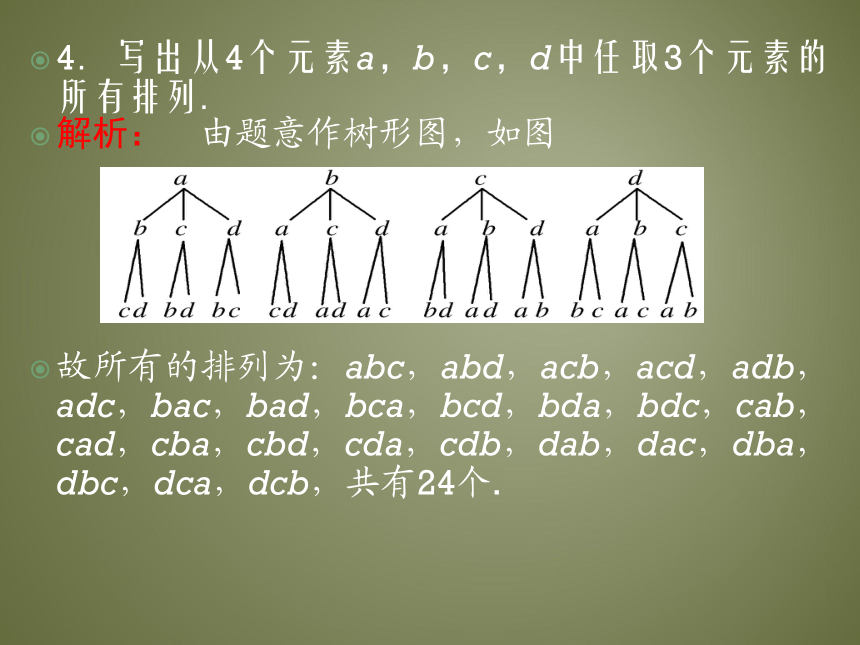
4.写出从4个元素a,b,c,d中任取3个元素的所有排列.
解析: 由题意作树形图,如图
故所有的排列为:abc,abd,acb,acd,adb,adc,bac,bad,bca,bcd,bda,bdc,cab,cad,cba,cbd,cda,cdb,dab,dac,dba,dbc,dca,dcb,共有24个.
下列问题是排列问题吗?请说明理由.
(1)从1、2、3、4四个数字中,任选两个做减法,其结果有多少种不同的可能?
(2)从1、2、3、4四个数字中,任选两个做乘法,其结果有多少种不同的可能?
(3)有12个车站,共需准备多少种车票?
(4)从学号1到10的十名同学中任抽两名同学去学校开座谈会,有多少种选法?
(5)平面上有5个点,其中任意三点不共线,这5点最多可确定多少条直线?
[解题过程]
问题
各问题研析
结果
(1)
由减法及除法定义知,结果都与两数相减的顺序有关,故(1)是排列
(1)(3)
(2)
由加法及乘法定义知,结果都与两数相乘的顺序无关,故(2)不是排列
(3)
车票与始点站和终点站有关,由排列定义知(3)是排列
(4)
所选取两名同学参加座谈会,无顺序之分,故(4)不是排列
(5)
两点确定一条直线,与两点顺序无关,故(5)不是排列
[题后感悟]
判断一个问题是否为排列问题的依据是是否有顺序,有顺序且是从n个不同的元素中任取m(m≤n)个不同的元素的问题就是排列,否则就不是排列,而检验它是否有顺序的依据就是变换元素的位置,看其结果是否有变化,有变化就是有顺序,无变化就是无顺序.
1.判断下列问题是否是排列问题:
(1)从1,2,3,4四个数字中,任选两个做加法,有多少种不同的结果?
(2)从1,2,3,4四个数字中,任选两个做除法,有多少种不同的结果?
(3)某班共有50名同学,现要投票选举正、副班长各一人,共有多少种可能的选举结果?
(4)从2,3,5,7,9中任取两数分别作对数的底数和真数,有多少不同对数值?
(5)从1到10十个自然数中任取两个数组成点的坐标,可得多少个不同的点的坐标?
解析:
(1)由于加法运算满足交换律,所以选出的两个元素做加法时,与两元素的位置无关.故加法不是排列问题.
(2)做除法时,两元素谁做除数,谁做被除数不一样,此时与位置有关,故做除法是排列问题,
(3)是排列问题.选出的2人,担任正、副班长任意,与顺序有关,所以该问题是排列问题.
(4)是排列问题.显然对数值与底数和真数的取值的不同有关系,与顺序有关.
(5)是排列问题.任取两个数组成点的坐标,横、纵坐标的顺序不同,即为不同的坐标,与顺序有关.
(6)不是排列问题.焦点在x轴上的椭圆,方程中的a、b必有a>b,a、b的大小一定.
将玫瑰花、月季花、莲花各一束分别送给甲、乙、丙三人,每人一束,共有多少种不同的分法?请将它们列出来.
利用树形图来表示.
[解题过程]
按分步乘法计数原理的步骤:
第一步,分给甲,有3种分法;
第二步,分给乙,有2种分法;
第三步,分给丙,有1种分法.
故共有3×2×1=6(种)不同的分法.
列出树形图:如下
甲 乙
丙
玫瑰花 月季花 莲花
玫瑰花
莲花
月季花
月季花
玫瑰花
莲花
月季花
莲花
玫瑰花
莲花
玫瑰花
月季花
莲花
月季花
玫瑰花
[题后感悟]
“树形图”在解决排列问题个数不多的情况时,是一种比较有效的表示方式.在操作中先将元素按一定顺序排出,然后以先安排哪个元素为分类标准,进行分类,在每一类中再按余下的元素在前面元素不变的情况下确定第二位元素,再按此元素分类,依次进行,直到完成一个排列,这样能做到不重不漏,然后再按树形图写出排列.
2.北京、上海、香港、台北四个民航站之间的直达航线,需要准备多少种不同的飞机票?将它们列出来.
解析: 先确定起点,有4种方法,再确定终点,有3种方法.由分步乘法计数原理知,共需要4×3=12(种)不同的机票.列举如下:
A,B,C,D四名同学重新换位(每个同学都不能坐其原来的位子),试列出所有可能的换位方法.
(1)本题是一个有限制条件的排列问题;
(2)假设A,B,C,D四名同学原位子分别为1,2,3,4号,则有如下限制条件:
解答本题可以按位置排法的可能性分类,列树形图解决.
坐位号
1
2
3
4
不坐
A
B
C
D
[规范解答]
假设A,B,C,D四名同学原来的位子分别为1,2,3,4号,列出树形图如下:
位置编号
6分
换位后,原来1,2,3,4号座位上坐的同学的所有可能排法有:BADC,BCDA,BDAC,CADB,CDAB,CDBA,DABC,DCAB,DCBA.
12分
[题后感悟]
有限制条件的排列问题应注意限制条件是“位置”还是“元素”,解决这类问题时应注意特殊位置、特殊元素优先考虑的原则,做到不重不漏.有些非数学化的问题,可以转化为数学问题后再求解,为了形象直观,可借助树形图.
3.四人A、B、C、D坐成一排,其中A不坐在排头,写出所有的坐法.
解析:
由“树形图”可知,所有坐法为BACD,BADC,BCAD,BCDA,BDAC,BDCA,CABD,CADB,CBAD,CBDA,CDAB,CDBA,DACB,DABC,DBAC,DBCA,DCAB,DCBA.
1.对排列定义的理解
(1)定义的两个重要因素
一是“取出元素”,二是“将元素按一定顺序排列”,这是排列的两个重要因素,也是与后面将要学习的组合的不同.
(2)每一个排列不仅与选取的元素有关,而且还与元素的排列顺序有关.选取的元素不同或虽元素相同但元素的排列顺序不同时都是不同的排列,只有当两个排列的元素完全相同且元素的顺序完全一样时才是相同的排列.
(3)在定义中规定m≤n,如果m2.如何判断一个具体问题是否为排列问题
(1)首先要保证元素的无重复性,即是从n个不同元素中取出m(m≤n)个不同的元素,否则不是排列问题.
(2)其次要保证元素的有序性,即安排这m个元素时是有顺序的,有序的就是排列,无序的不是排列.而检验它是否有顺序的依据是变换元素的位置,看结果是否发生变化,有变化就是有顺序,无变化就是无顺序.
[特别提醒] 排列的本质特征是每一个排列不仅与所选取的元素有关,而且与这些元素的排列顺序也有关.
◎从1,2,3,4,7,9这六个数中任取两个数分别作为一个对数的底数与真数,可组成多少个不同的对数值?
【错解】 符合条件的对数值可分为两类:
第1类,若1为真数,而2,3,4,7,9中任何一个为底数,得的对数值均为零,仅1个;
第2类,若2,3,4,7,9中任何一个为真数,而不能作底数,其底在余下的4个数中选1个,共有不同的对数值5×4=20(个).
综上,共有21个不同的对数值.
【错因】 审题不细,重复计算.忽略了对数值相同的情况:log24=log39,log42=log93,log23=log49,log32=log94.审题细致,避免重复、遗漏;对数性质loganbn=logab(a>0,a≠1,b>0,n∈N
)
【正解】 分两类:第1类,1作为真数时值为0,仅1个;
第2类,对数的底与真数是从2,3,4,7,9中任取2个的排列有A52=5×4=20(个),共20+1=21(个).
但底数和真数都不相同而对数值相同的有log24=log39,log42=log93,log23=log49,log32=log94,故共有21-4=17个不同的对数值.
排列的概念及简单排列问题
排 列
1.理解并掌握排列的概念.
2.能正确写出一些简单排列问题的所有排列.
1.排列概念的理解.(难点)
2.排列的简单应用.(重点)
3.排列与排列个数的区别.(易混点)
2009年10月底,温家宝总理来到山东费县第一中学视察,听完一节课后与老师们座谈.有12位教师参加,面对总理坐成一排.
问:这12位教师的坐法共有多少种?
排列的相关概念及理解
定义
从n个不同元素中取出m(m≤n)个元素,
,叫做从n个不同元素中取出m个元素的一个排列.
相同
排列
若两个排列相同,则两个排列的元素
,且元素的
也相同.
定义的理解
①定义的两个重要元素:一是“取出元素”,二是“将元素按一定顺序排列”.
②排列不仅与选取的元素有关且与元素的排列顺序有关.
③在定义中规定m≤n,如果m<n,一般称为选排列,如果m=n,则称为全排列.
并按一定顺序排成一列
相同
排列顺序
1.下列问题属于排列问题的是( )
①从10个人中选2人分别去种树和扫地;
②从10个人中选2人去扫地;
③从班上30名男生中选出5人组成一个篮球队;
④从数字5,6,7,8中任取两个不同的数作幂运算.
A.①④
B.①②
C.④
D.①③④
解析: 由排列的定义知,①④为排列问题.
答案: A
2.从4,5,6三个数字中任取两个数字,组成两位数,组成不同的两位数共有( )
A.4个
B.5个
C.6个
D.8个
解析: 从3个数字中选取2个数字组成两位数,共有A32=3×2=6个两位数.
答案: C
3.有5名男生和2名女生,从中选出5人分别担任语文、数字、英语、物理、化学学科的课代表,则不同的选法共有________种.(用数字作答)
解析: 由题意知,从7人中选出5人担任5个学科课代表,共有A75=2
520种不同的选法.
答案: 2
520
4.写出从4个元素a,b,c,d中任取3个元素的所有排列.
解析: 由题意作树形图,如图
故所有的排列为:abc,abd,acb,acd,adb,adc,bac,bad,bca,bcd,bda,bdc,cab,cad,cba,cbd,cda,cdb,dab,dac,dba,dbc,dca,dcb,共有24个.
下列问题是排列问题吗?请说明理由.
(1)从1、2、3、4四个数字中,任选两个做减法,其结果有多少种不同的可能?
(2)从1、2、3、4四个数字中,任选两个做乘法,其结果有多少种不同的可能?
(3)有12个车站,共需准备多少种车票?
(4)从学号1到10的十名同学中任抽两名同学去学校开座谈会,有多少种选法?
(5)平面上有5个点,其中任意三点不共线,这5点最多可确定多少条直线?
[解题过程]
问题
各问题研析
结果
(1)
由减法及除法定义知,结果都与两数相减的顺序有关,故(1)是排列
(1)(3)
(2)
由加法及乘法定义知,结果都与两数相乘的顺序无关,故(2)不是排列
(3)
车票与始点站和终点站有关,由排列定义知(3)是排列
(4)
所选取两名同学参加座谈会,无顺序之分,故(4)不是排列
(5)
两点确定一条直线,与两点顺序无关,故(5)不是排列
[题后感悟]
判断一个问题是否为排列问题的依据是是否有顺序,有顺序且是从n个不同的元素中任取m(m≤n)个不同的元素的问题就是排列,否则就不是排列,而检验它是否有顺序的依据就是变换元素的位置,看其结果是否有变化,有变化就是有顺序,无变化就是无顺序.
1.判断下列问题是否是排列问题:
(1)从1,2,3,4四个数字中,任选两个做加法,有多少种不同的结果?
(2)从1,2,3,4四个数字中,任选两个做除法,有多少种不同的结果?
(3)某班共有50名同学,现要投票选举正、副班长各一人,共有多少种可能的选举结果?
(4)从2,3,5,7,9中任取两数分别作对数的底数和真数,有多少不同对数值?
(5)从1到10十个自然数中任取两个数组成点的坐标,可得多少个不同的点的坐标?
解析:
(1)由于加法运算满足交换律,所以选出的两个元素做加法时,与两元素的位置无关.故加法不是排列问题.
(2)做除法时,两元素谁做除数,谁做被除数不一样,此时与位置有关,故做除法是排列问题,
(3)是排列问题.选出的2人,担任正、副班长任意,与顺序有关,所以该问题是排列问题.
(4)是排列问题.显然对数值与底数和真数的取值的不同有关系,与顺序有关.
(5)是排列问题.任取两个数组成点的坐标,横、纵坐标的顺序不同,即为不同的坐标,与顺序有关.
(6)不是排列问题.焦点在x轴上的椭圆,方程中的a、b必有a>b,a、b的大小一定.
将玫瑰花、月季花、莲花各一束分别送给甲、乙、丙三人,每人一束,共有多少种不同的分法?请将它们列出来.
利用树形图来表示.
[解题过程]
按分步乘法计数原理的步骤:
第一步,分给甲,有3种分法;
第二步,分给乙,有2种分法;
第三步,分给丙,有1种分法.
故共有3×2×1=6(种)不同的分法.
列出树形图:如下
甲 乙
丙
玫瑰花 月季花 莲花
玫瑰花
莲花
月季花
月季花
玫瑰花
莲花
月季花
莲花
玫瑰花
莲花
玫瑰花
月季花
莲花
月季花
玫瑰花
[题后感悟]
“树形图”在解决排列问题个数不多的情况时,是一种比较有效的表示方式.在操作中先将元素按一定顺序排出,然后以先安排哪个元素为分类标准,进行分类,在每一类中再按余下的元素在前面元素不变的情况下确定第二位元素,再按此元素分类,依次进行,直到完成一个排列,这样能做到不重不漏,然后再按树形图写出排列.
2.北京、上海、香港、台北四个民航站之间的直达航线,需要准备多少种不同的飞机票?将它们列出来.
解析: 先确定起点,有4种方法,再确定终点,有3种方法.由分步乘法计数原理知,共需要4×3=12(种)不同的机票.列举如下:
A,B,C,D四名同学重新换位(每个同学都不能坐其原来的位子),试列出所有可能的换位方法.
(1)本题是一个有限制条件的排列问题;
(2)假设A,B,C,D四名同学原位子分别为1,2,3,4号,则有如下限制条件:
解答本题可以按位置排法的可能性分类,列树形图解决.
坐位号
1
2
3
4
不坐
A
B
C
D
[规范解答]
假设A,B,C,D四名同学原来的位子分别为1,2,3,4号,列出树形图如下:
位置编号
6分
换位后,原来1,2,3,4号座位上坐的同学的所有可能排法有:BADC,BCDA,BDAC,CADB,CDAB,CDBA,DABC,DCAB,DCBA.
12分
[题后感悟]
有限制条件的排列问题应注意限制条件是“位置”还是“元素”,解决这类问题时应注意特殊位置、特殊元素优先考虑的原则,做到不重不漏.有些非数学化的问题,可以转化为数学问题后再求解,为了形象直观,可借助树形图.
3.四人A、B、C、D坐成一排,其中A不坐在排头,写出所有的坐法.
解析:
由“树形图”可知,所有坐法为BACD,BADC,BCAD,BCDA,BDAC,BDCA,CABD,CADB,CBAD,CBDA,CDAB,CDBA,DACB,DABC,DBAC,DBCA,DCAB,DCBA.
1.对排列定义的理解
(1)定义的两个重要因素
一是“取出元素”,二是“将元素按一定顺序排列”,这是排列的两个重要因素,也是与后面将要学习的组合的不同.
(2)每一个排列不仅与选取的元素有关,而且还与元素的排列顺序有关.选取的元素不同或虽元素相同但元素的排列顺序不同时都是不同的排列,只有当两个排列的元素完全相同且元素的顺序完全一样时才是相同的排列.
(3)在定义中规定m≤n,如果m
(1)首先要保证元素的无重复性,即是从n个不同元素中取出m(m≤n)个不同的元素,否则不是排列问题.
(2)其次要保证元素的有序性,即安排这m个元素时是有顺序的,有序的就是排列,无序的不是排列.而检验它是否有顺序的依据是变换元素的位置,看结果是否发生变化,有变化就是有顺序,无变化就是无顺序.
[特别提醒] 排列的本质特征是每一个排列不仅与所选取的元素有关,而且与这些元素的排列顺序也有关.
◎从1,2,3,4,7,9这六个数中任取两个数分别作为一个对数的底数与真数,可组成多少个不同的对数值?
【错解】 符合条件的对数值可分为两类:
第1类,若1为真数,而2,3,4,7,9中任何一个为底数,得的对数值均为零,仅1个;
第2类,若2,3,4,7,9中任何一个为真数,而不能作底数,其底在余下的4个数中选1个,共有不同的对数值5×4=20(个).
综上,共有21个不同的对数值.
【错因】 审题不细,重复计算.忽略了对数值相同的情况:log24=log39,log42=log93,log23=log49,log32=log94.审题细致,避免重复、遗漏;对数性质loganbn=logab(a>0,a≠1,b>0,n∈N
)
【正解】 分两类:第1类,1作为真数时值为0,仅1个;
第2类,对数的底与真数是从2,3,4,7,9中任取2个的排列有A52=5×4=20(个),共20+1=21(个).
但底数和真数都不相同而对数值相同的有log24=log39,log42=log93,log23=log49,log32=log94,故共有21-4=17个不同的对数值.
