沪教版(上海)数学高三上册-15.5 几何体的体积_(1)(课件)
文档属性
| 名称 | 沪教版(上海)数学高三上册-15.5 几何体的体积_(1)(课件) |

|
|
| 格式 | ppt | ||
| 文件大小 | 947.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-29 12:40:20 | ||
图片预览



文档简介
(共12张PPT)
回顾
V长方体=abh
=sh
(a-长,b-宽,h-高,
s-底面积)
问题1
长方体的体积?
问题2
体积的概念?
体积——几何体占有空间部分的大小
面积——图形占有平面部分的大小
体积可看成是由面积叠加而成的
立体可看成是由无数个平面叠加而成的
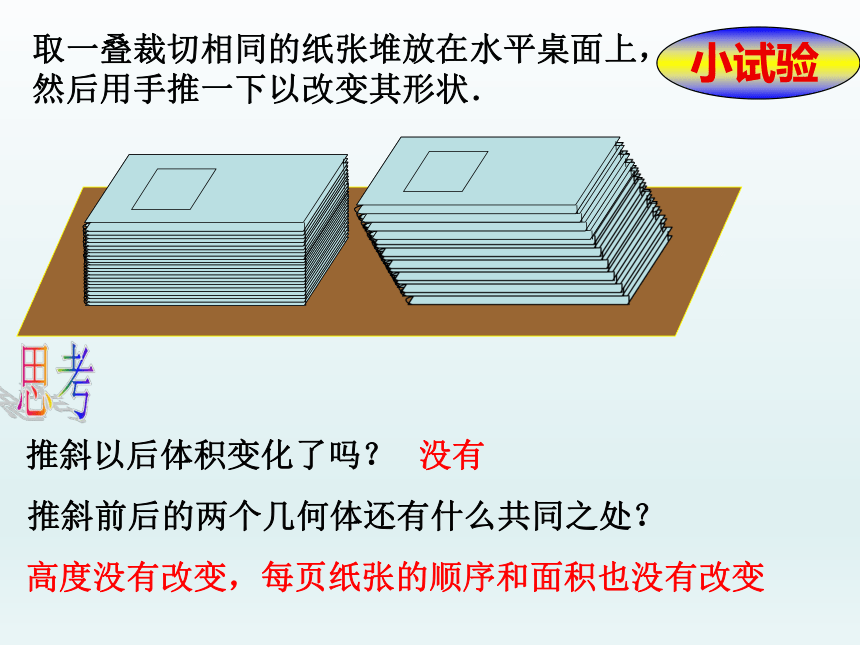
取一叠裁切相同的纸张堆放在水平桌面上,
然后用手推一下以改变其形状.
推斜以后体积变化了吗?
小试验
推斜前后的两个几何体还有什么共同之处?
高度没有改变,每页纸张的顺序和面积也没有改变
没有
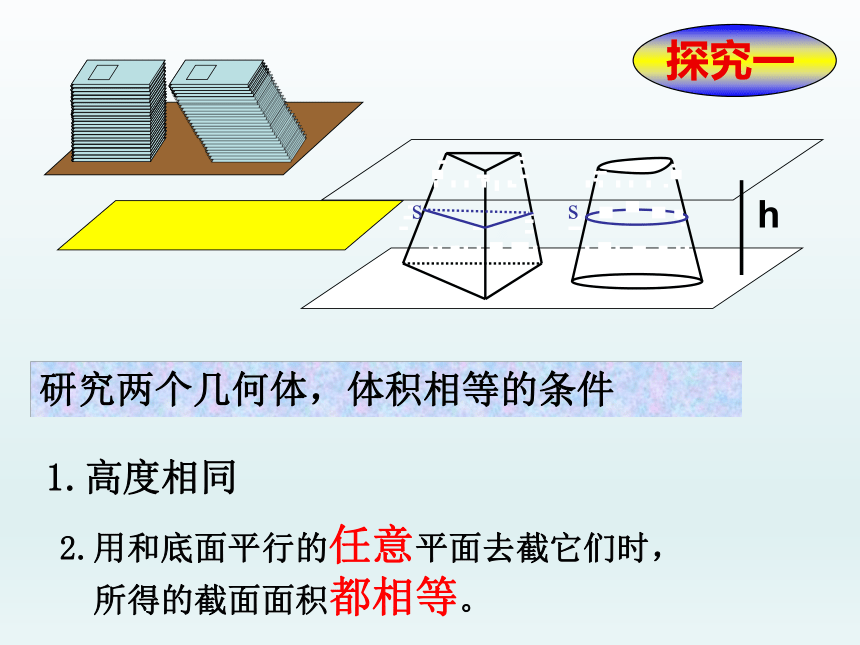
探究一
研究两个几何体,体积相等的条件
1.高度相同
2.用和底面平行的任意平面去截它们时,
所得的截面面积都相等。
s
s
h
祖暅原理
“夫叠棊成立积,缘幂势既同,则积不容异”.
“幂”是指水平截面的面积,“势”是指高.
夹在两个平行平面间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等.
用祖暅原理证明两个几何体体积相等的步骤?
用祖暅原理证明的步骤?
(1)看这两个几何体能否夹在两个平行平面之间;
(2)若能,用平行于这两个平面的任意平面截两个几何体;
(3)看两个截面的面积是否总相等.若是,则满足祖暅原理的条件
三个条件缺一不可,否则不能得出两个几何体的体积一定相等.
α
β
s
s
祖暅原理的功能?
功能二:从一种几何体的体积去得到另一种几何体的体积。
功能一:证明几何体的体积相等.(面积相等推出体积相等)
底面积和高都相等的平行六面体和三棱锥的
体积相等吗?
三棱柱
底面积为S,高为h柱体的体积
等于与它等底等高的长方体的体积
探究二
利用祖暅原理,功能及已有的体积知识
探索底面积为S,高为h柱体体积公式
(1)这三个柱体等高,所以夹在两个平行平面之间;
(2)三个柱体被平行于这两个平面的任意平面所截;
(3)三个截面的面积总相等.
(棱柱的截面性质:平行于
底面的截面与底面全等).
s
s
s
柱体的体积等于它的底面积s和高h的积。
V圆柱=
sh或V圆柱=πr2h
总
结
青藏铁路的某段路基是用碎石铺垫的.已知路基的形
状尺寸如图所示(单位:米),
问每修建1千米铁路需要碎石多少立方米?
1000
直四棱柱的体积计算问题.
实
质
课堂小结
知识方面
本节学习利用祖暅原理获得了柱体的体积公式,并初步体会柱体体积公式的应用;
思维能力方面
体会到联想、类比、猜想、证明等合情推理及逻辑推理的方法在探索新知识方面的重要作用。
回顾
V长方体=abh
=sh
(a-长,b-宽,h-高,
s-底面积)
问题1
长方体的体积?
问题2
体积的概念?
体积——几何体占有空间部分的大小
面积——图形占有平面部分的大小
体积可看成是由面积叠加而成的
立体可看成是由无数个平面叠加而成的
取一叠裁切相同的纸张堆放在水平桌面上,
然后用手推一下以改变其形状.
推斜以后体积变化了吗?
小试验
推斜前后的两个几何体还有什么共同之处?
高度没有改变,每页纸张的顺序和面积也没有改变
没有
探究一
研究两个几何体,体积相等的条件
1.高度相同
2.用和底面平行的任意平面去截它们时,
所得的截面面积都相等。
s
s
h
祖暅原理
“夫叠棊成立积,缘幂势既同,则积不容异”.
“幂”是指水平截面的面积,“势”是指高.
夹在两个平行平面间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等.
用祖暅原理证明两个几何体体积相等的步骤?
用祖暅原理证明的步骤?
(1)看这两个几何体能否夹在两个平行平面之间;
(2)若能,用平行于这两个平面的任意平面截两个几何体;
(3)看两个截面的面积是否总相等.若是,则满足祖暅原理的条件
三个条件缺一不可,否则不能得出两个几何体的体积一定相等.
α
β
s
s
祖暅原理的功能?
功能二:从一种几何体的体积去得到另一种几何体的体积。
功能一:证明几何体的体积相等.(面积相等推出体积相等)
底面积和高都相等的平行六面体和三棱锥的
体积相等吗?
三棱柱
底面积为S,高为h柱体的体积
等于与它等底等高的长方体的体积
探究二
利用祖暅原理,功能及已有的体积知识
探索底面积为S,高为h柱体体积公式
(1)这三个柱体等高,所以夹在两个平行平面之间;
(2)三个柱体被平行于这两个平面的任意平面所截;
(3)三个截面的面积总相等.
(棱柱的截面性质:平行于
底面的截面与底面全等).
s
s
s
柱体的体积等于它的底面积s和高h的积。
V圆柱=
sh或V圆柱=πr2h
总
结
青藏铁路的某段路基是用碎石铺垫的.已知路基的形
状尺寸如图所示(单位:米),
问每修建1千米铁路需要碎石多少立方米?
1000
直四棱柱的体积计算问题.
实
质
课堂小结
知识方面
本节学习利用祖暅原理获得了柱体的体积公式,并初步体会柱体体积公式的应用;
思维能力方面
体会到联想、类比、猜想、证明等合情推理及逻辑推理的方法在探索新知识方面的重要作用。
