沪教版(上海)数学高三上册-16.5 二项式定理_8(课件)(共53张PPT)
文档属性
| 名称 | 沪教版(上海)数学高三上册-16.5 二项式定理_8(课件)(共53张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-29 00:00:00 | ||
图片预览











文档简介
(共53张PPT)
二项式定理
1.
能用计数原理证明二项式定理.
2.
会用二项式定理解决与二项展开式有关的简单问题.
1个重要实质
二项式定理集中体现了二项展开式中的指数、项数、系数的变化的恒等式,其实质是关于a,b,n的恒等式.
3项必须注意
1.
对于二项式定理,不仅要会正用,而且要从整体把握,灵活地应用,如有时可逆用、变形用,对于三项式问题可转化为二项式定理问题去处理.
2.
“赋值法”是求二项展开式系数问题常用的方法,注意取值要有利于问题的解决,可以取一个值或几个值,也可以取几组值,解题易出现漏项等情况,应引起注意.
3.
应用二项式定理时,要把握二项展开式的特点,根据题目要求配、凑、取舍进行放缩处理,从而达到证明或求解之目的.
课前自主导学
1.
二项式定理
(1)二项式定理
公式(a+b)n=________________叫做二项式定理.
(2)二项展开式的通项
Tk+1=________为展开式的第________项.
(3)二项式系数
二项展开式中各项的系数________(k∈{0,1,…,n})叫做二项式系数.
在(a+b)n与(b+a)n的展开式中,其通项相同吗?
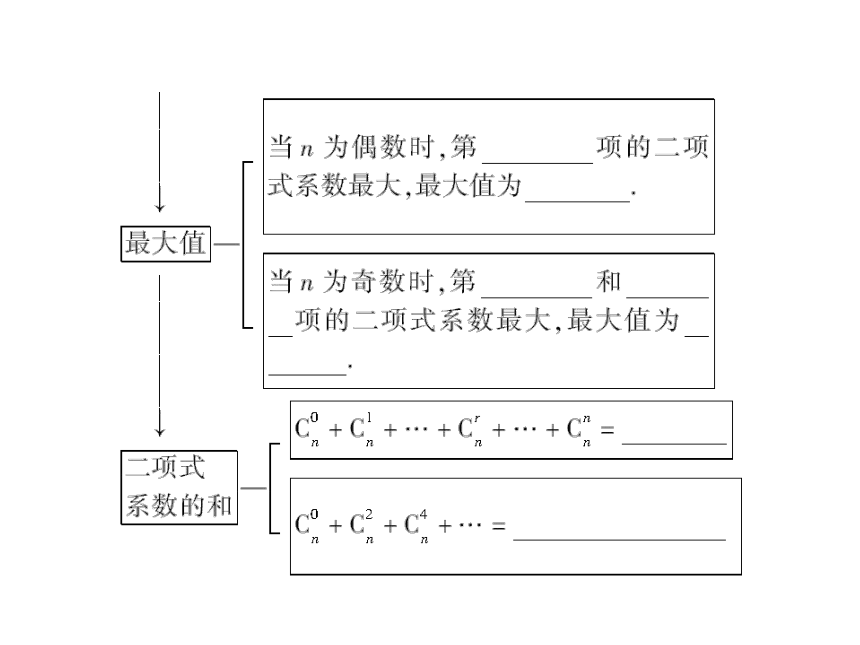
2.二项式系数的性质
二项式系数与项的系数有什么区别?
核心要点研究
[答案] (1)
2 (2)
B
奇思妙想:保持本例(2)中条件不变,则这个展开式中x2的系数.
1.解此类问题可以分两步完成:第一步是根据所给出的条件(特定项)和通项公式,建立方程来确定指数(求解时要注意二项式系数中n和k的隐含条件,即n,k均为非负整数,且n≥k);第二步是根据所求的指数,再求特定项.
2.有理项是字母指数为整数的项.解此类问题必须合并通项公式中同一字母的指数,根据具体要求,令其为整数,再根据数的整除性来求解,若求二项展开式中的整式项,则其通项公式中同一字母的指数应是非负整数,求解方式与求有理项的方式一致.
[答案] (1)56 (2)D
[变式探究] [2013·宜昌段考]在二项式(x-2y)7的展开式中,
(1)求二项式系数之和;
(2)求各项系数之和;
(3)求奇数项系数之和.
例3 [2012·湖北高考]设a∈Z,且0≤a<13,若512012+a能被13整除,则a=( )
A.
0
B.
1
C.
11
D.
12
[审题视点] 对于较大数据的化简,关键是利用二项式定理进行展开.
[答案] D
利用二项式定理解决整除问题时,基本思路是:要证明一个式子能被另一个式子整除,只要证明这个式子按二项式定理展开后的各项均能被另一个式子整除即可.因此,一般将被除式化为含有相关除式的二项式,然后再展开,此时常用“配凑法”、“消去法”结合有关整除知识来处理.
[变式探究] [2013·济宁模拟]22012被9除所得余数是( )
A.
4
B.
5
C.
7
D.
8
答案:A
解析:因为22012=4(23)670=4(9-1)670,根据二项式定理展开可知最后一个因式不能被9整除,那么余数即为4,选A.
[审题视点] (1)可利用“赋值法”求各项系数的和;
(2)可利用展开式中的通项公式确定k的值;
(3)可利用通项公式求出k的范围,再确定项.
分类讨论思想在两个二项式相乘中的应用
[答案] D
【备考·角度说】
No.1 角度关键词:审题视角
两个二项式相乘就是两个多项式相乘,求解时要按照多项式的乘法规则,确定常数项的构成规律,然后进行具体计算.
No.2 角度关键词:方法突破
求几个二项式积的展式中某项的系数或特定项时,一般要根据这几个二项式的结构特征进行分类搭配,分类时要抓住一个二项式逐项分类,分析其它二项式应满足的条件,然后再求解结果,此法易出现分类搭配不全,运算失误等错误.
经典演练提能
答案:C
答案:B
答案:B
答案:B
5.
[2013·金版原创](1-x3)(1+x)10的展开式中,x5的系数是( )
A.
-297
B.
-252
C.
297
D.
207
答案:D
二项式定理
1.
能用计数原理证明二项式定理.
2.
会用二项式定理解决与二项展开式有关的简单问题.
1个重要实质
二项式定理集中体现了二项展开式中的指数、项数、系数的变化的恒等式,其实质是关于a,b,n的恒等式.
3项必须注意
1.
对于二项式定理,不仅要会正用,而且要从整体把握,灵活地应用,如有时可逆用、变形用,对于三项式问题可转化为二项式定理问题去处理.
2.
“赋值法”是求二项展开式系数问题常用的方法,注意取值要有利于问题的解决,可以取一个值或几个值,也可以取几组值,解题易出现漏项等情况,应引起注意.
3.
应用二项式定理时,要把握二项展开式的特点,根据题目要求配、凑、取舍进行放缩处理,从而达到证明或求解之目的.
课前自主导学
1.
二项式定理
(1)二项式定理
公式(a+b)n=________________叫做二项式定理.
(2)二项展开式的通项
Tk+1=________为展开式的第________项.
(3)二项式系数
二项展开式中各项的系数________(k∈{0,1,…,n})叫做二项式系数.
在(a+b)n与(b+a)n的展开式中,其通项相同吗?
2.二项式系数的性质
二项式系数与项的系数有什么区别?
核心要点研究
[答案] (1)
2 (2)
B
奇思妙想:保持本例(2)中条件不变,则这个展开式中x2的系数.
1.解此类问题可以分两步完成:第一步是根据所给出的条件(特定项)和通项公式,建立方程来确定指数(求解时要注意二项式系数中n和k的隐含条件,即n,k均为非负整数,且n≥k);第二步是根据所求的指数,再求特定项.
2.有理项是字母指数为整数的项.解此类问题必须合并通项公式中同一字母的指数,根据具体要求,令其为整数,再根据数的整除性来求解,若求二项展开式中的整式项,则其通项公式中同一字母的指数应是非负整数,求解方式与求有理项的方式一致.
[答案] (1)56 (2)D
[变式探究] [2013·宜昌段考]在二项式(x-2y)7的展开式中,
(1)求二项式系数之和;
(2)求各项系数之和;
(3)求奇数项系数之和.
例3 [2012·湖北高考]设a∈Z,且0≤a<13,若512012+a能被13整除,则a=( )
A.
0
B.
1
C.
11
D.
12
[审题视点] 对于较大数据的化简,关键是利用二项式定理进行展开.
[答案] D
利用二项式定理解决整除问题时,基本思路是:要证明一个式子能被另一个式子整除,只要证明这个式子按二项式定理展开后的各项均能被另一个式子整除即可.因此,一般将被除式化为含有相关除式的二项式,然后再展开,此时常用“配凑法”、“消去法”结合有关整除知识来处理.
[变式探究] [2013·济宁模拟]22012被9除所得余数是( )
A.
4
B.
5
C.
7
D.
8
答案:A
解析:因为22012=4(23)670=4(9-1)670,根据二项式定理展开可知最后一个因式不能被9整除,那么余数即为4,选A.
[审题视点] (1)可利用“赋值法”求各项系数的和;
(2)可利用展开式中的通项公式确定k的值;
(3)可利用通项公式求出k的范围,再确定项.
分类讨论思想在两个二项式相乘中的应用
[答案] D
【备考·角度说】
No.1 角度关键词:审题视角
两个二项式相乘就是两个多项式相乘,求解时要按照多项式的乘法规则,确定常数项的构成规律,然后进行具体计算.
No.2 角度关键词:方法突破
求几个二项式积的展式中某项的系数或特定项时,一般要根据这几个二项式的结构特征进行分类搭配,分类时要抓住一个二项式逐项分类,分析其它二项式应满足的条件,然后再求解结果,此法易出现分类搭配不全,运算失误等错误.
经典演练提能
答案:C
答案:B
答案:B
答案:B
5.
[2013·金版原创](1-x3)(1+x)10的展开式中,x5的系数是( )
A.
-297
B.
-252
C.
297
D.
207
答案:D
