沪教版(上海)数学高三上册-16.5 二项式定理 课件2(共30张PPT)
文档属性
| 名称 | 沪教版(上海)数学高三上册-16.5 二项式定理 课件2(共30张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 641.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-09 00:00:00 | ||
图片预览









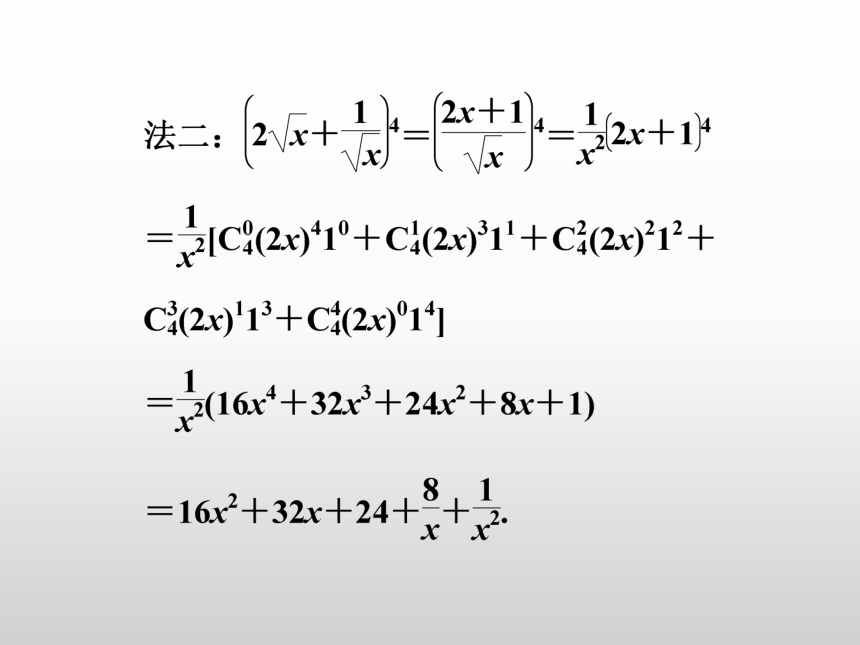

文档简介
(共30张PPT)
二项式定理
学习目标
1.能用计数原理证明二项式定理.
2.掌握二项式定理及其展开式的通项公式.
3.会用二项式定理解决与二项展开式有关的简单问题.
课堂互动讲练
1.3.1
课前自主学案
课前自主学案
1.(a+b)2=__________.
2.(a+b)3=_________________.
温故夯基
a2+2ab+b2
a3+3a2b+3ab2+b3
二项式定理
知新益能
k+1
二项式(a+b)n与(b+a)n的展开式的第k+1项相同吗?
问题探究
课堂互动讲练
正用二项式定理展开二项式
运用二项式定理展开二项式,要记准展开式,对于较复杂的二项式,有时先化简再展开更简捷.
考点突破
例1
【思维总结】 法二较为简单,在展开二项式之前根据二项式的结构特征进行必要变形,可使展开二项式的过程得到简化,例如求(1-x)5(1+x+x2)5的展开式,可将原式变形为(1-x3)5,再展开较为简便.
逆用二项式定理可将多项式化简,对于这类问题的求解,要熟悉公式的特点、项数、各项幂指数的规律以及各项的系数.
逆用二项式定理求“和”
例2
【思路点拨】 共有n+1项,(-2)按升幂排列符合二项式定理形式.
【思维总结】 对于这类问题,从项数、次幂的变化规律,判断是否符合二项式定理.
变式训练 化简:(x-1)5+5(x-1)4+10(x-1)3+10(x-1)2+5(x-1).
求展开式中特定项
例3
【思路点拨】 可先借助通项公式,利用第6项为常数项求n,然后再根据通项公式即可求得(2)、(3).
【思维总结】 对于常数项,隐含条件是字母的指数为0(即0次项);而对于有理项,一般是根据通项公式所得到的项,其所有的字母的指数恰好都是整数的项.解这类问题必须合并通项公式中同一字母的指数,根据具体要求,令其属于整数,再根据数的整除性来求解.若求二项展开式中的整式项,则其通项公式中同一字母的指数应是非负整数,求解方式与求有理项一致.另外,在实际求解时,若通项中含有根式,宜把根式化为分数指数幂,以减少计算中的错误.
利用二项式定理证明或判断整除问题,一般要进行合理变形,常用的变形方法就是拆数,往往是将幂底数写成两数的和,并且其中一个数是除数的倍数,这样能保证被除式展开后的大部分项含有除式的因式,进而可判断或证明被除数能否被除数整除,若不能整除则可求出余数.
整除及余数问题
求230-3除以7的余数.
【思路点拨】 把230改为(23)10=810=(7+1)10.
例4
【误区警示】 此题易误认为余数为-2.
求0.9986的近似值,使误差小于0.001.
用二项式定理求近似值
例5
【思路点拨】 因为0.9986=(1-0.002)6,所以可以用二项式定理来计算.
【解】 0.9986=(1-0.002)6=1+6×(-0.002)+15×(-0.002)2+…+(-0.002)6,
∵T3=15×(-0.002)2=0.00006<0.001.
即第3项以后的项的绝对值都小于0.001,
∴从第3项起,以后的项可以忽略不计,
即0.9986=(1-0.002)6≈1+6×(-0.002)=0.988.
【思维总结】 要根据精确度的要求,取舍后面的项.
方法技巧
1.求展开式的特定项主要方法是利用二项展开式的通项公式来确定通项中k的值或取值范围.处理常数项问题时,抓住此项指数为0是关键.如例2
2.用二项式定理处理整除问题,通常把底数写成除数(或与除数密切关联的数)与某数的和或差的形式,再用二项式定理展开,只考虑后面(或者前面)一、二项就可以了.如例4
方法感悟
失误防范
二项式定理
学习目标
1.能用计数原理证明二项式定理.
2.掌握二项式定理及其展开式的通项公式.
3.会用二项式定理解决与二项展开式有关的简单问题.
课堂互动讲练
1.3.1
课前自主学案
课前自主学案
1.(a+b)2=__________.
2.(a+b)3=_________________.
温故夯基
a2+2ab+b2
a3+3a2b+3ab2+b3
二项式定理
知新益能
k+1
二项式(a+b)n与(b+a)n的展开式的第k+1项相同吗?
问题探究
课堂互动讲练
正用二项式定理展开二项式
运用二项式定理展开二项式,要记准展开式,对于较复杂的二项式,有时先化简再展开更简捷.
考点突破
例1
【思维总结】 法二较为简单,在展开二项式之前根据二项式的结构特征进行必要变形,可使展开二项式的过程得到简化,例如求(1-x)5(1+x+x2)5的展开式,可将原式变形为(1-x3)5,再展开较为简便.
逆用二项式定理可将多项式化简,对于这类问题的求解,要熟悉公式的特点、项数、各项幂指数的规律以及各项的系数.
逆用二项式定理求“和”
例2
【思路点拨】 共有n+1项,(-2)按升幂排列符合二项式定理形式.
【思维总结】 对于这类问题,从项数、次幂的变化规律,判断是否符合二项式定理.
变式训练 化简:(x-1)5+5(x-1)4+10(x-1)3+10(x-1)2+5(x-1).
求展开式中特定项
例3
【思路点拨】 可先借助通项公式,利用第6项为常数项求n,然后再根据通项公式即可求得(2)、(3).
【思维总结】 对于常数项,隐含条件是字母的指数为0(即0次项);而对于有理项,一般是根据通项公式所得到的项,其所有的字母的指数恰好都是整数的项.解这类问题必须合并通项公式中同一字母的指数,根据具体要求,令其属于整数,再根据数的整除性来求解.若求二项展开式中的整式项,则其通项公式中同一字母的指数应是非负整数,求解方式与求有理项一致.另外,在实际求解时,若通项中含有根式,宜把根式化为分数指数幂,以减少计算中的错误.
利用二项式定理证明或判断整除问题,一般要进行合理变形,常用的变形方法就是拆数,往往是将幂底数写成两数的和,并且其中一个数是除数的倍数,这样能保证被除式展开后的大部分项含有除式的因式,进而可判断或证明被除数能否被除数整除,若不能整除则可求出余数.
整除及余数问题
求230-3除以7的余数.
【思路点拨】 把230改为(23)10=810=(7+1)10.
例4
【误区警示】 此题易误认为余数为-2.
求0.9986的近似值,使误差小于0.001.
用二项式定理求近似值
例5
【思路点拨】 因为0.9986=(1-0.002)6,所以可以用二项式定理来计算.
【解】 0.9986=(1-0.002)6=1+6×(-0.002)+15×(-0.002)2+…+(-0.002)6,
∵T3=15×(-0.002)2=0.00006<0.001.
即第3项以后的项的绝对值都小于0.001,
∴从第3项起,以后的项可以忽略不计,
即0.9986=(1-0.002)6≈1+6×(-0.002)=0.988.
【思维总结】 要根据精确度的要求,取舍后面的项.
方法技巧
1.求展开式的特定项主要方法是利用二项展开式的通项公式来确定通项中k的值或取值范围.处理常数项问题时,抓住此项指数为0是关键.如例2
2.用二项式定理处理整除问题,通常把底数写成除数(或与除数密切关联的数)与某数的和或差的形式,再用二项式定理展开,只考虑后面(或者前面)一、二项就可以了.如例4
方法感悟
失误防范
