2022届新高考一轮复习 第三章 函数的概念及基本初等函数 第13讲 函数模型及其运用 教案
文档属性
| 名称 | 2022届新高考一轮复习 第三章 函数的概念及基本初等函数 第13讲 函数模型及其运用 教案 |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-29 12:27:10 | ||
图片预览


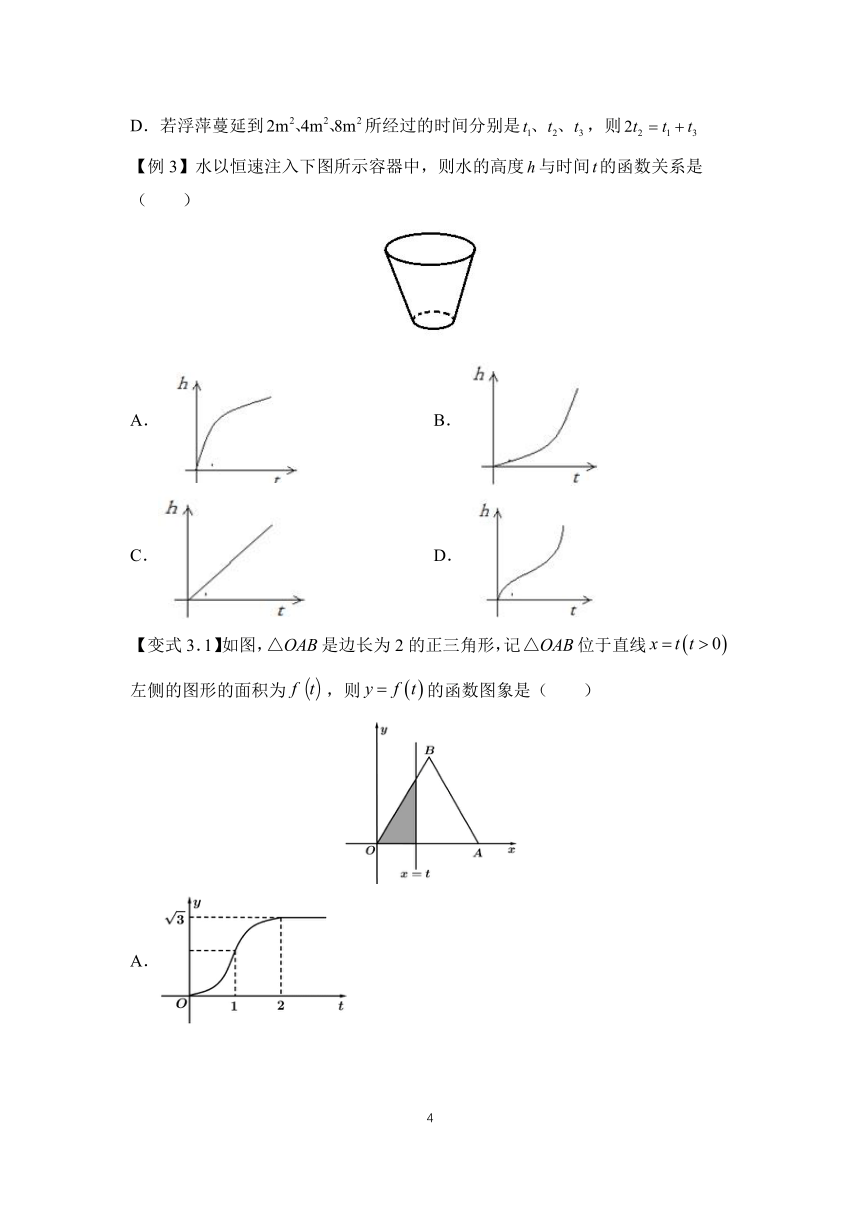
文档简介
第三章
函数的概念及基本初等函数
第13讲
函数模型及其运用
学习要求:
1.了解指数函数、对数函数、幂函数的增长特征,结合具体实例体会直线上升、指数增长、对数增长等不同函数类型增长的含义.
2.了解函数模型(如指数函数、对数函数、幂函数、分段函数等在社会生活中普遍使用的函数模型)的广泛应用.
知识梳理:
1.常见的函数模型
(1)一次函数模型:.
(2)二次函数模型:.
(3)反比例函数模型:.
(4)指数函数模型:.
(5)对数函数模型:.
(6)幂函数模型:.
(7)双勾函数模型:.
2.指数函数、对数函数、幂函数的比较
(1)三种函数的性质
性质
函数
在区间上的单调性
单调递增
单调递增
单调递增
增长速度
越来越快
越来越慢
相对平稳
(2)三种函数之间增长速度的比较
在区间上,函数,,都是增函数,但他们的增长速度不同,随着的增大,的增长速度会越来越快,会超过并远远大于的增长速度;而的增长速度则会越来越慢,图象逐渐表现为与轴趋于平行,因此,总会存在一个,当时,就有.
题型总结:
1利用函数图像刻画实际问题
【例1】下面是一幅统计图,根据此图得到的以下说法中,正确的个数是(
)
①这几年生活水平逐年得到提高;
②生活费收入指数增长最快的一年是2014年;
③生活价格指数上涨速度最快的一年是2015年;
④虽然2016年生活费收入增长缓慢,但生活价格指数也略有降低,因而生活水平有较大的改善.
A.1
B.2
C.3
D.4
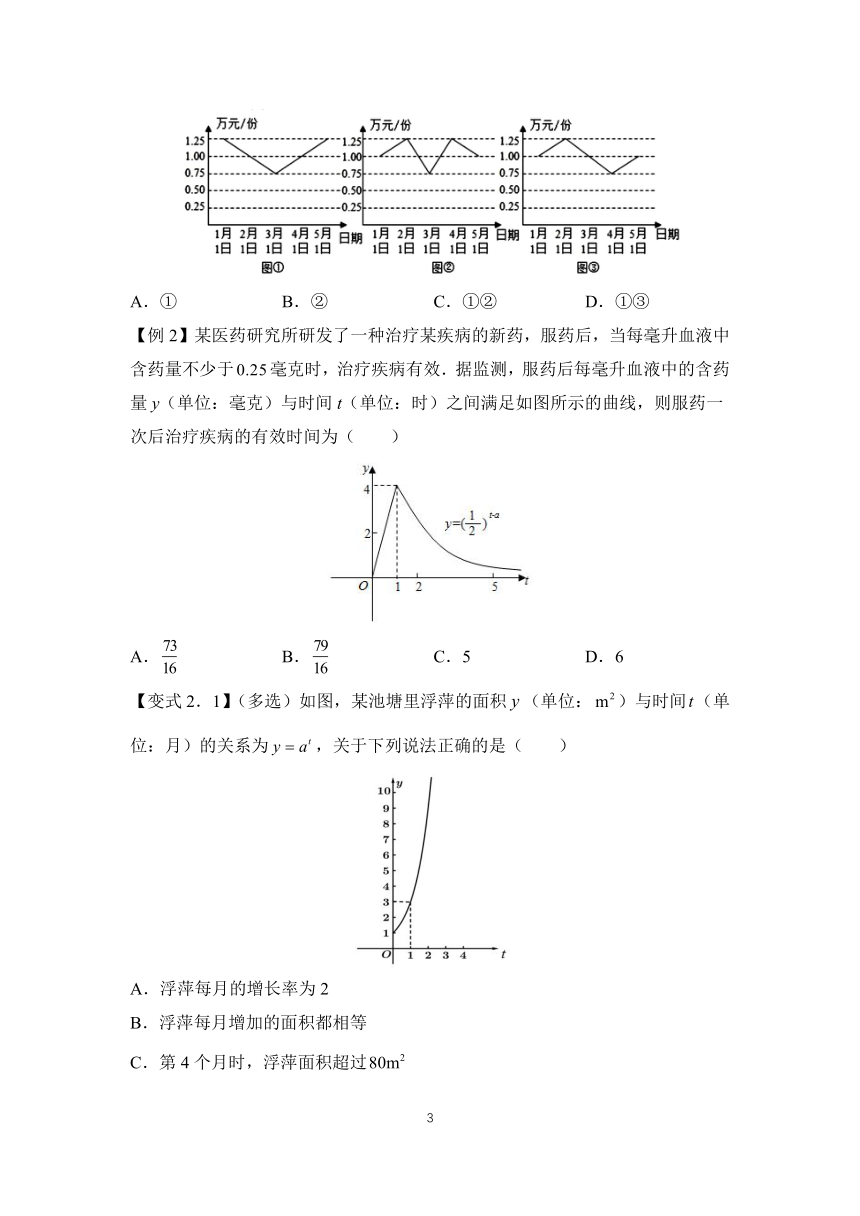
【变式1.1】因市场战略储备的需要,某公司月日起,每月日购买了相同金额的某种物资,连续购买了次.由于市场变化,月日该公司不得不将此物资全部卖出.已知该物资的购买和卖出都是以份为计价单位进行交易,且该公司在买卖的过程中赢利,那么下面三个折线图中反映了这种物资每份价格(单位:万元)的可能变化情况是(
)
A.①
B.②
C.①②
D.①③
【例2】某医药研究所研发了一种治疗某疾病的新药,服药后,当每毫升血液中含药量不少于毫克时,治疗疾病有效.据监测,服药后每毫升血液中的含药量y(单位:毫克)与时间t(单位:时)之间满足如图所示的曲线,则服药一次后治疗疾病的有效时间为(
)
A.
B.
C.5
D.6
【变式2.1】(多选)如图,某池塘里浮萍的面积(单位:)与时间(单位:月)的关系为,关于下列说法正确的是(
)
A.浮萍每月的增长率为2
B.浮萍每月增加的面积都相等
C.第4个月时,浮萍面积超过
D.若浮萍蔓延到所经过的时间分别是,则
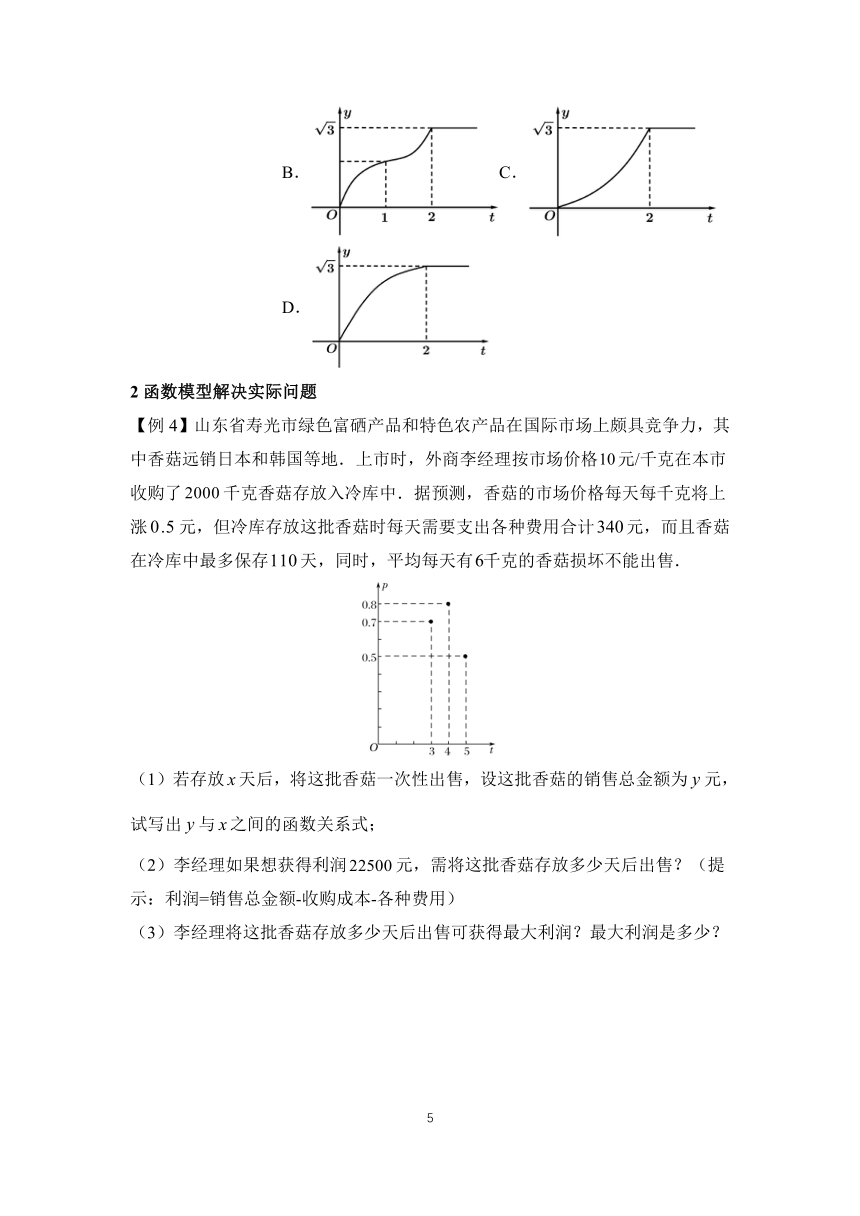
【例3】水以恒速注入下图所示容器中,则水的高度与时间的函数关系是(
)
A.
B.
C.
D.
【变式3.1】如图,是边长为2的正三角形,记位于直线左侧的图形的面积为,则的函数图象是(
)
A.
B.C.
D.
2函数模型解决实际问题
【例4】山东省寿光市绿色富硒产品和特色农产品在国际市场上颇具竞争力,其中香菇远销日本和韩国等地.上市时,外商李经理按市场价格元/千克在本市收购了千克香菇存放入冷库中.据预测,香菇的市场价格每天每千克将上涨元,但冷库存放这批香菇时每天需要支出各种费用合计元,而且香菇在冷库中最多保存天,同时,平均每天有千克的香菇损坏不能出售.
(1)若存放天后,将这批香菇一次性出售,设这批香菇的销售总金额为元,试写出与之间的函数关系式;
(2)李经理如果想获得利润元,需将这批香菇存放多少天后出售?(提示:利润=销售总金额-收购成本-各种费用)
(3)李经理将这批香菇存放多少天后出售可获得最大利润?最大利润是多少?
【变式4.1】在对口扶贫工作中,生态基地种植某中药材的年固定成本为250万元,每产出吨需另外投入可变成本万元,已知.通过市场分析,该中药材可以每吨50万元的价格全部售完.设基地种植该中药材年利润为万元,当基地产出该中药材40吨时,年利润为190万元.
(1)求的值;
(2)求年利润的最大值(精确到万元),并求此时的年产量(精确到吨).
【例5】基本再生数R0与世代间隔T是新冠肺炎的流行病学基本参数.基本再生数指一个感染者传染的平均人数,世代间隔指相邻两代间传染所需的平均时间.在新冠肺炎疫情初始阶段,可以用指数模型:描述累计感染病例数I(t)随时间t(单位:天)的变化规律,指数增长率r与R0,T近似满足.有学者基于已有数据估计出,.据此,在新冠肺炎疫情初始阶段,累计感染病例数增加3倍需要的时间约为(
)
A.天
B.天
C.天
D.天
【变式5.1】“一骑红尘妃子笑,无人知是荔枝来”描述了封建统治者的骄奢生活,同时也讲述了古代资源流通的不便利.如今我国物流行业蓬勃发展,极大地促进了社会经济发展和资源整合.已知某类果蔬的保鲜时间y(单位:小时)与储藏温度x(单位:)满足函数关系(a,b为常数),若该果蔬在的保鲜时间为216小时,在的保鲜时间为8小时,那么在时,该果蔬的保鲜时间为(
)小时.
A.72
B.36
C.24
D.16
【例6】核酸检测分析是用荧光定量法,通过化学物质的荧光信号,对在扩增进程中成指数级增加的靶标实时监测,在扩增的指数时期,荧光信号强度达到阈值时,的数量与扩增次数满足,其中为扩增效率,为的初始数量.已知某被测标本扩增次后,数量变为原来的倍,那么该样本的扩增效率约为(
)
(参考数据:,)
A.
B.
C.
D.
【变式6.1】“喊泉”是一种地下水的毛细现象,人们在泉口吼叫或发出其他声音时,声波传入泉洞内的储水池,进而产生“共鸣”等作用,激起水波,形成涌泉,声音越大,涌起的泉水越高.已知听到的声强与标准声强
(约为,单位:)之比的常用对数称作声强的声强级,记作
(贝尔),即.取贝尔的10倍作为响度的常用单位,简称为分贝,已知某处“喊泉”的声音强度
(分贝)与喷出的泉水高度
()之间满足关系式,甲?乙两名同学大喝一声激起的涌泉的最高高度分别为,.若甲同学大喝一声的声强大约相当于个乙同学同时大喝一声的声强,则的值约为(
)
A.10
B.100
C.200
D.1000
【例7】单位时间内通过道路上指定断面的车辆数被称为“道路容量”,与道路设施、交通服务、环境、气候等诸多条件相关.假设某条道路一小时通过的车辆数满足关系,其中为安全距离,为车速.当安全距离取时,该道路一小时“道路容量”的最大值约为(
)
A.135
B.149
C.165
D.195
【变式7.1】某工厂某种航空产品的年固定成本为万元,每生产件,需另投入成本为,当年产量不足件时,(万元).当年产量不小于件时,(万元).每件商品售价为万元.通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润(万元)关于年产量(件)的函数解析式;
(2)年产量为多少件时,该厂在这一商品的生产中所获利润最大?
.
课后作业:
一、选择题.
1.某食品的保鲜时间(单位:小时)与储藏温度(单位:)满足函数关系,且该食品在的保鲜时间是16小时,已知甲在某日上午10时购买了该食品,并将其遗放在室外,且此日的室外温度随时间变化如图所示,给出以下三个结论,其中,所有正确结论的个数是(
)
①该食品在的保鲜时间是8小时;
②当时,该食品的保鲜时间t随着x增大而减少;
③到了此日15时,甲所购买的食品还在保鲜时间内.
A.2
B.3
C.0
D.1
2.中国茶文化博大精深,茶水的口感与茶叶类型和水的温度有关.经验表明,某种绿茶用的水泡制,再等到茶水温度降至时饮用,可以产生最佳口感.为分析泡制一杯最佳口感茶水所需时间,某硏究人员每隔测量一次茶水的温度,根据所得数据做出如图所示的散点图.观察散点图的分布情况,下列哪个函数模型可以近似地刻画茶水温度随时间变化的规律(
)
A.
B.
C.
D.
3.在新冠肺炎疫情期间,某学校定期对教室进行药熏消毒.教室内每立方米空气中的含药量(单位:毫克)随时间(单位:小时)的变化情况如图所示.在药物释放的过程中,与成正比;药物释放完毕后,与的函数关系式为(为常数).据测定,当空气中每立方米的含药量降低到毫克以下时,学生方可进入教室.那么,从药物释放开始到学生能回到教室,至少在(
)(参考数值).
A.42分钟后
B.48分钟后
C.50分钟后
D.60分钟后
4.“百日冲刺”是各个学校针对高三学生进行的高考前的激情教育,它能在短时间内最大限度激发一个人的潜能,使成绩在原来的基础上有不同程度的提高,以便在高考中取得令人满意的成绩,特别对于成绩在中等偏下的学生来讲,其增加分数的空间尤其大.现有某班主任老师根据历年成绩在中等偏下的学生经历“百日冲刺”之后的成绩变化,构造了一个经过时间(单位:天),增加总分数(单位:分)的函数模型:,为增分转化系数,为“百日冲刺”前的最后一次模考总分,且.现有某学生在高考前天的最后一次模考总分为分,依据此模型估计此学生在高考中可能取得的总分约为(
)()
A.分
B.分
C.分
D.分
5.如图所示,液体从一个圆锥形漏斗漏入一个圆柱形桶中,开始时漏斗中盛满液体,经过3秒漏完,圆柱形桶中液面上升速度是一个常量,则漏斗中液面下降的高度H与下降时间t之间的函数关系的图象只可能是(
)
A.
B.C.
D.
6.“绿水青山就是金山银山”,党的十九大以来,城乡深化河道生态环境治理,科学治污.某乡村一条污染河道的蓄水量为立方米,每天的进出水量为立方米.已知污染源以每天个单位污染河水,某一时段(单位:天)河水污染质量指数为(每立方米河水所含的污染物)满足(为初始质量指数),经测算,河道蓄水量是每天进出水量的80倍.若从现在开始关闭污染源,要使河水的污染水平下降到初始时的10%,需要的时间大约是(参考数据:)(
)
A.1个月
B.3个月
C.半年
D.1年
二、解答题.
7.某民营企业开发出了一种新产品,预计能获得50万元到1500万元的经济收益.企业财务部门研究对开发该新产品的团队进行奖励,并讨论了一个奖励方案:奖金(单位:万元)随经济收益(单位:万元)的增加而增加,且,奖金金额不超过20万元.
(1)请你为该企业构建一个关于的函数模型,并说明你的函数模型符合企业奖励要求的理由;(答案不唯一)
(2)若该企业采用函数作为奖励函数模型,试确定实数的取值范围.
8.某科技公司生产某种芯片.由以往的经验表明,不考虑其他因素,该芯片每日的销售量y(单位:枚)与销售价格x(单位:元/枚,):当时满足关系式,(m,n为常数);当时满足关系式.已知当销售价格为20元/枚时,每日可售出该芯片7000枚;当销售价格为30元/枚时,每日可售出该芯片1500枚.
(1)求m,n的值,并确定y关于x的函数解析式;
(2)若该芯片的成本为10元/枚,试确定销售价格x的值,使公司每日销售该芯片所获利润最大.(x精确到元/枚)
9.经过考察,某公司打算对两个项目进行投资,经测算,投资项目(百万元)与产生的经济效益之间满足:(百万元),投资项目与产生的项目经济效益之间满足:(百万元).
(1)公司现有1200万资金可供投资,应如何分配资金使得投资收益总额最大;
(2)若投资百万元的某项目产生的经济效益为百万元,设投资该项目的边际效应函数为,其边际效应值小于0时,不建议投资该项目,那么对项目与应如何投资,才能使得经济效益最好?
10.某网店有(万件)商品,计划在元旦旺季售出商品x(万件),经市场调查测算,花费t(万元)进行促销后,商品的剩余量与促销费t之间的关系为(其中k为常数),如果不搞促销活动,只能售出1(万件)商品.
(1)要使促销后商品的剩余量不大于(万件),促销费t至少为多少(万元)?
(2)已知商品的进价为32(元/件),另有固定成本3(万元),定义每件售出商品的平均成本为(元),若将商品售价定位:“每件售出商品平均成本的倍”与“每件售出商品平均促销费的一半”之和,则当促销费t为多少(万元)时,该网店售出商品的总利润最大?此时商品的剩余量为多少?
11.上海某工厂以千克/小时的速度匀速生产某种产品,每一小时可获得的利润是元,其中.
(1)要使生产该产品2小时获得的利润不低于30元,求的取值范围;
(2)要使生产900千克该产品获得的利润最大,问:该厂应选取何种生产速度?并求最大利润.
1利用函数图像刻画实际问题
【例1】下面是一幅统计图,根据此图得到的以下说法中,正确的个数是(
)
①这几年生活水平逐年得到提高;
②生活费收入指数增长最快的一年是2014年;
③生活价格指数上涨速度最快的一年是2015年;
④虽然2016年生活费收入增长缓慢,但生活价格指数也略有降低,因而生活水平有较大的改善.
A.1
B.2
C.3
D.4
【答案】C
【解析】由图知,“生活费收入指数”减去“生活价格指数”的差是逐年增大的,故①正确;
“生活费收入指数”在2014~2015年最陡;故②正确;
“生活价格指数”在2015~2016年最平缓,故③不正确;
“生活价格指数”略呈下降,而“生活费收入指数”呈上升趋势,故④正确,
故选C.
【变式1.1】因市场战略储备的需要,某公司月日起,每月日购买了相同金额的某种物资,连续购买了次.由于市场变化,月日该公司不得不将此物资全部卖出.已知该物资的购买和卖出都是以份为计价单位进行交易,且该公司在买卖的过程中赢利,那么下面三个折线图中反映了这种物资每份价格(单位:万元)的可能变化情况是(
)
A.①
B.②
C.①②
D.①③
【答案】D
【解析】设公司每月日用于购买某种物资的金额为万元.
图①中四次购买的物资为(份),
月日一次卖出物资,公司得到,公司盈利,故①满足条件;
图②中四次购买的物资为(份),
月日一次卖出物资,公司得到,公司亏本,故②不满足条件;
图③中四次购买的物资为(份),
月日一次卖出物资,公司得到,公司盈利,故③满足条件,
故选D.
【例2】某医药研究所研发了一种治疗某疾病的新药,服药后,当每毫升血液中含药量不少于毫克时,治疗疾病有效.据监测,服药后每毫升血液中的含药量y(单位:毫克)与时间t(单位:时)之间满足如图所示的曲线,则服药一次后治疗疾病的有效时间为(
)
A.
B.
C.5
D.6
【答案】B
【解析】由题意,当时,函数图象是一个线段,
由于过原点与点,故其解析式为,;
当时,函数的解析式为,
此时在曲线上,将此点的坐标代入函数解析式得,解得,
故函数的解析式为,.
所以.
令,即,解得,
,
服药一次治疗疾病有效的时间为小时,故选B.
【变式2.1】(多选)如图,某池塘里浮萍的面积(单位:)与时间(单位:月)的关系为,关于下列说法正确的是(
)
A.浮萍每月的增长率为2
B.浮萍每月增加的面积都相等
C.第4个月时,浮萍面积超过
D.若浮萍蔓延到所经过的时间分别是,则
【答案】CD
【解析】由图可知,过,所以,,
对A,由为指数函数,为爆炸式增长,
取前三个月浮萍面积,,,故增长率逐月增大,故A错误;
对B,第一个月为,第二个月为,第三个月为,
浮萍每月增加的面积不相等,
对C,,,故C正确;
对D,,,,
所以,,
所以,故D正确,
故选CD.
【例3】水以恒速注入下图所示容器中,则水的高度与时间的函数关系是(
)
A.
B.
C.
D.
【答案】A
【解析】容器由下到上口径越来越大,水以恒速注入,则容器中水的高度增加的速度逐渐变慢,A符合;
B选项容器中水的高度增加的速度逐渐变快;
C选项容器中水的高度是匀速增加;
D选项容器中水的高度增加的速度先增加较慢,后增加较快,
故选A.
【变式3.1】如图,是边长为2的正三角形,记位于直线左侧的图形的面积为,则的函数图象是(
)
A.
B.C.
D.
【答案】A
【解析】根据题意,当时,;
当时,;
当时,,
所以只有A选项符合,故选A.
2函数模型解决实际问题
【例4】山东省寿光市绿色富硒产品和特色农产品在国际市场上颇具竞争力,其中香菇远销日本和韩国等地.上市时,外商李经理按市场价格元/千克在本市收购了千克香菇存放入冷库中.据预测,香菇的市场价格每天每千克将上涨元,但冷库存放这批香菇时每天需要支出各种费用合计元,而且香菇在冷库中最多保存天,同时,平均每天有千克的香菇损坏不能出售.
(1)若存放天后,将这批香菇一次性出售,设这批香菇的销售总金额为元,试写出与之间的函数关系式;
(2)李经理如果想获得利润元,需将这批香菇存放多少天后出售?(提示:利润=销售总金额-收购成本-各种费用)
(3)李经理将这批香菇存放多少天后出售可获得最大利润?最大利润是多少?
【答案】(1);(2)将这批香菇存放天后出售;(3)存放天后出售可获得最大利润为元.
【解析】(1)由题意得,与之间的函数关系式为:
.
(2)由题意得,
化简得,解得,(不合题意,舍去),
因此,李经理如果想获得利润元,需将这批香菇存放天后出售.
(3)设利润为,则由(2)得
,
因此当时,,
又因为,所以李经理将这批香菇存放天后出售可获得最大利润为元.
【变式4.1】在对口扶贫工作中,生态基地种植某中药材的年固定成本为250万元,每产出吨需另外投入可变成本万元,已知.通过市场分析,该中药材可以每吨50万元的价格全部售完.设基地种植该中药材年利润为万元,当基地产出该中药材40吨时,年利润为190万元.
(1)求的值;
(2)求年利润的最大值(精确到万元),并求此时的年产量(精确到吨).
【答案】(1);(2)当年产量约为吨时,年利润最大约为万元.
【解析】(1)由题意,当基地产出该中药材40吨时,年成本为万元,
利润为,解得.
(2)当时,利润为,
因为对称轴,在上为增函数,
所以当时,万元;
当时,,
,
当且仅当,即时取等号,
所以当年产量约为吨时,年利润最大约为万元.
【例5】基本再生数R0与世代间隔T是新冠肺炎的流行病学基本参数.基本再生数指一个感染者传染的平均人数,世代间隔指相邻两代间传染所需的平均时间.在新冠肺炎疫情初始阶段,可以用指数模型:描述累计感染病例数I(t)随时间t(单位:天)的变化规律,指数增长率r与R0,T近似满足.有学者基于已有数据估计出,.据此,在新冠肺炎疫情初始阶段,累计感染病例数增加3倍需要的时间约为(
)
A.天
B.天
C.天
D.天
【答案】D
【解析】把,代入,可得,
,
当时,,则,
两边取对数得,解得,故选D.
【变式5.1】“一骑红尘妃子笑,无人知是荔枝来”描述了封建统治者的骄奢生活,同时也讲述了古代资源流通的不便利.如今我国物流行业蓬勃发展,极大地促进了社会经济发展和资源整合.已知某类果蔬的保鲜时间y(单位:小时)与储藏温度x(单位:)满足函数关系(a,b为常数),若该果蔬在的保鲜时间为216小时,在的保鲜时间为8小时,那么在时,该果蔬的保鲜时间为(
)小时.
A.72
B.36
C.24
D.16
【答案】A
【解析】当时,;当时,,
则,整理可得,于是,
当时,,
故选A.
【例6】核酸检测分析是用荧光定量法,通过化学物质的荧光信号,对在扩增进程中成指数级增加的靶标实时监测,在扩增的指数时期,荧光信号强度达到阈值时,的数量与扩增次数满足,其中为扩增效率,为的初始数量.已知某被测标本扩增次后,数量变为原来的倍,那么该样本的扩增效率约为(
)
(参考数据:,)
A.
B.
C.
D.
【答案】C
【解析】由题意知,,
即,
所以,解得,
故选C.
【变式6.1】“喊泉”是一种地下水的毛细现象,人们在泉口吼叫或发出其他声音时,声波传入泉洞内的储水池,进而产生“共鸣”等作用,激起水波,形成涌泉,声音越大,涌起的泉水越高.已知听到的声强与标准声强
(约为,单位:)之比的常用对数称作声强的声强级,记作
(贝尔),即.取贝尔的10倍作为响度的常用单位,简称为分贝,已知某处“喊泉”的声音强度
(分贝)与喷出的泉水高度
()之间满足关系式,甲?乙两名同学大喝一声激起的涌泉的最高高度分别为,.若甲同学大喝一声的声强大约相当于个乙同学同时大喝一声的声强,则的值约为(
)
A.10
B.100
C.200
D.1000
【答案】B
【解析】设甲同学的声强为,乙同学的声强为,则,,
两式相减即得,即从而,所以的值约为100,
故选B.
【例7】单位时间内通过道路上指定断面的车辆数被称为“道路容量”,与道路设施、交通服务、环境、气候等诸多条件相关.假设某条道路一小时通过的车辆数满足关系,其中为安全距离,为车速.当安全距离取时,该道路一小时“道路容量”的最大值约为(
)
A.135
B.149
C.165
D.195
【答案】B
【解析】由题意得,,
当且仅当,即时取“=”,
所以该道路一小时“道路容量”的最大值约为149,故选B.
【变式7.1】某工厂某种航空产品的年固定成本为万元,每生产件,需另投入成本为,当年产量不足件时,(万元).当年产量不小于件时,(万元).每件商品售价为万元.通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润(万元)关于年产量(件)的函数解析式;
(2)年产量为多少件时,该厂在这一商品的生产中所获利润最大?
【答案】(1);(2)年产量为件时,利润最大为万元.
【解析】(1)当时,;
当时,,
所以.
(2)当时,,
此时,当时,取得最大值万元.
当时,,
此时,当时,即时,取得最大值万元,,
所以年产量为件时,利润最大为万元.
课后作业:
一、选择题.
1.某食品的保鲜时间(单位:小时)与储藏温度(单位:)满足函数关系,且该食品在的保鲜时间是16小时,已知甲在某日上午10时购买了该食品,并将其遗放在室外,且此日的室外温度随时间变化如图所示,给出以下三个结论,其中,所有正确结论的个数是(
)
①该食品在的保鲜时间是8小时;
②当时,该食品的保鲜时间t随着x增大而减少;
③到了此日15时,甲所购买的食品还在保鲜时间内.
A.2
B.3
C.0
D.1
【答案】A
【解析】由题意可得,当时,保鲜时间是16小时,即,解得,
①当时,,故保鲜时间是8小时,故①正确;
②当时,为减函数,则该食品的保鲜时间t随着x增大而减少,故②正确;
③在某日上午10时,温度为8度,此时保鲜时间为小时,到了此日15时,已经过了保鲜时间,所以甲所购买的食品不在保鲜时间内,故③不正确,
故选A.
2.中国茶文化博大精深,茶水的口感与茶叶类型和水的温度有关.经验表明,某种绿茶用的水泡制,再等到茶水温度降至时饮用,可以产生最佳口感.为分析泡制一杯最佳口感茶水所需时间,某硏究人员每隔测量一次茶水的温度,根据所得数据做出如图所示的散点图.观察散点图的分布情况,下列哪个函数模型可以近似地刻画茶水温度随时间变化的规律(
)
A.
B.
C.
D.
【答案】B
【解析】由函数图象可知符合条件的只有指数函数模型,并且,,
故选B.
3.在新冠肺炎疫情期间,某学校定期对教室进行药熏消毒.教室内每立方米空气中的含药量(单位:毫克)随时间(单位:小时)的变化情况如图所示.在药物释放的过程中,与成正比;药物释放完毕后,与的函数关系式为(为常数).据测定,当空气中每立方米的含药量降低到毫克以下时,学生方可进入教室.那么,从药物释放开始到学生能回到教室,至少在(
)(参考数值).
A.42分钟后
B.48分钟后
C.50分钟后
D.60分钟后
【答案】B
【解析】把点代入中,,解得.
所以当时,,
因为当空气中每立方米的含药量降低到毫克以下时,学生方可进入教室,
所以,解得.
至少需要经过分钟后,学生才能回到教室,
故选B.
4.“百日冲刺”是各个学校针对高三学生进行的高考前的激情教育,它能在短时间内最大限度激发一个人的潜能,使成绩在原来的基础上有不同程度的提高,以便在高考中取得令人满意的成绩,特别对于成绩在中等偏下的学生来讲,其增加分数的空间尤其大.现有某班主任老师根据历年成绩在中等偏下的学生经历“百日冲刺”之后的成绩变化,构造了一个经过时间(单位:天),增加总分数(单位:分)的函数模型:,为增分转化系数,为“百日冲刺”前的最后一次模考总分,且.现有某学生在高考前天的最后一次模考总分为分,依据此模型估计此学生在高考中可能取得的总分约为(
)()
A.分
B.分
C.分
D.分
【答案】B
【解析】由题意得:,,
,
该学生在高考中可能取得的总分约为分,故选B.
5.如图所示,液体从一个圆锥形漏斗漏入一个圆柱形桶中,开始时漏斗中盛满液体,经过3秒漏完,圆柱形桶中液面上升速度是一个常量,则漏斗中液面下降的高度H与下降时间t之间的函数关系的图象只可能是(
)
A.
B.C.
D.
【答案】B
【解析】由于所给的圆锥形漏斗上口大于下口,
当时间取时,漏斗中液面下落的高度不会达到漏斗高度的,
对比四个选项的图象可得结果,故选B.
6.“绿水青山就是金山银山”,党的十九大以来,城乡深化河道生态环境治理,科学治污.某乡村一条污染河道的蓄水量为立方米,每天的进出水量为立方米.已知污染源以每天个单位污染河水,某一时段(单位:天)河水污染质量指数为(每立方米河水所含的污染物)满足(为初始质量指数),经测算,河道蓄水量是每天进出水量的80倍.若从现在开始关闭污染源,要使河水的污染水平下降到初始时的10%,需要的时间大约是(参考数据:)(
)
A.1个月
B.3个月
C.半年
D.1年
【答案】C
【解析】由题可知:,∴,
∴,∴(天),
∴要使河水的污染水平下降到初始时的10%,需要的时间大约是半年,
故选C.
二、解答题.
7.某民营企业开发出了一种新产品,预计能获得50万元到1500万元的经济收益.企业财务部门研究对开发该新产品的团队进行奖励,并讨论了一个奖励方案:奖金(单位:万元)随经济收益(单位:万元)的增加而增加,且,奖金金额不超过20万元.
(1)请你为该企业构建一个关于的函数模型,并说明你的函数模型符合企业奖励要求的理由;(答案不唯一)
(2)若该企业采用函数作为奖励函数模型,试确定实数的取值范围.
【答案】(1)答案见解析;(2).
【解析】(1)答案不唯一.构造出一个函数;说明是单调增函数;函数的取值满足要求.
如,,就是符合企业奖励的一个函数模型.
理由:
根据一次函数的性质,易知,随增大而增大,即为增函数;
当时,,
当时,,即奖金金额且不超过20万元.
故该函数是符合企业奖励要求的一个函数模型.
(2)当时,易知是增函数,且当时,,当时,,即满足奖金且不超过20万的要求;
故当时,符合企业奖励要求.
当时,函数是增函数,即对任意,且时,成立.
故当且仅当,即时,此时函数在上是增函数.
由,得;进一步可知,,故成立,即当时,函数符合奖金且金额不超过20万的要求.
依据函数模型是符合企业的奖励要求,即此函数为增函数,
于是,有,解得,
综上,所求实数的取值范围是.
8.某科技公司生产某种芯片.由以往的经验表明,不考虑其他因素,该芯片每日的销售量y(单位:枚)与销售价格x(单位:元/枚,):当时满足关系式,(m,n为常数);当时满足关系式.已知当销售价格为20元/枚时,每日可售出该芯片7000枚;当销售价格为30元/枚时,每日可售出该芯片1500枚.
(1)求m,n的值,并确定y关于x的函数解析式;
(2)若该芯片的成本为10元/枚,试确定销售价格x的值,使公司每日销售该芯片所获利润最大.(x精确到元/枚)
【答案】(1),,;(2).
【解析】(1)因为时,;时,,
所以,解得,,
每日的销售量.
(2)由(1)知,当时:每日销售利润
,.
则,
当或时,,
当时,,单调递增;
当时,,单调递减,
是函数在上的唯一极大值点,;
当时:每日销售利润,
在有最大值,且.
综上,销售价格元/枚时,每日利润最大.
9.经过考察,某公司打算对两个项目进行投资,经测算,投资项目(百万元)与产生的经济效益之间满足:(百万元),投资项目与产生的项目经济效益之间满足:(百万元).
(1)公司现有1200万资金可供投资,应如何分配资金使得投资收益总额最大;
(2)若投资百万元的某项目产生的经济效益为百万元,设投资该项目的边际效应函数为,其边际效应值小于0时,不建议投资该项目,那么对项目与应如何投资,才能使得经济效益最好?
【答案】(1)A、B项目各6百万,收益最大为3400万;(2)A、B项目各550万.
【解析】(1)投资项目(百万元),则投资项目(百万元),
投资收益总额
,时取最大值,
即投资项目6百万,投资项目6百万,收益总额最大为万元.
(2)若投资项目(百万元),则,解得,
投资项目万元;
若投资项目(百万元),则,
解得,
应投资项目万元,
即两个项目各投资550万元时,经济效益最好.
10.某网店有(万件)商品,计划在元旦旺季售出商品x(万件),经市场调查测算,花费t(万元)进行促销后,商品的剩余量与促销费t之间的关系为(其中k为常数),如果不搞促销活动,只能售出1(万件)商品.
(1)要使促销后商品的剩余量不大于(万件),促销费t至少为多少(万元)?
(2)已知商品的进价为32(元/件),另有固定成本3(万元),定义每件售出商品的平均成本为(元),若将商品售价定位:“每件售出商品平均成本的倍”与“每件售出商品平均促销费的一半”之和,则当促销费t为多少(万元)时,该网店售出商品的总利润最大?此时商品的剩余量为多少?
【答案】(1)(万元);(2)当促销费为7万元时,网店利润的最大为42万元,此时商品的剩余量为(万件).
【解析】(1)由,当时,,得,∴,
由,解得,
所以促销费至少为19万元.
(2)网店的利润y(万元),
由题意可得
,
当且仅当,即时取等号,此时,
所以当促销费为7万元时,网店利润的最大为42万元,此时商品的剩余量为
(万件).
11.上海某工厂以千克/小时的速度匀速生产某种产品,每一小时可获得的利润是元,其中.
(1)要使生产该产品2小时获得的利润不低于30元,求的取值范围;
(2)要使生产900千克该产品获得的利润最大,问:该厂应选取何种生产速度?并求最大利润.
【答案】(1);(2),4575元.
【解析】(1),即,
整理可得,解得或
(舍去),
所以.
(2)要使生产900千克该产品获得的利润最大时为y,
,
,所以当,取最大值为4575元.
2
函数的概念及基本初等函数
第13讲
函数模型及其运用
学习要求:
1.了解指数函数、对数函数、幂函数的增长特征,结合具体实例体会直线上升、指数增长、对数增长等不同函数类型增长的含义.
2.了解函数模型(如指数函数、对数函数、幂函数、分段函数等在社会生活中普遍使用的函数模型)的广泛应用.
知识梳理:
1.常见的函数模型
(1)一次函数模型:.
(2)二次函数模型:.
(3)反比例函数模型:.
(4)指数函数模型:.
(5)对数函数模型:.
(6)幂函数模型:.
(7)双勾函数模型:.
2.指数函数、对数函数、幂函数的比较
(1)三种函数的性质
性质
函数
在区间上的单调性
单调递增
单调递增
单调递增
增长速度
越来越快
越来越慢
相对平稳
(2)三种函数之间增长速度的比较
在区间上,函数,,都是增函数,但他们的增长速度不同,随着的增大,的增长速度会越来越快,会超过并远远大于的增长速度;而的增长速度则会越来越慢,图象逐渐表现为与轴趋于平行,因此,总会存在一个,当时,就有.
题型总结:
1利用函数图像刻画实际问题
【例1】下面是一幅统计图,根据此图得到的以下说法中,正确的个数是(
)
①这几年生活水平逐年得到提高;
②生活费收入指数增长最快的一年是2014年;
③生活价格指数上涨速度最快的一年是2015年;
④虽然2016年生活费收入增长缓慢,但生活价格指数也略有降低,因而生活水平有较大的改善.
A.1
B.2
C.3
D.4
【变式1.1】因市场战略储备的需要,某公司月日起,每月日购买了相同金额的某种物资,连续购买了次.由于市场变化,月日该公司不得不将此物资全部卖出.已知该物资的购买和卖出都是以份为计价单位进行交易,且该公司在买卖的过程中赢利,那么下面三个折线图中反映了这种物资每份价格(单位:万元)的可能变化情况是(
)
A.①
B.②
C.①②
D.①③
【例2】某医药研究所研发了一种治疗某疾病的新药,服药后,当每毫升血液中含药量不少于毫克时,治疗疾病有效.据监测,服药后每毫升血液中的含药量y(单位:毫克)与时间t(单位:时)之间满足如图所示的曲线,则服药一次后治疗疾病的有效时间为(
)
A.
B.
C.5
D.6
【变式2.1】(多选)如图,某池塘里浮萍的面积(单位:)与时间(单位:月)的关系为,关于下列说法正确的是(
)
A.浮萍每月的增长率为2
B.浮萍每月增加的面积都相等
C.第4个月时,浮萍面积超过
D.若浮萍蔓延到所经过的时间分别是,则
【例3】水以恒速注入下图所示容器中,则水的高度与时间的函数关系是(
)
A.
B.
C.
D.
【变式3.1】如图,是边长为2的正三角形,记位于直线左侧的图形的面积为,则的函数图象是(
)
A.
B.C.
D.
2函数模型解决实际问题
【例4】山东省寿光市绿色富硒产品和特色农产品在国际市场上颇具竞争力,其中香菇远销日本和韩国等地.上市时,外商李经理按市场价格元/千克在本市收购了千克香菇存放入冷库中.据预测,香菇的市场价格每天每千克将上涨元,但冷库存放这批香菇时每天需要支出各种费用合计元,而且香菇在冷库中最多保存天,同时,平均每天有千克的香菇损坏不能出售.
(1)若存放天后,将这批香菇一次性出售,设这批香菇的销售总金额为元,试写出与之间的函数关系式;
(2)李经理如果想获得利润元,需将这批香菇存放多少天后出售?(提示:利润=销售总金额-收购成本-各种费用)
(3)李经理将这批香菇存放多少天后出售可获得最大利润?最大利润是多少?
【变式4.1】在对口扶贫工作中,生态基地种植某中药材的年固定成本为250万元,每产出吨需另外投入可变成本万元,已知.通过市场分析,该中药材可以每吨50万元的价格全部售完.设基地种植该中药材年利润为万元,当基地产出该中药材40吨时,年利润为190万元.
(1)求的值;
(2)求年利润的最大值(精确到万元),并求此时的年产量(精确到吨).
【例5】基本再生数R0与世代间隔T是新冠肺炎的流行病学基本参数.基本再生数指一个感染者传染的平均人数,世代间隔指相邻两代间传染所需的平均时间.在新冠肺炎疫情初始阶段,可以用指数模型:描述累计感染病例数I(t)随时间t(单位:天)的变化规律,指数增长率r与R0,T近似满足.有学者基于已有数据估计出,.据此,在新冠肺炎疫情初始阶段,累计感染病例数增加3倍需要的时间约为(
)
A.天
B.天
C.天
D.天
【变式5.1】“一骑红尘妃子笑,无人知是荔枝来”描述了封建统治者的骄奢生活,同时也讲述了古代资源流通的不便利.如今我国物流行业蓬勃发展,极大地促进了社会经济发展和资源整合.已知某类果蔬的保鲜时间y(单位:小时)与储藏温度x(单位:)满足函数关系(a,b为常数),若该果蔬在的保鲜时间为216小时,在的保鲜时间为8小时,那么在时,该果蔬的保鲜时间为(
)小时.
A.72
B.36
C.24
D.16
【例6】核酸检测分析是用荧光定量法,通过化学物质的荧光信号,对在扩增进程中成指数级增加的靶标实时监测,在扩增的指数时期,荧光信号强度达到阈值时,的数量与扩增次数满足,其中为扩增效率,为的初始数量.已知某被测标本扩增次后,数量变为原来的倍,那么该样本的扩增效率约为(
)
(参考数据:,)
A.
B.
C.
D.
【变式6.1】“喊泉”是一种地下水的毛细现象,人们在泉口吼叫或发出其他声音时,声波传入泉洞内的储水池,进而产生“共鸣”等作用,激起水波,形成涌泉,声音越大,涌起的泉水越高.已知听到的声强与标准声强
(约为,单位:)之比的常用对数称作声强的声强级,记作
(贝尔),即.取贝尔的10倍作为响度的常用单位,简称为分贝,已知某处“喊泉”的声音强度
(分贝)与喷出的泉水高度
()之间满足关系式,甲?乙两名同学大喝一声激起的涌泉的最高高度分别为,.若甲同学大喝一声的声强大约相当于个乙同学同时大喝一声的声强,则的值约为(
)
A.10
B.100
C.200
D.1000
【例7】单位时间内通过道路上指定断面的车辆数被称为“道路容量”,与道路设施、交通服务、环境、气候等诸多条件相关.假设某条道路一小时通过的车辆数满足关系,其中为安全距离,为车速.当安全距离取时,该道路一小时“道路容量”的最大值约为(
)
A.135
B.149
C.165
D.195
【变式7.1】某工厂某种航空产品的年固定成本为万元,每生产件,需另投入成本为,当年产量不足件时,(万元).当年产量不小于件时,(万元).每件商品售价为万元.通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润(万元)关于年产量(件)的函数解析式;
(2)年产量为多少件时,该厂在这一商品的生产中所获利润最大?
.
课后作业:
一、选择题.
1.某食品的保鲜时间(单位:小时)与储藏温度(单位:)满足函数关系,且该食品在的保鲜时间是16小时,已知甲在某日上午10时购买了该食品,并将其遗放在室外,且此日的室外温度随时间变化如图所示,给出以下三个结论,其中,所有正确结论的个数是(
)
①该食品在的保鲜时间是8小时;
②当时,该食品的保鲜时间t随着x增大而减少;
③到了此日15时,甲所购买的食品还在保鲜时间内.
A.2
B.3
C.0
D.1
2.中国茶文化博大精深,茶水的口感与茶叶类型和水的温度有关.经验表明,某种绿茶用的水泡制,再等到茶水温度降至时饮用,可以产生最佳口感.为分析泡制一杯最佳口感茶水所需时间,某硏究人员每隔测量一次茶水的温度,根据所得数据做出如图所示的散点图.观察散点图的分布情况,下列哪个函数模型可以近似地刻画茶水温度随时间变化的规律(
)
A.
B.
C.
D.
3.在新冠肺炎疫情期间,某学校定期对教室进行药熏消毒.教室内每立方米空气中的含药量(单位:毫克)随时间(单位:小时)的变化情况如图所示.在药物释放的过程中,与成正比;药物释放完毕后,与的函数关系式为(为常数).据测定,当空气中每立方米的含药量降低到毫克以下时,学生方可进入教室.那么,从药物释放开始到学生能回到教室,至少在(
)(参考数值).
A.42分钟后
B.48分钟后
C.50分钟后
D.60分钟后
4.“百日冲刺”是各个学校针对高三学生进行的高考前的激情教育,它能在短时间内最大限度激发一个人的潜能,使成绩在原来的基础上有不同程度的提高,以便在高考中取得令人满意的成绩,特别对于成绩在中等偏下的学生来讲,其增加分数的空间尤其大.现有某班主任老师根据历年成绩在中等偏下的学生经历“百日冲刺”之后的成绩变化,构造了一个经过时间(单位:天),增加总分数(单位:分)的函数模型:,为增分转化系数,为“百日冲刺”前的最后一次模考总分,且.现有某学生在高考前天的最后一次模考总分为分,依据此模型估计此学生在高考中可能取得的总分约为(
)()
A.分
B.分
C.分
D.分
5.如图所示,液体从一个圆锥形漏斗漏入一个圆柱形桶中,开始时漏斗中盛满液体,经过3秒漏完,圆柱形桶中液面上升速度是一个常量,则漏斗中液面下降的高度H与下降时间t之间的函数关系的图象只可能是(
)
A.
B.C.
D.
6.“绿水青山就是金山银山”,党的十九大以来,城乡深化河道生态环境治理,科学治污.某乡村一条污染河道的蓄水量为立方米,每天的进出水量为立方米.已知污染源以每天个单位污染河水,某一时段(单位:天)河水污染质量指数为(每立方米河水所含的污染物)满足(为初始质量指数),经测算,河道蓄水量是每天进出水量的80倍.若从现在开始关闭污染源,要使河水的污染水平下降到初始时的10%,需要的时间大约是(参考数据:)(
)
A.1个月
B.3个月
C.半年
D.1年
二、解答题.
7.某民营企业开发出了一种新产品,预计能获得50万元到1500万元的经济收益.企业财务部门研究对开发该新产品的团队进行奖励,并讨论了一个奖励方案:奖金(单位:万元)随经济收益(单位:万元)的增加而增加,且,奖金金额不超过20万元.
(1)请你为该企业构建一个关于的函数模型,并说明你的函数模型符合企业奖励要求的理由;(答案不唯一)
(2)若该企业采用函数作为奖励函数模型,试确定实数的取值范围.
8.某科技公司生产某种芯片.由以往的经验表明,不考虑其他因素,该芯片每日的销售量y(单位:枚)与销售价格x(单位:元/枚,):当时满足关系式,(m,n为常数);当时满足关系式.已知当销售价格为20元/枚时,每日可售出该芯片7000枚;当销售价格为30元/枚时,每日可售出该芯片1500枚.
(1)求m,n的值,并确定y关于x的函数解析式;
(2)若该芯片的成本为10元/枚,试确定销售价格x的值,使公司每日销售该芯片所获利润最大.(x精确到元/枚)
9.经过考察,某公司打算对两个项目进行投资,经测算,投资项目(百万元)与产生的经济效益之间满足:(百万元),投资项目与产生的项目经济效益之间满足:(百万元).
(1)公司现有1200万资金可供投资,应如何分配资金使得投资收益总额最大;
(2)若投资百万元的某项目产生的经济效益为百万元,设投资该项目的边际效应函数为,其边际效应值小于0时,不建议投资该项目,那么对项目与应如何投资,才能使得经济效益最好?
10.某网店有(万件)商品,计划在元旦旺季售出商品x(万件),经市场调查测算,花费t(万元)进行促销后,商品的剩余量与促销费t之间的关系为(其中k为常数),如果不搞促销活动,只能售出1(万件)商品.
(1)要使促销后商品的剩余量不大于(万件),促销费t至少为多少(万元)?
(2)已知商品的进价为32(元/件),另有固定成本3(万元),定义每件售出商品的平均成本为(元),若将商品售价定位:“每件售出商品平均成本的倍”与“每件售出商品平均促销费的一半”之和,则当促销费t为多少(万元)时,该网店售出商品的总利润最大?此时商品的剩余量为多少?
11.上海某工厂以千克/小时的速度匀速生产某种产品,每一小时可获得的利润是元,其中.
(1)要使生产该产品2小时获得的利润不低于30元,求的取值范围;
(2)要使生产900千克该产品获得的利润最大,问:该厂应选取何种生产速度?并求最大利润.
1利用函数图像刻画实际问题
【例1】下面是一幅统计图,根据此图得到的以下说法中,正确的个数是(
)
①这几年生活水平逐年得到提高;
②生活费收入指数增长最快的一年是2014年;
③生活价格指数上涨速度最快的一年是2015年;
④虽然2016年生活费收入增长缓慢,但生活价格指数也略有降低,因而生活水平有较大的改善.
A.1
B.2
C.3
D.4
【答案】C
【解析】由图知,“生活费收入指数”减去“生活价格指数”的差是逐年增大的,故①正确;
“生活费收入指数”在2014~2015年最陡;故②正确;
“生活价格指数”在2015~2016年最平缓,故③不正确;
“生活价格指数”略呈下降,而“生活费收入指数”呈上升趋势,故④正确,
故选C.
【变式1.1】因市场战略储备的需要,某公司月日起,每月日购买了相同金额的某种物资,连续购买了次.由于市场变化,月日该公司不得不将此物资全部卖出.已知该物资的购买和卖出都是以份为计价单位进行交易,且该公司在买卖的过程中赢利,那么下面三个折线图中反映了这种物资每份价格(单位:万元)的可能变化情况是(
)
A.①
B.②
C.①②
D.①③
【答案】D
【解析】设公司每月日用于购买某种物资的金额为万元.
图①中四次购买的物资为(份),
月日一次卖出物资,公司得到,公司盈利,故①满足条件;
图②中四次购买的物资为(份),
月日一次卖出物资,公司得到,公司亏本,故②不满足条件;
图③中四次购买的物资为(份),
月日一次卖出物资,公司得到,公司盈利,故③满足条件,
故选D.
【例2】某医药研究所研发了一种治疗某疾病的新药,服药后,当每毫升血液中含药量不少于毫克时,治疗疾病有效.据监测,服药后每毫升血液中的含药量y(单位:毫克)与时间t(单位:时)之间满足如图所示的曲线,则服药一次后治疗疾病的有效时间为(
)
A.
B.
C.5
D.6
【答案】B
【解析】由题意,当时,函数图象是一个线段,
由于过原点与点,故其解析式为,;
当时,函数的解析式为,
此时在曲线上,将此点的坐标代入函数解析式得,解得,
故函数的解析式为,.
所以.
令,即,解得,
,
服药一次治疗疾病有效的时间为小时,故选B.
【变式2.1】(多选)如图,某池塘里浮萍的面积(单位:)与时间(单位:月)的关系为,关于下列说法正确的是(
)
A.浮萍每月的增长率为2
B.浮萍每月增加的面积都相等
C.第4个月时,浮萍面积超过
D.若浮萍蔓延到所经过的时间分别是,则
【答案】CD
【解析】由图可知,过,所以,,
对A,由为指数函数,为爆炸式增长,
取前三个月浮萍面积,,,故增长率逐月增大,故A错误;
对B,第一个月为,第二个月为,第三个月为,
浮萍每月增加的面积不相等,
对C,,,故C正确;
对D,,,,
所以,,
所以,故D正确,
故选CD.
【例3】水以恒速注入下图所示容器中,则水的高度与时间的函数关系是(
)
A.
B.
C.
D.
【答案】A
【解析】容器由下到上口径越来越大,水以恒速注入,则容器中水的高度增加的速度逐渐变慢,A符合;
B选项容器中水的高度增加的速度逐渐变快;
C选项容器中水的高度是匀速增加;
D选项容器中水的高度增加的速度先增加较慢,后增加较快,
故选A.
【变式3.1】如图,是边长为2的正三角形,记位于直线左侧的图形的面积为,则的函数图象是(
)
A.
B.C.
D.
【答案】A
【解析】根据题意,当时,;
当时,;
当时,,
所以只有A选项符合,故选A.
2函数模型解决实际问题
【例4】山东省寿光市绿色富硒产品和特色农产品在国际市场上颇具竞争力,其中香菇远销日本和韩国等地.上市时,外商李经理按市场价格元/千克在本市收购了千克香菇存放入冷库中.据预测,香菇的市场价格每天每千克将上涨元,但冷库存放这批香菇时每天需要支出各种费用合计元,而且香菇在冷库中最多保存天,同时,平均每天有千克的香菇损坏不能出售.
(1)若存放天后,将这批香菇一次性出售,设这批香菇的销售总金额为元,试写出与之间的函数关系式;
(2)李经理如果想获得利润元,需将这批香菇存放多少天后出售?(提示:利润=销售总金额-收购成本-各种费用)
(3)李经理将这批香菇存放多少天后出售可获得最大利润?最大利润是多少?
【答案】(1);(2)将这批香菇存放天后出售;(3)存放天后出售可获得最大利润为元.
【解析】(1)由题意得,与之间的函数关系式为:
.
(2)由题意得,
化简得,解得,(不合题意,舍去),
因此,李经理如果想获得利润元,需将这批香菇存放天后出售.
(3)设利润为,则由(2)得
,
因此当时,,
又因为,所以李经理将这批香菇存放天后出售可获得最大利润为元.
【变式4.1】在对口扶贫工作中,生态基地种植某中药材的年固定成本为250万元,每产出吨需另外投入可变成本万元,已知.通过市场分析,该中药材可以每吨50万元的价格全部售完.设基地种植该中药材年利润为万元,当基地产出该中药材40吨时,年利润为190万元.
(1)求的值;
(2)求年利润的最大值(精确到万元),并求此时的年产量(精确到吨).
【答案】(1);(2)当年产量约为吨时,年利润最大约为万元.
【解析】(1)由题意,当基地产出该中药材40吨时,年成本为万元,
利润为,解得.
(2)当时,利润为,
因为对称轴,在上为增函数,
所以当时,万元;
当时,,
,
当且仅当,即时取等号,
所以当年产量约为吨时,年利润最大约为万元.
【例5】基本再生数R0与世代间隔T是新冠肺炎的流行病学基本参数.基本再生数指一个感染者传染的平均人数,世代间隔指相邻两代间传染所需的平均时间.在新冠肺炎疫情初始阶段,可以用指数模型:描述累计感染病例数I(t)随时间t(单位:天)的变化规律,指数增长率r与R0,T近似满足.有学者基于已有数据估计出,.据此,在新冠肺炎疫情初始阶段,累计感染病例数增加3倍需要的时间约为(
)
A.天
B.天
C.天
D.天
【答案】D
【解析】把,代入,可得,
,
当时,,则,
两边取对数得,解得,故选D.
【变式5.1】“一骑红尘妃子笑,无人知是荔枝来”描述了封建统治者的骄奢生活,同时也讲述了古代资源流通的不便利.如今我国物流行业蓬勃发展,极大地促进了社会经济发展和资源整合.已知某类果蔬的保鲜时间y(单位:小时)与储藏温度x(单位:)满足函数关系(a,b为常数),若该果蔬在的保鲜时间为216小时,在的保鲜时间为8小时,那么在时,该果蔬的保鲜时间为(
)小时.
A.72
B.36
C.24
D.16
【答案】A
【解析】当时,;当时,,
则,整理可得,于是,
当时,,
故选A.
【例6】核酸检测分析是用荧光定量法,通过化学物质的荧光信号,对在扩增进程中成指数级增加的靶标实时监测,在扩增的指数时期,荧光信号强度达到阈值时,的数量与扩增次数满足,其中为扩增效率,为的初始数量.已知某被测标本扩增次后,数量变为原来的倍,那么该样本的扩增效率约为(
)
(参考数据:,)
A.
B.
C.
D.
【答案】C
【解析】由题意知,,
即,
所以,解得,
故选C.
【变式6.1】“喊泉”是一种地下水的毛细现象,人们在泉口吼叫或发出其他声音时,声波传入泉洞内的储水池,进而产生“共鸣”等作用,激起水波,形成涌泉,声音越大,涌起的泉水越高.已知听到的声强与标准声强
(约为,单位:)之比的常用对数称作声强的声强级,记作
(贝尔),即.取贝尔的10倍作为响度的常用单位,简称为分贝,已知某处“喊泉”的声音强度
(分贝)与喷出的泉水高度
()之间满足关系式,甲?乙两名同学大喝一声激起的涌泉的最高高度分别为,.若甲同学大喝一声的声强大约相当于个乙同学同时大喝一声的声强,则的值约为(
)
A.10
B.100
C.200
D.1000
【答案】B
【解析】设甲同学的声强为,乙同学的声强为,则,,
两式相减即得,即从而,所以的值约为100,
故选B.
【例7】单位时间内通过道路上指定断面的车辆数被称为“道路容量”,与道路设施、交通服务、环境、气候等诸多条件相关.假设某条道路一小时通过的车辆数满足关系,其中为安全距离,为车速.当安全距离取时,该道路一小时“道路容量”的最大值约为(
)
A.135
B.149
C.165
D.195
【答案】B
【解析】由题意得,,
当且仅当,即时取“=”,
所以该道路一小时“道路容量”的最大值约为149,故选B.
【变式7.1】某工厂某种航空产品的年固定成本为万元,每生产件,需另投入成本为,当年产量不足件时,(万元).当年产量不小于件时,(万元).每件商品售价为万元.通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润(万元)关于年产量(件)的函数解析式;
(2)年产量为多少件时,该厂在这一商品的生产中所获利润最大?
【答案】(1);(2)年产量为件时,利润最大为万元.
【解析】(1)当时,;
当时,,
所以.
(2)当时,,
此时,当时,取得最大值万元.
当时,,
此时,当时,即时,取得最大值万元,,
所以年产量为件时,利润最大为万元.
课后作业:
一、选择题.
1.某食品的保鲜时间(单位:小时)与储藏温度(单位:)满足函数关系,且该食品在的保鲜时间是16小时,已知甲在某日上午10时购买了该食品,并将其遗放在室外,且此日的室外温度随时间变化如图所示,给出以下三个结论,其中,所有正确结论的个数是(
)
①该食品在的保鲜时间是8小时;
②当时,该食品的保鲜时间t随着x增大而减少;
③到了此日15时,甲所购买的食品还在保鲜时间内.
A.2
B.3
C.0
D.1
【答案】A
【解析】由题意可得,当时,保鲜时间是16小时,即,解得,
①当时,,故保鲜时间是8小时,故①正确;
②当时,为减函数,则该食品的保鲜时间t随着x增大而减少,故②正确;
③在某日上午10时,温度为8度,此时保鲜时间为小时,到了此日15时,已经过了保鲜时间,所以甲所购买的食品不在保鲜时间内,故③不正确,
故选A.
2.中国茶文化博大精深,茶水的口感与茶叶类型和水的温度有关.经验表明,某种绿茶用的水泡制,再等到茶水温度降至时饮用,可以产生最佳口感.为分析泡制一杯最佳口感茶水所需时间,某硏究人员每隔测量一次茶水的温度,根据所得数据做出如图所示的散点图.观察散点图的分布情况,下列哪个函数模型可以近似地刻画茶水温度随时间变化的规律(
)
A.
B.
C.
D.
【答案】B
【解析】由函数图象可知符合条件的只有指数函数模型,并且,,
故选B.
3.在新冠肺炎疫情期间,某学校定期对教室进行药熏消毒.教室内每立方米空气中的含药量(单位:毫克)随时间(单位:小时)的变化情况如图所示.在药物释放的过程中,与成正比;药物释放完毕后,与的函数关系式为(为常数).据测定,当空气中每立方米的含药量降低到毫克以下时,学生方可进入教室.那么,从药物释放开始到学生能回到教室,至少在(
)(参考数值).
A.42分钟后
B.48分钟后
C.50分钟后
D.60分钟后
【答案】B
【解析】把点代入中,,解得.
所以当时,,
因为当空气中每立方米的含药量降低到毫克以下时,学生方可进入教室,
所以,解得.
至少需要经过分钟后,学生才能回到教室,
故选B.
4.“百日冲刺”是各个学校针对高三学生进行的高考前的激情教育,它能在短时间内最大限度激发一个人的潜能,使成绩在原来的基础上有不同程度的提高,以便在高考中取得令人满意的成绩,特别对于成绩在中等偏下的学生来讲,其增加分数的空间尤其大.现有某班主任老师根据历年成绩在中等偏下的学生经历“百日冲刺”之后的成绩变化,构造了一个经过时间(单位:天),增加总分数(单位:分)的函数模型:,为增分转化系数,为“百日冲刺”前的最后一次模考总分,且.现有某学生在高考前天的最后一次模考总分为分,依据此模型估计此学生在高考中可能取得的总分约为(
)()
A.分
B.分
C.分
D.分
【答案】B
【解析】由题意得:,,
,
该学生在高考中可能取得的总分约为分,故选B.
5.如图所示,液体从一个圆锥形漏斗漏入一个圆柱形桶中,开始时漏斗中盛满液体,经过3秒漏完,圆柱形桶中液面上升速度是一个常量,则漏斗中液面下降的高度H与下降时间t之间的函数关系的图象只可能是(
)
A.
B.C.
D.
【答案】B
【解析】由于所给的圆锥形漏斗上口大于下口,
当时间取时,漏斗中液面下落的高度不会达到漏斗高度的,
对比四个选项的图象可得结果,故选B.
6.“绿水青山就是金山银山”,党的十九大以来,城乡深化河道生态环境治理,科学治污.某乡村一条污染河道的蓄水量为立方米,每天的进出水量为立方米.已知污染源以每天个单位污染河水,某一时段(单位:天)河水污染质量指数为(每立方米河水所含的污染物)满足(为初始质量指数),经测算,河道蓄水量是每天进出水量的80倍.若从现在开始关闭污染源,要使河水的污染水平下降到初始时的10%,需要的时间大约是(参考数据:)(
)
A.1个月
B.3个月
C.半年
D.1年
【答案】C
【解析】由题可知:,∴,
∴,∴(天),
∴要使河水的污染水平下降到初始时的10%,需要的时间大约是半年,
故选C.
二、解答题.
7.某民营企业开发出了一种新产品,预计能获得50万元到1500万元的经济收益.企业财务部门研究对开发该新产品的团队进行奖励,并讨论了一个奖励方案:奖金(单位:万元)随经济收益(单位:万元)的增加而增加,且,奖金金额不超过20万元.
(1)请你为该企业构建一个关于的函数模型,并说明你的函数模型符合企业奖励要求的理由;(答案不唯一)
(2)若该企业采用函数作为奖励函数模型,试确定实数的取值范围.
【答案】(1)答案见解析;(2).
【解析】(1)答案不唯一.构造出一个函数;说明是单调增函数;函数的取值满足要求.
如,,就是符合企业奖励的一个函数模型.
理由:
根据一次函数的性质,易知,随增大而增大,即为增函数;
当时,,
当时,,即奖金金额且不超过20万元.
故该函数是符合企业奖励要求的一个函数模型.
(2)当时,易知是增函数,且当时,,当时,,即满足奖金且不超过20万的要求;
故当时,符合企业奖励要求.
当时,函数是增函数,即对任意,且时,成立.
故当且仅当,即时,此时函数在上是增函数.
由,得;进一步可知,,故成立,即当时,函数符合奖金且金额不超过20万的要求.
依据函数模型是符合企业的奖励要求,即此函数为增函数,
于是,有,解得,
综上,所求实数的取值范围是.
8.某科技公司生产某种芯片.由以往的经验表明,不考虑其他因素,该芯片每日的销售量y(单位:枚)与销售价格x(单位:元/枚,):当时满足关系式,(m,n为常数);当时满足关系式.已知当销售价格为20元/枚时,每日可售出该芯片7000枚;当销售价格为30元/枚时,每日可售出该芯片1500枚.
(1)求m,n的值,并确定y关于x的函数解析式;
(2)若该芯片的成本为10元/枚,试确定销售价格x的值,使公司每日销售该芯片所获利润最大.(x精确到元/枚)
【答案】(1),,;(2).
【解析】(1)因为时,;时,,
所以,解得,,
每日的销售量.
(2)由(1)知,当时:每日销售利润
,.
则,
当或时,,
当时,,单调递增;
当时,,单调递减,
是函数在上的唯一极大值点,;
当时:每日销售利润,
在有最大值,且.
综上,销售价格元/枚时,每日利润最大.
9.经过考察,某公司打算对两个项目进行投资,经测算,投资项目(百万元)与产生的经济效益之间满足:(百万元),投资项目与产生的项目经济效益之间满足:(百万元).
(1)公司现有1200万资金可供投资,应如何分配资金使得投资收益总额最大;
(2)若投资百万元的某项目产生的经济效益为百万元,设投资该项目的边际效应函数为,其边际效应值小于0时,不建议投资该项目,那么对项目与应如何投资,才能使得经济效益最好?
【答案】(1)A、B项目各6百万,收益最大为3400万;(2)A、B项目各550万.
【解析】(1)投资项目(百万元),则投资项目(百万元),
投资收益总额
,时取最大值,
即投资项目6百万,投资项目6百万,收益总额最大为万元.
(2)若投资项目(百万元),则,解得,
投资项目万元;
若投资项目(百万元),则,
解得,
应投资项目万元,
即两个项目各投资550万元时,经济效益最好.
10.某网店有(万件)商品,计划在元旦旺季售出商品x(万件),经市场调查测算,花费t(万元)进行促销后,商品的剩余量与促销费t之间的关系为(其中k为常数),如果不搞促销活动,只能售出1(万件)商品.
(1)要使促销后商品的剩余量不大于(万件),促销费t至少为多少(万元)?
(2)已知商品的进价为32(元/件),另有固定成本3(万元),定义每件售出商品的平均成本为(元),若将商品售价定位:“每件售出商品平均成本的倍”与“每件售出商品平均促销费的一半”之和,则当促销费t为多少(万元)时,该网店售出商品的总利润最大?此时商品的剩余量为多少?
【答案】(1)(万元);(2)当促销费为7万元时,网店利润的最大为42万元,此时商品的剩余量为(万件).
【解析】(1)由,当时,,得,∴,
由,解得,
所以促销费至少为19万元.
(2)网店的利润y(万元),
由题意可得
,
当且仅当,即时取等号,此时,
所以当促销费为7万元时,网店利润的最大为42万元,此时商品的剩余量为
(万件).
11.上海某工厂以千克/小时的速度匀速生产某种产品,每一小时可获得的利润是元,其中.
(1)要使生产该产品2小时获得的利润不低于30元,求的取值范围;
(2)要使生产900千克该产品获得的利润最大,问:该厂应选取何种生产速度?并求最大利润.
【答案】(1);(2),4575元.
【解析】(1),即,
整理可得,解得或
(舍去),
所以.
(2)要使生产900千克该产品获得的利润最大时为y,
,
,所以当,取最大值为4575元.
2
同课章节目录
