高中函数综合复习
图片预览





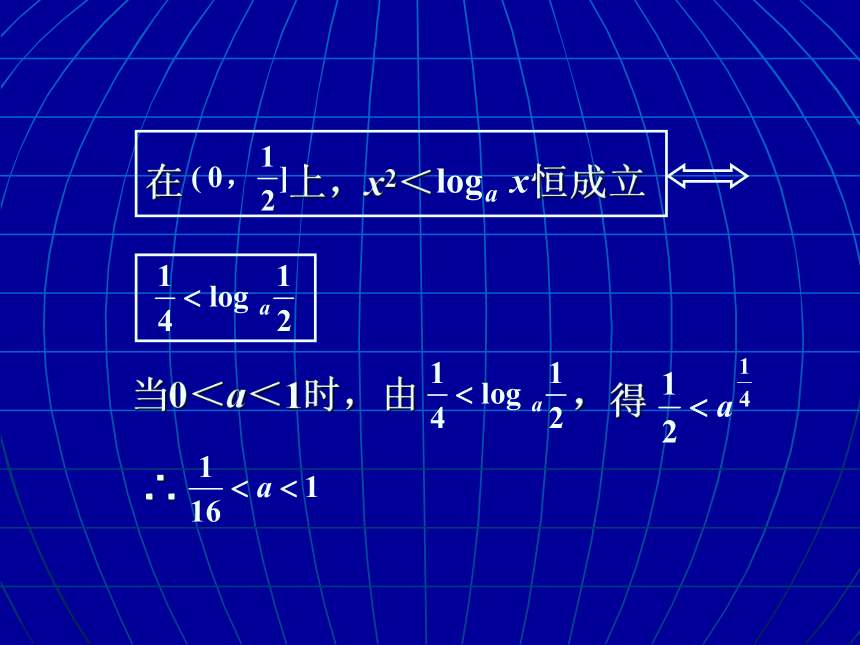


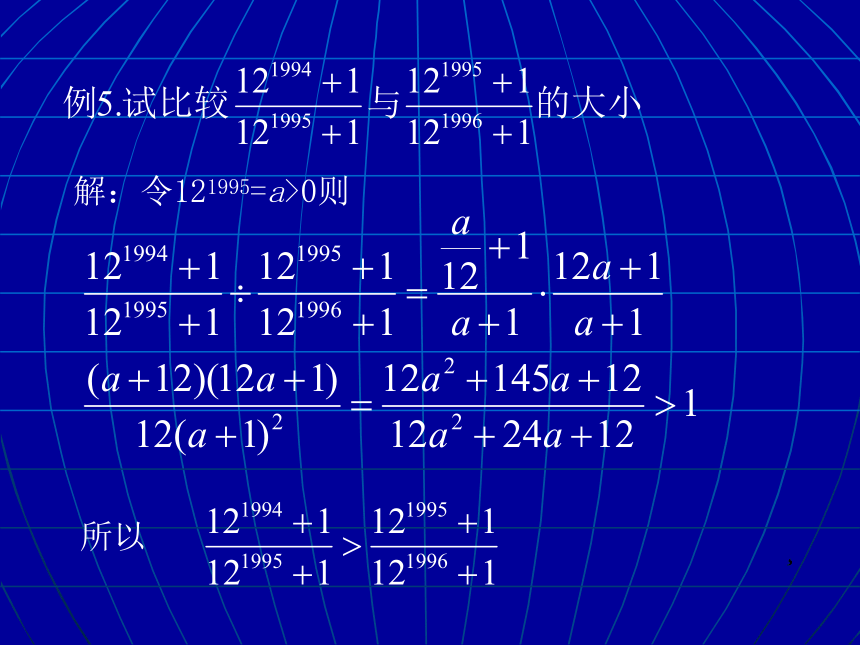

文档简介
(共60张PPT)
函数(三)
例1 已知函数 (a >0 且a ≠1) 在其定义域 [-1, 1] 上是减函数,则实数 a 的取值范围是___________.
六、幂函数、指数函数与对数函数
【讲解】由a>0且a≠1知t=3-ax是减函数,从而lg(3-ax) 也是减函数,故只有a>1时,f (x)才是减函数;
另外, x [-1 ,1] 时, 要保证 3-ax>0,为此只须考虑最小值:
x=1时, tmin=3-a,要3-a>0,
则a<3,综上知1<a<3.
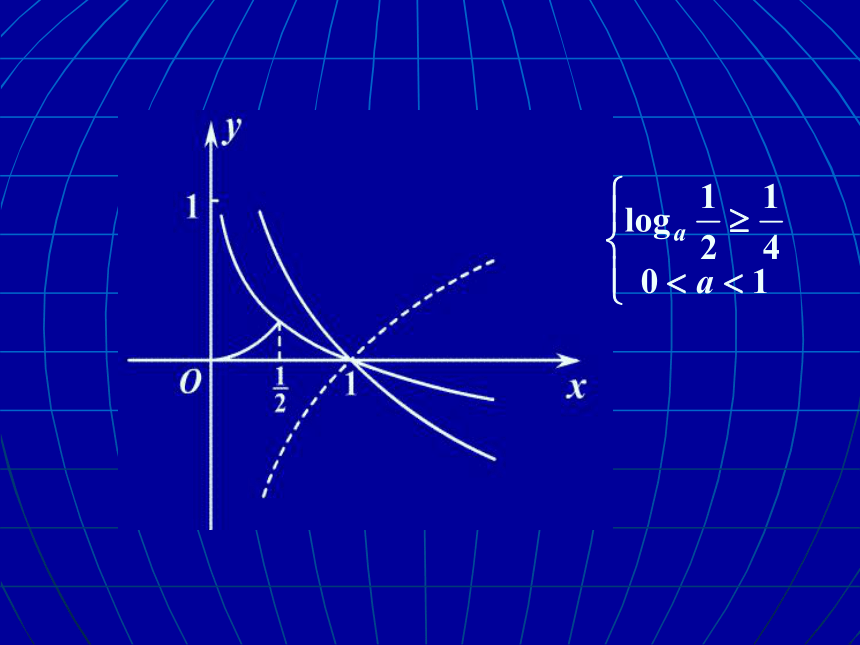
例2 如果不等式 x2- <0
在区间 上恒成立,那么实数a
的取值范围是___________.
【讲解】 设y=x2 ①
y= ②
当a>1时,函数②在 上取负值, 因此 不可能有x2< 成立.
在 上函数①的最大值是 ,
在 上,当0<a<1时,②的最小
值是 ,
在 上,x2< 恒成立
当0<a<1时,由 ,
得
∴
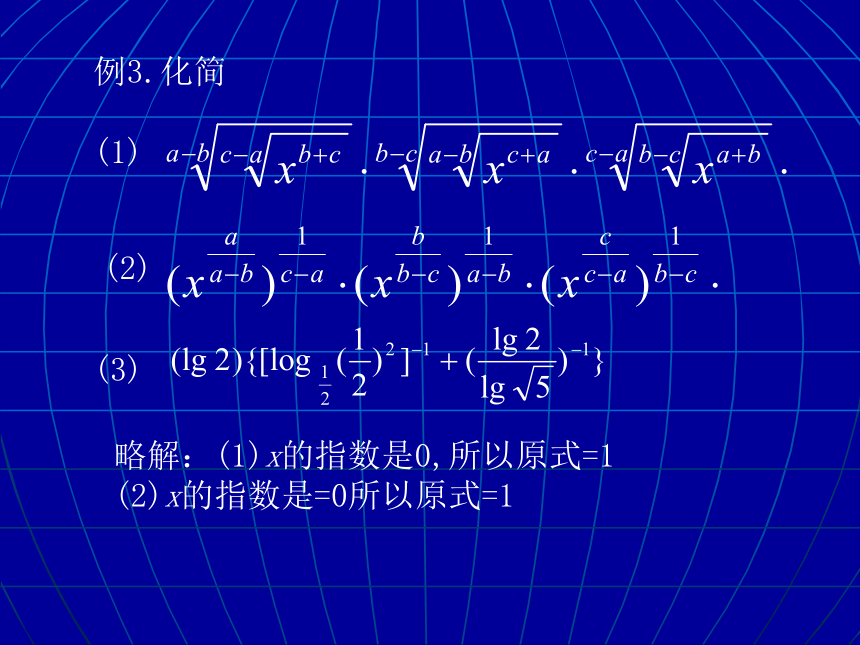
例3.化简
(1)
(2)
(3)
略解:(1)x的指数是0,所以原式=1
(2)x的指数是=0所以原式=1
(3)原式=
例4.若
,求
解:因为
所以f(x)+f(1-x)=1
解:令121995=a>0则
所以
例6.已知函数f(x)=logax (a>0,a≠1,x∈R+)若
x1,x2∈R+,试比较
与
的大小
例7.已知y1=
,y2=
当x为何值时
(1)y1=y2 (2)y1>y2 (3)y1例8.对于自然数a,b,c (a≤b≤c)和实数x,y,z,w若
(1)ax=by=cz=70w (2)
求证:a+b=c
例9.已知A=6lgp+lgq,其中p,q为素数,且满足
q-p=29,求证:3证明:由于p、q为素数,其差q-p=29为奇数,∴p=2,q=31
A=6lg2+lg31=lg(64×31)=lg1984
1000<1984<10000 故3例10.设f(x)=logax (a>0,a≠1)且
(θ为锐角),求证:1证明:∵θ是锐角,∴
从而a>1又f(15)=
=sinθ+cosθ
故a<15 综合得:1证:因为00,ay>0由平均值不等式
故
例11.已知0解:在直角坐标系内分别作出函数y=2x和y=log2x的图象,再作直线y=x和y= -x+3,由于y=2x和y=log2x互为反函数,故它们的图象关于直线y=x对称,方程log2x+x-3=0的根a就是直线y= -x+3与对数曲线y=log2x的交点A的横坐标,方程2x+x-3=0的根b就是直线y= -x+3与指数曲线y=2x的交点B的横坐标
设y= -x+3与y=x的交点为M,则点M的横坐标为(1.5,1.5),所以a+b=2xM=3 log2a+2b=2yM=3
例12.设a、b分别是方程log2x+x-3=0和2x+x-3=0的根,求a+b及log2a+2b
例13 已知函数 f (x)=|2x -1 -1 |, a<b<c 且 f (a)>f (c)>f (b) ,则必有
(A) a<b,b<1,c<1
(B) a<1,b≥1,c>1
(C) 2-a< 2c
(D) 2a+2c<4.
【解】函数y=2x的图像右移1个单位得 y = 2x-1 ,再下移1个单位得y = 2x-1 -1,再把 x 轴下方的部分翻折到x 轴上方得y =| 2x-1-1|,图像如下图
由于在 上,f (x) 是减函数,所 以 a, b,c 不能同时在 上;同理,a,b,c 也不能同时在 上.
故必有a<1且c>1.
从而2a-1<1,2c-1>1
∴ f (a)=1-2a-1,f (c)=2c-1-1
∵ f (a) >f (c)
∴ 1-2a-1>2c-1-1
∴ 2a+2c<4.
故选(D).
例14 设 m R,关于x 的方程
(a>0且a≠1) 有几个实根?证明你的结论.
【解】设y=ax,则y>0,且
(y + m)(y2+my+1) = 0
∴ y =-m ① 或y2+my+1=0 ②
令 , 则m≤-2
(1) 当m<-2 时,
① 有正实根,②有两个不等正实根.
∴ 原方程有三个实根;
(2) 当m=-2 时,
① 有正实根,②有一个正实根.
∴ 原方程有两个实根;
(3) 当-2<m<0 时,
① 有正实根,②无实根.
∴ 原方程有一个实根;
(4) 当m≥0 时,
① 只有负根,而②无实根或实根为负.
∴ 原方程无实根.
综上所述,知
m的值 m<-2 -2 -2<m<0 m≥0
方程实根个数 3 2 1 0
例15.解方程
(1)x+log2(2x-31)=5
(2) 2lgx×xlg2-3×xlg2-21+lgx+4=0
例16.设a>0且a≠1,求证:方程ax+a-x=2a的根不在区间[-1,1]内
解:设t=ax,则原方程化为:t2-2at+1=0 (1)
由Δ=4a2-4>0得a2>1,即a>1
令f(t)= t2-2at+1 , f(a)=a2-2a2+1=1-a2<0
下略
例16.解方程:lg2x-[lgx]-2=0 (其中[x]表示不大于实数x的最大整数)
解:由[x]的定义知,[x]≤x,
故原方程可变为不等式:
lg2x-lgx-2≤0即-1≤lgx≤2
当-1≤lgx<0时,[lgx]= -1,于是原方程为lg2x=1
当0≤lgx<1时,[lgx]=0,原方程为
lg2x=2,
均不符合[lgx]=0
当1≤lgx<2时,[lgx]=1,原方程为
lg2x=3,所以
当lgx=2时,x=100
所以原方程的解为
解:易知:a>0且a≠1,
设u=x2+ax+5,原不等式可化为
例18.当a为何值时,不等式
有且只有一解
因为f(4)=log3(2+1)×log5(4+1)=1
所以(1)等价于u>4,即x2+ax+5>4
此不等式有无穷多解
(1)当0(1)
由于当u>0时,
均为单调增函数,所以它们的乘积
也是单增函数
由f(4)=1知,(2)等价于0≤u≤4,
即0≤x2+ax+5≤4
从上式可知,只有当x2+ax+5=4有唯一解
即Δ=a2-4=0,a=2时,
不等式0≤x2+ax+5≤4有唯一解x= -1
综上所述,当a=2时原不等式有且只有一个解
(2)当a>1时,不等式化为
(2)
例19.已知a>0且a≠1,试求使方程
有解的k的取值范围
解:原方程即
即
又当k=0时,代入原式可推出a=0与已知矛盾,
故k的取值范围为(-∞,-1)U(0,1)
分别解关于 的不等式、方程得:
(k≠0时)
所以
解得k< -1或0解:易知f(x)的定义域为(0,+∞)
∵y1=3+ 在(0,+∞)上是减函数,
y2=log2x在(0,+∞)上是增函数,
而当y1=y2,即
例20.设f(x)=min(3+ , ),其中min(p,q)表
示p、q中的较小者,求f(x)的最大值
七.函数的最值与函数的值域
f(x)=log2x (2)
(1)×2+(2)消去log2x,
得3f(x)=6,f(x)=2
又f(4)=2,故f(x)的最大值为2
另解:f(x)=3+ =3- (1)
3+ =log2x时,x=4,
故当x=4时,得f(x)的最大值是2
例21.求函数
的最小值
解:由1-3x>0得,x<0,所以函数的定义域为(-∞,0)
令3x=t,则t∈(0,1),于是
故当x= -1时,得y的最小值-2+2log23
例22 已知函数f (x) 和g(x)都是奇函数,且 F(x) =a · f (x)+b · g(x)+2 ,若在 (0, +∞)上F(x)有最大值8, 则在(-∞, 0)上F(x) 有
(A) 最小值-8 (B) 最小值-4
(C) 最小值-6 (D) 最大值-8
【解】设x<0,则-x>0,
依题意F(-x)=af (-x)+bg(-x)+2≤8
∵ f (x) 和g(x)是奇函数
∴-af (x)-bg (x)+2≤8
∴ a · f (x)+bg (x)≥-6
∴ F (x)=af (x)+bg (x)+2≥-4.
故F (x)在(-∞,0)上有最小值-4.
应选(B).
例23 求函数 的值域.
【讲解】 和 这两项的平方和是常数,而平方之积是二次三项式.
据这个特点可以演变出下面多种解法.
【解法1】易知定义域为 0≤x≤1,
0≤x≤1 -x2+x 的值域是 [0, ]
的值域是 [0, ]
∴ 的值域是[1, ].
∵
≤1+x-x+1
=2
∴ 且 时,
等号成立.
【解法2】
又由0≤x≤1知x2≤x , ∴
, ∴
且x=1或0 时等号成立.
综合以上结果知, 的值域是 [1, ].
【解法3】 设 , t [0,1]
则
整理,得2t 2-2yt + y 2 -1=0
由于该方程有非负实根,
所以
解之,得 .
当y=1时x=1或0,
时,
故两个等号皆成立,故值域为
【解法4】 ∵
且
∴ 设 ,
则 .
∵ ∴
∴ ∴值域为[1, ].
例24 已知函数 , 定义域为 , 且a<b,求函数的最小值.
【讲解】若把定义域扩大为 ,那么用平均值不等式知,x=b时,y 有最小值2b, 而当 时, ,于是猜想,在 上函数递减,当然在 上也是减函数.于是有下面的解法1和2.
∵ 0<x≤a<b
∴ a · x-b2<0 且 x-a<0
∴ .且 x=a 时,
等号成立.故y 的最小值为 .
【解法1】
【解法2】 令0<x1<x2≤a<b,
则x1-x2<0 且x1 · x2<b2,
f (x1)-f (x2)=(x1-x2)
∴ f (x1) > f (x2)
即 f (x) 在 上是减函数,
∴ x=a 时,y 最小且 .
【讲解】另一个途径就是对函数解析式做出变形,一方面可以变换为x的一元二次方程,用根的判别式建立y的不等式,另一方面可以创造条件使用均值不等式,或配方,以构造y的不等式,另外,函数解析式变形后,可以和三角公式相联系,寻求三角代换的方法.
【讲解3】 函数式化为
x2-yx + b2=0
依题意,该方程在 上有实根,于是
△= y2-4b2≥0,即y≥2b.
而函数 (x)=x2-yx+b2图像的对称轴为
.
因此,函数 (x) 在 上递减,故只能有一个实根,该实根存在的充要条件是 (a) ≤0
即a2-ay + b2≤0,
y≥ 且x=a 时,等式成立,
故 .
∵ ,x=a 时等号成立,
而 在 上是减函数, x=a 时,
其值最小,
故x=a 时, y 有最小值, .
【解法4】
【解法5】
由0<x≤a<b 得
且b-x≥b-a>0
∴
∴
当x=a 时, .
【解法6】
令 = tan ,
∵ 0<x≤a<b , ∴
∴ .
且 时, .
即
函数(三)
例1 已知函数 (a >0 且a ≠1) 在其定义域 [-1, 1] 上是减函数,则实数 a 的取值范围是___________.
六、幂函数、指数函数与对数函数
【讲解】由a>0且a≠1知t=3-ax是减函数,从而lg(3-ax) 也是减函数,故只有a>1时,f (x)才是减函数;
另外, x [-1 ,1] 时, 要保证 3-ax>0,为此只须考虑最小值:
x=1时, tmin=3-a,要3-a>0,
则a<3,综上知1<a<3.
例2 如果不等式 x2- <0
在区间 上恒成立,那么实数a
的取值范围是___________.
【讲解】 设y=x2 ①
y= ②
当a>1时,函数②在 上取负值, 因此 不可能有x2< 成立.
在 上函数①的最大值是 ,
在 上,当0<a<1时,②的最小
值是 ,
在 上,x2< 恒成立
当0<a<1时,由 ,
得
∴
例3.化简
(1)
(2)
(3)
略解:(1)x的指数是0,所以原式=1
(2)x的指数是=0所以原式=1
(3)原式=
例4.若
,求
解:因为
所以f(x)+f(1-x)=1
解:令121995=a>0则
所以
例6.已知函数f(x)=logax (a>0,a≠1,x∈R+)若
x1,x2∈R+,试比较
与
的大小
例7.已知y1=
,y2=
当x为何值时
(1)y1=y2 (2)y1>y2 (3)y1
(1)ax=by=cz=70w (2)
求证:a+b=c
例9.已知A=6lgp+lgq,其中p,q为素数,且满足
q-p=29,求证:3
A=6lg2+lg31=lg(64×31)=lg1984
1000<1984<10000 故3
(θ为锐角),求证:1
从而a>1又f(15)=
=sinθ+cosθ
故a<15 综合得:1
故
例11.已知0
设y= -x+3与y=x的交点为M,则点M的横坐标为(1.5,1.5),所以a+b=2xM=3 log2a+2b=2yM=3
例12.设a、b分别是方程log2x+x-3=0和2x+x-3=0的根,求a+b及log2a+2b
例13 已知函数 f (x)=|2x -1 -1 |, a<b<c 且 f (a)>f (c)>f (b) ,则必有
(A) a<b,b<1,c<1
(B) a<1,b≥1,c>1
(C) 2-a< 2c
(D) 2a+2c<4.
【解】函数y=2x的图像右移1个单位得 y = 2x-1 ,再下移1个单位得y = 2x-1 -1,再把 x 轴下方的部分翻折到x 轴上方得y =| 2x-1-1|,图像如下图
由于在 上,f (x) 是减函数,所 以 a, b,c 不能同时在 上;同理,a,b,c 也不能同时在 上.
故必有a<1且c>1.
从而2a-1<1,2c-1>1
∴ f (a)=1-2a-1,f (c)=2c-1-1
∵ f (a) >f (c)
∴ 1-2a-1>2c-1-1
∴ 2a+2c<4.
故选(D).
例14 设 m R,关于x 的方程
(a>0且a≠1) 有几个实根?证明你的结论.
【解】设y=ax,则y>0,且
(y + m)(y2+my+1) = 0
∴ y =-m ① 或y2+my+1=0 ②
令 , 则m≤-2
(1) 当m<-2 时,
① 有正实根,②有两个不等正实根.
∴ 原方程有三个实根;
(2) 当m=-2 时,
① 有正实根,②有一个正实根.
∴ 原方程有两个实根;
(3) 当-2<m<0 时,
① 有正实根,②无实根.
∴ 原方程有一个实根;
(4) 当m≥0 时,
① 只有负根,而②无实根或实根为负.
∴ 原方程无实根.
综上所述,知
m的值 m<-2 -2 -2<m<0 m≥0
方程实根个数 3 2 1 0
例15.解方程
(1)x+log2(2x-31)=5
(2) 2lgx×xlg2-3×xlg2-21+lgx+4=0
例16.设a>0且a≠1,求证:方程ax+a-x=2a的根不在区间[-1,1]内
解:设t=ax,则原方程化为:t2-2at+1=0 (1)
由Δ=4a2-4>0得a2>1,即a>1
令f(t)= t2-2at+1 , f(a)=a2-2a2+1=1-a2<0
下略
例16.解方程:lg2x-[lgx]-2=0 (其中[x]表示不大于实数x的最大整数)
解:由[x]的定义知,[x]≤x,
故原方程可变为不等式:
lg2x-lgx-2≤0即-1≤lgx≤2
当-1≤lgx<0时,[lgx]= -1,于是原方程为lg2x=1
当0≤lgx<1时,[lgx]=0,原方程为
lg2x=2,
均不符合[lgx]=0
当1≤lgx<2时,[lgx]=1,原方程为
lg2x=3,所以
当lgx=2时,x=100
所以原方程的解为
解:易知:a>0且a≠1,
设u=x2+ax+5,原不等式可化为
例18.当a为何值时,不等式
有且只有一解
因为f(4)=log3(2+1)×log5(4+1)=1
所以(1)等价于u>4,即x2+ax+5>4
此不等式有无穷多解
(1)当0
由于当u>0时,
均为单调增函数,所以它们的乘积
也是单增函数
由f(4)=1知,(2)等价于0≤u≤4,
即0≤x2+ax+5≤4
从上式可知,只有当x2+ax+5=4有唯一解
即Δ=a2-4=0,a=2时,
不等式0≤x2+ax+5≤4有唯一解x= -1
综上所述,当a=2时原不等式有且只有一个解
(2)当a>1时,不等式化为
(2)
例19.已知a>0且a≠1,试求使方程
有解的k的取值范围
解:原方程即
即
又当k=0时,代入原式可推出a=0与已知矛盾,
故k的取值范围为(-∞,-1)U(0,1)
分别解关于 的不等式、方程得:
(k≠0时)
所以
解得k< -1或0
∵y1=3+ 在(0,+∞)上是减函数,
y2=log2x在(0,+∞)上是增函数,
而当y1=y2,即
例20.设f(x)=min(3+ , ),其中min(p,q)表
示p、q中的较小者,求f(x)的最大值
七.函数的最值与函数的值域
f(x)=log2x (2)
(1)×2+(2)消去log2x,
得3f(x)=6,f(x)=2
又f(4)=2,故f(x)的最大值为2
另解:f(x)=3+ =3- (1)
3+ =log2x时,x=4,
故当x=4时,得f(x)的最大值是2
例21.求函数
的最小值
解:由1-3x>0得,x<0,所以函数的定义域为(-∞,0)
令3x=t,则t∈(0,1),于是
故当x= -1时,得y的最小值-2+2log23
例22 已知函数f (x) 和g(x)都是奇函数,且 F(x) =a · f (x)+b · g(x)+2 ,若在 (0, +∞)上F(x)有最大值8, 则在(-∞, 0)上F(x) 有
(A) 最小值-8 (B) 最小值-4
(C) 最小值-6 (D) 最大值-8
【解】设x<0,则-x>0,
依题意F(-x)=af (-x)+bg(-x)+2≤8
∵ f (x) 和g(x)是奇函数
∴-af (x)-bg (x)+2≤8
∴ a · f (x)+bg (x)≥-6
∴ F (x)=af (x)+bg (x)+2≥-4.
故F (x)在(-∞,0)上有最小值-4.
应选(B).
例23 求函数 的值域.
【讲解】 和 这两项的平方和是常数,而平方之积是二次三项式.
据这个特点可以演变出下面多种解法.
【解法1】易知定义域为 0≤x≤1,
0≤x≤1 -x2+x 的值域是 [0, ]
的值域是 [0, ]
∴ 的值域是[1, ].
∵
≤1+x-x+1
=2
∴ 且 时,
等号成立.
【解法2】
又由0≤x≤1知x2≤x , ∴
, ∴
且x=1或0 时等号成立.
综合以上结果知, 的值域是 [1, ].
【解法3】 设 , t [0,1]
则
整理,得2t 2-2yt + y 2 -1=0
由于该方程有非负实根,
所以
解之,得 .
当y=1时x=1或0,
时,
故两个等号皆成立,故值域为
【解法4】 ∵
且
∴ 设 ,
则 .
∵ ∴
∴ ∴值域为[1, ].
例24 已知函数 , 定义域为 , 且a<b,求函数的最小值.
【讲解】若把定义域扩大为 ,那么用平均值不等式知,x=b时,y 有最小值2b, 而当 时, ,于是猜想,在 上函数递减,当然在 上也是减函数.于是有下面的解法1和2.
∵ 0<x≤a<b
∴ a · x-b2<0 且 x-a<0
∴ .且 x=a 时,
等号成立.故y 的最小值为 .
【解法1】
【解法2】 令0<x1<x2≤a<b,
则x1-x2<0 且x1 · x2<b2,
f (x1)-f (x2)=(x1-x2)
∴ f (x1) > f (x2)
即 f (x) 在 上是减函数,
∴ x=a 时,y 最小且 .
【讲解】另一个途径就是对函数解析式做出变形,一方面可以变换为x的一元二次方程,用根的判别式建立y的不等式,另一方面可以创造条件使用均值不等式,或配方,以构造y的不等式,另外,函数解析式变形后,可以和三角公式相联系,寻求三角代换的方法.
【讲解3】 函数式化为
x2-yx + b2=0
依题意,该方程在 上有实根,于是
△= y2-4b2≥0,即y≥2b.
而函数 (x)=x2-yx+b2图像的对称轴为
.
因此,函数 (x) 在 上递减,故只能有一个实根,该实根存在的充要条件是 (a) ≤0
即a2-ay + b2≤0,
y≥ 且x=a 时,等式成立,
故 .
∵ ,x=a 时等号成立,
而 在 上是减函数, x=a 时,
其值最小,
故x=a 时, y 有最小值, .
【解法4】
【解法5】
由0<x≤a<b 得
且b-x≥b-a>0
∴
∴
当x=a 时, .
【解法6】
令 = tan ,
∵ 0<x≤a<b , ∴
∴ .
且 时, .
即
