1.2《函数的概念和性质》课件(湘教版必修1)
文档属性
| 名称 | 1.2《函数的概念和性质》课件(湘教版必修1) |

|
|
| 格式 | zip | ||
| 文件大小 | 905.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-07-19 00:00:00 | ||
图片预览











文档简介
(共43张PPT)
1.2《函数的概念和性质》精品课件(湘教版必修1)
函数的概念与性质
1、函数的连续性
2、函数的间断点
3、 闭区间上连续函数的性质
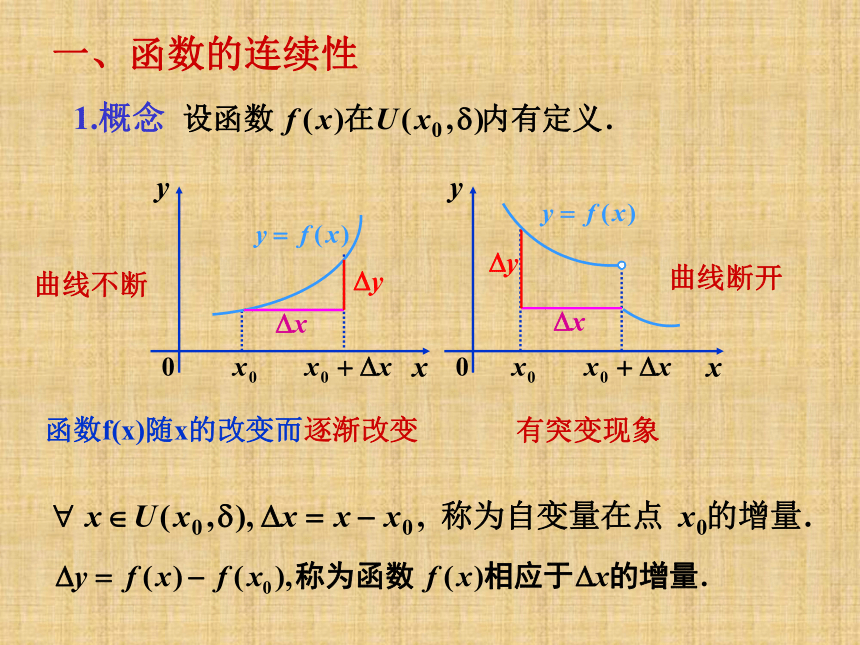
1.概念
一、函数的连续性
曲线不断
曲线断开
函数f(x)随x的改变而逐渐改变
有突变现象
2.连续的定义 P50
注:1) 函数 f(x) 在 x0 连续的等价写法(满足定义1的条件):
2) 若 y = f (x) 在 x0 处不连续,则称 y = f(x)在 x0 处间断。
3) 极限与连续的关系: 极限 连续
连续函数必有极限, 有极限不一定是连续函数. 例如
例1
证
3.单侧连续
定理
例2
解
右连续但不左连续 ,
4.连续函数与连续区间
在区间上每一点都连续的函数,叫做在该区间上的连续函数,或者说函数在该区间上连续.
连续函数的图形是一条连续而不间断的曲线.
例如, 基本初等函数在其定义域上连续,初等函数在其定义区间上连续.
例3
证
例4. 设
在x=0处连续,求常数a与b应满足的关系。
二、函数的间断点
1.跳跃间断点
例4
解
2.可去间断点
例5
解
如例5中,
跳跃间断点与可去间断点统称为第一类间断点.
特点
注意 可去间断点只要改变或者补充间断处函数的定义, 则可使其变为连续点.
3.第二类间断点
例6
解
例7
解
注意 不要以为函数的间断点只是个别的几个点.
狄利克雷函数
在定义域R内每一点处都间断,且都是第二类间断点.
★
★
仅在x=0处连续, 在定义域 R内其余各点处处间断. 但其绝对值处处连续.
例8 研究下列函数在x=0的连续性,若是间断的,指出间断点类型。
(a为任意实数)
解:1)
x=0为第一类间断点。
不存在,∴x=0为第二类间断点。
4)
∴当a=0时f4(x)在x=0处连续。
a≠0时 x=0为f(x)的可去间断点。
2)
3)
小结
1.函数在一点连续必须满足的三个条件;
3.间断点的分类与判别;
2.区间上的连续函数;
第一类间断点:可去型,跳跃型.
第二类间断点:无穷型,振荡型.
间断点
(见下图)
可去型
第一类间断点
o
y
x
跳跃型
无穷型
振荡型
第二类间断点
o
y
x
o
y
x
o
y
x
思考题
思考题解答
且
1、一类;一类;二类。
2、
但反之不成立.
例
但
§1.3.3 闭区间上连续函数的性质
最大值和最小值定理
介值定理
一、最大值和最小值定理
定义:
例如,
定理1(最大值和最小值定理) 在闭区间上连续的函数一定有最大值和最小值.
注意:1.若区间是开区间, 定理不一定成立;
2.若区间内有间断点, 定理不一定成立.
推论(有界性定理) 在闭区间上连续的函数一定在该区间上有界.
证
证:
∴取
当|x|>X时, | f (x)-A|<1
又||f (x)|-|A||<| f (x)-A|<1,
即: | f (x)|<|A|+1
∵ f(x) 在(-∞,+∞)上连续,∴ f(x)在[-X,X]上连续。
由最值定理, M0>0, x X, 都有| f (x)|取M=max{|A|+1, M0},
例1 设 f (x) 在(-∞, +∞)上连续,且 存在,
证明 f (x) 在(-∞, +∞)上有界。
有渐近线
二、介值定理
定义:
几何解释:
几何解释:
M
B
C
A
m
a
b
证
由零点定理,
推论 在闭区间上连续的函数必取得介于最大值 与最小值 之间的任何值.
例1
证
由零点定理,
例2
证
由零点定理,
例5 设f(x)在(a, b)内连续,x1,x2,……xn是(a, b)内任意值,
证明存在一点ξ∈(a, b)使
证:设
∵f(x)在(a, b)内连续, ∴f(x)在[x i , x j ]上连续。
x1,x2……xn∈[xi , xj]
由最值定理: f(x)在[xi ,xj ]上达到最大M=f(ξ1),
最小值m=f(ξ2),
即
据介值定理推论: 至少存在
使
小结
四个定理
最值定理;有界性定理;零点定理;介值定理.
注意 1.闭区间; 2.连续函数.
这两点不满足, 上述定理不一定成立.
解题思路
1.直接法:先利用最值定理,再利用介值定理;
2.辅助函数法:先作辅助函数F(x),再利用零点定理;
思考题
下述命题是否正确?
思考题解答
不正确.
例函数
1.2《函数的概念和性质》精品课件(湘教版必修1)
函数的概念与性质
1、函数的连续性
2、函数的间断点
3、 闭区间上连续函数的性质
1.概念
一、函数的连续性
曲线不断
曲线断开
函数f(x)随x的改变而逐渐改变
有突变现象
2.连续的定义 P50
注:1) 函数 f(x) 在 x0 连续的等价写法(满足定义1的条件):
2) 若 y = f (x) 在 x0 处不连续,则称 y = f(x)在 x0 处间断。
3) 极限与连续的关系: 极限 连续
连续函数必有极限, 有极限不一定是连续函数. 例如
例1
证
3.单侧连续
定理
例2
解
右连续但不左连续 ,
4.连续函数与连续区间
在区间上每一点都连续的函数,叫做在该区间上的连续函数,或者说函数在该区间上连续.
连续函数的图形是一条连续而不间断的曲线.
例如, 基本初等函数在其定义域上连续,初等函数在其定义区间上连续.
例3
证
例4. 设
在x=0处连续,求常数a与b应满足的关系。
二、函数的间断点
1.跳跃间断点
例4
解
2.可去间断点
例5
解
如例5中,
跳跃间断点与可去间断点统称为第一类间断点.
特点
注意 可去间断点只要改变或者补充间断处函数的定义, 则可使其变为连续点.
3.第二类间断点
例6
解
例7
解
注意 不要以为函数的间断点只是个别的几个点.
狄利克雷函数
在定义域R内每一点处都间断,且都是第二类间断点.
★
★
仅在x=0处连续, 在定义域 R内其余各点处处间断. 但其绝对值处处连续.
例8 研究下列函数在x=0的连续性,若是间断的,指出间断点类型。
(a为任意实数)
解:1)
x=0为第一类间断点。
不存在,∴x=0为第二类间断点。
4)
∴当a=0时f4(x)在x=0处连续。
a≠0时 x=0为f(x)的可去间断点。
2)
3)
小结
1.函数在一点连续必须满足的三个条件;
3.间断点的分类与判别;
2.区间上的连续函数;
第一类间断点:可去型,跳跃型.
第二类间断点:无穷型,振荡型.
间断点
(见下图)
可去型
第一类间断点
o
y
x
跳跃型
无穷型
振荡型
第二类间断点
o
y
x
o
y
x
o
y
x
思考题
思考题解答
且
1、一类;一类;二类。
2、
但反之不成立.
例
但
§1.3.3 闭区间上连续函数的性质
最大值和最小值定理
介值定理
一、最大值和最小值定理
定义:
例如,
定理1(最大值和最小值定理) 在闭区间上连续的函数一定有最大值和最小值.
注意:1.若区间是开区间, 定理不一定成立;
2.若区间内有间断点, 定理不一定成立.
推论(有界性定理) 在闭区间上连续的函数一定在该区间上有界.
证
证:
∴取
当|x|>X时, | f (x)-A|<1
又||f (x)|-|A||<| f (x)-A|<1,
即: | f (x)|<|A|+1
∵ f(x) 在(-∞,+∞)上连续,∴ f(x)在[-X,X]上连续。
由最值定理, M0>0, x X, 都有| f (x)|
例1 设 f (x) 在(-∞, +∞)上连续,且 存在,
证明 f (x) 在(-∞, +∞)上有界。
有渐近线
二、介值定理
定义:
几何解释:
几何解释:
M
B
C
A
m
a
b
证
由零点定理,
推论 在闭区间上连续的函数必取得介于最大值 与最小值 之间的任何值.
例1
证
由零点定理,
例2
证
由零点定理,
例5 设f(x)在(a, b)内连续,x1,x2,……xn是(a, b)内任意值,
证明存在一点ξ∈(a, b)使
证:设
∵f(x)在(a, b)内连续, ∴f(x)在[x i , x j ]上连续。
x1,x2……xn∈[xi , xj]
由最值定理: f(x)在[xi ,xj ]上达到最大M=f(ξ1),
最小值m=f(ξ2),
即
据介值定理推论: 至少存在
使
小结
四个定理
最值定理;有界性定理;零点定理;介值定理.
注意 1.闭区间; 2.连续函数.
这两点不满足, 上述定理不一定成立.
解题思路
1.直接法:先利用最值定理,再利用介值定理;
2.辅助函数法:先作辅助函数F(x),再利用零点定理;
思考题
下述命题是否正确?
思考题解答
不正确.
例函数
