2.1《指数与指数函数》课件(湘教版必修1)
文档属性
| 名称 | 2.1《指数与指数函数》课件(湘教版必修1) |

|
|
| 格式 | zip | ||
| 文件大小 | 98.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-07-19 00:00:00 | ||
图片预览





文档简介
(共12张PPT)
一、整数指数幂的运算性质
二、根式的概念
如果一个数的 n 次方等于 a(n>1 且 n∈N*), 那么这个数叫
做 a 的 n 次方根. 即: 若 xn=a, 则 x 叫做 a 的 n 次方根, 其中 n>1
且 n∈N*.
式子 a 叫做根式, 这里 n 叫做根指数, a 叫做被开方数.
n
(1)am·an=am+n (m, n∈Z);
(2)am÷an=am-n (a 0, m, n∈Z);
(3)(am)n=amn (m, n∈Z);
(4)(ab)n=anbn (n∈Z).
三、根式的性质
5.负数没有偶次方根.
6.零的任何次方根都是零.
1.当 n 为奇数时, 正数的 n 次方根是一个正数, 负数的 n 次方根是一个负数, a 的 n 次方根用符号 a 表示.
n
2.当 n 为偶数时, 正数的 n 次方根有两个, 它们互为相反数, 这时, 正数的正的 n 次方根用符号 a 表示, 负的 n 次方根用符号 - a 表示. 正负两个 n 次方根可以合写为 a (a>0).
n
n
n
3.( a )n=a.
n
4.当 n 为奇数时, an =a;
n
当 n 为偶数时, an =|a|=
n
a (a≥0),
-a (a<0).
五、有理数指数幂的运算性质
四、分数指数幂的意义
注: 0 的正分数指数幂等于 0, 0 的负分数指数幂没有意义.
函数 y=ax(a>0, 且a 1)叫做指数函数, 其中 x 是自变量, 函数的定义域是 R.
六、指数函数
a = am , a- = (a>0, m, n∈N*, 且 n>1).
n
m
n
n
m
n
m
a
1
(1)ar·as=ar+s (a>0, r, s∈Q);
(2)ar÷as=ar-s (a>0, r, s∈Q);
(3)(ar)s=ars (a>0, r, s∈Q);
(4)(ab)r=arbr (a>0, b>0, r∈Q).
图
象
性
质
y
o
x
(0, 1)
y=1
y=ax
(a>1)
a>1
y
o
x
(0, 1)
y=1
y=ax
(00(1) 定义域: R
(2) 值 域: (0, +∞)
(3) 过点(0, 1), 即 x=0 时, y=1.
(4) 在 R 上是增函数.
(4) 在 R 上是减函数.
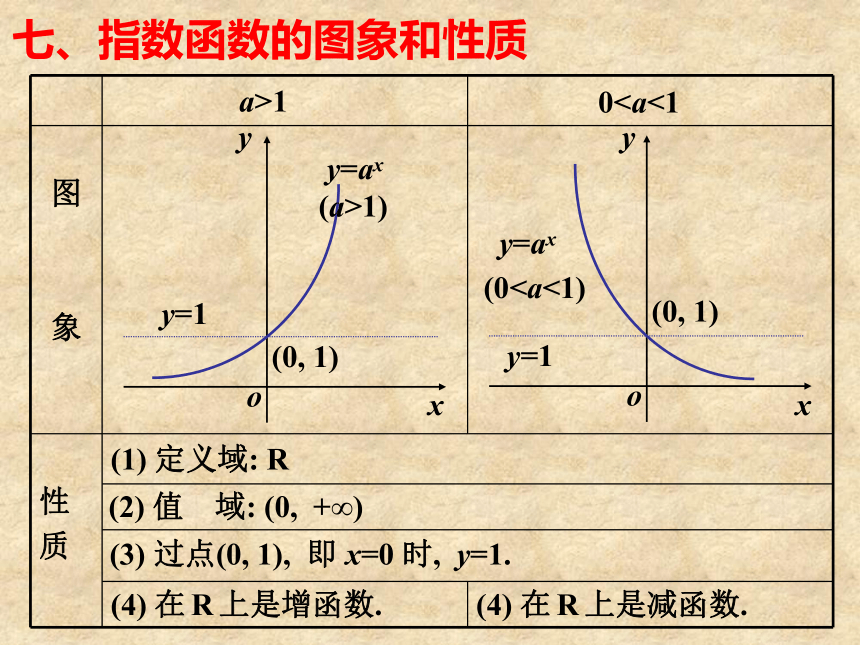
七、指数函数的图象和性质
课堂练习
1.若函数y=ax+b-1 (a>0, a 1) 图象经过第二、三、四象限, 则一定有( )
A. 00 B. a>1, b>0 C. 01, b<0
2.若 0A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.设 a=40.9, b=80.48, c=( )-1.5, 则( )
A. c>a>b B. b>a>c C. a>b>c D. a>c>b
1
2
4.若 0(1-a) >(1-a)b B. (1+a)a>(1+b)b
C. (1-a)b>(1-a) D. (1-a)a>(1-b)b
b
1
2
b
C
A
D
D
C
5.设 a=60.7, b=0.76, c=log0.76, 则( )
A. c>a>b B. b>a>c C. a>b>c D. a>c>b
典型例题
1.化简下列各式:
(1) (1-a) ;
(a-1)3
1
4
(2) xy2· xy-1 · xy ;
3
4
=- a-1 .
=xy.
解: (1)原式=(1-a)(a-1)-
4
3
=-(a-1)(a-1)-
4
3
=-(a-1)
4
1
(2)原式=[xy2(xy-1) ] (xy)
2
1
3
1
2
1
=(xy2x y- ) x y
3
1
2
1
2
1
2
1
2
1
=(x y ) x y
2
3
2
3
3
1
2
1
2
1
=x y x y
2
1
2
1
2
1
2
1
(3) (1-a)[(a-1)-2(-a) ] .
2
1
2
1
∴a-1<0.
(3)由(-a) 知 -a≥0,
2
1
∴原式=(1-a)(1-a)-1(-a)
4
1
=(-a) .
4
1
2.已知 2x+2-x=5, 求下列各式的值: (1) 4x+4-x; (2) 8x+8-x.
解: (1) 4x+4-x=(2x+2-x)2-2 2x · 2-x
(2) 8x+8-x=(2x+2-x)3-3 2x · 2-x(2x+2-x)
=25-2=23;
=125-15=110.
3.已知 2a · 5b=2c · 5d=10, 求证: (a-1)(d-1)=(b-1)(c-1).
证: 由已知 2a · 5b=10=2 · 5, 2c · 5d=10=2 · 5,
∴ 2a-1 · 5b-1=1, 2c-1 · 5d-1=1.
∴ 2(a-1)(d-1) · 5(b-1)(d-1) =1, 2(c-1)(b-1) · 5(d-1)(b-1) =1.
∴ 2(a-1)(d-1)=2(c-1)(b-1).
∴ (a-1)(d-1)=(b-1)(c-1).
∴ 2(a-1)(d-1) · 5(b-1)(d-1) =2(c-1)(b-1) · 5(d-1)(b-1).
4.若关于 x 的方程 2a2x-2-7ax-1+3=0 有一个根是 x=2, 求 a 的值并求方程其余的根.
a= 时, 方程的另一根为 x=1-log23; a=3时, x=1-log32 .
1
2
5.已知 2x= a + (a>1), 求 的值.
a
1
x- x2-1
x2-1
解: 以 x+ x2-1、 x- x2-1 为根构造方程:
t2-2xt+1=0,
即: t2-( a + )t+ a · =0,
a
1
a
1
a
1
∴t= a 或 .
∵ x+ x2-1 >x- x2-1 , a>1,
x- x2-1 = .
∴ x+ x2-1 = a ,
a
1
∴ x2-1 = ( a - ),
1
2
a
1
∴原式=
( a - )
1
2
a
1
a
1
= (a-1).
1
2
解法二: 将已知式整理得:
( a )2-2x a +1=0
或 ( )2-2x( )+1=0.
a
1
a
1
∵ a > ,
a
1
∴ a =x+ x2-1 , =x- x2-1 ,
a
1
以下同上.
6.已知函数 f(x)=3x 且 f-1(18)=a+2, g(x)=3ax-4x 的定义域为 [0, 1]. (1)求 g(x) 的解析式; (2)求 g(x) 的单调区间, 确定其增减性并用定义证明; (3)求 g(x) 的值域.
∴f(a+2)=3a+2=18.
解: (1)∵f(x)=3x 且 f-1(18)=a+2,
∴3a=2.
∴g(x)=(3a)x-4x=2x-4x.
即 g(x)=2x-4x.
(2)令 t=2x, 则函数 g(x) 由 y=t-t2 及 t=2x 复合而得.
由已知 x [0, 1], 则 t [1, 2],
∵t=2x 在 [0, 1] 上单调递增, y=t-t2 在 [1, 2] 上单调递减,
g(x) 在 [0, 1] 上单调递减, 证明如下:
∴g(x) 的定义域区间 [0, 1] 为函数的单调递减区间.
对于任意的 x1, x2 [0, 1], 且 x1g(x1)-g(x2)
∵0≤x1∴2x1-2x2<0 且 1-2x1-2x2<0.
∴ g(x1)-g(x2)
∴ g(x1)>g(x2).
故函数 g(x) 在 [0, 1] 上单调递减.
=(2x1-4x1)-(2x2-4x2)
=(2x1-2x2)-(2x1-2x2)(2x1+2x2)
=(2x1-2x2)(1-2x1-2x2)
=(2x1-2x2)(1-2x1-2x2)>0.
∴ x [0, 1] 时有:
解: (3)∵g(x) 在 [0, 1] 上单调递减,
g(1)≤g(x)≤g(0).
∵g(1)=21-41=-2, g(0)=20-40=0,
∴ -2≤g(x)≤0 .
故函数 g(x) 的值域为 [-2, 0].
6.已知函数 f(x)=3x 且 f-1(18)=a+2, g(x)=3ax-4x 的定义域为 [0, 1]. (1)求 g(x) 的解析式; (2)求 g(x) 的单调区间, 确定其增减性并用定义证明; (3)求 g(x) 的值域.
7.设 a>0, f(x)= - 是 R 上的奇函数. (1)求 a 的值; (2)试判断 f(x) 的反函数 f-1(x) 的奇偶性与单调性.
a
ex
a
ex
解: (1)∵ f(x) 是 R 上的奇函数,
∴f(0)=0,
即 -a=0.
1
a
∴a2=1.
∵a>0,
∴a=1.
(2)由 (1) 知 f(x)=ex-e-x, x R, f(x) R.
∵ f(x) 是奇函数,
∴ f(x) 的反函数 f-1(x) 也是奇函数.
∵ y=e-x 是 R 上的减函数,
∴ y=-e-x 是 R 上的增函数.
又∵ y=ex 是 R 上的增函数,
∴ y=ex -e-x 是 R 上的增函数.
∴ f(x) 的反函数 f-1(x) 也是 R 上的增函数.
综上所述, f-1(x) 是奇函数, 且是 R 上的增函数.
此时, f(x)=ex-e-x是 R 上的奇函数.
∴a=1 即为所求.
一、整数指数幂的运算性质
二、根式的概念
如果一个数的 n 次方等于 a(n>1 且 n∈N*), 那么这个数叫
做 a 的 n 次方根. 即: 若 xn=a, 则 x 叫做 a 的 n 次方根, 其中 n>1
且 n∈N*.
式子 a 叫做根式, 这里 n 叫做根指数, a 叫做被开方数.
n
(1)am·an=am+n (m, n∈Z);
(2)am÷an=am-n (a 0, m, n∈Z);
(3)(am)n=amn (m, n∈Z);
(4)(ab)n=anbn (n∈Z).
三、根式的性质
5.负数没有偶次方根.
6.零的任何次方根都是零.
1.当 n 为奇数时, 正数的 n 次方根是一个正数, 负数的 n 次方根是一个负数, a 的 n 次方根用符号 a 表示.
n
2.当 n 为偶数时, 正数的 n 次方根有两个, 它们互为相反数, 这时, 正数的正的 n 次方根用符号 a 表示, 负的 n 次方根用符号 - a 表示. 正负两个 n 次方根可以合写为 a (a>0).
n
n
n
3.( a )n=a.
n
4.当 n 为奇数时, an =a;
n
当 n 为偶数时, an =|a|=
n
a (a≥0),
-a (a<0).
五、有理数指数幂的运算性质
四、分数指数幂的意义
注: 0 的正分数指数幂等于 0, 0 的负分数指数幂没有意义.
函数 y=ax(a>0, 且a 1)叫做指数函数, 其中 x 是自变量, 函数的定义域是 R.
六、指数函数
a = am , a- = (a>0, m, n∈N*, 且 n>1).
n
m
n
n
m
n
m
a
1
(1)ar·as=ar+s (a>0, r, s∈Q);
(2)ar÷as=ar-s (a>0, r, s∈Q);
(3)(ar)s=ars (a>0, r, s∈Q);
(4)(ab)r=arbr (a>0, b>0, r∈Q).
图
象
性
质
y
o
x
(0, 1)
y=1
y=ax
(a>1)
a>1
y
o
x
(0, 1)
y=1
y=ax
(0
(2) 值 域: (0, +∞)
(3) 过点(0, 1), 即 x=0 时, y=1.
(4) 在 R 上是增函数.
(4) 在 R 上是减函数.
七、指数函数的图象和性质
课堂练习
1.若函数y=ax+b-1 (a>0, a 1) 图象经过第二、三、四象限, 则一定有( )
A. 0
2.若 0
3.设 a=40.9, b=80.48, c=( )-1.5, 则( )
A. c>a>b B. b>a>c C. a>b>c D. a>c>b
1
2
4.若 0
C. (1-a)b>(1-a) D. (1-a)a>(1-b)b
b
1
2
b
C
A
D
D
C
5.设 a=60.7, b=0.76, c=log0.76, 则( )
A. c>a>b B. b>a>c C. a>b>c D. a>c>b
典型例题
1.化简下列各式:
(1) (1-a) ;
(a-1)3
1
4
(2) xy2· xy-1 · xy ;
3
4
=- a-1 .
=xy.
解: (1)原式=(1-a)(a-1)-
4
3
=-(a-1)(a-1)-
4
3
=-(a-1)
4
1
(2)原式=[xy2(xy-1) ] (xy)
2
1
3
1
2
1
=(xy2x y- ) x y
3
1
2
1
2
1
2
1
2
1
=(x y ) x y
2
3
2
3
3
1
2
1
2
1
=x y x y
2
1
2
1
2
1
2
1
(3) (1-a)[(a-1)-2(-a) ] .
2
1
2
1
∴a-1<0.
(3)由(-a) 知 -a≥0,
2
1
∴原式=(1-a)(1-a)-1(-a)
4
1
=(-a) .
4
1
2.已知 2x+2-x=5, 求下列各式的值: (1) 4x+4-x; (2) 8x+8-x.
解: (1) 4x+4-x=(2x+2-x)2-2 2x · 2-x
(2) 8x+8-x=(2x+2-x)3-3 2x · 2-x(2x+2-x)
=25-2=23;
=125-15=110.
3.已知 2a · 5b=2c · 5d=10, 求证: (a-1)(d-1)=(b-1)(c-1).
证: 由已知 2a · 5b=10=2 · 5, 2c · 5d=10=2 · 5,
∴ 2a-1 · 5b-1=1, 2c-1 · 5d-1=1.
∴ 2(a-1)(d-1) · 5(b-1)(d-1) =1, 2(c-1)(b-1) · 5(d-1)(b-1) =1.
∴ 2(a-1)(d-1)=2(c-1)(b-1).
∴ (a-1)(d-1)=(b-1)(c-1).
∴ 2(a-1)(d-1) · 5(b-1)(d-1) =2(c-1)(b-1) · 5(d-1)(b-1).
4.若关于 x 的方程 2a2x-2-7ax-1+3=0 有一个根是 x=2, 求 a 的值并求方程其余的根.
a= 时, 方程的另一根为 x=1-log23; a=3时, x=1-log32 .
1
2
5.已知 2x= a + (a>1), 求 的值.
a
1
x- x2-1
x2-1
解: 以 x+ x2-1、 x- x2-1 为根构造方程:
t2-2xt+1=0,
即: t2-( a + )t+ a · =0,
a
1
a
1
a
1
∴t= a 或 .
∵ x+ x2-1 >x- x2-1 , a>1,
x- x2-1 = .
∴ x+ x2-1 = a ,
a
1
∴ x2-1 = ( a - ),
1
2
a
1
∴原式=
( a - )
1
2
a
1
a
1
= (a-1).
1
2
解法二: 将已知式整理得:
( a )2-2x a +1=0
或 ( )2-2x( )+1=0.
a
1
a
1
∵ a > ,
a
1
∴ a =x+ x2-1 , =x- x2-1 ,
a
1
以下同上.
6.已知函数 f(x)=3x 且 f-1(18)=a+2, g(x)=3ax-4x 的定义域为 [0, 1]. (1)求 g(x) 的解析式; (2)求 g(x) 的单调区间, 确定其增减性并用定义证明; (3)求 g(x) 的值域.
∴f(a+2)=3a+2=18.
解: (1)∵f(x)=3x 且 f-1(18)=a+2,
∴3a=2.
∴g(x)=(3a)x-4x=2x-4x.
即 g(x)=2x-4x.
(2)令 t=2x, 则函数 g(x) 由 y=t-t2 及 t=2x 复合而得.
由已知 x [0, 1], 则 t [1, 2],
∵t=2x 在 [0, 1] 上单调递增, y=t-t2 在 [1, 2] 上单调递减,
g(x) 在 [0, 1] 上单调递减, 证明如下:
∴g(x) 的定义域区间 [0, 1] 为函数的单调递减区间.
对于任意的 x1, x2 [0, 1], 且 x1
∵0≤x1
∴ g(x1)-g(x2)
∴ g(x1)>g(x2).
故函数 g(x) 在 [0, 1] 上单调递减.
=(2x1-4x1)-(2x2-4x2)
=(2x1-2x2)-(2x1-2x2)(2x1+2x2)
=(2x1-2x2)(1-2x1-2x2)
=(2x1-2x2)(1-2x1-2x2)>0.
∴ x [0, 1] 时有:
解: (3)∵g(x) 在 [0, 1] 上单调递减,
g(1)≤g(x)≤g(0).
∵g(1)=21-41=-2, g(0)=20-40=0,
∴ -2≤g(x)≤0 .
故函数 g(x) 的值域为 [-2, 0].
6.已知函数 f(x)=3x 且 f-1(18)=a+2, g(x)=3ax-4x 的定义域为 [0, 1]. (1)求 g(x) 的解析式; (2)求 g(x) 的单调区间, 确定其增减性并用定义证明; (3)求 g(x) 的值域.
7.设 a>0, f(x)= - 是 R 上的奇函数. (1)求 a 的值; (2)试判断 f(x) 的反函数 f-1(x) 的奇偶性与单调性.
a
ex
a
ex
解: (1)∵ f(x) 是 R 上的奇函数,
∴f(0)=0,
即 -a=0.
1
a
∴a2=1.
∵a>0,
∴a=1.
(2)由 (1) 知 f(x)=ex-e-x, x R, f(x) R.
∵ f(x) 是奇函数,
∴ f(x) 的反函数 f-1(x) 也是奇函数.
∵ y=e-x 是 R 上的减函数,
∴ y=-e-x 是 R 上的增函数.
又∵ y=ex 是 R 上的增函数,
∴ y=ex -e-x 是 R 上的增函数.
∴ f(x) 的反函数 f-1(x) 也是 R 上的增函数.
综上所述, f-1(x) 是奇函数, 且是 R 上的增函数.
此时, f(x)=ex-e-x是 R 上的奇函数.
∴a=1 即为所求.
