【专项练习】函数图像问题的类型与解法 (含答案)
文档属性
| 名称 | 【专项练习】函数图像问题的类型与解法 (含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-29 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
函数图像问题的类型与解法
理解函数图像的定义,掌握函数图像的基本作法是学习函数知识的基础之一,运用函数图像解答函数问题又是不可或缺的基本技能。函数图像主要包括:①函数图像的基本作法;②函数图像的识别;③函数图像的运用。纵观近几年数学的各种考试,函数图像问题主要有:①已知函数解析式,求作函数图像;②已知函数图像,确定函数解析式;③运用函数图像解答数学问题等几种类型。各种类型问题结构上具有相应的特征,解答方法也有一定的规律可寻。那么在实际解答函数图像问题时,到底应该如何抓住问题的结构特征,快捷,准确地给予解答呢?下面通过典型例题的详细解析来回答这个问题。
【典例1】解答下列问题:
y
1、已知y=f(x)的图像如右图所示,那么函数
Y=f(2-x)的图像是(
)
-2
-1
0
1
2
x
Y
y
y
y
-1
0
1
2
x
-2
-1
0
1
x
-1
0
1
2
x
-2
-1
0
1
x
A
B
C
D
【解析】
【知识点】①函数图像及运用;②函数图像平移变换的基本方法;③函数图像对称变换的基本方法。
【解题思路】根据函数图像的性质和函数图像平移变换,对称变换的基本方法,可知函数Y=f(2-x)的图像是将函数y=f(x)的图像沿Y轴对称变换,再向右平移2个单位长度后得到的图像,从而就可得出选项。
【详细解答】函数Y=f(2-x)的图像是将函数y=f(x)的图像沿Y轴对称变换,再向右平移2个单位长度后得到的图像,选项C的图像符合,C正确,选C。
2、下列函数的图像中,经过平移或翻折后不能与函数f(x)=x的图像重合的函数是(
)
A
f(x)=
B
f(x)=
x
C
f(x)=
D
f(x)=
+1
【解析】
【知识点】①函数图像及运用;②函数图像平移变换的基本方法;③函数图像翻折变换的基本方法;④指数函数的定义与性质;⑤对数函数的定义与性质。
【解题思路】根据指数函数和对数函数的性质,运用函数图像平移变换和翻折变换的基本方法,对各选项函数的图像通过平移变换或翻折变换能否得到函数f(x)=x的图像进行判断就可得出选项。
【详细解答】对A,函数f(x)=
的图像与函数f(x)=x的图像关于直线y=x对称,只需把函数f(x)=
的图像沿直线y=x翻折就可得到函数f(x)=x的图像,即A错误;对B,函数f(x)=
x的图像与函数f(x)=x的图像关于X轴对称,只需把函数f(x)=
x的图像沿X轴翻折就可得到函数f(x)=x的图像,即B错误;对C,函数f(x)=
=,无论通过怎样的平移变换或翻折变换都不能得到函数f(x)=x的图像,C正确,选C。
3、为了得到函数f(x)=lg的图像,只需把函数f(x)=lgx的图像上所有的点(
)
A
向左平移3个单位长度,再向上平移1个单位长度
B
向右平移3个单位长度,再向上平移1个单位长度
C
向左平移3个单位长度,再向下平移1个单位长度
D
向右平移3个单位长度,再向下平移1个单位长度
【解析】
【知识点】①函数图像及运用;②函数图像平移变换的基本方法;③对数的定义与性质;④对数运算性质及运用。
【解题思路】根据对数的性质和对数的运算性质,得到f(x+3)-1=lg(x+3)-lg10=
lg,运用函数图像的性质和函数图像平移变换的基本方法,可知函数函数f(x)=lgx的图像上所有的点向左平移3个单位长度,再向下平移一个单位长度能够得到函数f(x)=lg的图像,从而就可得出选项。
【详细解答】函数f(x+3)-1=
lg(x+3)-lg10=
lg,函数函数f(x)=lgx的图像上所有的点向左平移3个单位长度,再向下平移一个单位长度能够得到函数f(x)=lg的图像,
C正确,选C。
y
4、设奇函数f(x)的定义域是[-5,5],若当
x[0,5]时,f(x)的图像如图所示,则不
等式f(x)<0的解集是
;
-2
-1
0
2
5
x
【解析】
【知识点】①函数图像及运用;②奇函数的定义与性质;③求解不等式的基本方法。
【解题思路】根据奇函数的性质和函数图像,作出函数f(x)
x[-5,0]时的图像,运用函数图像和求解不等式的基本方法,结合问题条件得到关于x的不等式,求解不等式就可求出不等式f(x)<0的解集。
【详细解答】函数f(x)是奇函数,作出函数f(x)
x[-5,0]时的图像如图所示,
由图知,f(x)<0,-25,不等式f(x)<0的解集为(-2,0)(2,5]。
5、作出下列函数的图像:
(1)
y=|x-1|(x+1);
(2)y=
;
(3)
y=|(x+1)|;
(4)
y=;
(5)
y=
-2|x|-1;
(6)
y=3sin(2x-
)。
【解析】
【知识点】①函数图像的定义与性质;②作函数图像的基本方法。
【解题思路】根据函数图像的性质,运用作函数图像的基本方法就可作出各函数的图像。
【详细解答】(1)y=|x-1|(x+1)=
-1,x1,
(2)y==
,x0,
1-,x<1,
=,x<0,
函数y=|x-1|(x+1)的图像如图所示;
函数y=的图像如图所示;
(3)
y=|(x+1)|=
(x+1),x0,
(4)
y===2+
-(x+1),-1,
函数y=|(x+1)|的图像如图所示;
函数y=的图像如图所示;
(5)y=
-2|x|-1=-2x-1,x0,
(6)y=3sin(2x-
)=3sin[2(x-
)],
+2x-1,x<0,
函数y=
-2|x|-1的图像如图所示;
函数y=3sin(2x-
)的图像如图所示。
y
y
y
1
1
-1
0
1
x
-1
0
1
x
-1
0
1
x
-1
(1题图)
(2题图)
(3题图)
y
y
y
2
1
1
-1
0
1
x
-1
0
1
x
-1
0
1
x
-1
-1
(4题图)
(5题图)
(6题图)
『思考问题1』
(1)【典例1】是求作函数图像的问题,这类问题主要包括:①已知函数解析式,求作函数图像;②函数图像的平移变换;③函数图像的伸缩变换;④函数图像的对称变换;⑤函数图像的翻折变换;⑥函数图像的旋转变换;解答这类问题需要理解函数图像的定义,掌握函数图像的基本作法;函数图像的基本方法有:①直接作图法;②描点作图法;③图像变换法;
(2)面对问题应该选用哪种作图方法,需根据题给条件和所求问题来确定;
(3)应用图像变换法作图需要熟练掌握几种基本函数(一次函数,二次函数,反比例函数,指数函数,对数函数,幂函数,正弦函数,余弦函数)的图像,注意图像变换的顺序。
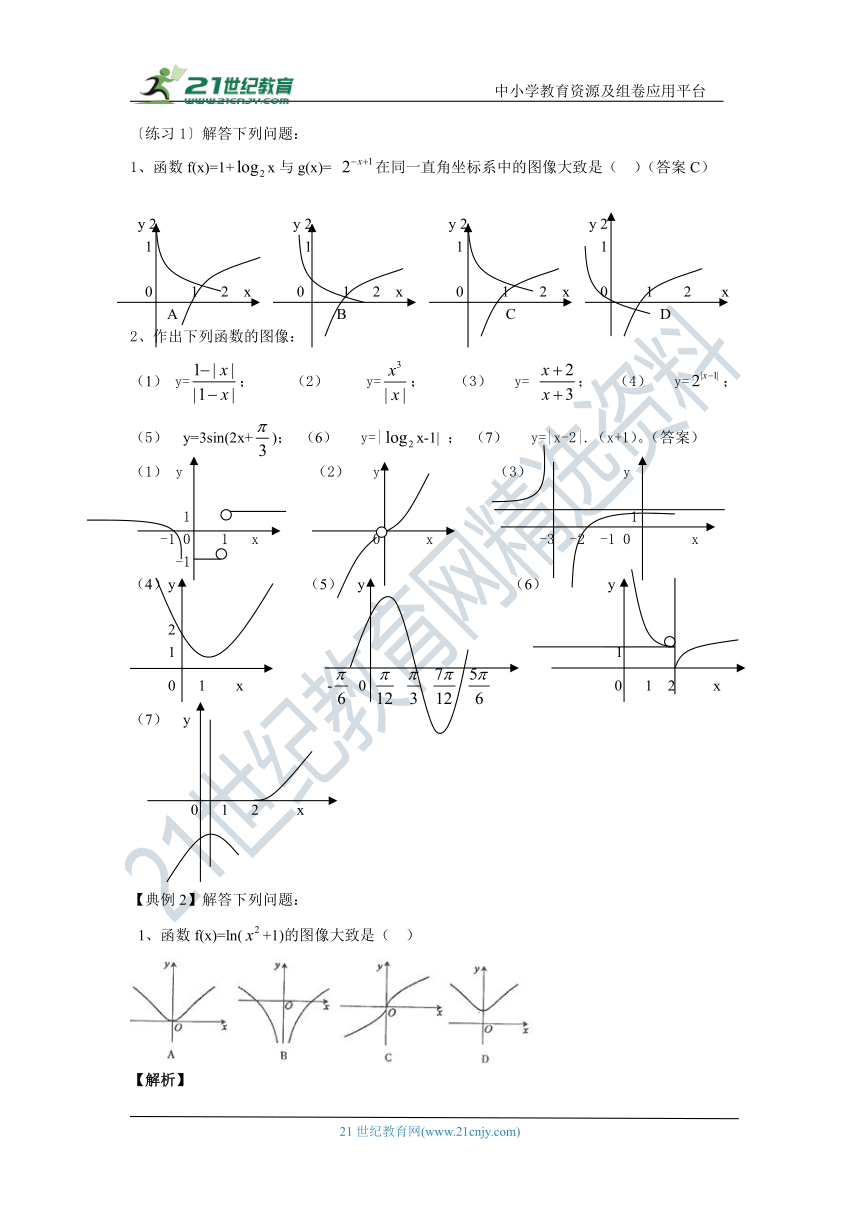
〔练习1〕解答下列问题:
1、函数f(x)=1+x与g(x)=
在同一直角坐标系中的图像大致是(
)(答案C)
y
2
y
2
y
2
y
2
1
1
1
1
0
1
2
x
0
1
2
x
0
1
2
x
0
1
2
x
A
B
C
D
2、作出下列函数的图像:
(1)
y=;
(2)
y=;
(3)
y=
;
(4)
y=;(5)
y=3sin(2x+);
(6)
y=|x-1|
;
(7)
y=|x-2|.(x+1)。(答案)
(1)
y
(2)
y
(3)
y
1
1
-1
0
1
x
0
x
-3
-2
-1
0
x
-1
(4)y
(5)
y
(6)
y
2
1
1
0
1
x
-
0
0
1
2
x
(7)
y
0
1
2
x
【典例2】解答下列问题:
1、函数f(x)=ln(+1)的图像大致是(
)
【解析】
【知识点】①对数函数的定义,图像与性质;②函数图像及运用;③作函数图像的基本方法。
【解题思路】根据对数函数的性质和图像,运用作函数图像的基本方法,由f(0)=ln(0+1)=0,可以排除B,D,由
f(-x)=
=ln[+1]=
=ln(+1)=
f(x),得到函数f(x)是偶函数,可以排除C,从而就可得出选项。
【详细解答】函数f(x)=ln(+1)的定义域为R,f(0)=ln(0+1)=0,可以排除B,D,ff(-x)=
=ln[+1]=
=ln(+1)=
f(x),函数f(x)是偶函数,可以排除C,A正确,选A。
y
2、右图中的图像所表示的函数的解析式为(
)
-----------|
A
y=|x-1|
(0≤x≤2)
B
y=-|x-1|(0≤x≤2)
|
C
y=-|x-1|
(0≤x≤2)
D
y=1-|x-1|
(0≤x≤2)
0
1
2
x
【解析】
【知识点】①函数图像及运用;②根据函数图像确定函数解析式的基本方法。
【解题思路】根据函数图像,
f(0)
=0,可以排除A,C,
f(1)=
,可以排除D,从而就可得出选项。
【详细解答】由函数f(x)的图像得:f(0)
=0,对A,f(0)=
|0-1|=,对C,f(0)=
-|0-1|=
-1=,排除A,C;
f(1)=
,对D,f(1)=1-|0-1|=1-1=0,排除D,B正确,选B。
3、已知函数y=f(x)的大致图像如图所示,则函数
y
y=f(x)的解析式可能为(
)
A
f(x)=
lnx
B
f(x)=
ln|x|
C
f(x)=
ln|x|
D
f(x)=
ln|x|
0
x
【解析】
【知识点】①函数图像及运用;②根据函数图像确定函数解析式的基本方法。
【解题思路】根据函数图像,可知函数f(x)的定义域为(-
,0)(0,+
),可排除A;由函数f(x)在(-
,0)上单调递减,在(0,+
)上单调递增,可排除B;函数y=f(x)不是偶函数,可以排除D,从而就可得出选项。
【详细解答】根据函数图像,可知函数f(x)的定义域为(-
,0)(0,+
),可排除A;函数f(x)在(-
,0)上单调递减,在(0,+
)上单调递增,可排除B;函数f(x)不是偶函数,
可以排除D,C正确,选C。
4、函数f(x)=
的图像大致为(
)
y
y
y
y
1
1
1
1
0
1
x
0
1
x
0
1
x
0
1
x
A
B
C
D
【解析】
【知识点】①函数图像及运用;②根据函数图像确定函数解析式的基本方法。
【解题思路】根据函数f(x)=
=1+=1+,可知函数f(x)的定义域为(-
,0)(0,+
),可排除C,D,由当x>0时,函数f(x)=
1+单调递减,可以排除B,从而就可得出选项。
【详细解答】函数f(x=
=1+=1+的定义域为(-
,0)(0,+
),排除C,D;当x>0时,函数f(x)=
1+单调递减,
排除B,A正确,选A。
5、如图已知,圆心在上,半径为1m的圆O在t=0时与相切于点A,圆O沿以1m/s的速度匀速向上移动,圆被直线所截上方圆弧长记为x,令y=cosx,则y与时间t(0≤t≤1,单位:s)的函数y=f(t)的图像大致为()
A
B
C
D
【解析】
【知识点】①函数图像及运用;②圆的定义与性质;③余弦三角函数的定义,性质与图像。
【解题思路】根据圆和余弦三角函数的性质,得到cos==1-t,从而得到y=cosx=2-1(0≤t≤1),确定出函数y=f(t)的图像就可得出选项。
【详细解答】如图,
cos==1-t,
y=f(t)
=
cosx=2-1,
f(0)=2-1=1,f(1)=0-1=-1,
B选项的图像符合题意,B正确,选B。
『思考问题2』
(1)
【典例2】是函数图像的识图与辨图问题,这类问题常见的类型有:①已知函数图像,确定函数解析式选;②已知函数解析式,确定函数的图像;
(2)已知函数图像,确定函数解析式的基本方法是:①从图像的左右,上下分布观察函数定义域域和函数的值域;②
从图像的变化趋势观察函数的单调性;③
从图像的对称性观察函数的奇偶性;④从图像的循环往复观察函数的周期性;
(3)已知函数的解析式,确定函数图像的基本方法是:①从函数的定义域判断图像的左右位置,从函数的值域判断图像上下位置;②从函数的单调性,判断图像的变化趋势;③从函数的奇偶性,判断图像的对称性;④从函数的周期性,判断图像的循环往复;⑤从函数的极值点判断函数的最值点。
〔练习2〕解答下列问题:
y
1、已知函数y=f(x)的图像如右图,求函数
Y=f(x)的解析式。(答案f(x)=|x|-1)
-1
0
1
x
2、若函数f(x)=sinax+b(x>0),的图像如图所示,则函数g(x)=
(x+b)的图像可能是(
)
y
y
y
y
y
1
1
1
1
1
0
2
3
x
0
1
2
3
x
0
1
2
3
x
0
1
2
3
x
0
1
2
3
x
-1
-1
A
-1
B
-1
C
-1
D(答案C)
3、已知函数y=f(x)和函数y=g(x)的图像如图(1),
y
y
(2)所示,则函数F(x)=f(x).g(x)的图像可能
是(
)(答案A)
0
x
0
x
y
y
y
(1)
y
(2)
0
x
0
x
0
x
0
x
A
B
C
D
4、已知lga+lgb=0,则函数f(x)=与函数g(x)=
(x+b)的图像可能是(
)(答案B)
y
y
y
y
1
1
1
1
0
1
x
0
1
x
0
1
x
0
1
x
A
B
C
D
5、已知函数f(x)=
,则y=f(x)的图像大致为(
)(答案C)
y
y
y
y
1
1
1
0
1
x
1
0
1
x
0
1
x
0
1
x
A
B
C
D
6、函数f(x)=-xcosx的部分图像是(
)(答案B)
y
y
y
y
0
x
0
x
0
x
0
x
A
B
C
D
【典例3】解答下列问题:
y
1、已知f(x)=a+b+cx+d的图像如图所示,则(
)
0
1
2
x
A
b
(-∞,0)
B
b
(0,1)
C
b
(1,2)
D
b
(2,+∞)
【解析】
【知识点】①函数图像及运用;②函数零点的定义与性质;③运用函数图像确定函数解析式中参数取值范围的基本方法。
【解题思路】根据函数图像和函数零点的性质,得到关于a,b,c,d
的方程组,求解方程组求出a,c,d关于参数b的表示式,从而得到函数f(x)只含参数b的解析式,运用函数图像确定参数b的取值范围就可得出选项。
【详细解答】f(0)=0+0+0+d=0①,f(1)=a+b+c+d=0②,f(2)=8a+4b+2c+d=0③,联立①②③解得:a=-,c=-,d=0,f(x)=-
+b-x=-x(-3x+2)=
-x(x-1)(x-2),
x>2时,f(x)>0恒成立,
->0,即b<0,A正确,选A。
2、若函数f(x)的反函数为(x),则函数f(x-1)与函数(x-1)的图像可能是(
)
2
y
2
y
2
y
2
y
1
1
1
1
0
1
2
x
0
1
2
x
0
1
2
x
0
1
2
x
A
B
C
D
【解析】
【知识点】①函数图像及运用;②函数反函数的定义与性质;③指数函数的定义与性质;④对数函数的定义与性质;⑤函数图像平移变换的基本方法。
【解题思路】根据函数反函数,指数函数和对数函数的性质,结合图像得到指数函数和对数函数的底数都大于1,运用函数图像平移变换的基本方法确定出符合题意的图像就可得出选项。
【详细解答】指数函数与对数函数互为反函数,由图知指数函数和对数函数的底数都大于1,函数f(x-1)与函数(x-1)的图像是由函数f(x)与函数(x)的图像向右平移一个单位长度而得到,可以排除A,C,D,B正确,选B。
3、已知函数y=f(x)的图像是下列四个图像之一,且其导函数y=(x)的图像如图所示,则该函数的图像是(
)
【解析】
【知识点】①函数图像及运用;②函数导函数的定义与性质;③运用函数导函数判断函数单调性的基本方法。
【解题思路】根据函数导函数的图像和运用函数导函数判断函数单调性的基本方法,得到函数y=f(x)在(-1,1)上单调递增,且在(-1,0)上增长速度越来越快,在(0,1)上增长速度越来越慢,可以排除A,C,D,从而就可得出选项。
【详细解答】由导函数y=(x)的图像可知,函数y=f(x)在(-1,1)上单调递增,且在(-1,0)上增长速度越来越快,在(0,1)上增长速度越来越慢,可以排除A,C,D,B正确,选B。
4、已知函数y=f(x)的周期为2,当x[-1,1]时,f(x)=
,那么函数y=f(x)的图像与函数y=|lgx|的图像的交点共有(
)
A
10个
B
9个
C
8个
D
1个
【解析】
【知识点】①函数图像及运用;②周期函数的定义与性质;③对数函数的定义与性质。
【解题思路】根据周期函数和对数函数的性质,运用作函数图像的基本方法,在同一直角坐标系中作出函数y=f(x)和函数y=|lgx|的图像,由图像确定两个函数图像的交点的个数就可得出选项。
lgx,x1,
y
【详细解答】
y=|lgx|=
-lgx,0)的周期为2,当x[-1,1]时,f(x)=
,在同
1
一直角坐标系中作出函数y=f(x)和函数y=|lgx|的图
-1
0
1
2
x
像如图所示,由图知函数y=f(x)的图像与函数y=|lgx|的图像的交点共有10个,A正确,选A。
5、已知函数y=
的图像与函数y=kx的图像恰有两个交点,则实数k的取值范围是
;
【解析】
【知识点】①函数图像及运用;②绝对值的定义与性质;③一元一次函数的定义与性质;④分段函数的定义与性质;⑤求函数解析式中参数取值范围的基本方法。
【解题思路】根据绝对值的性质,把函数y=
化为分段函数,运用分段函数,一元一次函数的性质和已知函数解析式作函数图像的基本方法,在同一直角坐标系中作出函数y=
,函数y=kx的图像,利用函数图像就可求出实数k的取值范围。
【详细解答】函数y=
=x+1,x<-1或x>1,
y
-x-1,-1≤x<1,在同一直角坐
标系中作出函数y=
,函数y=kx的图像如图所示,
-1
0
1
x
由图知,-1<-k<0,或-2<-k<-1,0<k<1或1<k<2,若函数y=
的图像与函数y=kx的图像恰有两个交点,则实数k的取值范围是(0,1)(1,2)。
6、如图,|OA|=2(单位:m),|OB|=1(单位:m),
D
OA与OB的夹角为,以A为圆心,AB为半径
B
作圆弧BDC与线段OA延长线交于点C,甲,乙
0
A
C
两质点同时从点O出发,甲先以速率1(单位:m/s)沿线段OB行至点B,再以速率3(单位:m/s)沿圆弧BDC行至点C后停止;乙以速率2(单位:m/s)沿线段OA行至点A后停止,设t时刻甲,乙所到达的两点连线与它们经过的路径所围成的面积为S(t)(S(0)=0),则函数y=S(t)的图像大致是(
)
y
y
y
y
0
x
0
x
0
x
0
x
A
B
C
D
【解析】
【知识点】①函数图像及运用;②求函数解析式的基本方法;③三角形面积公式及运用;④扇形面积公式及运用。
【解题思路】根据三角形面积公式,扇形面积公式和求函数解析式的基本方法,结合时间点1求出t时刻甲、乙所到达的两点连线与它们经过的路径所围成的面积S(t)的解析式,运用函数解析式确定出函数S(t)的图像就可得出选项。
【详细解答】①当0≤t≤1时,
S(t)=
t.2tsin=;②1<1≤(为甲质点到达点C所需的时间)时,S(t)=
+3|AB|(t-1)=+(t-1);③当t>时,S(t)为一个常数,可以排除C;函数S(t)在[0,1]上单调递增,且函数图像是向下凸的,可以排除B,D,A正确,选A。
7、若关于x的不等式>x+m的解为-≤x<4,求实数m的值。
【解析】
【知识点】①函数图像及运用;②幂函数的定义与性质;③求解不等式的基本方法;④求函数解析式中参数值的基本方法。
【解题思路】根据幂函数和一元一次函数的性质,运用已知函数解析式作函数图像的基本方法在同一直角坐标系中作出函数f(x)=
,函数g(x)=x+m的图像,运用函数图像就可求出实数m的值。
y
【详细解答】在同一直角坐标系中作出函数
1
f(x)=
,函数g(x)=x+m的图像如图
-0
4
x
所示,关于x的不等式>x+m的解为-≤x<4,由图知函数f(x)与函数g(x)的图像相交于点(4,3),f(4)==3=g(4)=4+m,
m=-1,若关于x的不等式>x+m的解为-≤x<4,则实数m的值为-1。
『思考问题3』
(1)【典例3】是函数图像的运用问题,这类问题主要包括:①运用函数图像研究函数的性质;②运用函数图像求解不等式;③运用函数图像求函数的零点;
(2)解答函数图像运用问题的常用方法是:①定性分析法;②定量分析法;③函数模型法。
〔练习3〕解答下列问题:
1、已知函数f(x)=
(a>0,且a≠0)在同一直角坐标系中(x)与y=的图像可能是(
)(答案C)
2
y
2
y
2
y
2
y
1
--|
1
---
|
1
---
|
1
---
|
|
|
|
|
-10
1
2
x
-1
0
1
2
x
-1
0
1
2
x
-1
0
1
2
x
A
B
C
D
2、如果函数f(x)=
+的图像沿x轴向右平移a个单位得到曲线C,设曲线C的方程为y=g(x),对任意xR,都有g(1+x)=-g(1-x),试求g(1)+g(-1)的值。(答案-8-)
3、a为何值时,方程lg(3-x)+lg(x-1)=lg(a-x)有两解,一解,无解?(答案当3时,原方程无解。)
【考题演练】
【典例4】解答下列问题:
1、函数f(x)=cosx.ln(-x)在[-1,1]的图像大致为(
)(2020成都市高三二诊)
【解析】
【知识点】①函数图像及运用;②函数奇偶性的定义与性质;③判断函数奇偶性的基本方法;④函数单调性的定义与性质;⑤判断函数单调性的基本方法。
【解题思路】根据函数奇偶性的性质和判断函数奇偶性的基本方法,得到函数f(x)是奇函数,运用函数单调性的性质和判断函数单调性的基本方法,得到函数f(x)
在[0,1]上单调递增,从而确定函数f(x)=cosx.ln(-x)在[-1,1]的图像大致就可得出选项。
【详细解答】
f(-x)=cos(-x).ln(+x)=
cosx
ln(+x)=
cosx
ln[(+x)
.
]=
cosx
ln()=cosx
ln()=-cosx.ln(-x)=-
f(x),函数f(x)是奇函数,排除C,D;当x[0,1]时,函数y=
cosx单调递减,函数y=ln
(-x)单调递增,函数f(x)
在[0,1]上单调递减,排除A,B正确,选B。
2、函数y=
在[-6,6]的大致图像为(
)(2019全国高考新课标III(理))
A
B
C
D
【解析】
【知识点】①函数图像及运用;②函数奇偶性的定义与性质;③判断函数奇偶性的基本方法;④求函数值的基本方法。
【解题思路】根据函数奇偶性的性质和判断函数奇偶性的基本方法,结合问题条件得到函数y=
是奇函数,排除C;运用求函数值的基本方法求出当x=6时的函数值y=7>0,排除A,D就可得出选项。
【详细解答】设f(x)=
,函数f(x)的定义域为R关于原点对称,f(-x)
=
=-=-
f(x),函数f(x)是奇函数,排除C;
f(6)=
=
=7,排除A,D,B正确,选B。
3、已知函数f(x)=
|lnx|,x>0,和g(x)=a(aR且为常数),有以下结论:①当a=4时,
-+mx,x0,存在实数m,使得关于x的方程f(x)=g(x)有四个不
同的实数根;②存在m[3,4],使得关于x的方程f(x)=g(x)有三个不同的实数根;③当
x>0时,若函数h(x)=
(x)+bf(x)+c恰有三个不同的零点,,,则=1;
④当m=-4时,关于x的方程f(x)=g(x)
有四个不同的实数根,,,,且<
<<,若f(x)在[,]上的最大值为ln4,则sin(3+3+5+4)=1,
其中正确结论的个数是(
)(2018—2019成都市高一上期调研考试)
A
1个
B
2个
C
3个
D
4个
【解析】
【知识点】①函数图像及运用;②对数函数的定义与性质;③一元二次函数的定义与性质;④函数零点的定义与性质;⑤判断命题真假的基本方法。
【解题思路】根据对数函数和一元二次函数的性质,运用函数零点的性质和判断命题真假的基本方法,对各个命题的真假进行判断确定正确结论的个数就可得出选项。
【详细解答】作出函数函数f(x)的图像如图所示,当a=4时,关于x的方程f(x)=g(x)有
四个不同的实数根,m<0,且f()=-+=>4,m<-4,存在m(-,-4)
当a=4时,使得关于x的方程f(x)=g(x)有四个不
y
同的实数根,①正确;当m[3,4]时,无
论a取何值,关于x的方程f(x)=g(x)至多有两个
不同的实数根,②错误;当x>0时,函数
0
1
x
函数h(x)=
(x)+bf(x)+c恰有三个不同的
(m>0)
零点,,,=1,0<<1,>1,
y
f()=-ln,f()=ln,且-ln=
ln,
ln+
ln=
ln.=0,.=1,
0
1
x
=1,③正确;当m=-4时,关于x的
(m<0)
方程f(x)=g(x)
有四个不同的实数根,,,,且<<<,+=-4,
+=2,
f(x)在[,]上的最大值为ln4,
f()=-ln=ln=ln4,=4,
=,3+3+5+4=3(+)+4(+)+=-12+8+=-,
sin
(3+3+5+4)=
sin(-)=
sin
=1,④正确,其中正确的结论有
①③④共3个,C正确,选C。
4、函数f(x)=
在[-,]的图像大致为(
)(2019全国高考新课标I)
A
B
C
D
【解析】
【知识点】①函数图像及运用;②函数奇偶性的定义与性质;③判断函数奇偶性的基本方法;④求函数值的基本方法。
【解题思路】根据函数奇偶性的性质和判断函数奇偶性的基本方法,结合问题条件得到函数f(x)=
是奇函数,排除A;运用求函数值的基本方法求出f(),f()的函数值,排除B,C就可得出选项。
【详细解答】f(-x)=
==-=-
f(x),函数f(x)是奇函数,排除A;
f()==>1,f()==>0,排除B,
C,D正确,选D。
1,x>0,
5、定义符号函数sgnx=
0,x=0,则函数f(x)=sinx.sgnx的图像大致是(
)(2018成都市高三三诊)
-1,x<0
【解析】
【考点】①正弦三角函数的图像与性质;②函数图像及运用;③符号函数的定义与性质;④函数奇偶性的定义与性质;⑤判断函数奇偶性的基本方法;⑥求函数值的基本方法。
【解题思路】根据正弦三角函数和符号函数的性质,运用函数奇偶性的性质和判断函数奇偶性的基本方法,结合问题条件得到函数f(x)是偶函数,排除A;求出f(-),f()的值C,D就可得出选项。
【详细解答】
f(-x)=
sin(-x).sgn(-x)=sinx.sgnx,函数f(x)是偶函数,排除A;
f(-)=sin(-).sgn(-)=(-1).(-1)=1,f()==sin().sgn()=(-1).1=-1,选项,C,D错误可排除,
B正确,选B。
6、函数y=-++2的图像大致为(
)(2018全国高考新课标III卷)
【解析】
【考点】①函数图像及运用;②数学换元法及运用;③一元二次函数的定义与性质;④求函数值的基本方法。
【解题思路】根据数学换元法和一元二次函数的性质得到函数y图像的对称轴为x=
,排除A,C;运用求函数值的基本方法,求出x=0时,函数y的值,排除B就可得出选项。
【详细解答】设t=,
函数f(t)=-
+t+2图像的对称轴为t=,函数y=-++2的图像的对称轴为x=
,排除A,C;当
x=0时,y=-0+0+2=2>0,排除B,D正确,选D。
『思考问题4』
(1)【典例4】是近几年考试试题,归结起来主要包括:①函数图像的作法;②函数图像的认识;③函数图像的运用等几种类型;
(2)解答这类问题的基本方法是:①归结问题条件确定问题的类型;②根据问题类型的结构特征确定解答的基本方法;③按照②中确定解答的基本方法解答问题。
〔练习4〕解答下列问题:
1、函数y=
的部分图像大致为(
)(2017全国高考新课标I卷)(答案C)
2、函数y=1+x+的部分图像大致为(
)(2017全国高考新课标III卷)(答案D)
t
O
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
函数图像问题的类型与解法
理解函数图像的定义,掌握函数图像的基本作法是学习函数知识的基础之一,运用函数图像解答函数问题又是不可或缺的基本技能。函数图像主要包括:①函数图像的基本作法;②函数图像的识别;③函数图像的运用。纵观近几年数学的各种考试,函数图像问题主要有:①已知函数解析式,求作函数图像;②已知函数图像,确定函数解析式;③运用函数图像解答数学问题等几种类型。各种类型问题结构上具有相应的特征,解答方法也有一定的规律可寻。那么在实际解答函数图像问题时,到底应该如何抓住问题的结构特征,快捷,准确地给予解答呢?下面通过典型例题的详细解析来回答这个问题。
【典例1】解答下列问题:
y
1、已知y=f(x)的图像如右图所示,那么函数
Y=f(2-x)的图像是(
)
-2
-1
0
1
2
x
Y
y
y
y
-1
0
1
2
x
-2
-1
0
1
x
-1
0
1
2
x
-2
-1
0
1
x
A
B
C
D
【解析】
【知识点】①函数图像及运用;②函数图像平移变换的基本方法;③函数图像对称变换的基本方法。
【解题思路】根据函数图像的性质和函数图像平移变换,对称变换的基本方法,可知函数Y=f(2-x)的图像是将函数y=f(x)的图像沿Y轴对称变换,再向右平移2个单位长度后得到的图像,从而就可得出选项。
【详细解答】函数Y=f(2-x)的图像是将函数y=f(x)的图像沿Y轴对称变换,再向右平移2个单位长度后得到的图像,选项C的图像符合,C正确,选C。
2、下列函数的图像中,经过平移或翻折后不能与函数f(x)=x的图像重合的函数是(
)
A
f(x)=
B
f(x)=
x
C
f(x)=
D
f(x)=
+1
【解析】
【知识点】①函数图像及运用;②函数图像平移变换的基本方法;③函数图像翻折变换的基本方法;④指数函数的定义与性质;⑤对数函数的定义与性质。
【解题思路】根据指数函数和对数函数的性质,运用函数图像平移变换和翻折变换的基本方法,对各选项函数的图像通过平移变换或翻折变换能否得到函数f(x)=x的图像进行判断就可得出选项。
【详细解答】对A,函数f(x)=
的图像与函数f(x)=x的图像关于直线y=x对称,只需把函数f(x)=
的图像沿直线y=x翻折就可得到函数f(x)=x的图像,即A错误;对B,函数f(x)=
x的图像与函数f(x)=x的图像关于X轴对称,只需把函数f(x)=
x的图像沿X轴翻折就可得到函数f(x)=x的图像,即B错误;对C,函数f(x)=
=,无论通过怎样的平移变换或翻折变换都不能得到函数f(x)=x的图像,C正确,选C。
3、为了得到函数f(x)=lg的图像,只需把函数f(x)=lgx的图像上所有的点(
)
A
向左平移3个单位长度,再向上平移1个单位长度
B
向右平移3个单位长度,再向上平移1个单位长度
C
向左平移3个单位长度,再向下平移1个单位长度
D
向右平移3个单位长度,再向下平移1个单位长度
【解析】
【知识点】①函数图像及运用;②函数图像平移变换的基本方法;③对数的定义与性质;④对数运算性质及运用。
【解题思路】根据对数的性质和对数的运算性质,得到f(x+3)-1=lg(x+3)-lg10=
lg,运用函数图像的性质和函数图像平移变换的基本方法,可知函数函数f(x)=lgx的图像上所有的点向左平移3个单位长度,再向下平移一个单位长度能够得到函数f(x)=lg的图像,从而就可得出选项。
【详细解答】函数f(x+3)-1=
lg(x+3)-lg10=
lg,函数函数f(x)=lgx的图像上所有的点向左平移3个单位长度,再向下平移一个单位长度能够得到函数f(x)=lg的图像,
C正确,选C。
y
4、设奇函数f(x)的定义域是[-5,5],若当
x[0,5]时,f(x)的图像如图所示,则不
等式f(x)<0的解集是
;
-2
-1
0
2
5
x
【解析】
【知识点】①函数图像及运用;②奇函数的定义与性质;③求解不等式的基本方法。
【解题思路】根据奇函数的性质和函数图像,作出函数f(x)
x[-5,0]时的图像,运用函数图像和求解不等式的基本方法,结合问题条件得到关于x的不等式,求解不等式就可求出不等式f(x)<0的解集。
【详细解答】函数f(x)是奇函数,作出函数f(x)
x[-5,0]时的图像如图所示,
由图知,f(x)<0,-2
5、作出下列函数的图像:
(1)
y=|x-1|(x+1);
(2)y=
;
(3)
y=|(x+1)|;
(4)
y=;
(5)
y=
-2|x|-1;
(6)
y=3sin(2x-
)。
【解析】
【知识点】①函数图像的定义与性质;②作函数图像的基本方法。
【解题思路】根据函数图像的性质,运用作函数图像的基本方法就可作出各函数的图像。
【详细解答】(1)y=|x-1|(x+1)=
-1,x1,
(2)y==
,x0,
1-,x<1,
=,x<0,
函数y=|x-1|(x+1)的图像如图所示;
函数y=的图像如图所示;
(3)
y=|(x+1)|=
(x+1),x0,
(4)
y===2+
-(x+1),-1
函数y=|(x+1)|的图像如图所示;
函数y=的图像如图所示;
(5)y=
-2|x|-1=-2x-1,x0,
(6)y=3sin(2x-
)=3sin[2(x-
)],
+2x-1,x<0,
函数y=
-2|x|-1的图像如图所示;
函数y=3sin(2x-
)的图像如图所示。
y
y
y
1
1
-1
0
1
x
-1
0
1
x
-1
0
1
x
-1
(1题图)
(2题图)
(3题图)
y
y
y
2
1
1
-1
0
1
x
-1
0
1
x
-1
0
1
x
-1
-1
(4题图)
(5题图)
(6题图)
『思考问题1』
(1)【典例1】是求作函数图像的问题,这类问题主要包括:①已知函数解析式,求作函数图像;②函数图像的平移变换;③函数图像的伸缩变换;④函数图像的对称变换;⑤函数图像的翻折变换;⑥函数图像的旋转变换;解答这类问题需要理解函数图像的定义,掌握函数图像的基本作法;函数图像的基本方法有:①直接作图法;②描点作图法;③图像变换法;
(2)面对问题应该选用哪种作图方法,需根据题给条件和所求问题来确定;
(3)应用图像变换法作图需要熟练掌握几种基本函数(一次函数,二次函数,反比例函数,指数函数,对数函数,幂函数,正弦函数,余弦函数)的图像,注意图像变换的顺序。
〔练习1〕解答下列问题:
1、函数f(x)=1+x与g(x)=
在同一直角坐标系中的图像大致是(
)(答案C)
y
2
y
2
y
2
y
2
1
1
1
1
0
1
2
x
0
1
2
x
0
1
2
x
0
1
2
x
A
B
C
D
2、作出下列函数的图像:
(1)
y=;
(2)
y=;
(3)
y=
;
(4)
y=;(5)
y=3sin(2x+);
(6)
y=|x-1|
;
(7)
y=|x-2|.(x+1)。(答案)
(1)
y
(2)
y
(3)
y
1
1
-1
0
1
x
0
x
-3
-2
-1
0
x
-1
(4)y
(5)
y
(6)
y
2
1
1
0
1
x
-
0
0
1
2
x
(7)
y
0
1
2
x
【典例2】解答下列问题:
1、函数f(x)=ln(+1)的图像大致是(
)
【解析】
【知识点】①对数函数的定义,图像与性质;②函数图像及运用;③作函数图像的基本方法。
【解题思路】根据对数函数的性质和图像,运用作函数图像的基本方法,由f(0)=ln(0+1)=0,可以排除B,D,由
f(-x)=
=ln[+1]=
=ln(+1)=
f(x),得到函数f(x)是偶函数,可以排除C,从而就可得出选项。
【详细解答】函数f(x)=ln(+1)的定义域为R,f(0)=ln(0+1)=0,可以排除B,D,ff(-x)=
=ln[+1]=
=ln(+1)=
f(x),函数f(x)是偶函数,可以排除C,A正确,选A。
y
2、右图中的图像所表示的函数的解析式为(
)
-----------|
A
y=|x-1|
(0≤x≤2)
B
y=-|x-1|(0≤x≤2)
|
C
y=-|x-1|
(0≤x≤2)
D
y=1-|x-1|
(0≤x≤2)
0
1
2
x
【解析】
【知识点】①函数图像及运用;②根据函数图像确定函数解析式的基本方法。
【解题思路】根据函数图像,
f(0)
=0,可以排除A,C,
f(1)=
,可以排除D,从而就可得出选项。
【详细解答】由函数f(x)的图像得:f(0)
=0,对A,f(0)=
|0-1|=,对C,f(0)=
-|0-1|=
-1=,排除A,C;
f(1)=
,对D,f(1)=1-|0-1|=1-1=0,排除D,B正确,选B。
3、已知函数y=f(x)的大致图像如图所示,则函数
y
y=f(x)的解析式可能为(
)
A
f(x)=
lnx
B
f(x)=
ln|x|
C
f(x)=
ln|x|
D
f(x)=
ln|x|
0
x
【解析】
【知识点】①函数图像及运用;②根据函数图像确定函数解析式的基本方法。
【解题思路】根据函数图像,可知函数f(x)的定义域为(-
,0)(0,+
),可排除A;由函数f(x)在(-
,0)上单调递减,在(0,+
)上单调递增,可排除B;函数y=f(x)不是偶函数,可以排除D,从而就可得出选项。
【详细解答】根据函数图像,可知函数f(x)的定义域为(-
,0)(0,+
),可排除A;函数f(x)在(-
,0)上单调递减,在(0,+
)上单调递增,可排除B;函数f(x)不是偶函数,
可以排除D,C正确,选C。
4、函数f(x)=
的图像大致为(
)
y
y
y
y
1
1
1
1
0
1
x
0
1
x
0
1
x
0
1
x
A
B
C
D
【解析】
【知识点】①函数图像及运用;②根据函数图像确定函数解析式的基本方法。
【解题思路】根据函数f(x)=
=1+=1+,可知函数f(x)的定义域为(-
,0)(0,+
),可排除C,D,由当x>0时,函数f(x)=
1+单调递减,可以排除B,从而就可得出选项。
【详细解答】函数f(x=
=1+=1+的定义域为(-
,0)(0,+
),排除C,D;当x>0时,函数f(x)=
1+单调递减,
排除B,A正确,选A。
5、如图已知,圆心在上,半径为1m的圆O在t=0时与相切于点A,圆O沿以1m/s的速度匀速向上移动,圆被直线所截上方圆弧长记为x,令y=cosx,则y与时间t(0≤t≤1,单位:s)的函数y=f(t)的图像大致为()
A
B
C
D
【解析】
【知识点】①函数图像及运用;②圆的定义与性质;③余弦三角函数的定义,性质与图像。
【解题思路】根据圆和余弦三角函数的性质,得到cos==1-t,从而得到y=cosx=2-1(0≤t≤1),确定出函数y=f(t)的图像就可得出选项。
【详细解答】如图,
cos==1-t,
y=f(t)
=
cosx=2-1,
f(0)=2-1=1,f(1)=0-1=-1,
B选项的图像符合题意,B正确,选B。
『思考问题2』
(1)
【典例2】是函数图像的识图与辨图问题,这类问题常见的类型有:①已知函数图像,确定函数解析式选;②已知函数解析式,确定函数的图像;
(2)已知函数图像,确定函数解析式的基本方法是:①从图像的左右,上下分布观察函数定义域域和函数的值域;②
从图像的变化趋势观察函数的单调性;③
从图像的对称性观察函数的奇偶性;④从图像的循环往复观察函数的周期性;
(3)已知函数的解析式,确定函数图像的基本方法是:①从函数的定义域判断图像的左右位置,从函数的值域判断图像上下位置;②从函数的单调性,判断图像的变化趋势;③从函数的奇偶性,判断图像的对称性;④从函数的周期性,判断图像的循环往复;⑤从函数的极值点判断函数的最值点。
〔练习2〕解答下列问题:
y
1、已知函数y=f(x)的图像如右图,求函数
Y=f(x)的解析式。(答案f(x)=|x|-1)
-1
0
1
x
2、若函数f(x)=sinax+b(x>0),的图像如图所示,则函数g(x)=
(x+b)的图像可能是(
)
y
y
y
y
y
1
1
1
1
1
0
2
3
x
0
1
2
3
x
0
1
2
3
x
0
1
2
3
x
0
1
2
3
x
-1
-1
A
-1
B
-1
C
-1
D(答案C)
3、已知函数y=f(x)和函数y=g(x)的图像如图(1),
y
y
(2)所示,则函数F(x)=f(x).g(x)的图像可能
是(
)(答案A)
0
x
0
x
y
y
y
(1)
y
(2)
0
x
0
x
0
x
0
x
A
B
C
D
4、已知lga+lgb=0,则函数f(x)=与函数g(x)=
(x+b)的图像可能是(
)(答案B)
y
y
y
y
1
1
1
1
0
1
x
0
1
x
0
1
x
0
1
x
A
B
C
D
5、已知函数f(x)=
,则y=f(x)的图像大致为(
)(答案C)
y
y
y
y
1
1
1
0
1
x
1
0
1
x
0
1
x
0
1
x
A
B
C
D
6、函数f(x)=-xcosx的部分图像是(
)(答案B)
y
y
y
y
0
x
0
x
0
x
0
x
A
B
C
D
【典例3】解答下列问题:
y
1、已知f(x)=a+b+cx+d的图像如图所示,则(
)
0
1
2
x
A
b
(-∞,0)
B
b
(0,1)
C
b
(1,2)
D
b
(2,+∞)
【解析】
【知识点】①函数图像及运用;②函数零点的定义与性质;③运用函数图像确定函数解析式中参数取值范围的基本方法。
【解题思路】根据函数图像和函数零点的性质,得到关于a,b,c,d
的方程组,求解方程组求出a,c,d关于参数b的表示式,从而得到函数f(x)只含参数b的解析式,运用函数图像确定参数b的取值范围就可得出选项。
【详细解答】f(0)=0+0+0+d=0①,f(1)=a+b+c+d=0②,f(2)=8a+4b+2c+d=0③,联立①②③解得:a=-,c=-,d=0,f(x)=-
+b-x=-x(-3x+2)=
-x(x-1)(x-2),
x>2时,f(x)>0恒成立,
->0,即b<0,A正确,选A。
2、若函数f(x)的反函数为(x),则函数f(x-1)与函数(x-1)的图像可能是(
)
2
y
2
y
2
y
2
y
1
1
1
1
0
1
2
x
0
1
2
x
0
1
2
x
0
1
2
x
A
B
C
D
【解析】
【知识点】①函数图像及运用;②函数反函数的定义与性质;③指数函数的定义与性质;④对数函数的定义与性质;⑤函数图像平移变换的基本方法。
【解题思路】根据函数反函数,指数函数和对数函数的性质,结合图像得到指数函数和对数函数的底数都大于1,运用函数图像平移变换的基本方法确定出符合题意的图像就可得出选项。
【详细解答】指数函数与对数函数互为反函数,由图知指数函数和对数函数的底数都大于1,函数f(x-1)与函数(x-1)的图像是由函数f(x)与函数(x)的图像向右平移一个单位长度而得到,可以排除A,C,D,B正确,选B。
3、已知函数y=f(x)的图像是下列四个图像之一,且其导函数y=(x)的图像如图所示,则该函数的图像是(
)
【解析】
【知识点】①函数图像及运用;②函数导函数的定义与性质;③运用函数导函数判断函数单调性的基本方法。
【解题思路】根据函数导函数的图像和运用函数导函数判断函数单调性的基本方法,得到函数y=f(x)在(-1,1)上单调递增,且在(-1,0)上增长速度越来越快,在(0,1)上增长速度越来越慢,可以排除A,C,D,从而就可得出选项。
【详细解答】由导函数y=(x)的图像可知,函数y=f(x)在(-1,1)上单调递增,且在(-1,0)上增长速度越来越快,在(0,1)上增长速度越来越慢,可以排除A,C,D,B正确,选B。
4、已知函数y=f(x)的周期为2,当x[-1,1]时,f(x)=
,那么函数y=f(x)的图像与函数y=|lgx|的图像的交点共有(
)
A
10个
B
9个
C
8个
D
1个
【解析】
【知识点】①函数图像及运用;②周期函数的定义与性质;③对数函数的定义与性质。
【解题思路】根据周期函数和对数函数的性质,运用作函数图像的基本方法,在同一直角坐标系中作出函数y=f(x)和函数y=|lgx|的图像,由图像确定两个函数图像的交点的个数就可得出选项。
lgx,x1,
y
【详细解答】
y=|lgx|=
-lgx,0
,在同
1
一直角坐标系中作出函数y=f(x)和函数y=|lgx|的图
-1
0
1
2
x
像如图所示,由图知函数y=f(x)的图像与函数y=|lgx|的图像的交点共有10个,A正确,选A。
5、已知函数y=
的图像与函数y=kx的图像恰有两个交点,则实数k的取值范围是
;
【解析】
【知识点】①函数图像及运用;②绝对值的定义与性质;③一元一次函数的定义与性质;④分段函数的定义与性质;⑤求函数解析式中参数取值范围的基本方法。
【解题思路】根据绝对值的性质,把函数y=
化为分段函数,运用分段函数,一元一次函数的性质和已知函数解析式作函数图像的基本方法,在同一直角坐标系中作出函数y=
,函数y=kx的图像,利用函数图像就可求出实数k的取值范围。
【详细解答】函数y=
=x+1,x<-1或x>1,
y
-x-1,-1≤x<1,在同一直角坐
标系中作出函数y=
,函数y=kx的图像如图所示,
-1
0
1
x
由图知,-1<-k<0,或-2<-k<-1,0<k<1或1<k<2,若函数y=
的图像与函数y=kx的图像恰有两个交点,则实数k的取值范围是(0,1)(1,2)。
6、如图,|OA|=2(单位:m),|OB|=1(单位:m),
D
OA与OB的夹角为,以A为圆心,AB为半径
B
作圆弧BDC与线段OA延长线交于点C,甲,乙
0
A
C
两质点同时从点O出发,甲先以速率1(单位:m/s)沿线段OB行至点B,再以速率3(单位:m/s)沿圆弧BDC行至点C后停止;乙以速率2(单位:m/s)沿线段OA行至点A后停止,设t时刻甲,乙所到达的两点连线与它们经过的路径所围成的面积为S(t)(S(0)=0),则函数y=S(t)的图像大致是(
)
y
y
y
y
0
x
0
x
0
x
0
x
A
B
C
D
【解析】
【知识点】①函数图像及运用;②求函数解析式的基本方法;③三角形面积公式及运用;④扇形面积公式及运用。
【解题思路】根据三角形面积公式,扇形面积公式和求函数解析式的基本方法,结合时间点1求出t时刻甲、乙所到达的两点连线与它们经过的路径所围成的面积S(t)的解析式,运用函数解析式确定出函数S(t)的图像就可得出选项。
【详细解答】①当0≤t≤1时,
S(t)=
t.2tsin=;②1<1≤(为甲质点到达点C所需的时间)时,S(t)=
+3|AB|(t-1)=+(t-1);③当t>时,S(t)为一个常数,可以排除C;函数S(t)在[0,1]上单调递增,且函数图像是向下凸的,可以排除B,D,A正确,选A。
7、若关于x的不等式>x+m的解为-≤x<4,求实数m的值。
【解析】
【知识点】①函数图像及运用;②幂函数的定义与性质;③求解不等式的基本方法;④求函数解析式中参数值的基本方法。
【解题思路】根据幂函数和一元一次函数的性质,运用已知函数解析式作函数图像的基本方法在同一直角坐标系中作出函数f(x)=
,函数g(x)=x+m的图像,运用函数图像就可求出实数m的值。
y
【详细解答】在同一直角坐标系中作出函数
1
f(x)=
,函数g(x)=x+m的图像如图
-0
4
x
所示,关于x的不等式>x+m的解为-≤x<4,由图知函数f(x)与函数g(x)的图像相交于点(4,3),f(4)==3=g(4)=4+m,
m=-1,若关于x的不等式>x+m的解为-≤x<4,则实数m的值为-1。
『思考问题3』
(1)【典例3】是函数图像的运用问题,这类问题主要包括:①运用函数图像研究函数的性质;②运用函数图像求解不等式;③运用函数图像求函数的零点;
(2)解答函数图像运用问题的常用方法是:①定性分析法;②定量分析法;③函数模型法。
〔练习3〕解答下列问题:
1、已知函数f(x)=
(a>0,且a≠0)在同一直角坐标系中(x)与y=的图像可能是(
)(答案C)
2
y
2
y
2
y
2
y
1
--|
1
---
|
1
---
|
1
---
|
|
|
|
|
-10
1
2
x
-1
0
1
2
x
-1
0
1
2
x
-1
0
1
2
x
A
B
C
D
2、如果函数f(x)=
+的图像沿x轴向右平移a个单位得到曲线C,设曲线C的方程为y=g(x),对任意xR,都有g(1+x)=-g(1-x),试求g(1)+g(-1)的值。(答案-8-)
3、a为何值时,方程lg(3-x)+lg(x-1)=lg(a-x)有两解,一解,无解?(答案当3
【考题演练】
【典例4】解答下列问题:
1、函数f(x)=cosx.ln(-x)在[-1,1]的图像大致为(
)(2020成都市高三二诊)
【解析】
【知识点】①函数图像及运用;②函数奇偶性的定义与性质;③判断函数奇偶性的基本方法;④函数单调性的定义与性质;⑤判断函数单调性的基本方法。
【解题思路】根据函数奇偶性的性质和判断函数奇偶性的基本方法,得到函数f(x)是奇函数,运用函数单调性的性质和判断函数单调性的基本方法,得到函数f(x)
在[0,1]上单调递增,从而确定函数f(x)=cosx.ln(-x)在[-1,1]的图像大致就可得出选项。
【详细解答】
f(-x)=cos(-x).ln(+x)=
cosx
ln(+x)=
cosx
ln[(+x)
.
]=
cosx
ln()=cosx
ln()=-cosx.ln(-x)=-
f(x),函数f(x)是奇函数,排除C,D;当x[0,1]时,函数y=
cosx单调递减,函数y=ln
(-x)单调递增,函数f(x)
在[0,1]上单调递减,排除A,B正确,选B。
2、函数y=
在[-6,6]的大致图像为(
)(2019全国高考新课标III(理))
A
B
C
D
【解析】
【知识点】①函数图像及运用;②函数奇偶性的定义与性质;③判断函数奇偶性的基本方法;④求函数值的基本方法。
【解题思路】根据函数奇偶性的性质和判断函数奇偶性的基本方法,结合问题条件得到函数y=
是奇函数,排除C;运用求函数值的基本方法求出当x=6时的函数值y=7>0,排除A,D就可得出选项。
【详细解答】设f(x)=
,函数f(x)的定义域为R关于原点对称,f(-x)
=
=-=-
f(x),函数f(x)是奇函数,排除C;
f(6)=
=
=7,排除A,D,B正确,选B。
3、已知函数f(x)=
|lnx|,x>0,和g(x)=a(aR且为常数),有以下结论:①当a=4时,
-+mx,x0,存在实数m,使得关于x的方程f(x)=g(x)有四个不
同的实数根;②存在m[3,4],使得关于x的方程f(x)=g(x)有三个不同的实数根;③当
x>0时,若函数h(x)=
(x)+bf(x)+c恰有三个不同的零点,,,则=1;
④当m=-4时,关于x的方程f(x)=g(x)
有四个不同的实数根,,,,且<
<<,若f(x)在[,]上的最大值为ln4,则sin(3+3+5+4)=1,
其中正确结论的个数是(
)(2018—2019成都市高一上期调研考试)
A
1个
B
2个
C
3个
D
4个
【解析】
【知识点】①函数图像及运用;②对数函数的定义与性质;③一元二次函数的定义与性质;④函数零点的定义与性质;⑤判断命题真假的基本方法。
【解题思路】根据对数函数和一元二次函数的性质,运用函数零点的性质和判断命题真假的基本方法,对各个命题的真假进行判断确定正确结论的个数就可得出选项。
【详细解答】作出函数函数f(x)的图像如图所示,当a=4时,关于x的方程f(x)=g(x)有
四个不同的实数根,m<0,且f()=-+=>4,m<-4,存在m(-,-4)
当a=4时,使得关于x的方程f(x)=g(x)有四个不
y
同的实数根,①正确;当m[3,4]时,无
论a取何值,关于x的方程f(x)=g(x)至多有两个
不同的实数根,②错误;当x>0时,函数
0
1
x
函数h(x)=
(x)+bf(x)+c恰有三个不同的
(m>0)
零点,,,=1,0<<1,>1,
y
f()=-ln,f()=ln,且-ln=
ln,
ln+
ln=
ln.=0,.=1,
0
1
x
=1,③正确;当m=-4时,关于x的
(m<0)
方程f(x)=g(x)
有四个不同的实数根,,,,且<<<,+=-4,
+=2,
f(x)在[,]上的最大值为ln4,
f()=-ln=ln=ln4,=4,
=,3+3+5+4=3(+)+4(+)+=-12+8+=-,
sin
(3+3+5+4)=
sin(-)=
sin
=1,④正确,其中正确的结论有
①③④共3个,C正确,选C。
4、函数f(x)=
在[-,]的图像大致为(
)(2019全国高考新课标I)
A
B
C
D
【解析】
【知识点】①函数图像及运用;②函数奇偶性的定义与性质;③判断函数奇偶性的基本方法;④求函数值的基本方法。
【解题思路】根据函数奇偶性的性质和判断函数奇偶性的基本方法,结合问题条件得到函数f(x)=
是奇函数,排除A;运用求函数值的基本方法求出f(),f()的函数值,排除B,C就可得出选项。
【详细解答】f(-x)=
==-=-
f(x),函数f(x)是奇函数,排除A;
f()==>1,f()==>0,排除B,
C,D正确,选D。
1,x>0,
5、定义符号函数sgnx=
0,x=0,则函数f(x)=sinx.sgnx的图像大致是(
)(2018成都市高三三诊)
-1,x<0
【解析】
【考点】①正弦三角函数的图像与性质;②函数图像及运用;③符号函数的定义与性质;④函数奇偶性的定义与性质;⑤判断函数奇偶性的基本方法;⑥求函数值的基本方法。
【解题思路】根据正弦三角函数和符号函数的性质,运用函数奇偶性的性质和判断函数奇偶性的基本方法,结合问题条件得到函数f(x)是偶函数,排除A;求出f(-),f()的值C,D就可得出选项。
【详细解答】
f(-x)=
sin(-x).sgn(-x)=sinx.sgnx,函数f(x)是偶函数,排除A;
f(-)=sin(-).sgn(-)=(-1).(-1)=1,f()==sin().sgn()=(-1).1=-1,选项,C,D错误可排除,
B正确,选B。
6、函数y=-++2的图像大致为(
)(2018全国高考新课标III卷)
【解析】
【考点】①函数图像及运用;②数学换元法及运用;③一元二次函数的定义与性质;④求函数值的基本方法。
【解题思路】根据数学换元法和一元二次函数的性质得到函数y图像的对称轴为x=
,排除A,C;运用求函数值的基本方法,求出x=0时,函数y的值,排除B就可得出选项。
【详细解答】设t=,
函数f(t)=-
+t+2图像的对称轴为t=,函数y=-++2的图像的对称轴为x=
,排除A,C;当
x=0时,y=-0+0+2=2>0,排除B,D正确,选D。
『思考问题4』
(1)【典例4】是近几年考试试题,归结起来主要包括:①函数图像的作法;②函数图像的认识;③函数图像的运用等几种类型;
(2)解答这类问题的基本方法是:①归结问题条件确定问题的类型;②根据问题类型的结构特征确定解答的基本方法;③按照②中确定解答的基本方法解答问题。
〔练习4〕解答下列问题:
1、函数y=
的部分图像大致为(
)(2017全国高考新课标I卷)(答案C)
2、函数y=1+x+的部分图像大致为(
)(2017全国高考新课标III卷)(答案D)
t
O
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
