1.1 反比例函数同步练习(含答案)
文档属性
| 名称 | 1.1 反比例函数同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 996.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-28 15:28:48 | ||
图片预览




文档简介
1.1 反比例函数
一、选择题
1.下列函数中,y是x的反比例函数的是( )
A.y=
B.y=
C.y=
D.y=+2
2.若函数y=(m+1)x|m|-2是反比例函数,则m=( )
A.±1
B.±3
C.-1
D.1
3.下列各问题中,两个变量之间的关系不是反比例函数的是( )
A.某工程队完成500
m挖渠时,时间t(天)与该工程队挖渠的平均速度v(m/天)之间的关系
B.菱形的面积为36
cm2,它的两条对角线的长y(cm)与x(cm)之间的关系
C.一个玻璃容器的体积为30
L时,所盛液体的质量m与所盛液体的体积V之间的关系
D.压力为600
N时,压强p与受力面积S之间的关系
4.下列函数:①y=;②3xy=1;③y=;④y=.其中反比例函数有( )
A.4个
B.3个
C.2个
D.1个
5.已知y是x的反比例函数,且常数k=,则该函数的表达式是( )
A.y=x
B.y=
C.y=
D.y=
6.【2020·德阳】已知函数y=当函数值为3时,自变量x的值为( )
A.-2
B.-
C.-2或-
D.-2或-
7.【中考·滨州】如图,在平面直角坐标系中,菱形OABC的边OA在x轴的正半轴上,反比例函数y=(x>0)的图象经过对角线OB的中点D和顶点C.若菱形OABC的面积为12,则k的值为( )
A.6
B.5
C.4
D.3
8.下列各组的两个变量间满足反比例关系的是( )
A.三角形面积一定时,它的一边长与该边上的高
B.等腰三角形的周长一定时,它的底边长与腰长
C.圆的周长与它的半径
D.圆的面积与它的半径
9.【中考·广州】一司机驾驶汽车从甲地去乙地,他以平均80千米/时的速度用了4小时到达乙地,当他按原路匀速返回时,汽车的速度v(千米/时)与时间t(小时)的函数关系式是( )
A.v=320t
B.v=
C.v=20t
D.v=
10.【2020·长沙】2019年10月,《长沙晚报》对外发布长沙高铁西站设计方案.该方案以“三湘四水,杜娟花开”为设计理念,塑造出“杜娟花开”的美丽姿态.该高铁站建设初期需要运送大量土石方.某运输公司承担了运送总量为106
m3土石方的任务,该运输公司平均运送土石方的速度v(单位:m3/天)与完成运送任务所需时间t(单位:天)之间的函数表达式是( )
A.v=
B.v=106t C.v=t2 D.v=106t2
二、填空题
11.一般地,如果两个变量y与x的关系可以表示成y=(k为常数,k≠0)的形式,那么称y是x的__________函数,其中x是自变量,常数k(k≠0)称为反比例函数的比例系数.反比例函数的自变量取值范围是___________.反比例函数y=(k≠0)的表达式还可以表示为:①xy=k;②y=kx-1.
12.已知y与x成反比例关系,且当x=-3时,y=4,则当x=6时,y的值为________.
13.如果关于x,y的反比例函数的表达式为y=,那么m的值为________.
14.已知函数y=(a+1)x|2a|-1.
(1)当a=________时,y是x的正比例函数,函数表达式为________;
(2)当a=________时,y是x的反比例函数,函数表达式为________.
三、解答题
15.在下列函数关系式中,哪些函数表示y是x的反比例函数?
(1)y=;(2)y=;(3)y=;(4)xy=;(5)y=;(6)y=-;(7)y=2x-1;(8)y=(a≠5,a是常数).
16.若y=(m+2)xm-5为反比例函数,求反比例函数的表达式.
17.有一个面积为30的梯形,其上底长是下底长的一半,设下底长为x,高为y,求y关于x的函数表达式.这个函数是反比例函数吗?若是,请指出比例系数;若不是,请判断函数类型.
18.李贝说:“在如图所示的矩形ABCD中,AB=6,BC=8,P是BC边上一动点,连接AP,过点D作DE⊥AP于点E.设AP=x(6≤x≤10),DE=y,则y是x的反比例函数.”你认为李贝说得对吗?请给出证明.
19.已知y=y1+y2,y1与x2成正比例函数关系,y2与x成反比例函数关系,且当x=1时,y=3;当x=-1时,y=1.
(1)求y与x之间的函数表达式;
(2)当x=-时,求y的值.
20.某厂仓库储存了部分原料,按原计划每小时消耗2
t,可用60
h.由于技术革新,实际生产能力有所提高,即每小时消耗的原料量大于计划消耗的原料量.设现在每小时消耗原料x(单位:t),库存的原料可使用的时间为y(单位:h).
(1)写出y关于x的函数表达式,并求出自变量的取值范围;
(2)若恰好经过24
h才有新的原料进厂,为了使机器不停止运转,则x应控制在什么范围内?
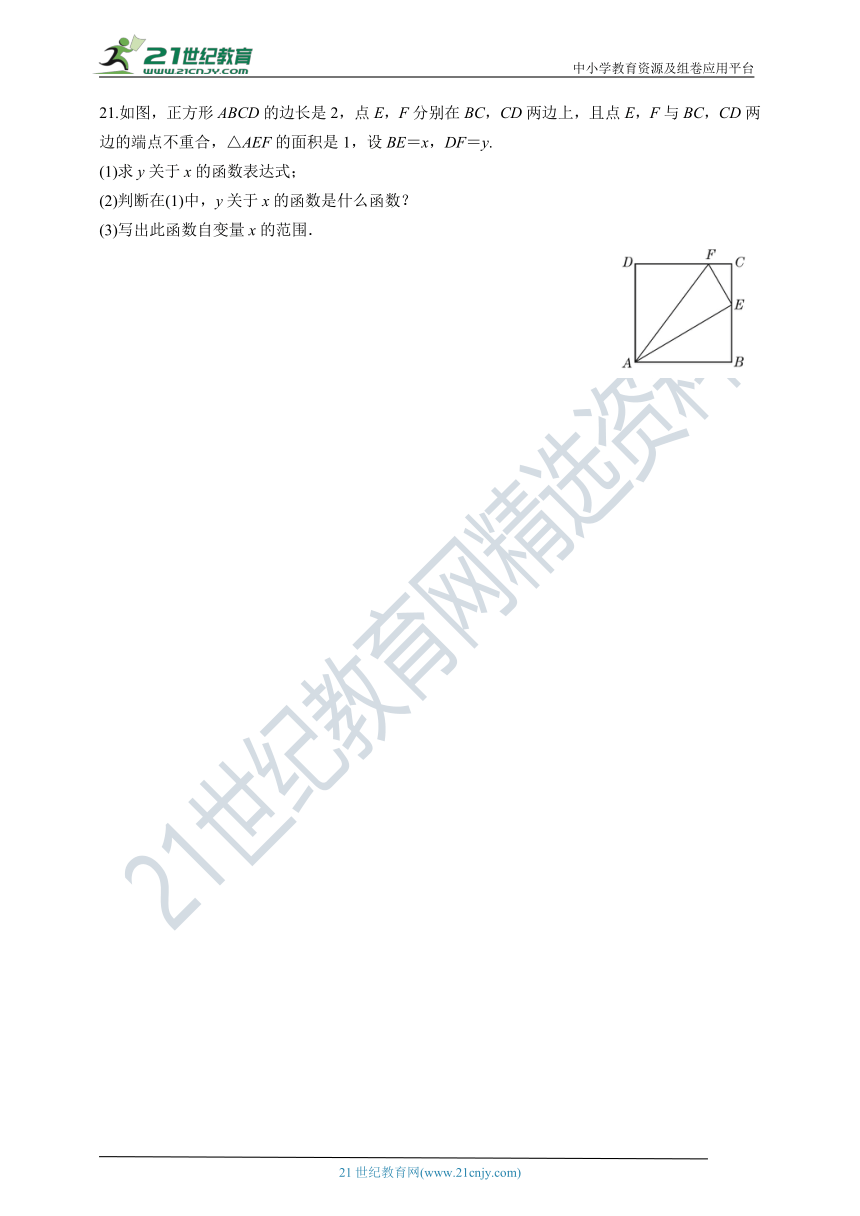
21.如图,正方形ABCD的边长是2,点E,F分别在BC,CD两边上,且点E,F与BC,CD两边的端点不重合,△AEF的面积是1,设BE=x,DF=y.
(1)求y关于x的函数表达式;
(2)判断在(1)中,y关于x的函数是什么函数?
(3)写出此函数自变量x的范围.
中小学教育资源及组卷应用平台
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.下列函数中,y是x的反比例函数的是( B )
A.y=
B.y=
C.y=
D.y=+2
2.若函数y=(m+1)x|m|-2是反比例函数,则m=( D )
A.±1
B.±3
C.-1
D.1
3.下列各问题中,两个变量之间的关系不是反比例函数的是( C )
A.某工程队完成500
m挖渠时,时间t(天)与该工程队挖渠的平均速度v(m/天)之间的关系
B.菱形的面积为36
cm2,它的两条对角线的长y(cm)与x(cm)之间的关系
C.一个玻璃容器的体积为30
L时,所盛液体的质量m与所盛液体的体积V之间的关系
D.压力为600
N时,压强p与受力面积S之间的关系
4.下列函数:①y=;②3xy=1;③y=;④y=.其中反比例函数有( B )
A.4个
B.3个
C.2个
D.1个
5.已知y是x的反比例函数,且常数k=,则该函数的表达式是( B )
A.y=x
B.y=
C.y=
D.y=
6.【2020·德阳】已知函数y=当函数值为3时,自变量x的值为( A )
A.-2
B.-
C.-2或-
D.-2或-
【解析】若x<2,当y=3时,-x+1=3,
解得x=-2;
若x≥2,当y=3时,-=3,
解得x=-,不合题意,舍去;∴x=-2.
7.【中考·滨州】如图,在平面直角坐标系中,菱形OABC的边OA在x轴的正半轴上,反比例函数y=(x>0)的图象经过对角线OB的中点D和顶点C.若菱形OABC的面积为12,则k的值为( )
A.6
B.5
C.4
D.3
【解析】设点A的坐标为(a,0),点C的坐标为,则点D的坐标为.
∴解得k=4.
8.下列各组的两个变量间满足反比例关系的是( )
A.三角形面积一定时,它的一边长与该边上的高
B.等腰三角形的周长一定时,它的底边长与腰长
C.圆的周长与它的半径
D.圆的面积与它的半径
【解析】A选项中设三角形面积为S,一边长为a,该边上的高为h,则有a=;B选项中设三角形的周长为C,底边长为a,腰长为b,则有a=C-2b;
C选项中设圆的周长为C,半径为r,则有C=2πr;
D选项中设圆的面积为S,半径为r,则有S=πr2.观察可得,只有A选项中的两个变量间满足反比例关系.
9.【中考·广州】一司机驾驶汽车从甲地去乙地,他以平均80千米/时的速度用了4小时到达乙地,当他按原路匀速返回时,汽车的速度v(千米/时)与时间t(小时)的函数关系式是( B )
A.v=320t
B.v=
C.v=20t
D.v=
10.【2020·长沙】2019年10月,《长沙晚报》对外发布长沙高铁西站设计方案.该方案以“三湘四水,杜娟花开”为设计理念,塑造出“杜娟花开”的美丽姿态.该高铁站建设初期需要运送大量土石方.某运输公司承担了运送总量为106
m3土石方的任务,该运输公司平均运送土石方的速度v(单位:m3/天)与完成运送任务所需时间t(单位:天)之间的函数表达式是( A )
A.v=
B.v=106t C.v=t2 D.v=106t2
【点拨】∵运送土石方的总量=平均运送土石方的速度v×完成运送任务所需时间t,
∴106=vt.∴v=.
二、填空题
11.一般地,如果两个变量y与x的关系可以表示成y=(k为常数,k≠0)的形式,那么称y是x的__________函数,其中x是自变量,常数k(k≠0)称为反比例函数的比例系数.反比例函数的自变量取值范围是___________.反比例函数y=(k≠0)的表达式还可以表示为:①xy=k;②y=kx-1.
【答案】反比例;所有非零实数
12.已知y与x成反比例关系,且当x=-3时,y=4,则当x=6时,y的值为________.
【点拨】设反比例函数的表达式为y=(k≠0),
∵当x=-3时,y=4,∴4=,解得k=-12.
∴反比例函数的表达式为y=.
∴当x=6时,y==-2.
13.如果关于x,y的反比例函数的表达式为y=,那么m的值为________.
【点拨】∵反比例函数的表达式为y=,∴
∴|m|=3且m≠-3.∴m=3.
14.已知函数y=(a+1)x|2a|-1.
(1)当a=________时,y是x的正比例函数,函数表达式为________;
(2)当a=________时,y是x的反比例函数,函数表达式为________.
【答案】1
y=2x
0
y=
三、解答题
15.在下列函数关系式中,哪些函数表示y是x的反比例函数?
(1)y=;(2)y=;(3)y=;(4)xy=;(5)y=;(6)y=-;(7)y=2x-1;(8)y=(a≠5,a是常数).
【点拨】根据反比例函数的概念,必须是形如y=(k是常数,且k≠0)的函数,才是反比例函数.如(2),(3),(6),(8)均符合这一概念的要求,所以它们都是反比例函数.但还要注意y=(k是常数,且k≠0)常见的变化形式,如xy=k,y=kx-1等,所以(4),(7)也是反比例函数.对于(5),y是(x-1)的反比例函数,而不是x的反比例函数.(1)中y是x的正比例函数.故(2)(3)(4)(6)(7)(8)是表示y是x的反比例函数.
16.若y=(m+2)xm-5为反比例函数,求反比例函数的表达式.
解:∵y=(m+2)xm-5为反比例函数,
∴m-5=-1且m+2≠0,解得m=4.
∴反比例函数的表达式为y=.
17.有一个面积为30的梯形,其上底长是下底长的一半,设下底长为x,高为y,求y关于x的函数表达式.这个函数是反比例函数吗?若是,请指出比例系数;若不是,请判断函数类型.
解:由题意得y×=30,则y=,故这个函数是反比例函数,比例系数是40.
18.李贝说:“在如图所示的矩形ABCD中,AB=6,BC=8,P是BC边上一动点,连接AP,过点D作DE⊥AP于点E.设AP=x(6≤x≤10),DE=y,则y是x的反比例函数.”你认为李贝说得对吗?请给出证明.
解:李贝说得对.证明如下:
连接DP.
∵四边形ABCD是矩形,
∴AD=BC=8,AB⊥AD,AD∥BC.
∴AB与△ADP的AD边上的高等长.
∴S△ADP=AD·AB=×8×6=24.
又S△ADP=AP·DE=xy,
∴xy=48.
∴y=(6≤x≤10),
即y是x的反比例函数.
19.已知y=y1+y2,y1与x2成正比例函数关系,y2与x成反比例函数关系,且当x=1时,y=3;当x=-1时,y=1.
(1)求y与x之间的函数表达式;
解:设y1=k1x2,y2=(k1≠0,k2≠0),则y=k1x2+.
将x=1,y=3和x=-1,y=1分别代入,
得解得
∴y与x之间的函数表达式为y=2x2+.
(2)当x=-时,求y的值.
解:当x=-时,y=2×+=-.
20.某厂仓库储存了部分原料,按原计划每小时消耗2
t,可用60
h.由于技术革新,实际生产能力有所提高,即每小时消耗的原料量大于计划消耗的原料量.设现在每小时消耗原料x(单位:t),库存的原料可使用的时间为y(单位:h).
(1)写出y关于x的函数表达式,并求出自变量的取值范围;
【点拨】由“每小时消耗的原料量×可使用的时间=原料总量”可得y关于x的函数表达式.
解:库存原料为2×60=120(t),根据题意可知y关于x的函数表达式为y=.
由于生产能力提高,每小时消耗的原料量大于计划消耗的原料量,所以自变量的取值范围是x>2.
(2)若恰好经过24
h才有新的原料进厂,为了使机器不停止运转,则x应控制在什么范围内?
【点拨】要使机器不停止运转,需y≥24,解不等式即可.
解:根据题意,得y≥24,
所以≥24.解不等式,得x≤5,
即每小时消耗的原料量应控制在大于2
t且不大于5
t的范围内.
21.如图,正方形ABCD的边长是2,点E,F分别在BC,CD两边上,且点E,F与BC,CD两边的端点不重合,△AEF的面积是1,设BE=x,DF=y.
(1)求y关于x的函数表达式;
解:∵S△ADF+S△ABE+S△CEF=S正方形ABCD-S△AEF=22-1=3,
∴×2y+×2x+(2-x)(2-y)=3,
∴xy=2,
∴y=.
(2)判断在(1)中,y关于x的函数是什么函数?
解:反比例函数.
(3)写出此函数自变量x的范围.
解:1<x<2.
一、选择题
1.下列函数中,y是x的反比例函数的是( )
A.y=
B.y=
C.y=
D.y=+2
2.若函数y=(m+1)x|m|-2是反比例函数,则m=( )
A.±1
B.±3
C.-1
D.1
3.下列各问题中,两个变量之间的关系不是反比例函数的是( )
A.某工程队完成500
m挖渠时,时间t(天)与该工程队挖渠的平均速度v(m/天)之间的关系
B.菱形的面积为36
cm2,它的两条对角线的长y(cm)与x(cm)之间的关系
C.一个玻璃容器的体积为30
L时,所盛液体的质量m与所盛液体的体积V之间的关系
D.压力为600
N时,压强p与受力面积S之间的关系
4.下列函数:①y=;②3xy=1;③y=;④y=.其中反比例函数有( )
A.4个
B.3个
C.2个
D.1个
5.已知y是x的反比例函数,且常数k=,则该函数的表达式是( )
A.y=x
B.y=
C.y=
D.y=
6.【2020·德阳】已知函数y=当函数值为3时,自变量x的值为( )
A.-2
B.-
C.-2或-
D.-2或-
7.【中考·滨州】如图,在平面直角坐标系中,菱形OABC的边OA在x轴的正半轴上,反比例函数y=(x>0)的图象经过对角线OB的中点D和顶点C.若菱形OABC的面积为12,则k的值为( )
A.6
B.5
C.4
D.3
8.下列各组的两个变量间满足反比例关系的是( )
A.三角形面积一定时,它的一边长与该边上的高
B.等腰三角形的周长一定时,它的底边长与腰长
C.圆的周长与它的半径
D.圆的面积与它的半径
9.【中考·广州】一司机驾驶汽车从甲地去乙地,他以平均80千米/时的速度用了4小时到达乙地,当他按原路匀速返回时,汽车的速度v(千米/时)与时间t(小时)的函数关系式是( )
A.v=320t
B.v=
C.v=20t
D.v=
10.【2020·长沙】2019年10月,《长沙晚报》对外发布长沙高铁西站设计方案.该方案以“三湘四水,杜娟花开”为设计理念,塑造出“杜娟花开”的美丽姿态.该高铁站建设初期需要运送大量土石方.某运输公司承担了运送总量为106
m3土石方的任务,该运输公司平均运送土石方的速度v(单位:m3/天)与完成运送任务所需时间t(单位:天)之间的函数表达式是( )
A.v=
B.v=106t C.v=t2 D.v=106t2
二、填空题
11.一般地,如果两个变量y与x的关系可以表示成y=(k为常数,k≠0)的形式,那么称y是x的__________函数,其中x是自变量,常数k(k≠0)称为反比例函数的比例系数.反比例函数的自变量取值范围是___________.反比例函数y=(k≠0)的表达式还可以表示为:①xy=k;②y=kx-1.
12.已知y与x成反比例关系,且当x=-3时,y=4,则当x=6时,y的值为________.
13.如果关于x,y的反比例函数的表达式为y=,那么m的值为________.
14.已知函数y=(a+1)x|2a|-1.
(1)当a=________时,y是x的正比例函数,函数表达式为________;
(2)当a=________时,y是x的反比例函数,函数表达式为________.
三、解答题
15.在下列函数关系式中,哪些函数表示y是x的反比例函数?
(1)y=;(2)y=;(3)y=;(4)xy=;(5)y=;(6)y=-;(7)y=2x-1;(8)y=(a≠5,a是常数).
16.若y=(m+2)xm-5为反比例函数,求反比例函数的表达式.
17.有一个面积为30的梯形,其上底长是下底长的一半,设下底长为x,高为y,求y关于x的函数表达式.这个函数是反比例函数吗?若是,请指出比例系数;若不是,请判断函数类型.
18.李贝说:“在如图所示的矩形ABCD中,AB=6,BC=8,P是BC边上一动点,连接AP,过点D作DE⊥AP于点E.设AP=x(6≤x≤10),DE=y,则y是x的反比例函数.”你认为李贝说得对吗?请给出证明.
19.已知y=y1+y2,y1与x2成正比例函数关系,y2与x成反比例函数关系,且当x=1时,y=3;当x=-1时,y=1.
(1)求y与x之间的函数表达式;
(2)当x=-时,求y的值.
20.某厂仓库储存了部分原料,按原计划每小时消耗2
t,可用60
h.由于技术革新,实际生产能力有所提高,即每小时消耗的原料量大于计划消耗的原料量.设现在每小时消耗原料x(单位:t),库存的原料可使用的时间为y(单位:h).
(1)写出y关于x的函数表达式,并求出自变量的取值范围;
(2)若恰好经过24
h才有新的原料进厂,为了使机器不停止运转,则x应控制在什么范围内?
21.如图,正方形ABCD的边长是2,点E,F分别在BC,CD两边上,且点E,F与BC,CD两边的端点不重合,△AEF的面积是1,设BE=x,DF=y.
(1)求y关于x的函数表达式;
(2)判断在(1)中,y关于x的函数是什么函数?
(3)写出此函数自变量x的范围.
中小学教育资源及组卷应用平台
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.下列函数中,y是x的反比例函数的是( B )
A.y=
B.y=
C.y=
D.y=+2
2.若函数y=(m+1)x|m|-2是反比例函数,则m=( D )
A.±1
B.±3
C.-1
D.1
3.下列各问题中,两个变量之间的关系不是反比例函数的是( C )
A.某工程队完成500
m挖渠时,时间t(天)与该工程队挖渠的平均速度v(m/天)之间的关系
B.菱形的面积为36
cm2,它的两条对角线的长y(cm)与x(cm)之间的关系
C.一个玻璃容器的体积为30
L时,所盛液体的质量m与所盛液体的体积V之间的关系
D.压力为600
N时,压强p与受力面积S之间的关系
4.下列函数:①y=;②3xy=1;③y=;④y=.其中反比例函数有( B )
A.4个
B.3个
C.2个
D.1个
5.已知y是x的反比例函数,且常数k=,则该函数的表达式是( B )
A.y=x
B.y=
C.y=
D.y=
6.【2020·德阳】已知函数y=当函数值为3时,自变量x的值为( A )
A.-2
B.-
C.-2或-
D.-2或-
【解析】若x<2,当y=3时,-x+1=3,
解得x=-2;
若x≥2,当y=3时,-=3,
解得x=-,不合题意,舍去;∴x=-2.
7.【中考·滨州】如图,在平面直角坐标系中,菱形OABC的边OA在x轴的正半轴上,反比例函数y=(x>0)的图象经过对角线OB的中点D和顶点C.若菱形OABC的面积为12,则k的值为( )
A.6
B.5
C.4
D.3
【解析】设点A的坐标为(a,0),点C的坐标为,则点D的坐标为.
∴解得k=4.
8.下列各组的两个变量间满足反比例关系的是( )
A.三角形面积一定时,它的一边长与该边上的高
B.等腰三角形的周长一定时,它的底边长与腰长
C.圆的周长与它的半径
D.圆的面积与它的半径
【解析】A选项中设三角形面积为S,一边长为a,该边上的高为h,则有a=;B选项中设三角形的周长为C,底边长为a,腰长为b,则有a=C-2b;
C选项中设圆的周长为C,半径为r,则有C=2πr;
D选项中设圆的面积为S,半径为r,则有S=πr2.观察可得,只有A选项中的两个变量间满足反比例关系.
9.【中考·广州】一司机驾驶汽车从甲地去乙地,他以平均80千米/时的速度用了4小时到达乙地,当他按原路匀速返回时,汽车的速度v(千米/时)与时间t(小时)的函数关系式是( B )
A.v=320t
B.v=
C.v=20t
D.v=
10.【2020·长沙】2019年10月,《长沙晚报》对外发布长沙高铁西站设计方案.该方案以“三湘四水,杜娟花开”为设计理念,塑造出“杜娟花开”的美丽姿态.该高铁站建设初期需要运送大量土石方.某运输公司承担了运送总量为106
m3土石方的任务,该运输公司平均运送土石方的速度v(单位:m3/天)与完成运送任务所需时间t(单位:天)之间的函数表达式是( A )
A.v=
B.v=106t C.v=t2 D.v=106t2
【点拨】∵运送土石方的总量=平均运送土石方的速度v×完成运送任务所需时间t,
∴106=vt.∴v=.
二、填空题
11.一般地,如果两个变量y与x的关系可以表示成y=(k为常数,k≠0)的形式,那么称y是x的__________函数,其中x是自变量,常数k(k≠0)称为反比例函数的比例系数.反比例函数的自变量取值范围是___________.反比例函数y=(k≠0)的表达式还可以表示为:①xy=k;②y=kx-1.
【答案】反比例;所有非零实数
12.已知y与x成反比例关系,且当x=-3时,y=4,则当x=6时,y的值为________.
【点拨】设反比例函数的表达式为y=(k≠0),
∵当x=-3时,y=4,∴4=,解得k=-12.
∴反比例函数的表达式为y=.
∴当x=6时,y==-2.
13.如果关于x,y的反比例函数的表达式为y=,那么m的值为________.
【点拨】∵反比例函数的表达式为y=,∴
∴|m|=3且m≠-3.∴m=3.
14.已知函数y=(a+1)x|2a|-1.
(1)当a=________时,y是x的正比例函数,函数表达式为________;
(2)当a=________时,y是x的反比例函数,函数表达式为________.
【答案】1
y=2x
0
y=
三、解答题
15.在下列函数关系式中,哪些函数表示y是x的反比例函数?
(1)y=;(2)y=;(3)y=;(4)xy=;(5)y=;(6)y=-;(7)y=2x-1;(8)y=(a≠5,a是常数).
【点拨】根据反比例函数的概念,必须是形如y=(k是常数,且k≠0)的函数,才是反比例函数.如(2),(3),(6),(8)均符合这一概念的要求,所以它们都是反比例函数.但还要注意y=(k是常数,且k≠0)常见的变化形式,如xy=k,y=kx-1等,所以(4),(7)也是反比例函数.对于(5),y是(x-1)的反比例函数,而不是x的反比例函数.(1)中y是x的正比例函数.故(2)(3)(4)(6)(7)(8)是表示y是x的反比例函数.
16.若y=(m+2)xm-5为反比例函数,求反比例函数的表达式.
解:∵y=(m+2)xm-5为反比例函数,
∴m-5=-1且m+2≠0,解得m=4.
∴反比例函数的表达式为y=.
17.有一个面积为30的梯形,其上底长是下底长的一半,设下底长为x,高为y,求y关于x的函数表达式.这个函数是反比例函数吗?若是,请指出比例系数;若不是,请判断函数类型.
解:由题意得y×=30,则y=,故这个函数是反比例函数,比例系数是40.
18.李贝说:“在如图所示的矩形ABCD中,AB=6,BC=8,P是BC边上一动点,连接AP,过点D作DE⊥AP于点E.设AP=x(6≤x≤10),DE=y,则y是x的反比例函数.”你认为李贝说得对吗?请给出证明.
解:李贝说得对.证明如下:
连接DP.
∵四边形ABCD是矩形,
∴AD=BC=8,AB⊥AD,AD∥BC.
∴AB与△ADP的AD边上的高等长.
∴S△ADP=AD·AB=×8×6=24.
又S△ADP=AP·DE=xy,
∴xy=48.
∴y=(6≤x≤10),
即y是x的反比例函数.
19.已知y=y1+y2,y1与x2成正比例函数关系,y2与x成反比例函数关系,且当x=1时,y=3;当x=-1时,y=1.
(1)求y与x之间的函数表达式;
解:设y1=k1x2,y2=(k1≠0,k2≠0),则y=k1x2+.
将x=1,y=3和x=-1,y=1分别代入,
得解得
∴y与x之间的函数表达式为y=2x2+.
(2)当x=-时,求y的值.
解:当x=-时,y=2×+=-.
20.某厂仓库储存了部分原料,按原计划每小时消耗2
t,可用60
h.由于技术革新,实际生产能力有所提高,即每小时消耗的原料量大于计划消耗的原料量.设现在每小时消耗原料x(单位:t),库存的原料可使用的时间为y(单位:h).
(1)写出y关于x的函数表达式,并求出自变量的取值范围;
【点拨】由“每小时消耗的原料量×可使用的时间=原料总量”可得y关于x的函数表达式.
解:库存原料为2×60=120(t),根据题意可知y关于x的函数表达式为y=.
由于生产能力提高,每小时消耗的原料量大于计划消耗的原料量,所以自变量的取值范围是x>2.
(2)若恰好经过24
h才有新的原料进厂,为了使机器不停止运转,则x应控制在什么范围内?
【点拨】要使机器不停止运转,需y≥24,解不等式即可.
解:根据题意,得y≥24,
所以≥24.解不等式,得x≤5,
即每小时消耗的原料量应控制在大于2
t且不大于5
t的范围内.
21.如图,正方形ABCD的边长是2,点E,F分别在BC,CD两边上,且点E,F与BC,CD两边的端点不重合,△AEF的面积是1,设BE=x,DF=y.
(1)求y关于x的函数表达式;
解:∵S△ADF+S△ABE+S△CEF=S正方形ABCD-S△AEF=22-1=3,
∴×2y+×2x+(2-x)(2-y)=3,
∴xy=2,
∴y=.
(2)判断在(1)中,y关于x的函数是什么函数?
解:反比例函数.
(3)写出此函数自变量x的范围.
解:1<x<2.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
