1.2.1 反比例函数y=k/x(k>0)的图象与性质同步练习(含答案)
文档属性
| 名称 | 1.2.1 反比例函数y=k/x(k>0)的图象与性质同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-28 00:00:00 | ||
图片预览




文档简介
1.2 反比例函数的图象与性质
第1课时
反比例函数y=(k>0)的图象与性质
一、选择题
1.反比例函数y=的图象可能是( )
2.若反比例函数y=的图象在第一、三象限,则m的值可能是( )
A.0
B.1
C.2
D.3
3.【中考·柳州】反比例函数y=的图象位于( )
A.第一、三象限
B.第二、三象限
C.第一、二象限
D.第二、四象限
4.已知反比例函数y=的图象与一次函数y=-kx-1的图象在同一坐标系中的大致位置如图所示,则下列结论中正确的是( )
A.k>0,b>0
B.k<0,b<0
C.k>0,b<0
D.k<0,b>0
第4题图
第5题图
第9题图
第10题图
5.如图,点A,B在反比例函数y=(k>0,x>0)的图象上,过点A,B分别作x轴、y轴的垂线,则S1与S2的大小关系是(
)
A.S1>S2
B.S1=S2
C.S1D.无法确定
6.【2020·衡阳】反比例函数y=的图象经过点(2,1),则下列说法错误的是( )
A.k=2
B.函数图象分布在第一、三象限
C.当x>0时,y随x的增大而增大
D.当x>0时,y随x的增大而减小
7.在反比例函数y=的图象的每一支曲线上,y都随x的增大而减小,则k的取值范围是( )
A.k>1
B.k>0
C.k≥1
D.k<1
8.对于反比例函数y=的图象的对称性叙述错误的是( )
A.关于原点中心对称
B.关于直线y=x对称
C.关于直线y=-x对称
D.关于x轴对称
9.反比例函数y=在第一象限的图象如图所示,则k的值可能是( )
A.1
B.2
C.3
D.4
10.如图,函数y=(x>0)、y=(x>0)的图象将第一象限分成了A,B,C三个部分.点Q(a,2)在B部分,则a的取值范围是( )
A.2B.1C.1D.211.【2020·内江】如图,点A是反比例函数y=图象上的一点,过点A作AC⊥x轴,垂足为C,D为AC的中点,若△AOD的面积为1,则k的值为( )
A.
B.
C.3
D.4
12.反比例函数y=图象上三个点的坐标为(x1,y1),(x2,y2),(x3,y3),若x1<x2<0<x3,则y1,y2,y3的大小关系是( )
A.y1<y2<y3
B.y2<y1<y3
C.y2<y3<y1
D.y1<y3<y2
二、填空题
13.一般地,当k>0时,反比例函数y=的图象由分别在第________、________象限内的两支曲线组成,它们与x轴、y轴都不相交,在每个象限内,函数值y随自变量x的增大而________.
14.在函数y=(a为常数)的图象上有三个点(-1,y1),,,则函数值y1,y2,y3的大小关系是________________.
15.【2020·北京】在平面直角坐标系xOy中,直线y=x与双曲线y=(m≠0)交于A,B两点.若点A,B的纵坐标分别为y1,y2,则y1+y2的值为________.
16.已知P1(x1,y1),P2(x2,y2)两点都在反比例函数y=的图象上,且x1 y2.(填“>”或“<”)?
17.如图,点A,B分别在反比例函数y=和y=的图象上,且AB∥x轴,则△OAB的面积等于?
.?
第17题图
第18题图
第19题图
18.如图,已知点P(6,3),过点P作PM⊥x轴于点M,PN⊥y轴于点N,反比例函数y=的图象交PM于点A,交PN于点B.若四边形OAPB的面积为12,则k=
.
19.【兰州中考】如图,点P,Q是反比例函数y=图象上的两点,PA⊥y轴于点A,QN⊥x轴于点N,作PM⊥x轴于点M,QB⊥y轴于点B,连接PB,QM,记△ABP的面积为S1,△QMN的面积为S2,则S1
S2(选填“>”“<”或“=”).
三、解答题
20.通过课本上对函数的学习,我们积累了一定的经验,下表是一个函数的自变量x与函数值y的部分对应值,请你借鉴以往学习函数的经验,探究下列问题:
x
…
1
2
3
4
5
6
…
y
…
6
3
2
1.5
1.2
1
…
(1)当x=________时,y=1.5;
(2)根据表中数值在下面的坐标系中描点,并画出函数图象;
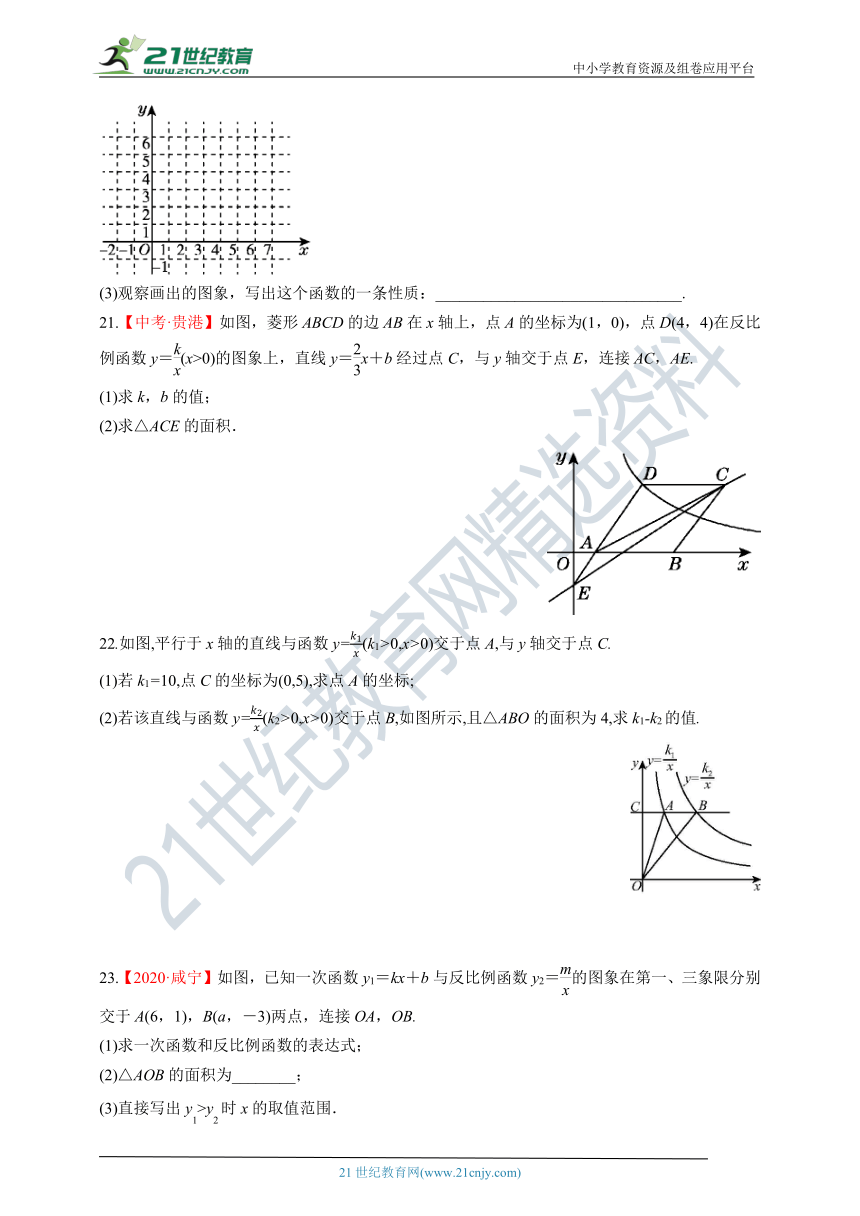
(3)观察画出的图象,写出这个函数的一条性质:_______________________________.
21.【中考·贵港】如图,菱形ABCD的边AB在x轴上,点A的坐标为(1,0),点D(4,4)在反比例函数y=(x>0)的图象上,直线y=x+b经过点C,与y轴交于点E,连接AC,AE.
(1)求k,b的值;
(2)求△ACE的面积.
22.如图,平行于x轴的直线与函数y=(k1>0,x>0)交于点A,与y轴交于点C.
(1)若k1=10,点C的坐标为(0,5),求点A的坐标;
(2)若该直线与函数y=(k2>0,x>0)交于点B,如图所示,且△ABO的面积为4,求k1-k2的值.
23.【2020·咸宁】如图,已知一次函数y1=kx+b与反比例函数y2=的图象在第一、三象限分别交于A(6,1),B(a,-3)两点,连接OA,OB.
(1)求一次函数和反比例函数的表达式;
(2)△AOB的面积为________;
(3)直接写出y1>y2时x的取值范围.
24.【中考·苏州】如图,在△ABC中,AC=BC,AB⊥x轴,垂足为A.反比例函数y=(x>0)的图象经过点C,交AB于点D.已知AB=4,BC=.
(1)若OA=4,求k的值;
(2)连接OC,若BD=BC,求OC的长.
25.如图,在平面直角坐标系中,矩形ABCD的顶点B,C在x轴的正半轴上,AB=8,BC=6.对角线AC,BD相交于点E,反比例函数y=(x>0)的图象经过点E,分别与AB,CD交于点F,G.
(1)若OC=8,求k的值;
(2)连接EG,若BF-BE=2,求△CEG的面积.
中小学教育资源及组卷应用平台
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.反比例函数y=的图象可能是( D )
2.若反比例函数y=的图象在第一、三象限,则m的值可能是( A )
A.0
B.1
C.2
D.3
3.【中考·柳州】反比例函数y=的图象位于( A )
A.第一、三象限
B.第二、三象限
C.第一、二象限
D.第二、四象限
【点拨】∵k=2>0,∴反比例函数的图象位于第一、三象限.
4.已知反比例函数y=的图象与一次函数y=-kx-1的图象在同一坐标系中的大致位置如图所示,则下列结论中正确的是( B )
A.k>0,b>0
B.k<0,b<0
C.k>0,b<0
D.k<0,b>0
第4题图
第5题图
第9题图
第10题图
5.如图,点A,B在反比例函数y=(k>0,x>0)的图象上,过点A,B分别作x轴、y轴的垂线,则S1与S2的大小关系是(B)
A.S1>S2
B.S1=S2
C.S1D.无法确定
6.【2020·衡阳】反比例函数y=的图象经过点(2,1),则下列说法错误的是( C )
A.k=2
B.函数图象分布在第一、三象限
C.当x>0时,y随x的增大而增大
D.当x>0时,y随x的增大而减小
7.在反比例函数y=的图象的每一支曲线上,y都随x的增大而减小,则k的取值范围是( A )
A.k>1
B.k>0
C.k≥1
D.k<1
8.对于反比例函数y=的图象的对称性叙述错误的是( )
A.关于原点中心对称
B.关于直线y=x对称
C.关于直线y=-x对称
D.关于x轴对称
【点拨】反比例函数y=的图象关于原点中心对称、关于直线y=x对称、关于直线y=-x对称,∵它的图象在第一、三象限,∴不关于x轴对称,A,B,C说法正确,不符合题意,D说法错误,符合题意,故选D.
9.反比例函数y=在第一象限的图象如图所示,则k的值可能是( C )
A.1
B.2
C.3
D.4
10.如图,函数y=(x>0)、y=(x>0)的图象将第一象限分成了A,B,C三个部分.点Q(a,2)在B部分,则a的取值范围是( )
A.2B.1C.1D.2【点拨】过点(0,
2)作x轴的平行线,分别与y=(x>0)、y=(x>0)的图象交于点M,N,易得M(1,2),N(3,2),所以点Q(a,2)落在线段MN上,∴1<a<3.本题易错点:忽略点Q的位置,而只从函数的比例系数上判定得出2<a<6的错误结论.
【答案】B
11.【2020·内江】如图,点A是反比例函数y=图象上的一点,过点A作AC⊥x轴,垂足为C,D为AC的中点,若△AOD的面积为1,则k的值为( D )
A.
B.
C.3
D.4
12.反比例函数y=图象上三个点的坐标为(x1,y1),(x2,y2),(x3,y3),若x1<x2<0<x3,则y1,y2,y3的大小关系是( )
A.y1<y2<y3
B.y2<y1<y3
C.y2<y3<y1
D.y1<y3<y2
【点拨】∵反比例函数y=中,k=3>0,
∴此函数图象的两个分支分别位于第一、三象限,且在每一个象限内y随x的增大而减小.
∵x1<x2<0<x3,
∴点(x1,y1),(x2,y2)在第三象限,点(x3,y3)在第一象限.∴y2<y1<0<y3.
二、填空题
13.一般地,当k>0时,反比例函数y=的图象由分别在第________、________象限内的两支曲线组成,它们与x轴、y轴都不相交,在每个象限内,函数值y随自变量x的增大而________.
【答案】一;三;减小
14.在函数y=(a为常数)的图象上有三个点(-1,y1),,,则函数值y1,y2,y3的大小关系是________________.
【点拨】∵反比例函数的比例系数a2+1>0,∴图象的两个分支在第一、三象限,且在每个象限内,y随x的增大而减小,
∵-1<-<0,∴点(-1,y1),在第三象限,
∴y2<y1<0,∵>0,∴点在第一象限,
∴y3>0,∴y2<y1<y3.
【答案】y2<y1<y3
15.【2020·北京】在平面直角坐标系xOy中,直线y=x与双曲线y=(m≠0)交于A,B两点.若点A,B的纵坐标分别为y1,y2,则y1+y2的值为________.
【答案】0
16.已知P1(x1,y1),P2(x2,y2)两点都在反比例函数y=的图象上,且x1 y2.(填“>”或“<”)?
【答案】 >
17.如图,点A,B分别在反比例函数y=和y=的图象上,且AB∥x轴,则△OAB的面积等于?
.?
【答案】?
第17题图
第18题图
第19题图
18.如图,已知点P(6,3),过点P作PM⊥x轴于点M,PN⊥y轴于点N,反比例函数y=的图象交PM于点A,交PN于点B.若四边形OAPB的面积为12,则k=
.
【答案】
6
19.【兰州中考】如图,点P,Q是反比例函数y=图象上的两点,PA⊥y轴于点A,QN⊥x轴于点N,作PM⊥x轴于点M,QB⊥y轴于点B,连接PB,QM,记△ABP的面积为S1,△QMN的面积为S2,则S1
S2(选填“>”“<”或“=”).
【答案】=
三、解答题
20.通过课本上对函数的学习,我们积累了一定的经验,下表是一个函数的自变量x与函数值y的部分对应值,请你借鉴以往学习函数的经验,探究下列问题:
x
…
1
2
3
4
5
6
…
y
…
6
3
2
1.5
1.2
1
…
(1)当x=________时,y=1.5;
【答案】
4
(2)根据表中数值在下面的坐标系中描点,并画出函数图象;
解:略.
(3)观察画出的图象,写出这个函数的一条性质:
_______________________________.
(答案不唯一)图象与x轴没有交点
21.【中考·贵港】如图,菱形ABCD的边AB在x轴上,点A的坐标为(1,0),点D(4,4)在反比例函数y=(x>0)的图象上,直线y=x+b经过点C,与y轴交于点E,连接AC,AE.
(1)求k,b的值;
解:由已知易得AD=5,
∵四边形ABCD是菱形,
∴B(6,0),C(9,4).
将点C(9,4)的坐标代入y=x+b,得b=-2.
∵点D(4,4)在反比例函数y=(x>0)的图象上,
∴k=16.
(2)求△ACE的面积.
解:由(1)易得点E的坐标为(0,-2),
直线y=x-2与x轴的交点坐标为(3,0),
∴S△AEC=×(3-1)×(2+4)=6.
22.如图,平行于x轴的直线与函数y=(k1>0,x>0)交于点A,与y轴交于点C.
(1)若k1=10,点C的坐标为(0,5),求点A的坐标;
(2)若该直线与函数y=(k2>0,x>0)交于点B,如图所示,且△ABO的面积为4,求k1-k2的值.
21.解:(1)设点A的坐标为(a,b),
∵AC∥x轴,点C的坐标为(0,5),∴b=5.
又∵点A在反比例函数y=的图象上,∴5a=10,∴a=2,∴点A的坐标为(2,5).
(2)由反比例函数中k的几何意义可得k1,k2.
∵,∴4=(k2-k1),
∴k2-k1=8,即k1-k2=-8.
23.【2020·咸宁】如图,已知一次函数y1=kx+b与反比例函数y2=的图象在第一、三象限分别交于A(6,1),B(a,-3)两点,连接OA,OB.
(1)求一次函数和反比例函数的表达式;
解:把点A(6,1)的坐标代入y2=中,解得m=6.故反比例函数的表达式为y2=.
把点B(a,-3)的坐标代入y2=中,解得a=-2.故B(-2,-3).
把点A(6,1),B(-2,-3)的坐标分别代入y1=kx+b中,得解得
故一次函数的表达式为y1=x-2.
(2)△AOB的面积为________;
【答案】
8
(3)直接写出y1>y2时x的取值范围.
解:y1>y2时x的取值范围是-2<x<0或x>6.
24.【中考·苏州】如图,在△ABC中,AC=BC,AB⊥x轴,垂足为A.反比例函数y=(x>0)的图象经过点C,交AB于点D.已知AB=4,BC=.
(1)若OA=4,求k的值;
解:如图,过点C作CE⊥AB,垂足为E.
∵AC=BC,AB=4,∴AE=BE=2.
在Rt△BCE中,BC=,BE=2,∴CE=.
∵OA=4,∴OF=.∴点C的坐标为.
∵点C在反比例函数y=的图象上,∴k=5.
(2)连接OC,若BD=BC,求OC的长.
解:如图,设点A的坐标为(m,0),
∵AB=4,BD=BC=,∴AD=,
∴D,C两点的坐标分别为,.
∵点C,D都在反比例函数y=的图象上,
∴m=2.∴m=6.∴点C的坐标为.
过点C作CF⊥x轴,垂足为F,∴OF=,CF=2,
在Rt△OFC中,OC2=OF2+CF2,∴OC=.
25.如图,在平面直角坐标系中,矩形ABCD的顶点B,C在x轴的正半轴上,AB=8,BC=6.对角线AC,BD相交于点E,反比例函数y=(x>0)的图象经过点E,分别与AB,CD交于点F,G.
(1)若OC=8,求k的值;
解:∵在矩形ABCD中,AB=8,BC=6,而OC=8,
∴B(2,0),A(2,8),C(8,0).
∵对角线AC,BD相交于点E,
∴点E为AC的中点,
∴E(5,4),把(5,4)代入y=得k=5×4=20.
(2)连接EG,若BF-BE=2,求△CEG的面积.
解:∵AC==10,∴BE=EC=5,
∵BF-BE=2,∴BF=7,
设OB=t,则F(t,7),E(t+3,4).
∵反比例函数y=(x>0)的图象经过点E、F,
∴7t=4(t+3),解得t=4,∴k=7t=28,
∴反比例函数的表达式为y=,
当x=4+6=10时,y==,
∴G,
∴△CEG的面积=×3×=.
中小学教育资源及组卷应用平台
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
第1课时
反比例函数y=(k>0)的图象与性质
一、选择题
1.反比例函数y=的图象可能是( )
2.若反比例函数y=的图象在第一、三象限,则m的值可能是( )
A.0
B.1
C.2
D.3
3.【中考·柳州】反比例函数y=的图象位于( )
A.第一、三象限
B.第二、三象限
C.第一、二象限
D.第二、四象限
4.已知反比例函数y=的图象与一次函数y=-kx-1的图象在同一坐标系中的大致位置如图所示,则下列结论中正确的是( )
A.k>0,b>0
B.k<0,b<0
C.k>0,b<0
D.k<0,b>0
第4题图
第5题图
第9题图
第10题图
5.如图,点A,B在反比例函数y=(k>0,x>0)的图象上,过点A,B分别作x轴、y轴的垂线,则S1与S2的大小关系是(
)
A.S1>S2
B.S1=S2
C.S1
6.【2020·衡阳】反比例函数y=的图象经过点(2,1),则下列说法错误的是( )
A.k=2
B.函数图象分布在第一、三象限
C.当x>0时,y随x的增大而增大
D.当x>0时,y随x的增大而减小
7.在反比例函数y=的图象的每一支曲线上,y都随x的增大而减小,则k的取值范围是( )
A.k>1
B.k>0
C.k≥1
D.k<1
8.对于反比例函数y=的图象的对称性叙述错误的是( )
A.关于原点中心对称
B.关于直线y=x对称
C.关于直线y=-x对称
D.关于x轴对称
9.反比例函数y=在第一象限的图象如图所示,则k的值可能是( )
A.1
B.2
C.3
D.4
10.如图,函数y=(x>0)、y=(x>0)的图象将第一象限分成了A,B,C三个部分.点Q(a,2)在B部分,则a的取值范围是( )
A.2
A.
B.
C.3
D.4
12.反比例函数y=图象上三个点的坐标为(x1,y1),(x2,y2),(x3,y3),若x1<x2<0<x3,则y1,y2,y3的大小关系是( )
A.y1<y2<y3
B.y2<y1<y3
C.y2<y3<y1
D.y1<y3<y2
二、填空题
13.一般地,当k>0时,反比例函数y=的图象由分别在第________、________象限内的两支曲线组成,它们与x轴、y轴都不相交,在每个象限内,函数值y随自变量x的增大而________.
14.在函数y=(a为常数)的图象上有三个点(-1,y1),,,则函数值y1,y2,y3的大小关系是________________.
15.【2020·北京】在平面直角坐标系xOy中,直线y=x与双曲线y=(m≠0)交于A,B两点.若点A,B的纵坐标分别为y1,y2,则y1+y2的值为________.
16.已知P1(x1,y1),P2(x2,y2)两点都在反比例函数y=的图象上,且x1
17.如图,点A,B分别在反比例函数y=和y=的图象上,且AB∥x轴,则△OAB的面积等于?
.?
第17题图
第18题图
第19题图
18.如图,已知点P(6,3),过点P作PM⊥x轴于点M,PN⊥y轴于点N,反比例函数y=的图象交PM于点A,交PN于点B.若四边形OAPB的面积为12,则k=
.
19.【兰州中考】如图,点P,Q是反比例函数y=图象上的两点,PA⊥y轴于点A,QN⊥x轴于点N,作PM⊥x轴于点M,QB⊥y轴于点B,连接PB,QM,记△ABP的面积为S1,△QMN的面积为S2,则S1
S2(选填“>”“<”或“=”).
三、解答题
20.通过课本上对函数的学习,我们积累了一定的经验,下表是一个函数的自变量x与函数值y的部分对应值,请你借鉴以往学习函数的经验,探究下列问题:
x
…
1
2
3
4
5
6
…
y
…
6
3
2
1.5
1.2
1
…
(1)当x=________时,y=1.5;
(2)根据表中数值在下面的坐标系中描点,并画出函数图象;
(3)观察画出的图象,写出这个函数的一条性质:_______________________________.
21.【中考·贵港】如图,菱形ABCD的边AB在x轴上,点A的坐标为(1,0),点D(4,4)在反比例函数y=(x>0)的图象上,直线y=x+b经过点C,与y轴交于点E,连接AC,AE.
(1)求k,b的值;
(2)求△ACE的面积.
22.如图,平行于x轴的直线与函数y=(k1>0,x>0)交于点A,与y轴交于点C.
(1)若k1=10,点C的坐标为(0,5),求点A的坐标;
(2)若该直线与函数y=(k2>0,x>0)交于点B,如图所示,且△ABO的面积为4,求k1-k2的值.
23.【2020·咸宁】如图,已知一次函数y1=kx+b与反比例函数y2=的图象在第一、三象限分别交于A(6,1),B(a,-3)两点,连接OA,OB.
(1)求一次函数和反比例函数的表达式;
(2)△AOB的面积为________;
(3)直接写出y1>y2时x的取值范围.
24.【中考·苏州】如图,在△ABC中,AC=BC,AB⊥x轴,垂足为A.反比例函数y=(x>0)的图象经过点C,交AB于点D.已知AB=4,BC=.
(1)若OA=4,求k的值;
(2)连接OC,若BD=BC,求OC的长.
25.如图,在平面直角坐标系中,矩形ABCD的顶点B,C在x轴的正半轴上,AB=8,BC=6.对角线AC,BD相交于点E,反比例函数y=(x>0)的图象经过点E,分别与AB,CD交于点F,G.
(1)若OC=8,求k的值;
(2)连接EG,若BF-BE=2,求△CEG的面积.
中小学教育资源及组卷应用平台
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.反比例函数y=的图象可能是( D )
2.若反比例函数y=的图象在第一、三象限,则m的值可能是( A )
A.0
B.1
C.2
D.3
3.【中考·柳州】反比例函数y=的图象位于( A )
A.第一、三象限
B.第二、三象限
C.第一、二象限
D.第二、四象限
【点拨】∵k=2>0,∴反比例函数的图象位于第一、三象限.
4.已知反比例函数y=的图象与一次函数y=-kx-1的图象在同一坐标系中的大致位置如图所示,则下列结论中正确的是( B )
A.k>0,b>0
B.k<0,b<0
C.k>0,b<0
D.k<0,b>0
第4题图
第5题图
第9题图
第10题图
5.如图,点A,B在反比例函数y=(k>0,x>0)的图象上,过点A,B分别作x轴、y轴的垂线,则S1与S2的大小关系是(B)
A.S1>S2
B.S1=S2
C.S1
6.【2020·衡阳】反比例函数y=的图象经过点(2,1),则下列说法错误的是( C )
A.k=2
B.函数图象分布在第一、三象限
C.当x>0时,y随x的增大而增大
D.当x>0时,y随x的增大而减小
7.在反比例函数y=的图象的每一支曲线上,y都随x的增大而减小,则k的取值范围是( A )
A.k>1
B.k>0
C.k≥1
D.k<1
8.对于反比例函数y=的图象的对称性叙述错误的是( )
A.关于原点中心对称
B.关于直线y=x对称
C.关于直线y=-x对称
D.关于x轴对称
【点拨】反比例函数y=的图象关于原点中心对称、关于直线y=x对称、关于直线y=-x对称,∵它的图象在第一、三象限,∴不关于x轴对称,A,B,C说法正确,不符合题意,D说法错误,符合题意,故选D.
9.反比例函数y=在第一象限的图象如图所示,则k的值可能是( C )
A.1
B.2
C.3
D.4
10.如图,函数y=(x>0)、y=(x>0)的图象将第一象限分成了A,B,C三个部分.点Q(a,2)在B部分,则a的取值范围是( )
A.2
2)作x轴的平行线,分别与y=(x>0)、y=(x>0)的图象交于点M,N,易得M(1,2),N(3,2),所以点Q(a,2)落在线段MN上,∴1<a<3.本题易错点:忽略点Q的位置,而只从函数的比例系数上判定得出2<a<6的错误结论.
【答案】B
11.【2020·内江】如图,点A是反比例函数y=图象上的一点,过点A作AC⊥x轴,垂足为C,D为AC的中点,若△AOD的面积为1,则k的值为( D )
A.
B.
C.3
D.4
12.反比例函数y=图象上三个点的坐标为(x1,y1),(x2,y2),(x3,y3),若x1<x2<0<x3,则y1,y2,y3的大小关系是( )
A.y1<y2<y3
B.y2<y1<y3
C.y2<y3<y1
D.y1<y3<y2
【点拨】∵反比例函数y=中,k=3>0,
∴此函数图象的两个分支分别位于第一、三象限,且在每一个象限内y随x的增大而减小.
∵x1<x2<0<x3,
∴点(x1,y1),(x2,y2)在第三象限,点(x3,y3)在第一象限.∴y2<y1<0<y3.
二、填空题
13.一般地,当k>0时,反比例函数y=的图象由分别在第________、________象限内的两支曲线组成,它们与x轴、y轴都不相交,在每个象限内,函数值y随自变量x的增大而________.
【答案】一;三;减小
14.在函数y=(a为常数)的图象上有三个点(-1,y1),,,则函数值y1,y2,y3的大小关系是________________.
【点拨】∵反比例函数的比例系数a2+1>0,∴图象的两个分支在第一、三象限,且在每个象限内,y随x的增大而减小,
∵-1<-<0,∴点(-1,y1),在第三象限,
∴y2<y1<0,∵>0,∴点在第一象限,
∴y3>0,∴y2<y1<y3.
【答案】y2<y1<y3
15.【2020·北京】在平面直角坐标系xOy中,直线y=x与双曲线y=(m≠0)交于A,B两点.若点A,B的纵坐标分别为y1,y2,则y1+y2的值为________.
【答案】0
16.已知P1(x1,y1),P2(x2,y2)两点都在反比例函数y=的图象上,且x1
【答案】 >
17.如图,点A,B分别在反比例函数y=和y=的图象上,且AB∥x轴,则△OAB的面积等于?
.?
【答案】?
第17题图
第18题图
第19题图
18.如图,已知点P(6,3),过点P作PM⊥x轴于点M,PN⊥y轴于点N,反比例函数y=的图象交PM于点A,交PN于点B.若四边形OAPB的面积为12,则k=
.
【答案】
6
19.【兰州中考】如图,点P,Q是反比例函数y=图象上的两点,PA⊥y轴于点A,QN⊥x轴于点N,作PM⊥x轴于点M,QB⊥y轴于点B,连接PB,QM,记△ABP的面积为S1,△QMN的面积为S2,则S1
S2(选填“>”“<”或“=”).
【答案】=
三、解答题
20.通过课本上对函数的学习,我们积累了一定的经验,下表是一个函数的自变量x与函数值y的部分对应值,请你借鉴以往学习函数的经验,探究下列问题:
x
…
1
2
3
4
5
6
…
y
…
6
3
2
1.5
1.2
1
…
(1)当x=________时,y=1.5;
【答案】
4
(2)根据表中数值在下面的坐标系中描点,并画出函数图象;
解:略.
(3)观察画出的图象,写出这个函数的一条性质:
_______________________________.
(答案不唯一)图象与x轴没有交点
21.【中考·贵港】如图,菱形ABCD的边AB在x轴上,点A的坐标为(1,0),点D(4,4)在反比例函数y=(x>0)的图象上,直线y=x+b经过点C,与y轴交于点E,连接AC,AE.
(1)求k,b的值;
解:由已知易得AD=5,
∵四边形ABCD是菱形,
∴B(6,0),C(9,4).
将点C(9,4)的坐标代入y=x+b,得b=-2.
∵点D(4,4)在反比例函数y=(x>0)的图象上,
∴k=16.
(2)求△ACE的面积.
解:由(1)易得点E的坐标为(0,-2),
直线y=x-2与x轴的交点坐标为(3,0),
∴S△AEC=×(3-1)×(2+4)=6.
22.如图,平行于x轴的直线与函数y=(k1>0,x>0)交于点A,与y轴交于点C.
(1)若k1=10,点C的坐标为(0,5),求点A的坐标;
(2)若该直线与函数y=(k2>0,x>0)交于点B,如图所示,且△ABO的面积为4,求k1-k2的值.
21.解:(1)设点A的坐标为(a,b),
∵AC∥x轴,点C的坐标为(0,5),∴b=5.
又∵点A在反比例函数y=的图象上,∴5a=10,∴a=2,∴点A的坐标为(2,5).
(2)由反比例函数中k的几何意义可得k1,k2.
∵,∴4=(k2-k1),
∴k2-k1=8,即k1-k2=-8.
23.【2020·咸宁】如图,已知一次函数y1=kx+b与反比例函数y2=的图象在第一、三象限分别交于A(6,1),B(a,-3)两点,连接OA,OB.
(1)求一次函数和反比例函数的表达式;
解:把点A(6,1)的坐标代入y2=中,解得m=6.故反比例函数的表达式为y2=.
把点B(a,-3)的坐标代入y2=中,解得a=-2.故B(-2,-3).
把点A(6,1),B(-2,-3)的坐标分别代入y1=kx+b中,得解得
故一次函数的表达式为y1=x-2.
(2)△AOB的面积为________;
【答案】
8
(3)直接写出y1>y2时x的取值范围.
解:y1>y2时x的取值范围是-2<x<0或x>6.
24.【中考·苏州】如图,在△ABC中,AC=BC,AB⊥x轴,垂足为A.反比例函数y=(x>0)的图象经过点C,交AB于点D.已知AB=4,BC=.
(1)若OA=4,求k的值;
解:如图,过点C作CE⊥AB,垂足为E.
∵AC=BC,AB=4,∴AE=BE=2.
在Rt△BCE中,BC=,BE=2,∴CE=.
∵OA=4,∴OF=.∴点C的坐标为.
∵点C在反比例函数y=的图象上,∴k=5.
(2)连接OC,若BD=BC,求OC的长.
解:如图,设点A的坐标为(m,0),
∵AB=4,BD=BC=,∴AD=,
∴D,C两点的坐标分别为,.
∵点C,D都在反比例函数y=的图象上,
∴m=2.∴m=6.∴点C的坐标为.
过点C作CF⊥x轴,垂足为F,∴OF=,CF=2,
在Rt△OFC中,OC2=OF2+CF2,∴OC=.
25.如图,在平面直角坐标系中,矩形ABCD的顶点B,C在x轴的正半轴上,AB=8,BC=6.对角线AC,BD相交于点E,反比例函数y=(x>0)的图象经过点E,分别与AB,CD交于点F,G.
(1)若OC=8,求k的值;
解:∵在矩形ABCD中,AB=8,BC=6,而OC=8,
∴B(2,0),A(2,8),C(8,0).
∵对角线AC,BD相交于点E,
∴点E为AC的中点,
∴E(5,4),把(5,4)代入y=得k=5×4=20.
(2)连接EG,若BF-BE=2,求△CEG的面积.
解:∵AC==10,∴BE=EC=5,
∵BF-BE=2,∴BF=7,
设OB=t,则F(t,7),E(t+3,4).
∵反比例函数y=(x>0)的图象经过点E、F,
∴7t=4(t+3),解得t=4,∴k=7t=28,
∴反比例函数的表达式为y=,
当x=4+6=10时,y==,
∴G,
∴△CEG的面积=×3×=.
中小学教育资源及组卷应用平台
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
