1.2.3 反比例函数的图象与性质的综合应用同步练习(含答案)
文档属性
| 名称 | 1.2.3 反比例函数的图象与性质的综合应用同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-28 00:00:00 | ||
图片预览


文档简介
1.2 反比例函数的图象与性质
第3课时
反比例函数的图象与性质的综合应用
一、选择题
1.【2019·哈尔滨】点(-1,4)在反比例函数y=的图象上,则下列各点在此函数图象上的是( )
A.(4,-1)
B.
C.(-4,-1)
D.
2.【2021·江苏宿迁】已知双曲线过点(3,)、(1,)、(-2,),则下列结论正确的是(
)
A.
B.
C.
D.
3.如图,正方形ABOC的边长为2,反比例函数y=的图象经过点A,则k的值是
( )
A.2
B.-2
C.4
D.-4
第3题图
第4题图
第6题图
第7题图
4.【2020·怀化】在同一平面直角坐标系中,一次函数y1=k1x+b与反比例函数y2=(x>0)的图象如图所示,则当y1>y2时,自变量x的取值范围为( )
A.x<1
B.x>3
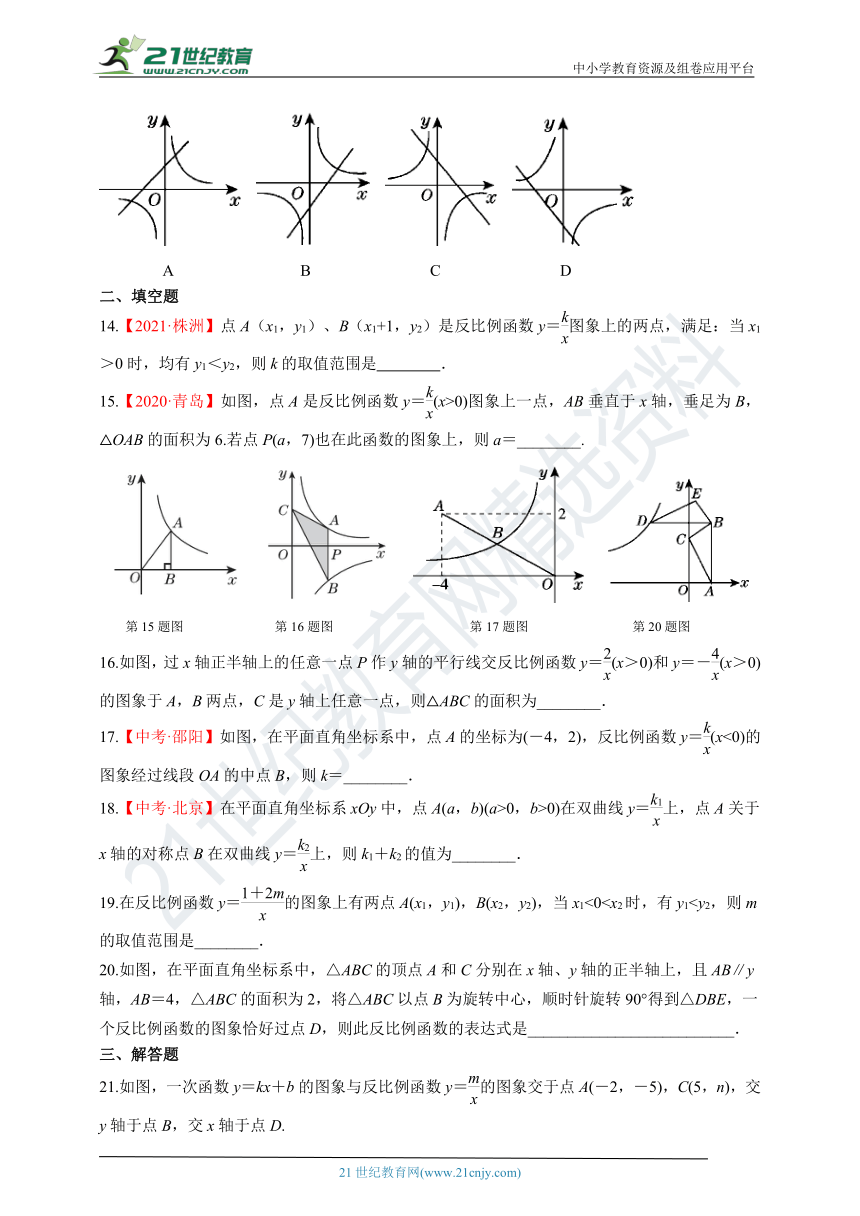
C.0D.15.【2020·新疆改编】一次函数y=mx-1和反比例函数y=在同一平面直角坐标系中的图象可能是( )
6.【中考·湖州】如图,已知直线y=k1x(k1≠0)与反比例函数y=(k2≠0)的图象交于M,N两点.若点M的坐标是(1,2),则点N的坐标是( )
A.(-1,-2)
B.(-1,2)
C.(1,-2)
D.(-2,-1)
7.如图,正方形ABCD的两个顶点B,D在反比例函数y=的图象上,对角线AC,BD的交点恰好是坐标原点O,已知B(-1,1),则k的值是( )
A.-5
B.-4
C.-3
D.-1
8.【2019·株洲】如图,在平面直角坐标系xOy中,点A,B,C为反比例函数y=(k>0)图象上不同的三点,连接OA,OB,OC,过点A作AD⊥y轴于点D,过点B,C分别作BE,CF垂直于x轴于点E,F,OC与BE相交于点M,记△AOD,△BOM,四边形CMEF的面积分别为,,,则( )
A.=+S3
B.=S3
C.>>
D.<
第8题图
第9题图
第11题图
第12题图
4.反比例函数y=的图象经过点M(-6,-2),则反比例函数的表达式为( )
A.y=-
B.y=
C.y=-
D.y=
9.如图,在平面直角坐标系中,过x轴正半轴上任意一点P作y轴的平行线,分别交函数y=(x>0),y=-(x>0)的图象于点A,点B.若C是y轴上任意一点,则△ABC的面积为
( )
A.9
B.6
C.
D.3
10.若点A(3,-2)关于y轴对称的点为B,则图象经过点B的反比例函数的表达式为( )
A.y=6x
B.y=-
C.y=-6x
D.y=
11.如图,正方形ABCD的两个顶点B,D在反比例函数y=的图象上,对角线AC,BD的交点恰好是坐标原点O,已知B(-1,1),则k的值是( )
A.-5
B.-4
C.-3
D.-1
12.【2020·张家界】如图所示,过y轴正半轴上的任意一点P作x轴的平行线,分别与反比例函数y=-和y=的图象交于点A和点B,若点C是x轴上任意一点,连接AC,BC,则△ABC的面积为( )
A.6
B.7
C.8
D.14
13.【中考·通辽】关于x,y的二元一次方程组的解满足xA
B
C
D
二、填空题
14.【2021·株洲】点A(x1,y1)、B(x1+1,y2)是反比例函数y=图象上的两点,满足:当x1>0时,均有y1<y2,则k的取值范围是
.
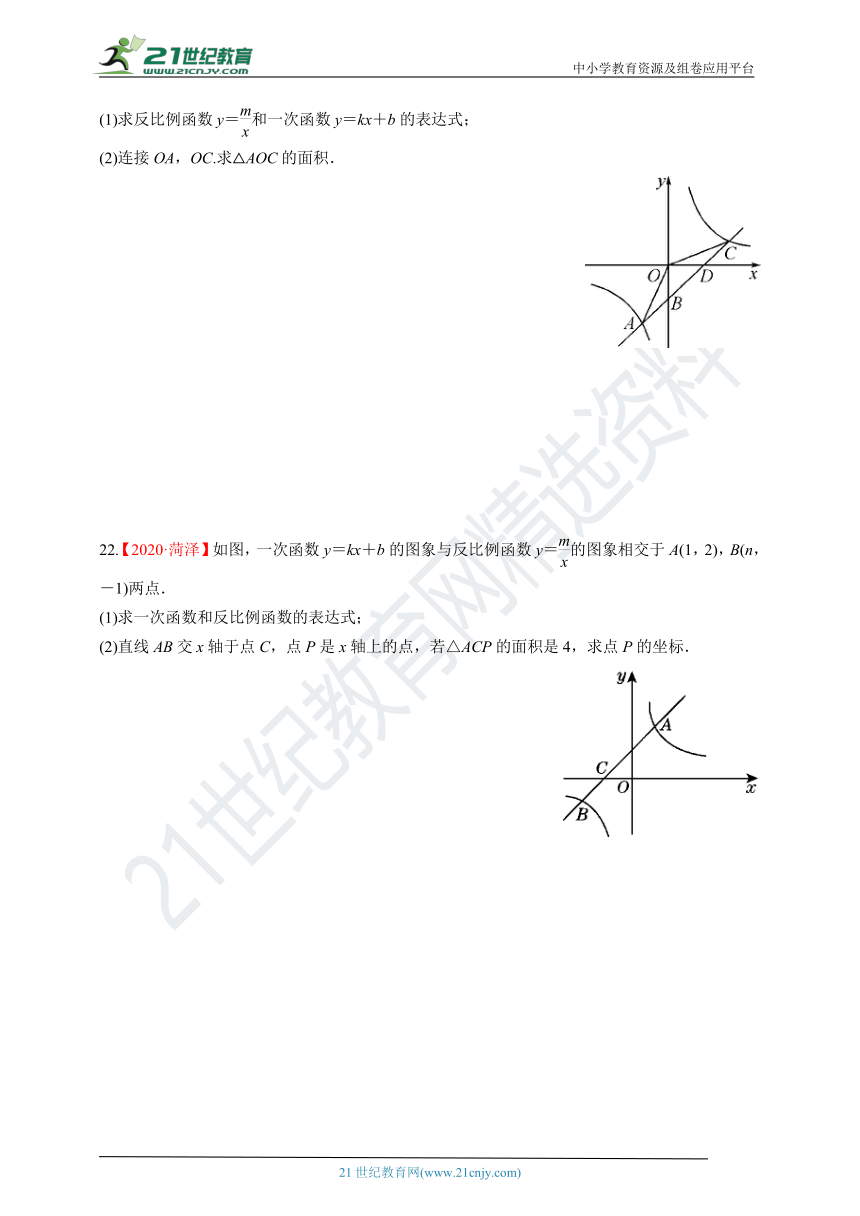
15.【2020·青岛】如图,点A是反比例函数y=(x>0)图象上一点,AB垂直于x轴,垂足为B,△OAB的面积为6.若点P(a,7)也在此函数的图象上,则a=________.
第15题图
第16题图
第17题图
第20题图
16.如图,过x轴正半轴上的任意一点P作y轴的平行线交反比例函数y=(x>0)和y=-(x>0)的图象于A,B两点,C是y轴上任意一点,则△ABC的面积为________.
17.【中考·邵阳】如图,在平面直角坐标系中,点A的坐标为(-4,2),反比例函数y=(x<0)的图象经过线段OA的中点B,则k=________.
18.【中考·北京】在平面直角坐标系xOy中,点A(a,b)(a>0,b>0)在双曲线y=上,点A关于x轴的对称点B在双曲线y=上,则k1+k2的值为________.
19.在反比例函数y=的图象上有两点A(x1,y1),B(x2,y2),当x1<020.如图,在平面直角坐标系中,△ABC的顶点A和C分别在x轴、y轴的正半轴上,且AB∥y轴,AB=4,△ABC的面积为2,将△ABC以点B为旋转中心,顺时针旋转90°得到△DBE,一个反比例函数的图象恰好过点D,则此反比例函数的表达式是__________________________.
三、解答题
21.如图,一次函数y=kx+b的图象与反比例函数y=的图象交于点A(-2,-5),C(5,n),交y轴于点B,交x轴于点D.
(1)求反比例函数y=和一次函数y=kx+b的表达式;
(2)连接OA,OC.求△AOC的面积.
22.【2020·菏泽】如图,一次函数y=kx+b的图象与反比例函数y=的图象相交于A(1,2),B(n,-1)两点.
(1)求一次函数和反比例函数的表达式;
(2)直线AB交x轴于点C,点P是x轴上的点,若△ACP的面积是4,求点P的坐标.
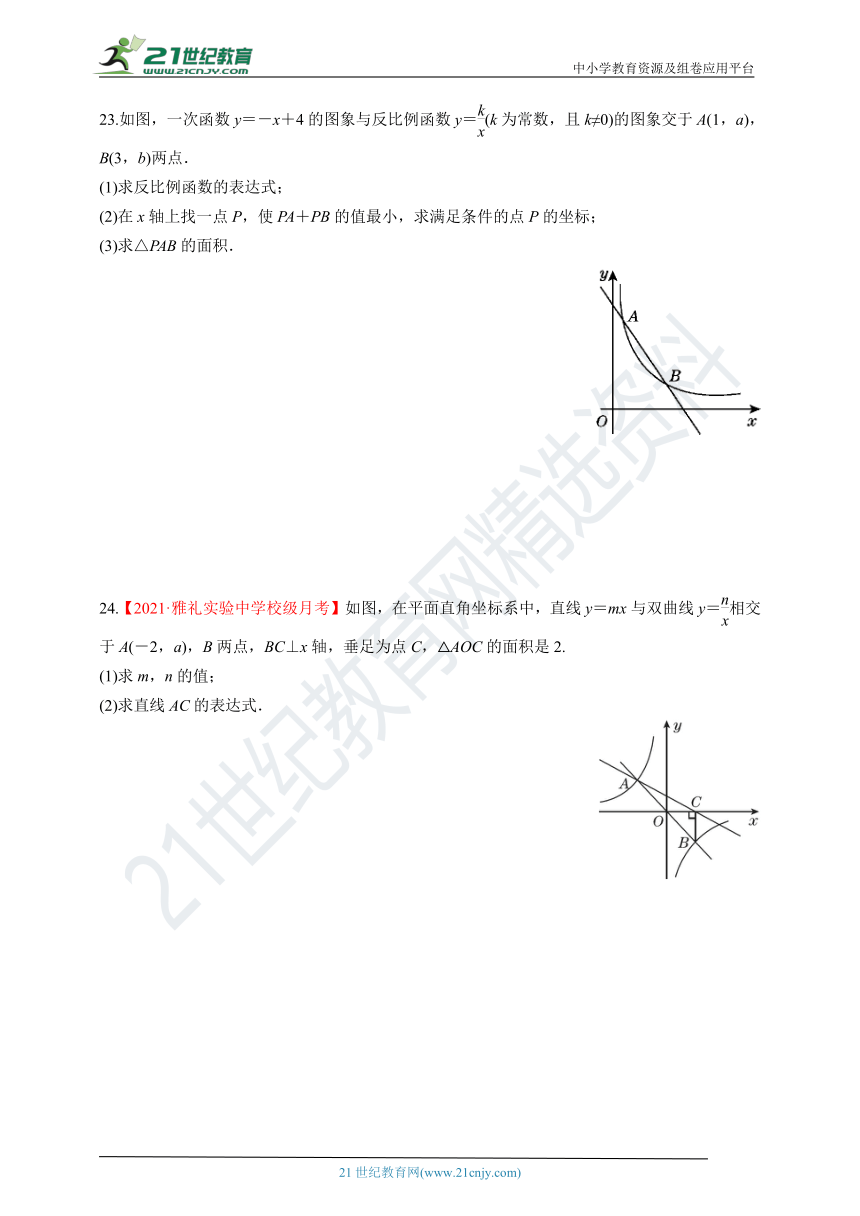
23.如图,一次函数y=-x+4的图象与反比例函数y=(k为常数,且k≠0)的图象交于A(1,a),B(3,b)两点.
(1)求反比例函数的表达式;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标;
(3)求△PAB的面积.
24.【2021·雅礼实验中学校级月考】如图,在平面直角坐标系中,直线y=mx与双曲线y=相交于A(-2,a),B两点,BC⊥x轴,垂足为点C,△AOC的面积是2.
(1)求m,n的值;
(2)求直线AC的表达式.
25.【2020·天水节选】如图所示,一次函数y=mx+n(m≠0)的图象与反比例函数y=(k≠0)的图象交于第二、四象限的点A(-2,a)和点B(b,-1),过A点作x轴的垂线,垂足为点C,△AOC的面积为4.
(1)分别求出a和b的值;
(2)在y轴上取点P,当PB-PA取得最大值时,求出点P的坐标.
中小学教育资源及组卷应用平台
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.【2019·哈尔滨】点(-1,4)在反比例函数y=的图象上,则下列各点在此函数图象上的是( A )
A.(4,-1)
B.
C.(-4,-1)
D.
2.【2021·江苏宿迁】已知双曲线过点(3,)、(1,)、(-2,),则下列结论正确的是(
A
)
A.
B.
C.
D.
【解析】∵
∴当x>0时,y随x的增大,且y<0;当x<0时,y随x的增大,且y>0;
∵0<1<3,-2<0
∴y2<y1<0,y3>0
∴.
3.如图,正方形ABOC的边长为2,反比例函数y=的图象经过点A,则k的值是
( D )
A.2
B.-2
C.4
D.-4
第3题图
第4题图
第6题图
第7题图
4.【2020·怀化】在同一平面直角坐标系中,一次函数y1=k1x+b与反比例函数y2=(x>0)的图象如图所示,则当y1>y2时,自变量x的取值范围为( D )
A.x<1
B.x>3
C.0D.15.【2020·新疆改编】一次函数y=mx-1和反比例函数y=在同一平面直角坐标系中的图象可能是( D )
6.【中考·湖州】如图,已知直线y=k1x(k1≠0)与反比例函数y=(k2≠0)的图象交于M,N两点.若点M的坐标是(1,2),则点N的坐标是( A )
A.(-1,-2)
B.(-1,2)
C.(1,-2)
D.(-2,-1)
7.如图,正方形ABCD的两个顶点B,D在反比例函数y=的图象上,对角线AC,BD的交点恰好是坐标原点O,已知B(-1,1),则k的值是( D )
A.-5
B.-4
C.-3
D.-1
8.【2019·株洲】如图,在平面直角坐标系xOy中,点A,B,C为反比例函数y=(k>0)图象上不同的三点,连接OA,OB,OC,过点A作AD⊥y轴于点D,过点B,C分别作BE,CF垂直于x轴于点E,F,OC与BE相交于点M,记△AOD,△BOM,四边形CMEF的面积分别为,,,则( )
A.=+S3
B.=S3
C.>>
D.<
第8题图
第9题图
第11题图
第12题图
【解析】∵点A,B,C为反比例函数y=(k>0)图象上不同的三点,AD⊥y轴,BE,CF垂直于x轴,∴S△AOD=S△BOE=S△COF=k.∴S△BOE-S△OME=S△COF-S△OME,∴S2=S3.故选B.
4.反比例函数y=的图象经过点M(-6,-2),则反比例函数的表达式为( D )
A.y=-
B.y=
C.y=-
D.y=
9.如图,在平面直角坐标系中,过x轴正半轴上任意一点P作y轴的平行线,分别交函数y=(x>0),y=-(x>0)的图象于点A,点B.若C是y轴上任意一点,则△ABC的面积为
( C )
A.9
B.6
C.
D.3
10.若点A(3,-2)关于y轴对称的点为B,则图象经过点B的反比例函数的表达式为( )
A.y=6x
B.y=-
C.y=-6x
D.y=
【点拨】设图象经过点B的反比例函数的表达式为y=(k≠0),则k=xy.∵点A(3,-2)关于y轴对称的点为B,∴点B的坐标为(-3,-2),把点B的坐标代入k=xy,得k=-3×(-2)=6.∴图象经过点B的反比例函数的表达式为y=.
【答案】D
11.如图,正方形ABCD的两个顶点B,D在反比例函数y=的图象上,对角线AC,BD的交点恰好是坐标原点O,已知B(-1,1),则k的值是( D )
A.-5
B.-4
C.-3
D.-1
12.【2020·张家界】如图所示,过y轴正半轴上的任意一点P作x轴的平行线,分别与反比例函数y=-和y=的图象交于点A和点B,若点C是x轴上任意一点,连接AC,BC,则△ABC的面积为( B )
A.6
B.7
C.8
D.14
13.【中考·通辽】关于x,y的二元一次方程组的解满足xA
B
C
D
【点拨】2x-3y=-4k与x-2y=k相减,得x-y=-5k,
∵关于x,y的二元一次方程组的解满足x<y,∴x-y<0,
∴-5k<0,即k>0,
∴直线y=kx-k-1经过第一、三、四象限,双曲线y=的两个分支位于第一、三象限,B选项符合,答案:B.
二、填空题
14.【2021·株洲】点A(x1,y1)、B(x1+1,y2)是反比例函数y=图象上的两点,满足:当x1>0时,均有y1<y2,则k的取值范围是
.
【解析】∵点A(x1,y1)、B(x1+1,y2)是反比例函数y=图象上的两点,
又∵0<x1<x1+1时,y1<y2,
∴函数图象在二四象限,
∴k<0,
【答案】k<0
15.【2020·青岛】如图,点A是反比例函数y=(x>0)图象上一点,AB垂直于x轴,垂足为B,△OAB的面积为6.若点P(a,7)也在此函数的图象上,则a=________.
【答案】
第15题图
第16题图
第17题图
第20题图
16.如图,过x轴正半轴上的任意一点P作y轴的平行线交反比例函数y=(x>0)和y=-(x>0)的图象于A,B两点,C是y轴上任意一点,则△ABC的面积为________.
【点拨】连接AO,BO,由题可得S△ABC=S△ABO=S△APO+S△BPO,
又易知S△APO=×2=1,
S△BPO=×|-4|=2,∴S△ABC=3.
【答案】3
17.【中考·邵阳】如图,在平面直角坐标系中,点A的坐标为(-4,2),反比例函数y=(x<0)的图象经过线段OA的中点B,则k=________.
【点拨】如图,过点B作BD⊥x轴于D,BF⊥y轴于F.
∵AC∥BD,B是OA的中点,∴OD=DC,同理得OF=EF.
∵A(-4,2),∴AC=2,OC=4,
∴OD=CD=2,BD=OF=EF=1,
∴B(-2,1),代入y=得1=,
∴k=-2×1=-2.
【答案】-2
18.【中考·北京】在平面直角坐标系xOy中,点A(a,b)(a>0,b>0)在双曲线y=上,点A关于x轴的对称点B在双曲线y=上,则k1+k2的值为________.
【点拨】∵点A(a,b)(a>0,b>0)在双曲线y=上,∴k1=ab.
又∵点A与点B关于x轴对称,∴B(a,-b).
∵点B在双曲线y=上,∴k2=-ab.
∴k1+k2=ab+(-ab)=0.
【答案】0
19.在反比例函数y=的图象上有两点A(x1,y1),B(x2,y2),当x1<0【答案】m>-
20.如图,在平面直角坐标系中,△ABC的顶点A和C分别在x轴、y轴的正半轴上,且AB∥y轴,AB=4,△ABC的面积为2,将△ABC以点B为旋转中心,顺时针旋转90°得到△DBE,一个反比例函数的图象恰好过点D,则此反比例函数的表达式是__________________________.
【点拨】∵AB∥y轴,AB=4,△ABC的面积为2,
∴S△ABC=AB·OA=×4×OA=2OA=2,∴OA=1,∴B(1,4).
∵将△ABC以点B为旋转中心,顺时针旋转90°得到△DBE,
∴BD=AB=4,∠ABD=90°,∴DB∥x轴,
设DB与y轴交于点F,∴DF=DB-BF=4-1=3,
∴D(-3,4),设反比例函数的表达式为y=,
∴k=-3×4=-12.
∴此反比例函数的表达式是y=-.
【答案】y=-
三、解答题
21.如图,一次函数y=kx+b的图象与反比例函数y=的图象交于点A(-2,-5),C(5,n),交y轴于点B,交x轴于点D.
(1)求反比例函数y=和一次函数y=kx+b的表达式;
(2)连接OA,OC.求△AOC的面积.
解:(1)把A(-2,-5)代入y=,得-5=,
解得m=10,则反比例函数的表达式是y=,
把x=5代入y=,得y=2,则C的坐标是(5,2).
根据题意,得解得
则一次函数的表达式是y=x-3.
(2)在y=x-3中,令x=0,解得y=-3.
则B的坐标是(0,-3).
∴OB=3,
∵点A的横坐标是-2,C的横坐标是5.
∴S△AOC=S△AOB+S△BOC=OB×2+OB×5=×3×7=.
22.【2020·菏泽】如图,一次函数y=kx+b的图象与反比例函数y=的图象相交于A(1,2),B(n,-1)两点.
(1)求一次函数和反比例函数的表达式;
解:将点A(1,2)的坐标代入y=,得m=2,
∴反比例函数的表达式为y=.
将点B(n,-1)的坐标代入y=,得n=-2,∴B(-2,-1).
将点A(1,2),B(-2,-1)的坐标代入y=kx+b,
得解得
∴一次函数的表达式为y=x+1.
(2)直线AB交x轴于点C,点P是x轴上的点,若△ACP的面积是4,求点P的坐标.
解:设点P(a,0),
∵直线AB交x轴于点C,∴易得C(-1,0),
∴PC=|a+1|.
∵△ACP的面积是4,∴易得×|a+1|×2=4,
解得a1=3,a2=-5,∴点P的坐标为(3,0)或(-5,0).
23.如图,一次函数y=-x+4的图象与反比例函数y=(k为常数,且k≠0)的图象交于A(1,a),B(3,b)两点.
(1)求反比例函数的表达式;
解:把点A(1,a)的坐标代入y=-x+4,
得a=-1+4,解得a=3,
∴A(1,3),把(1,3)代入y=,得k=3,
∴反比例函数的表达式为y=.
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标;
解:把B(3,b)的坐标代入反比例函数的表达式,得B(3,1).
如图,作点B关于x轴的对称点D,交x轴于点C,连接AD,交x轴于点P,连接PB,此时PA+PB的值最小.
易得D(3,-1).
设直线AD的表达式为y=mx+n,
把A,D两点的坐标代入,得解得
∴直线AD的表达式为y=-2x+5.
令y=0,得x=,
∴点P的坐标为.
(3)求△PAB的面积.
解:S△PAB=S△ABD-S△PBD=×[1-(-1)]×(3-1)-×[1-(-1)]×=×2×2-×2×=2-=1.5.
24.【2021·雅礼实验中学校级月考】如图,在平面直角坐标系中,直线y=mx与双曲线y=相交于A(-2,a),B两点,BC⊥x轴,垂足为点C,△AOC的面积是2.
(1)求m,n的值;
解:∵直线y=mx与双曲线y=相交于A(-2,a),B两点,∴点A与点B关于原点对称.
∴B(2,-a).∴C(2,0).
∵S△AOC=2,∴×2×a=2,解得a=2.∴A(-2,2).
把点A(-2,2)的坐标分别代入y=mx和y=,得-2m=2,2=,解得m=-1,n=-4.
(2)求直线AC的表达式.
解:设直线AC的表达式为y=kx+b.
∵直线AC经过点A,C,
∴解得
∴直线AC的表达式为y=-x+1.
25.【2020·天水节选】如图所示,一次函数y=mx+n(m≠0)的图象与反比例函数y=(k≠0)的图象交于第二、四象限的点A(-2,a)和点B(b,-1),过A点作x轴的垂线,垂足为点C,△AOC的面积为4.
(1)分别求出a和b的值;
解:∵△AOC的面积为4,∴|k|=4,
解得k=-8或k=8(不符合题意,舍去).
∴反比例函数的表达式为y=-.
把点A(-2,a)和点B(b,-1)的坐标分别代入y=-,得a=4,b=8.
(2)在y轴上取点P,当PB-PA取得最大值时,求出点P的坐标.
解:设点A(-2,4)关于y轴的对称点为A′,则A′的坐标为(2,4),连接BA′并延长,交y轴于点P,连接PA,此时PB-PA的值最大.
设直线A′B对应的函数表达式为y=cx+d,
则有解得
∴直线A′B对应的函数表达式为y=-x+.
∴直线y=-x+与y轴的交点坐标为,
即点P的坐标为.
第3课时
反比例函数的图象与性质的综合应用
一、选择题
1.【2019·哈尔滨】点(-1,4)在反比例函数y=的图象上,则下列各点在此函数图象上的是( )
A.(4,-1)
B.
C.(-4,-1)
D.
2.【2021·江苏宿迁】已知双曲线过点(3,)、(1,)、(-2,),则下列结论正确的是(
)
A.
B.
C.
D.
3.如图,正方形ABOC的边长为2,反比例函数y=的图象经过点A,则k的值是
( )
A.2
B.-2
C.4
D.-4
第3题图
第4题图
第6题图
第7题图
4.【2020·怀化】在同一平面直角坐标系中,一次函数y1=k1x+b与反比例函数y2=(x>0)的图象如图所示,则当y1>y2时,自变量x的取值范围为( )
A.x<1
B.x>3
C.0
6.【中考·湖州】如图,已知直线y=k1x(k1≠0)与反比例函数y=(k2≠0)的图象交于M,N两点.若点M的坐标是(1,2),则点N的坐标是( )
A.(-1,-2)
B.(-1,2)
C.(1,-2)
D.(-2,-1)
7.如图,正方形ABCD的两个顶点B,D在反比例函数y=的图象上,对角线AC,BD的交点恰好是坐标原点O,已知B(-1,1),则k的值是( )
A.-5
B.-4
C.-3
D.-1
8.【2019·株洲】如图,在平面直角坐标系xOy中,点A,B,C为反比例函数y=(k>0)图象上不同的三点,连接OA,OB,OC,过点A作AD⊥y轴于点D,过点B,C分别作BE,CF垂直于x轴于点E,F,OC与BE相交于点M,记△AOD,△BOM,四边形CMEF的面积分别为,,,则( )
A.=+S3
B.=S3
C.>>
D.<
第8题图
第9题图
第11题图
第12题图
4.反比例函数y=的图象经过点M(-6,-2),则反比例函数的表达式为( )
A.y=-
B.y=
C.y=-
D.y=
9.如图,在平面直角坐标系中,过x轴正半轴上任意一点P作y轴的平行线,分别交函数y=(x>0),y=-(x>0)的图象于点A,点B.若C是y轴上任意一点,则△ABC的面积为
( )
A.9
B.6
C.
D.3
10.若点A(3,-2)关于y轴对称的点为B,则图象经过点B的反比例函数的表达式为( )
A.y=6x
B.y=-
C.y=-6x
D.y=
11.如图,正方形ABCD的两个顶点B,D在反比例函数y=的图象上,对角线AC,BD的交点恰好是坐标原点O,已知B(-1,1),则k的值是( )
A.-5
B.-4
C.-3
D.-1
12.【2020·张家界】如图所示,过y轴正半轴上的任意一点P作x轴的平行线,分别与反比例函数y=-和y=的图象交于点A和点B,若点C是x轴上任意一点,连接AC,BC,则△ABC的面积为( )
A.6
B.7
C.8
D.14
13.【中考·通辽】关于x,y的二元一次方程组的解满足x
B
C
D
二、填空题
14.【2021·株洲】点A(x1,y1)、B(x1+1,y2)是反比例函数y=图象上的两点,满足:当x1>0时,均有y1<y2,则k的取值范围是
.
15.【2020·青岛】如图,点A是反比例函数y=(x>0)图象上一点,AB垂直于x轴,垂足为B,△OAB的面积为6.若点P(a,7)也在此函数的图象上,则a=________.
第15题图
第16题图
第17题图
第20题图
16.如图,过x轴正半轴上的任意一点P作y轴的平行线交反比例函数y=(x>0)和y=-(x>0)的图象于A,B两点,C是y轴上任意一点,则△ABC的面积为________.
17.【中考·邵阳】如图,在平面直角坐标系中,点A的坐标为(-4,2),反比例函数y=(x<0)的图象经过线段OA的中点B,则k=________.
18.【中考·北京】在平面直角坐标系xOy中,点A(a,b)(a>0,b>0)在双曲线y=上,点A关于x轴的对称点B在双曲线y=上,则k1+k2的值为________.
19.在反比例函数y=的图象上有两点A(x1,y1),B(x2,y2),当x1<0
三、解答题
21.如图,一次函数y=kx+b的图象与反比例函数y=的图象交于点A(-2,-5),C(5,n),交y轴于点B,交x轴于点D.
(1)求反比例函数y=和一次函数y=kx+b的表达式;
(2)连接OA,OC.求△AOC的面积.
22.【2020·菏泽】如图,一次函数y=kx+b的图象与反比例函数y=的图象相交于A(1,2),B(n,-1)两点.
(1)求一次函数和反比例函数的表达式;
(2)直线AB交x轴于点C,点P是x轴上的点,若△ACP的面积是4,求点P的坐标.
23.如图,一次函数y=-x+4的图象与反比例函数y=(k为常数,且k≠0)的图象交于A(1,a),B(3,b)两点.
(1)求反比例函数的表达式;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标;
(3)求△PAB的面积.
24.【2021·雅礼实验中学校级月考】如图,在平面直角坐标系中,直线y=mx与双曲线y=相交于A(-2,a),B两点,BC⊥x轴,垂足为点C,△AOC的面积是2.
(1)求m,n的值;
(2)求直线AC的表达式.
25.【2020·天水节选】如图所示,一次函数y=mx+n(m≠0)的图象与反比例函数y=(k≠0)的图象交于第二、四象限的点A(-2,a)和点B(b,-1),过A点作x轴的垂线,垂足为点C,△AOC的面积为4.
(1)分别求出a和b的值;
(2)在y轴上取点P,当PB-PA取得最大值时,求出点P的坐标.
中小学教育资源及组卷应用平台
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.【2019·哈尔滨】点(-1,4)在反比例函数y=的图象上,则下列各点在此函数图象上的是( A )
A.(4,-1)
B.
C.(-4,-1)
D.
2.【2021·江苏宿迁】已知双曲线过点(3,)、(1,)、(-2,),则下列结论正确的是(
A
)
A.
B.
C.
D.
【解析】∵
∴当x>0时,y随x的增大,且y<0;当x<0时,y随x的增大,且y>0;
∵0<1<3,-2<0
∴y2<y1<0,y3>0
∴.
3.如图,正方形ABOC的边长为2,反比例函数y=的图象经过点A,则k的值是
( D )
A.2
B.-2
C.4
D.-4
第3题图
第4题图
第6题图
第7题图
4.【2020·怀化】在同一平面直角坐标系中,一次函数y1=k1x+b与反比例函数y2=(x>0)的图象如图所示,则当y1>y2时,自变量x的取值范围为( D )
A.x<1
B.x>3
C.0
6.【中考·湖州】如图,已知直线y=k1x(k1≠0)与反比例函数y=(k2≠0)的图象交于M,N两点.若点M的坐标是(1,2),则点N的坐标是( A )
A.(-1,-2)
B.(-1,2)
C.(1,-2)
D.(-2,-1)
7.如图,正方形ABCD的两个顶点B,D在反比例函数y=的图象上,对角线AC,BD的交点恰好是坐标原点O,已知B(-1,1),则k的值是( D )
A.-5
B.-4
C.-3
D.-1
8.【2019·株洲】如图,在平面直角坐标系xOy中,点A,B,C为反比例函数y=(k>0)图象上不同的三点,连接OA,OB,OC,过点A作AD⊥y轴于点D,过点B,C分别作BE,CF垂直于x轴于点E,F,OC与BE相交于点M,记△AOD,△BOM,四边形CMEF的面积分别为,,,则( )
A.=+S3
B.=S3
C.>>
D.<
第8题图
第9题图
第11题图
第12题图
【解析】∵点A,B,C为反比例函数y=(k>0)图象上不同的三点,AD⊥y轴,BE,CF垂直于x轴,∴S△AOD=S△BOE=S△COF=k.∴S△BOE-S△OME=S△COF-S△OME,∴S2=S3.故选B.
4.反比例函数y=的图象经过点M(-6,-2),则反比例函数的表达式为( D )
A.y=-
B.y=
C.y=-
D.y=
9.如图,在平面直角坐标系中,过x轴正半轴上任意一点P作y轴的平行线,分别交函数y=(x>0),y=-(x>0)的图象于点A,点B.若C是y轴上任意一点,则△ABC的面积为
( C )
A.9
B.6
C.
D.3
10.若点A(3,-2)关于y轴对称的点为B,则图象经过点B的反比例函数的表达式为( )
A.y=6x
B.y=-
C.y=-6x
D.y=
【点拨】设图象经过点B的反比例函数的表达式为y=(k≠0),则k=xy.∵点A(3,-2)关于y轴对称的点为B,∴点B的坐标为(-3,-2),把点B的坐标代入k=xy,得k=-3×(-2)=6.∴图象经过点B的反比例函数的表达式为y=.
【答案】D
11.如图,正方形ABCD的两个顶点B,D在反比例函数y=的图象上,对角线AC,BD的交点恰好是坐标原点O,已知B(-1,1),则k的值是( D )
A.-5
B.-4
C.-3
D.-1
12.【2020·张家界】如图所示,过y轴正半轴上的任意一点P作x轴的平行线,分别与反比例函数y=-和y=的图象交于点A和点B,若点C是x轴上任意一点,连接AC,BC,则△ABC的面积为( B )
A.6
B.7
C.8
D.14
13.【中考·通辽】关于x,y的二元一次方程组的解满足x
B
C
D
【点拨】2x-3y=-4k与x-2y=k相减,得x-y=-5k,
∵关于x,y的二元一次方程组的解满足x<y,∴x-y<0,
∴-5k<0,即k>0,
∴直线y=kx-k-1经过第一、三、四象限,双曲线y=的两个分支位于第一、三象限,B选项符合,答案:B.
二、填空题
14.【2021·株洲】点A(x1,y1)、B(x1+1,y2)是反比例函数y=图象上的两点,满足:当x1>0时,均有y1<y2,则k的取值范围是
.
【解析】∵点A(x1,y1)、B(x1+1,y2)是反比例函数y=图象上的两点,
又∵0<x1<x1+1时,y1<y2,
∴函数图象在二四象限,
∴k<0,
【答案】k<0
15.【2020·青岛】如图,点A是反比例函数y=(x>0)图象上一点,AB垂直于x轴,垂足为B,△OAB的面积为6.若点P(a,7)也在此函数的图象上,则a=________.
【答案】
第15题图
第16题图
第17题图
第20题图
16.如图,过x轴正半轴上的任意一点P作y轴的平行线交反比例函数y=(x>0)和y=-(x>0)的图象于A,B两点,C是y轴上任意一点,则△ABC的面积为________.
【点拨】连接AO,BO,由题可得S△ABC=S△ABO=S△APO+S△BPO,
又易知S△APO=×2=1,
S△BPO=×|-4|=2,∴S△ABC=3.
【答案】3
17.【中考·邵阳】如图,在平面直角坐标系中,点A的坐标为(-4,2),反比例函数y=(x<0)的图象经过线段OA的中点B,则k=________.
【点拨】如图,过点B作BD⊥x轴于D,BF⊥y轴于F.
∵AC∥BD,B是OA的中点,∴OD=DC,同理得OF=EF.
∵A(-4,2),∴AC=2,OC=4,
∴OD=CD=2,BD=OF=EF=1,
∴B(-2,1),代入y=得1=,
∴k=-2×1=-2.
【答案】-2
18.【中考·北京】在平面直角坐标系xOy中,点A(a,b)(a>0,b>0)在双曲线y=上,点A关于x轴的对称点B在双曲线y=上,则k1+k2的值为________.
【点拨】∵点A(a,b)(a>0,b>0)在双曲线y=上,∴k1=ab.
又∵点A与点B关于x轴对称,∴B(a,-b).
∵点B在双曲线y=上,∴k2=-ab.
∴k1+k2=ab+(-ab)=0.
【答案】0
19.在反比例函数y=的图象上有两点A(x1,y1),B(x2,y2),当x1<0
20.如图,在平面直角坐标系中,△ABC的顶点A和C分别在x轴、y轴的正半轴上,且AB∥y轴,AB=4,△ABC的面积为2,将△ABC以点B为旋转中心,顺时针旋转90°得到△DBE,一个反比例函数的图象恰好过点D,则此反比例函数的表达式是__________________________.
【点拨】∵AB∥y轴,AB=4,△ABC的面积为2,
∴S△ABC=AB·OA=×4×OA=2OA=2,∴OA=1,∴B(1,4).
∵将△ABC以点B为旋转中心,顺时针旋转90°得到△DBE,
∴BD=AB=4,∠ABD=90°,∴DB∥x轴,
设DB与y轴交于点F,∴DF=DB-BF=4-1=3,
∴D(-3,4),设反比例函数的表达式为y=,
∴k=-3×4=-12.
∴此反比例函数的表达式是y=-.
【答案】y=-
三、解答题
21.如图,一次函数y=kx+b的图象与反比例函数y=的图象交于点A(-2,-5),C(5,n),交y轴于点B,交x轴于点D.
(1)求反比例函数y=和一次函数y=kx+b的表达式;
(2)连接OA,OC.求△AOC的面积.
解:(1)把A(-2,-5)代入y=,得-5=,
解得m=10,则反比例函数的表达式是y=,
把x=5代入y=,得y=2,则C的坐标是(5,2).
根据题意,得解得
则一次函数的表达式是y=x-3.
(2)在y=x-3中,令x=0,解得y=-3.
则B的坐标是(0,-3).
∴OB=3,
∵点A的横坐标是-2,C的横坐标是5.
∴S△AOC=S△AOB+S△BOC=OB×2+OB×5=×3×7=.
22.【2020·菏泽】如图,一次函数y=kx+b的图象与反比例函数y=的图象相交于A(1,2),B(n,-1)两点.
(1)求一次函数和反比例函数的表达式;
解:将点A(1,2)的坐标代入y=,得m=2,
∴反比例函数的表达式为y=.
将点B(n,-1)的坐标代入y=,得n=-2,∴B(-2,-1).
将点A(1,2),B(-2,-1)的坐标代入y=kx+b,
得解得
∴一次函数的表达式为y=x+1.
(2)直线AB交x轴于点C,点P是x轴上的点,若△ACP的面积是4,求点P的坐标.
解:设点P(a,0),
∵直线AB交x轴于点C,∴易得C(-1,0),
∴PC=|a+1|.
∵△ACP的面积是4,∴易得×|a+1|×2=4,
解得a1=3,a2=-5,∴点P的坐标为(3,0)或(-5,0).
23.如图,一次函数y=-x+4的图象与反比例函数y=(k为常数,且k≠0)的图象交于A(1,a),B(3,b)两点.
(1)求反比例函数的表达式;
解:把点A(1,a)的坐标代入y=-x+4,
得a=-1+4,解得a=3,
∴A(1,3),把(1,3)代入y=,得k=3,
∴反比例函数的表达式为y=.
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标;
解:把B(3,b)的坐标代入反比例函数的表达式,得B(3,1).
如图,作点B关于x轴的对称点D,交x轴于点C,连接AD,交x轴于点P,连接PB,此时PA+PB的值最小.
易得D(3,-1).
设直线AD的表达式为y=mx+n,
把A,D两点的坐标代入,得解得
∴直线AD的表达式为y=-2x+5.
令y=0,得x=,
∴点P的坐标为.
(3)求△PAB的面积.
解:S△PAB=S△ABD-S△PBD=×[1-(-1)]×(3-1)-×[1-(-1)]×=×2×2-×2×=2-=1.5.
24.【2021·雅礼实验中学校级月考】如图,在平面直角坐标系中,直线y=mx与双曲线y=相交于A(-2,a),B两点,BC⊥x轴,垂足为点C,△AOC的面积是2.
(1)求m,n的值;
解:∵直线y=mx与双曲线y=相交于A(-2,a),B两点,∴点A与点B关于原点对称.
∴B(2,-a).∴C(2,0).
∵S△AOC=2,∴×2×a=2,解得a=2.∴A(-2,2).
把点A(-2,2)的坐标分别代入y=mx和y=,得-2m=2,2=,解得m=-1,n=-4.
(2)求直线AC的表达式.
解:设直线AC的表达式为y=kx+b.
∵直线AC经过点A,C,
∴解得
∴直线AC的表达式为y=-x+1.
25.【2020·天水节选】如图所示,一次函数y=mx+n(m≠0)的图象与反比例函数y=(k≠0)的图象交于第二、四象限的点A(-2,a)和点B(b,-1),过A点作x轴的垂线,垂足为点C,△AOC的面积为4.
(1)分别求出a和b的值;
解:∵△AOC的面积为4,∴|k|=4,
解得k=-8或k=8(不符合题意,舍去).
∴反比例函数的表达式为y=-.
把点A(-2,a)和点B(b,-1)的坐标分别代入y=-,得a=4,b=8.
(2)在y轴上取点P,当PB-PA取得最大值时,求出点P的坐标.
解:设点A(-2,4)关于y轴的对称点为A′,则A′的坐标为(2,4),连接BA′并延长,交y轴于点P,连接PA,此时PB-PA的值最大.
设直线A′B对应的函数表达式为y=cx+d,
则有解得
∴直线A′B对应的函数表达式为y=-x+.
∴直线y=-x+与y轴的交点坐标为,
即点P的坐标为.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
