第四章图形认识初步学案
图片预览

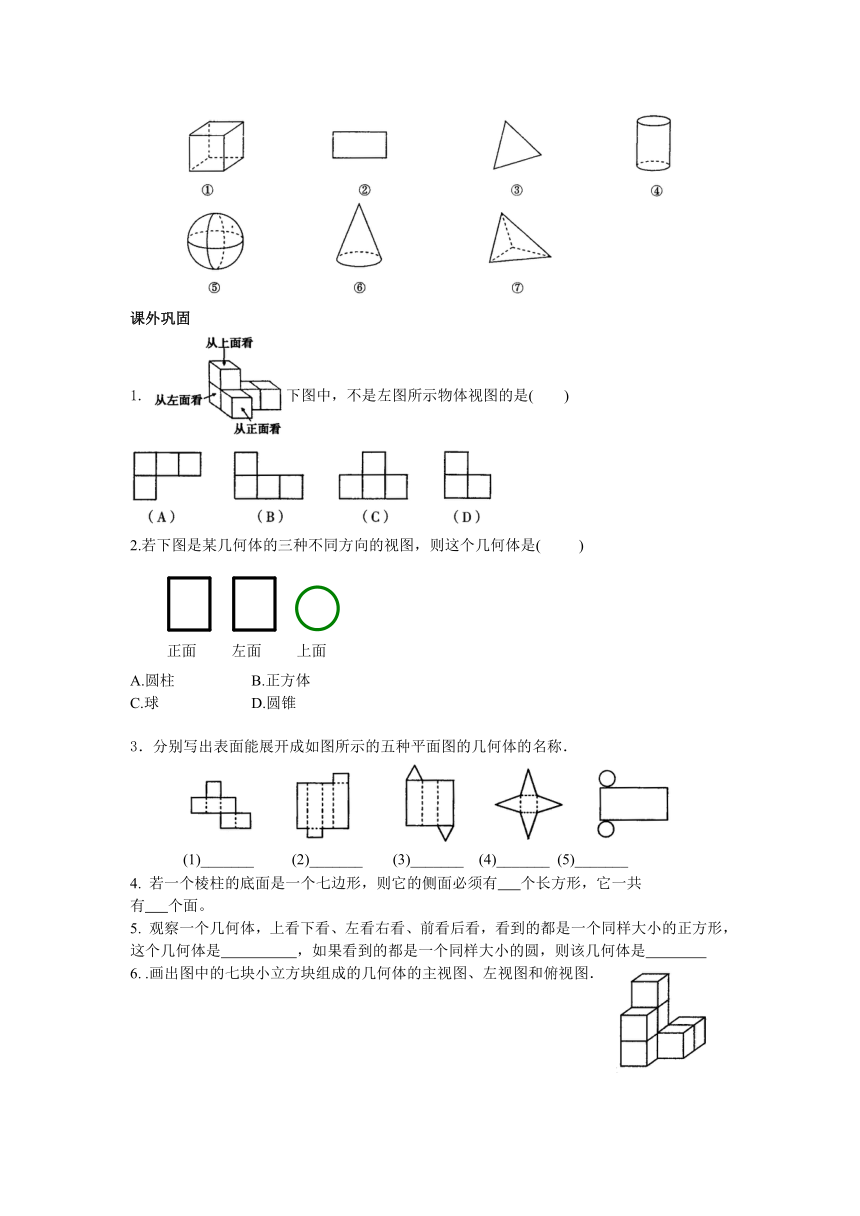

文档简介
4.1.1 几何图形
名师归纳与点拨
知识点1 几何图形可分为平面图形和立体图形
平面图形的定义:各部分都在同一平面的图形。
立体图形的定义:具有长、宽、高的物体。
说明:长方形、正方形、三角形、圆等都是我们十分熟悉的平面图形;长方体、正方体、球、圆柱、圆锥等都是立体图形.
知识点2 立体图形和平面图形的转化
一个立体图形从不同方向看,可以是一个平面图形;可以把立体图形进行适当的裁剪,把它展开成平面图形,或者把一个平面图形复原成立体图形,即立体图形与平面图形可以互相转换.
说明: ①在画三视图时一般要求“长对正,高平齐,宽相等”。②不是所有的立体图形都可以展开,例如球体便不可以展开。
例1:下列几种图形:①长方形;②梯形;③正方体;④圆柱;⑤圆锥;.其中属于立体图形的是( )
A. ①②③;B. ③④⑤;C. ③⑤;D.④⑤
思路导引 根据几何图形的各部分不都在同一平面内,具有长、宽、高,那么此几何图形就是一个立体图形来进行判断。
解:选B
例2:如图4-1-1,表示一个用于防震的形的包装用泡沫塑料,当从上面看这一物体时看到的图形形状是( )
思路导引 从上往下看此物体得到的是它的俯视图,注意“看得见的轮廓线用实线,看不见的轮廓线用虚线”。
解:选B
课内达标
1. 一个正方体的平面展开图如图所示,将它折成正方体后“建”字对面是( )
A.和 B.谐
C.昆 D.明
2. 圆柱的侧面展开图是_______形。
3.主视图、左视图、俯视图都一样的几何体为________
4. 下图中哪些图形是立体的,哪些是平面的
课外巩固
1. 下图中,不是左图所示物体视图的是( )
2.若下图是某几何体的三种不同方向的视图,则这个几何体是( )
A.圆柱 B.正方体
C.球 D.圆锥
3.分别写出表面能展开成如图所示的五种平面图的几何体的名称.
(1)_______ (2)_______ (3)_______ (4)_______ (5)_______
4. 若一个棱柱的底面是一个七边形,则它的侧面必须有 个长方形,它一共
有 个面。
5. 观察一个几何体,上看下看、左看右看、前看后看,看到的都是一个同样大小的正方形,这个几何体是 ,如果看到的都是一个同样大小的圆,则该几何体是
6. .画出图中的七块小立方块组成的几何体的主视图、左视图和俯视图.
7.如图是一个正方体的展开图,标注了字母A的面是正方体的正面,设正方体的左面与右面所标注的代数式的值相等,求x的值。
8. 如图,沿长方形纸片上的边线剪下的阴影部分,恰好能围成一圆柱,设圆半径为r
(1)用含r的代数式表示圆柱的体积; 中间的四边形是正方形
(2)当r=3,圆周率取3.14时,求圆柱的体积(保留整数)。
4.1.2 几何图形
名师归纳与点拨
知识点1 点、线、面、体组成几何图形,点是构成图形的基本元素。
包围着体的是面,面与面相交的地方时线,线与线相交的地方是点。
说明:点、线、面、体之间有如图所示的联系:
例1 :圆锥可以看作是由一个_______旋转得到的( )
A.矩形(长方形) B.等腰梯形
C.半圆 D.直角三角形
思路导引 利用一个三角板绕其直角边旋转即可得到答案。
解:选D
课内达标
1、面和面相交成( )
A、点 B、线 C、面 D、体
2、点动成______;线动成______;面动成_______。
3、飞机飞行表演时在空中留下漂亮的“彩带”。用数学知识解释为___________。
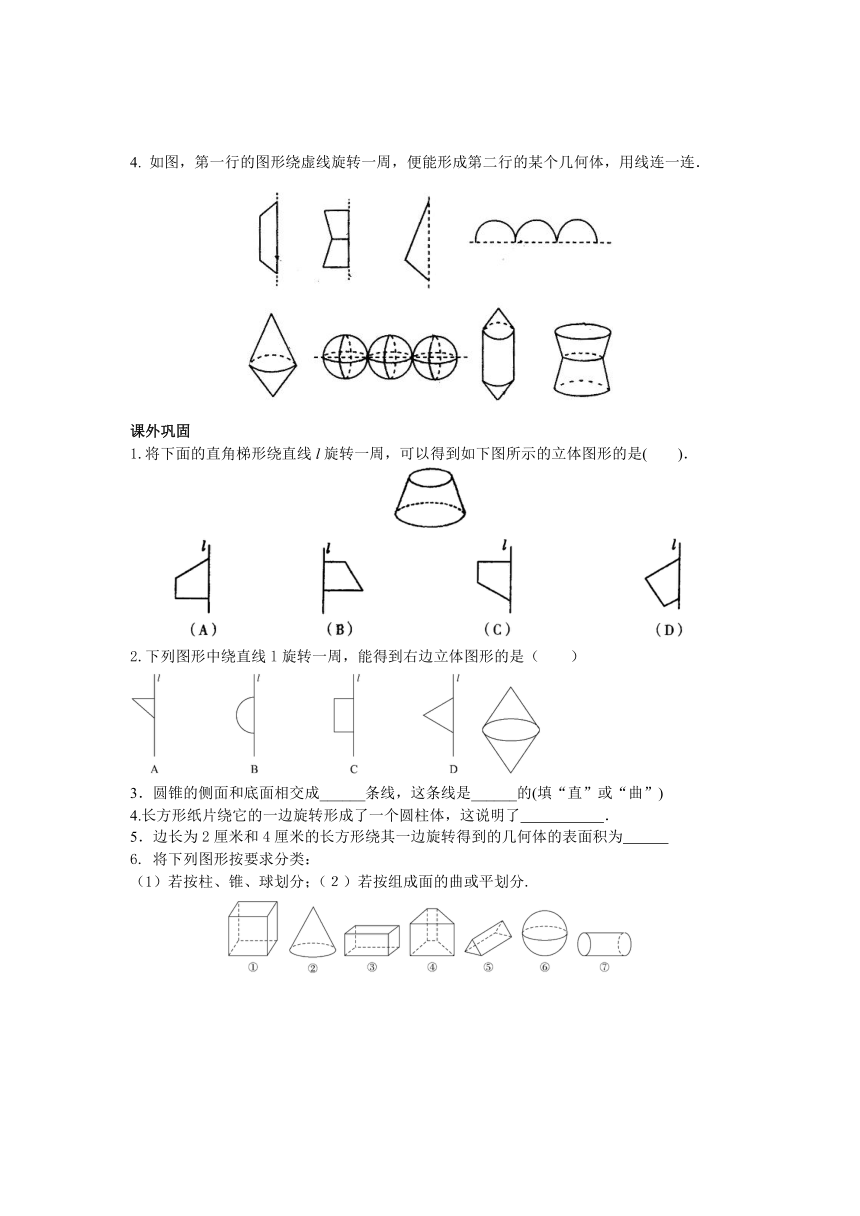
4. 如图,第一行的图形绕虚线旋转一周,便能形成第二行的某个几何体,用线连一连.
课外巩固
1.将下面的直角梯形绕直线l旋转一周,可以得到如下图所示的立体图形的是( ).
2.下列图形中绕直线l旋转一周,能得到右边立体图形的是( )
3.圆锥的侧面和底面相交成______条线,这条线是______的(填“直”或“曲”)
4.长方形纸片绕它的一边旋转形成了一个圆柱体,这说明了 .
5.边长为2厘米和4厘米的长方形绕其一边旋转得到的几何体的表面积为
6. 将下列图形按要求分类:
(1)若按柱、锥、球划分;(2)若按组成面的曲或平划分.
7. 第二行的图绕直线旋转一周,便能形成第一行的某个几何体,用线连一连,并指出这些几何体的名称.
8.将一个长方形绕它的一边所在的直线旋转一周,得到的几何体是圆柱,现在有一个长为4厘米,宽为3厘米的长方形,分别绕它的长、宽所在的直线旋转一周,得到不同的圆柱体,它们的体积分别是多大?
4.2.1直线、线段、射线
第一课时
名师归纳与点拨
知识点1直线、线段、射线的概念及表示
1.直线是向两个方向无限延伸着的;直线上两个点和它们之间的部分叫做线段;直线上的一点和它一旁的部分叫做射线。
2.表示方法:①直线的表示有两种:一个小写字母或两个大写字母.但前面必须加“直线”两字,如:直线l;直线m,直线AB;直线CD. ②线段的表示也有两种:一个小写字母或用端点的两个大写字母.但前面必须加“线段”两字.如:线段a;线段AB.③射线的表示同样有两种:一个小写字母或端点的大写字母和射线上的一个大写字母,前面必须加“射线”两字.如:射线a;射线OA.
说明:直线和射线都不可度量,而线段可度量。用两个大写字母表示射线时注意端点字母要写在前。
知识点2:直线的基本性质:经过两点有一条并且只有一条直线
说明: 这条性质也被称为“直线公理”。“有”表示“存在性”,“只有”表示“唯一性”。
例1 判断下列说法是否正确
1.射线EO和射线OE是同一条射线( )
2.直线比射线长 ( )
3.延长射线OA到B ( )
4.线段AB与线段BA是同一条线段 ( )
思路导引 1.两个大写字母表示射线时,端点字母要在前;2.直线和射线都不可度量;3.射线不可度量;4.线段有两个端点,用两个大写字母表示时与端点字母顺序无关。
解:1.错 2.错 3.错 4.正确
例2.下面图形有几条线段?
思路导引:方法一:以线段的端点为顺序,从左向右观察以A为左端点的线段有几条?AB、AC、AD一共有三条。以B为左端点的线段有几条?BC、BD一共有两条。以C为左端点的线段有几条?一条。
解:3+ 2+ 1=6(条)
课内达标
1. 下面几种表示直线的写法中,错误的是( ).
A.直线a B.直线Ma C.直线MN D.直线MO
2. 在墙上钉一根木条需_______个钉子,其根据是________ .
3. 如图所示,直线_______和直线______相交于点P;直线AB和直线EF相交于点______;点R是直线________和直线________的交点.
4. 探索规律:
(1)若直线L上有2个点,则射线有_____条,线段有______条; ( http: / / www. / / )
(2)若直线L上有3个点,则射线有_____条,线段有______条;
(3)若直线L上有4个点,则射线有_____条,线段有______条;
(4)若直线L上有n个点,则射线有_____条,线段有______条.
课外巩固
1. 下列说法中,正确的是( )
A.射线OA和射线AO表示同一条射线.
B.延长直线AB.
C.经过两点有一条直线,并且只有一条直线.
D.延长射线AB
2.下列四个图中的线段(或直线、射线)能相交的是( )
`
A.(1) B.(2) C.(3) D.(4)
3. 如下图所示,点A在直线L______,点B在直线L________.
4. 如图2,图中共有_______条射线,指出其中的两条_____ __.
5. 如图,OA反向延长得射线 ______
6.看图写话:
(1) (2)
7.如图,要在一个长方体的木块上打四个小孔,这四个小孔要在一条直线上,且每两个相邻孔之间的距离相等,画出图形,并说明其中道理.
8.解答下列问题:
(1) 画图表示,两条直线可以把一个平面分成几个部分 三条直线呢
(2)平面上4条直线最多可以把平面分成多少个部分
4.2.2直线、线段、射线
第二课时
名师归纳与点拨
知识点1线段大小比较的两种比较方法:
重叠比较法 将两条线段的各一个端点对齐,看另一个端点的位置.
数量比较法 用刻度尺分别量出线段AB和线段CD的长度,将长度进行比较.
说明:常用的是数量比较法。
知识点2 线段的性质公理
“两点之间的所有连线中,线段最短”
说明:要强调两点之间的线段的长度叫两点间的距离,而不是两点间的线段;
线段是图形,线段的长度是数值。
例1.点P是线段AB的中点,点C、D把线段AB三等分。已知线段CP的长为1.5cm,求线段AB的长。
思路导引 先得到线段CP与线段AB之间的长度比,就能求出线段AB的长。
解:∵ 点P把线段二等分,
∴ AP=PB=1/2AB
∵ 点C、D把线段AB三等分,
∴ AC=CD=DB=1/3AB
∴ AP-AC=1/2AB-1/3AB=1/6AB, 即 CP=1/6AB
∴ AB=6CP=6×1.5=9cm
即AB的长为9cm
课内达标
1. 在直线上顺次取A、B、C三点,使得AB=5㎝,BC=3㎝,如果O是线段AC的中点,那么线段OB的长度是( )
A.2㎝ B.0.5㎝ C.1.5㎝ D. 1㎝
2. 如图,学生要去博物馆参观,从学校A处到博物馆B处的路径共有⑴、⑵、⑶三条,为了节约时间,尽快从A处赶到B处,假设行走的速度不变,你认为应该走第________条线路(只填番号)最快,理由是___________________。
3.若AB=BC=CD那么AD= AB AC= AD
4. 线段AD=6cm,线段AC=BD=4cm ,E、F分别是线段AB、CD中点,求EF。
课外巩固
1. .如果点C在AB上,下列表达式①AC=AB;②AB=2BC;③AC=BC;④AC+BC=AB中, 能表示C是AB中点的有( )
A.1个 B.2个 C.3个 D.4个
2.如图,从A到B有3条路径,最短的路径是③,理由是( )
A.因为③是直的 B.两点确定一条直线
C.两点间距离的定义 D.两点之间,线段最短
3. 如图,点B、C在线段AD上,则
AC =_______+______ = ______—______,
BC =______—______ = ______—______。
4..已知A,B,C为直线l上的三点,线段AB=9cm,BC=1cm,那A,C两点间的距离是
5. 长为12cm的线段AB上有一点P,M,N分别为PA,PB的中点,则线段MN= ______
6. 量出线段的长度,并比较:
(1)AB=_________cm;AC=_________cm;
AD=_________cm;AE=_________cm。
(2)比较线段的长度。
7. 试用叠合法比较线段:
8. 右图中,线段AB长为24cm,若AD长是CD长的一半少6cm,BC是CD的长的一半多1cm,求线段CD的长度。
4.3.1角
第一课时
名师归纳与点拨
知识点1 角的定义:
静态定义:有公共端点的两条射线组成的图形叫做角,这个公共端点是角的顶点,这两条射线是角的两条边.
说明:公共端点A叫做该角的顶点, 射线AB、AC叫做该角的两条边,
角的符号:∠
动态定义:角也可以看作是一条射线绕着它的端点旋转而形成的图形。
知识点2 角的表示方法:
①用三个字母∠AOB或∠BOA 或用角的顶点∠O②用希腊字母记作∠α③用小写的数字记作∠1
说明:用单个大写字母表示,顶点处只能有一个角
例1.判断下列哪些图形是角
① ② ③ ④
思路导引 根据角的静态定义:“有公共端点的两条射线组成的图形叫做角,这个公共端点是角的顶点,这两条射线是角的两条边”.
解:①③④
例2.如图,(1)图中共有几个角?请把它们表示出来.
(2)能把∠AOB记作∠O吗 为什么 ∠AOB还可以怎样表示呢?
思路导引 一个顶点处不止一个角时,就不能用一个大写字母表示角。
解:(1)图中共有三个角,分别是:∠AOB、∠AOC、∠BOC
(2)不能,因为“一个顶点处不止一个角时,就不能用一个
大写字母表示角”,∠AOB还可以表示为∠BOA.
课内达标
1. 下列语句正确的是( )
A.两条直线相交,组成的图形叫做角
B.两条有公共端点的线段组成的图形叫角
C.两条有公共点的射线组成的图形叫角
D.从同一点引出的两条射线组成的图形叫角
2.用三个大写字母表示角:
∠1为 ;∠ 2为 ;
∠3为 .; 可以用一个大写字母表示的角是______
3. 图中以OC为边的角有______个,它们分别是______
4.以O为顶点的角有几个,请分别把他们写出来。
课外巩固
1. 下列四个图形中,能用∠1,∠AOB,∠O三种方法表示同一个角的是 ( )
2.如图,图中共有( )个角.
(A) 6 (B)7 (C)8 (D)9
3.如下左图所示,把图中用数字表示的角,改用大写字母表示分别是________.
4.将上右图中的角用不同的方法表示出来,填入下表:
∠1 ∠3 ∠4
∠BCA ∠ABC
5.用三个字母表示图中所注的∠1、∠2、∠3:
(1) (2) (3)
∠1是______; ∠1是______; ∠1是______;
∠2是______; ∠2是______; ∠2是______;
∠3是______; ∠3是______; ∠3是______;
∠4是______.。
6如图,图中能用一个大写字母表示的角有几个 分别把它们表示出来.
7.如图,(1)中有几个角?(2)中有几个角;(3)中有几个角.以此类推,若从一点o引n条射线,则以点0为顶点的角【最大的角都小于平角】有几个?
8.想一想,做一做.
(1)用字母表示图中的每个城市.
(2)请用字母在下图分别表示以北京为中心的每两个城市之间的夹角.
( http: / / www. / )
4.3.1角
第二课时
名师归纳与点拨
知识点1 角的度量方法:
计量角的大小常用的单位是“度”,用符号“°”表示。把半圆平均分成180份,每一份所对的角叫做1度的角,记作1°。使用量角器的方法:把量角器放在角的上面,使量角器的中心和角的顶点重合,零度刻度线和角的一条边重合,角的另一条边所对的量角器上的刻度,就是这个角的度数
说明:度量角的工具:一般用量角器
知识点2 以度、分、秒为单位的角度制规定,
把一个周角_等分为360份_____,每一份叫做1度,记作___1°___;把1度的角__等分为60份____,每一份叫做1分,记作___1′___;把1分的角__等分为60份____,每一份叫做1秒,记作___1″___.这样,1周角是_360____°,1平角是__180____°,1°=__60____',1′=___60___″.
例1:时钟在5点15分时,时钟的时针与分针所成的角是多少度?
思路导引 根据钟面上时针走一圈(360°)需要12小时=12*60=720分钟,即时针的速度是360/720=0.5°/分钟;分针走一圈(360°)需要1小时=60分钟,即时针的速度是360/60=6°/分钟.即时针走过一小时在钟面上扫过30°,分针在钟面上走过一分钟扫过6°。
解:所以时针离开12点的角度为5*30°+15*0.5°=157.5°,
分针离开数字12的角度为15*6°=90°,
157.5°-90°=67.5°。
所以5点15分时,时钟的时针和分针所成的锐角是67.5°。
课内达标
1. 在钟表上,1点30分时,时针与分针所成的角是( ).
A.150° B.165° C.135° D.120°
2.如图,量出图中三个角的度数分别是__________,这三个角的和是_____.
3.如图所示,点O在直线AB上,图中小于180°的角共有 个
4.如下图,分别确定四个城市相应钟表上时针与分针所成角的度数.
课外巩固
1. 下列各角中,不可能是钝角的角是( ).
A.周角 B.平角 C.钝角 D.直角.
2. 下列说法正确的是( )
(A)一个周角就是一条射线 (B)平角是一条直线
(C)角的两边越长,角就越大 (D)∠AOB也可以表示为∠BOA
3.用一副三角板可以拼出________的角.
4. 30.6°=_____°_____′=_______′
5. 时钟从3点15分走到3点35分,它的分针转过________度.
6.计算:
(1)53°28′+47°32′; (2)17°50′-3°27′;
7.已知:如图,AOB是直线,∠1∶∠2∶∠3=1∶3∶2,求∠DOB的度数.
8. 小明先在笔直的路AB上行走,走道B点后拐了个弯,然后在笔直的路BC上行走,走到C点后, 又拐了个与刚才相同角度的弯.请画出拐弯后的行走路线
4.3.2角的比较与运算
名师归纳与点拨
知识点1 角的大小比较的两种方法:
一种方法为度量法:可以用量角器量出角的度数,然后比较它们的大小,另一种方法为叠合法:即把他们叠合在一起比较大小。
说明:1.在用叠合法比较两角大小时,顶点必须重合,一边必须重合,另一边落在其余一边的圆旁。2.角的大小只与角两边的张大张小有关,而与角的边画出部分长短无关。3.角的和、差、倍、分的度数,等于它们度数的和、差、倍、分。
知识点2 把一个角分成相等的两个角的射线叫做这个角的平分线,类似的还有角的三等分线等。
说明:角平分线的画法一般有两种
(1)借助量角器画图:以已知角顶点为顶点,已知角的一边为边,在已知线的内部画一个度数等于已知角度数一半的角,则这个角的另一边就是已知角的平分线.
(2)用折叠方法:把角沿顶点对折,使角的两边重合,沿折痕在角的内部画一条射线即为已知角的平分线.
说明:角平分线也是一条射线,角平分线在角的内部,角平分线分成的两个角度数相等。
例1.已知O为直线AB上一点,∠AOC的平分线OM,∠BOC的平分线为ON,求∠MON的度数?
思路导引 根据平角的定义可知∠AOB=180°,再根据OM平分∠AOC,则2∠MOC=∠AOC,同理可得2∠NOC=∠BOC,而
∠AOC+∠BOC=180°,所以2∠MOC+2∠NOC=180°,
∠MOC+∠NOC=90°
解: ∠MON的度数为90°.
课内达标
如图,射线OD是平角∠AOB的平分线,∠COE=90°,那么下列式子中错误的是( ).
(A)∠AOC=∠DOE (B)∠COD=∠BOE
(C)∠AOD=∠BOD (D)∠BOE=∠AOC
2.如图,∠AOB∠COD,则∠1 ∠2(填“<,>, =”)
3.如图,用“=”或“>”或“<”填空:
(1)∠AOC_______∠AOB+∠BOC; (2)∠AOC_______∠AOB;
(3)∠BOD-∠BOC______∠DOC;
4. 如图,已知:∠BOC=2∠AOB,OD平分∠AOC,∠BOD=140求:∠AOB的度数。
课外巩固
1. 射线OC在∠AOB的内部,下列四个式子中不能判定OC是∠AOB的平分线的是( ).
(A)∠AOB=2∠AOC (B)∠BOC=∠AOC
(C)∠AOC∠AOB (D)∠AOC+∠BOC=∠AOB
2. .如图,OC是∠AOB的平分线,OD平分∠AOC,且∠COD=25°,则∠AOB=( ).
(A)100° (B)75°
(C)50° (D)20°
3. 如图,OM是∠AOB的平分线且∠AOM=30°,
则∠BOM=______;∠AOB=______.
4.如图,在横线上填上适当的角:
(1)∠AOC=______+______;
(2)∠AOD-∠BOD=______;
(3)∠BOC=______-∠COD;
(4)∠BOC=∠AOC+______-______.
5.按图填空:
(1)∠ABC是∠ABD与∠DBC的______;
(2)∠BDC是∠ADC与∠ADB的_______.
6. 下面是小马虎解的一道题.
题目:在同一平面上,若∠BOA=70°,∠BOC=15°,求∠AOC的度数.
解:根据题意可画出下图.
∵∠AOC=∠BOA-∠BOC
=70°-15°
=55°,
∴∠AOC=55°.
若你是老师,会给小马虎满分吗 若会,说明理由.若不会,请将小马虎的错误指出,并给出你认为正确的解法.
7. 如图,OD、OE分别是∠AOC和∠BOC的平分线,∠AOD=40°,∠BOE=25°,求∠AOB的度数.
解:∵OD平分∠AOC,OE平分∠BOC,
∴∠AOC=2∠AOD,
∠BOC=2∠______.
∵∠AOD=40°,∠BOE=25°,
∴∠BOC=______,
∠AOC=______.
∴∠AOB=____.
8. 如图,∠AOB的平分线为OM,ON为∠MOA内的一条射线,OG为∠AOB外的一条射线,某同学经过认真的分析,得出一个关系式是∠MON=(∠BON-∠AON),你认为这个同学得出的关系式是正确的吗 若正确,请把得出这个结论的过程写出来。
4.3.3 余角与补角
第一课时
名师归纳与点拨
知识点1余角与补角的定义
如果两个角的和等于90°(直角),就说这两个角互为余角,即其中一个角是另一个角的余角;如果两个角的和等于180°(平角),就说这两个角互为补角,即其中一个角是另一个角的补角.
说明:互余互补是两个角之间的关系,且互为余角是两角之和等于90°(直角),互为补角是两角之和等于180°(平角).“互为”一词的意思,于是得到: 互余、互补的角总是成对出现的.
知识点2余角与补角的性质
①等角的余角相等②等角的补角相等
说明:等(或同)角的余(或补)角相等”这一性质在今后的角度转换中经常用到,应引起重视.
例1:如图,直线AB与CD相交于一点,那么∠1=∠2吗?试说明理由.
思路导引:∵直线AB与CD相交于一点O(已知)
∴∠1与∠3互为补角,∠2与∠3互为补角(互为补角的定义)∴∠1=∠2(等角的补角相等)
解:∠1=∠2
例2:如图,∠AOB是直角,∠COD=90°,OB平分∠DOE,则∠3与∠4是什么关系?并说明理由.
思路导引:∵∠AOB是直角,∠COD=90°(已知)
∴∠1+∠2=90°,∠1+∠3=90°(互为余角的定义)
∴∠2=∠3(等角的余角相等)
∵OB平分∠DOE(已知)
∴∠2=∠4(角平分线的定义)
∴∠3=∠4(等量代换)
解:∠3=∠4
课内达标:
1.已知:如图,∠AOB=∠COD=90°,则∠1与∠2的关系是 ).
(A)互余 (B)互补
(C)相等 (D)无法确定
2.若一个角的余角和它的补角互补,那么这个角为______度。
3.一个角的4倍和这个角的余角互补,这个角是______度。
4. 如图,∠AOC=∠BOD=90 ,∠AOD=130 ,求∠BOC的度数。
课外巩固
1. 互为余角的两个角之差为35°,则较大角的补角是( )
A.117.5° B.112.5° C.125° D.127.5°
2、正确的有( )
⑴一个角的补角一定是钝角,⑵互补的两个角不可能相等,(3)∠A的补角与∠A的余角的差一定等于直角(4)两个锐角一定互为余角,(5)直角没有补角,(6)如果∠MON=180 ,那么M、O、N三点在一条直线上。
A、1个;B、2个;C、3个;D、4个
3. 若∠ 与∠ 互补,∠ 与∠ 互余,则∠ 与∠ 的差为____________.
4.如图,已知A,O,E三点在同一条直线上,OB平分∠AOC,OD平分∠COE,则∠BOC与∠COD的关系为____________.
5. 如图,∠ACB=∠CDB=90 ,图中∠ACD的余角有 个。
6.填写下列空白和理由 ,如右图,
∵∠AOB+∠BOC+∠COD+∠DOA=1周角,
∴∠AOB+∠BOC+∠COD+∠DOA=360°.
(理由_____________________.)
∵∠AOB=∠COD=90°,
∴∠AOD+∠BOC=180°.
(理由:__________________)
又∵∠BOC=42°,
∴∠AOD=180°-∠BOC=180°-42°=__________.
7. 如图所示,∠AOC=90°,OB⊥OD,则与∠BOC相等的角有谁?图中共有多少对互为余角请写出来。
8.如图,O是直线AB上的一点,OM是∠AOC的角平分线,ON是∠BOC的角平分线,
(1)图中互余的角有几对?请写出来。
(2)图中互补的角有几对?请写出来。
4.3.3 余角与补角
第二课时
名师归纳与点拨
知识点1用角度表示方向:一般以正北、正南为基准,用向东或向西旋
转的角度表示方向,如图所示,OA方向可表示为北偏西60 。
说明:(1)用量角器画这样的射线OA时要注意:(1)是以正南或者是正北方向
做角的始边,(2)要理解偏东,偏西的意义。
(3)正北,正南,正西,正东,射线OD OC OB OA
西北方向:射线OE;西南方向:射线OF东南方向:射线OG;东北方向:射线OH
直线AB和直线CD互相垂直,所成四个角均为直角
知识点2 如何表示乙地对甲地的方位角
1. 先找出中心点,然后画出方向指标
2. 把中心点和目的地用线连接起來
3.度量向北的射线和视线之间的角度
例1. 如图,A地和B地都是海上观测站,从A地发现它的北偏东50°方向上有一艘船,同时从B地发现这 艘船在它的北偏东30°方向,试在图中确定这艘船的位置。
思路导引:找到A地北偏东50°和B地北偏东30°的射线。两条射线的交点即为这艘轮船的位置。
解:
课内达标
1.轮船航行到C处测得小岛A的方向为北偏西32°,那么从A观测此时的C处的方向为( ).
(A)南偏东32° (B)东偏南32°
(C)南偏东68° (D)东偏南68°
2.若轮船甲自A岛沿北偏东45°的方向行驶30海里到达B岛,轮船乙自A岛沿南偏西
70°的方向行驶50海里到达C岛,则∠BAC=____________.
3. 如图,由A到B的方向是 ____________
4..在图中画出表示下列方向的射线:
(1)南偏西30° (2)南偏东25°
(3)北偏西20° (4)北偏东65°
(5)东北方向 (6)西南方向
课外巩固
1.A看B的方向是北偏东21°,那么B看A的方向( )
A:南偏东69° B:南偏西69° C:南偏东21° D:南偏西21°
2.如图,下列说法中错误的是( )
A: OC的方向是北偏东60°
B: OD的方向是南偏东60°
C: OB的方向是西南方向
D: OA的方向是北偏西22°
3.在点O 北偏西60°的某处有一点A,在点O南偏西20°的某处有一点B,则∠AOB的度数是_____
4.如图,甲从A点出发向北偏东70°方向走50m至点B,
乙从A出发向南偏西15°方向走80m至点C,则∠BAC的度数是_____
5.说出B在A的____,那么A在B的______.
6.如图,分别指出A,B,C,D在O的什么方向
7. 如图所示,A、B两条海上巡逻艇同时发现海面上有一不明物体,A艇发现该不明物体在它的东北方向,B艇发现该不明物体在它的南偏东60°的方向上, 请你试着在图中确定这个不明物体的位置.
8.小明从点A出发向北偏西50°方向走了3米,到达点B,小林从点A出发向南偏西40°方向走了4米,试画图确定出A、B、C三点的位置(用1厘米表示3米),并从图上求出B点到C点的实际距离
章末总结复习
知识体系构建
知识:(一)多姿多彩的图形
立体图形:棱柱、棱锥、圆柱、圆锥、球等。
1、几何图形
平面图形:三角形、四边形、圆等。
主(正)视图---------从正面看
2、几何体的三视图 侧(左、右)视图-----从左(右)边看
俯视图---------------从上面看
3、点、线、面、体
(1)几何图形的组成
点:线和线相交的地方是点,它是几何图形最基本的图形。
线:面和面相交的地方是线,分为直线和曲线。
面:包围着体的是面,分为平面和曲面。
体:几何体也简称体。
(2)点动成线,线动成面,面动成体
(二)直线、射线、线段
1、基本概念
直线 射线 线段
图形
端点个数 无 一个 两个
表示法 直线a直线AB(BA) 射线AB 线段a线段AB(BA)
作法叙述 作直线AB;作直线a 作射线AB 作线段a;作线段AB;连接AB
延长叙述 不能延长 反向延长射线AB 延长线段AB;反向延长线段BA
2、直线的性质
经过两点有一条直线,并且只有一条直线。
简单地:两点确定一条直线。
3、线段的中点(二等分点)、三等分点、四等分点等
定义:把一条线段平均分成两条相等线段的点。
图形:
A M B
符号:若点M是线段AB的中点,则AM=BM=AB,AB=2AM=2BM。
4、线段的性质
两点的所有连线中,线段最短。简单地:两点之间,线段最短。
5、两点的距离
连接两点的线段长度叫做两点的距离。
6、点与直线的位置关系
(1)点在直线上 (2)点在直线外。
(三)角
1、角:由公共端点的两条射线所组成的图形叫做角。
2、角的表示法(四种):
3、角的度量单位及换算
4、角的分类
∠β 锐角 直角 钝角 平角 周角
范围 0<∠β<90° ∠β=90° 90°<∠β<180° ∠β=180° ∠β=360°
5、角的和、差、倍、分及其近似值
6、角的平线线
定义:从一个角的顶点出发,把这个角分成相等的两个角的射线叫做角的平分线。
7、互余、互补
(1)若∠1+∠2=90°,则∠1与∠2互为余角。其中∠1是∠2的余角,∠2是∠1的余角。
(2)若∠1+∠2=180°,则∠1与∠2互为补角。其中∠1是∠2的补角,∠2是∠1的补角。
(3)余(补)角的性质:等角的补(余)角相等。
8、方向角
(1)正方向
(2)北(南)偏东(西)方向
能力:1.能判断简单物体(直棱柱、圆柱、圆锥、球)的三视图。
2.能根据三视图描述基本几何体或实物原型。
3.能根据展开图判断立体模型。
4.能借助量角器能画出给定度数的角。
5.能正确的分辨并表示方位角
方法:1. 用“度量法”和“用尺规作图法”画一条线段等于已知线段,并用“度量法”和“叠合法”比较线段的大小
2. 用“度量法”和“叠合法”比较角的大小
3.借助三角尺能画出15°的倍数的角,在0~180°之间共能画出11个角。
4.用尺规作图法画出一个角与已知角相等
综合题型剖析
已知如图,线段AD=6,线段AC=BD=4,E,F分别是线段AB,CD的中点,求EF。
思维导引 因为AC=BD=4,所以
可得AC+BC+BC+CD=8,又知道AB+BC+CD=6,所以可以求得BC=8-6=2,因此也可推出AB=2,CD=2,又根据E,F分别是AB,CD的中点可知,EB=1,CF=1,因此可求得EF.
解:
点拨:此题关键是由AC+BD=8cm,把线段分解以后气的BC的长。
例2. 若∠AOB=∠COD=∠AOD,已知∠COB=80°,求∠AOB、∠AOD的度数
思路导引 因为已知∠AOB=∠COD=∠AOD,所以可设∠AOB=x°,则可推出∠COD=x°,∠AOD=6 x°,有根据图可以知道∠AOD=∠AOB+∠COB+∠COD,因此可以推出∠COB=4 x°,又告诉了∠COB=80°,所以可求出图中所有角的度数。
解:
点拨: 根据条件推导出∠COB=4 x°=80°是本题的关键所在。
例3.如图所示,学校、工厂、电视塔在平面图上的标点分别是A、B、C,工厂在学校的北偏西30°电视塔在学校的南偏东15°,则平面图上的∠BAC应是多少度?
思路导引 这是关于方位角的问题,现在要求∠BAC的度数,首先应明白∠BAC是由∠BAD和∠CAD组成的,然后根据条件即可解出∠BAC的度数。
解:
点拨: 解此题时一定要搞清方位角的大小。
综合练习巩固
选择题
1.在以下四个图形中,经过折叠能围成一个正方体的是( )
2.如图,能用∠1,∠ACB,∠C三种方法表示同一个角的是 ( )
3. ①平角是一条直线;②射线是直线的一半;③射线AB与射线BA表示同一条射线;④用一个扩大2倍的放大镜去看一个角,这个角会扩大2倍;⑤两点之间,线段最短;⑥120.5°= 120°50 .
以上说法正确的有( )
A .0个 B.1个 C.2个 D.3个
二.填空题
4.已知中,,,的平分线交于点,则的度
数为
5.已知互余两角的差为,则这两个角的度数分别为
6. 如图,AB=16 cm,C是AB上一点,且AC=10 cm,D是AC的中点,E是BC的中点,则线段DE的长度为
三,解答题
7. 如图所示,∠AOC=90°,OB⊥OD,则与∠BOC相等的角有谁?图中共有多少对互为余角请写出来。
8. 如图,OA的方向是北偏东15°,OB的方向是西偏北50°。
(1)若∠AOC=∠AOB,则OC的方向(方位角)是____
(2)OD是OB的反向延长线,OD的方向是(方位角)是_________;
(3)∠BOD可看作是OB绕点O逆时针方向至OD,
作∠BOD的平分线OE,并用方位角表示OE的方向。
(4)在(1)、(2)、(3)的条件下,求∠COE。
学业水平测试
1. .(2010·滨州中考)
2. (2008·十堰中考)如图,C、D是线段AB上两点,若CB=4cm,DB=7cm,且D是AC的中点,则AC的长等于( )
A.3cm B.6cm C.11cm D.14cm
3.(2010·凉山中考)将一副三角板按图中的方式叠放,则角等于( )
A. B. C. D.
4. .(2009·长沙中考)如图,于点是的平分线,则的度数为 .
5.(2009·云南中考)如图,点C是线段AB上的点,点D是线段BC的中点,若AB=10,AC=6 ,则CD=_______________.
( http: / / )
6.(2009·枣庄中考)如图,将一副三角板叠放在一起,使直角顶点重合于O点,则 .
7. (2010湖南娄底)如图6,直线AB、CD相交于点O,OE平分∠AOD,若∠BOD=100°,求∠AOE的度数。
8. (2009山东枣庄)如图,将一副三角板叠放在一起,使直角顶点
重合于O点,求的度数。
9.(2010 嵊州市)如图,平面内有公共端点的六条射线OA,OB,OC,OD,OE,OF,从射线OA开始按逆时针方向依次在射线上写出数字1,2,3,4,5,6,7,….
(1)“17”在射线 上.)
(2)请任意写出三条射线上数字的排列规律.
(3)“2007”在哪条射线上?
10.(2010年杭州市)已知直四棱柱的底面是边长为a的正方形, 高为, 体积为V, 表面积等于S.
(1) 当a = 2, h = 3时,分别求V和S;
(2) 当V = 12,S = 32时,求 ( http: / / www. / )的值.
学业水平考试卷
(时间60分钟,满分100分)
班级 姓名 得分
一.选择题(每小题3分,共24分)
下图所示几何体的俯视图是( )
A B C D
2、下列图形中为正方体的平面展开图的是 ( )
A B C D
3.如图7,∠AOE=∠BOC,OD平分∠COE,
那么图中,相等的角共有( )
A.1对 B.2对
C.3对 D.4对 <图7>
4. 如图,能用∠1,∠ACB,∠C三种方法表示同一个角的是 ( )
5. ①平角是一条直线;②射线是直线的一半;③射线AB与射线BA表示同一条射线;④用一个扩大2倍的放大镜去看一个角,这个角会扩大2倍;⑤两点之间,线段最短;⑥120.5°= 120°50 .
以上说法正确的有( )
A .0个 B.1个 C.2个 D.3个
6.如图,AB=16 cm,C是AB上一点,且AC=10 cm,D是AC的中点,E是BC的中点,则线段DE的长度为 ( )
A.6 cm B.8 cm C.10 cm D.12cm
7.如图10,由A到B的方向是( )
A.南偏东30° B.南偏东60°
C.北偏西30° D.北偏西60°
8.如图所示,从O点出发的五条射线,可以组成角的个数是( ).
A.10个 B.9个 C.8个 D.4个
二.填空(每小题3分,共24分)
9.圆柱的侧面展开图是一个 ,圆锥的侧面展开图是一个 ,棱柱的侧面展开图是一个 。
10.北京时间2点30分,钟面上的时针和分针的夹角为 度。
11.如图1,已知CB=5,DB=7.5,D是AC的中点,
则AC=_________ . <图1>
12.126.31°=____°____′___″
13.如图2,CB⊥AB,∠CBA与∠CBD的度数比是4:1,则∠DBA=________度,
∠CBD的补角是_________度.
<图2> <图3>
14.如图3,AC⊥BC,CD⊥AB,点A到BC边的距离是线段_____的长,点B到CD边的距离是线段_____的长,图中的直角有_____________,∠A的余角有_______________,和∠A相等的角有__________.
15. 如图,折叠围成一个正方体时,数字 会在与数字2所在的平面相对的平面上。
16. 如图是由一些相同的小正方体构成的几何体的三视图,这些相同的小正方体的个数是
。
三.解答题
17.作图:(1)(5分)如图,有一个几何体,请画出看它的三视图
18.(5分)已知线段a、b(如图),画出线段AB,设AB=3a-b,并写出画法.
19.计算(每小题2分,共8分)
①.37°28′+44°49′; ②.108°18′-52°30″;
③.25°36′×4; ④ .40°40′÷3.
20.(7分)一个角的余角的两倍比它的补角的 少40°,求这个角的度数.
21. (7分)如图,已知直线和相交于点,是直角,平分,,求的度数.
22.(10分)如图,M是线段AB的中点,点C在线段AB上,且AC=4 cm,N是AC的中点,
MN=3 cm,求线段CM和AB的长
23.(10分)如图,∠AOB是直角,∠AOC等于46°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数.
附加题
已知∠ 与∠ 互为补角,且∠ 互为补角,且∠ 的比∠ 大15°,求∠ 的余角.
4.1.1 几何图形
课内达标
1.D 2,长方形 3.球,正方体4.立体图形:①④⑤⑥⑦;平面图形:②③
课外巩固
1.C 2.A 3. (1) 正方体 (2)长方体 (3) 三棱柱(4)四棱锥 (5)圆柱 4.7,9
5.正方体,球 6. 分析:主视图有2列,第一列3个小正方形,第2列有1个小正方形;左视图有3列,小正方形数目分别为1,3,2;俯视图有3行,小正方形数目分别为1,2,1.
解: 如图:
7.x=1 8.
4.1.2 几何图形
课内达标
B 2. 点动成_线_____;线动成__面____;面动成___体____ 3.点动成线
4.
课外巩固
1. B 2.D 3.一,曲 4.面动成体 5.
6. 思路解析:分类时一定要注意把握好特征,做到不重不漏,标准统一.
答案:(1)柱体:①,③,④,⑤,⑦;锥体:②;球体:⑥
(2)组成的面有曲面:②,⑥,⑦;组成的面是平面:①,③,④,⑤
7. 思路解析:线段旋转一周形成一个圆,长方形旋转一周形成一个圆柱,半圆旋转一周会形成球 答案:(1)与C;(2)与A;(3)与B连起来.A是圆台;B是球;C是圆柱与圆锥的组合.
8.
4.2.1直线、线段、射线
第一课时
课内达标
1. B 2.2,经过两点有且只有一条直线 3. .AB CD O CD EF 4. (1)4 1 (2)6 3 (3)8 6 (4)2n n(n-1)
课外巩固
1.C 2.A 3.上,外 4.2,射线AB,射线BA 5.OE 6.直线AB与直线CD交于点O,点E在直线l上 7. 道理:经过两点,有且只有一条直线 8. (1)4,7(2)11
4.2.2直线、线段、射线
第二课时
课内达标
1.D 2.(2),两点之间,线段最短 3.3, 4.
课外巩固
1.C 2.D 3.AB+BC=AD-CD;AC-AB=BD-CD 4. 5.6cm
6.略 7.略 8.14.5cm
4.3.1角
第一课时
课内达标
1.D 2. ∠EDB, ∠DBE, ∠ABC: ∠A, ∠C, ∠D 3.3, ∠DOC, ∠COB, ∠COA
4. .以O为顶点的角有几个,请分别把他们写出来。
解:共有10个角,
分别是:
∠AOB,∠AOC,
∠AOD,∠AOE,
∠BOC,∠BOD,
∠BOE,∠COD,
∠COE,∠DOE。
课外巩固
1.B 2.A 3. ∠ADE, ∠DEC
4.
5.(1) ∠AGB, ∠ACE, ∠DEC(2) ∠EGB, ∠EHB, ∠CHG(3) ∠DAC, ∠ACB, ∠BAC, ∠ACD
6.3个,∠A,∠B,∠C 7.3,6,10, 8.略
4.3.1角
第二课时
课内达标
1.C 2,略 ,180° 3.9 4. 30°,0°,120°,90°
课外巩固
1.D 2.D 3.75°、105°、135°、120°、15°、30°、150°、180°
4.30,36,216 5.10 6. (1)101° (2)14°23′ 7.30° 8.略
4.3.2角的比较与运算
课内达标
1.D 2.= 3.=,>,= 4.28°
课外巩固
1.D 2.A 3.30°,60°4.
5.和,差 6.55°或者是85°,分OC在角内部及角外部两种情况讨论
7. 解:∵OD平分∠AOC,OE平分∠BOC,
∴∠AOC=2∠AOD,
∠BOC=2∠_ BOE _____.
∵∠AOD=40°,∠BOE=25°,
∴∠BOC=__50°____,
∠AOC=__80°____.
∴∠AOB=__130°__.
8.∠BON=∠BOM+∠MON=1/2∠AOB+∠MON
∠AON=∠BOM-∠MON=1/2∠AOB-∠MON
∠BON-∠AON=(1/2∠AOB+∠MON)-(1/2∠AOB-∠MON)=2∠MON
∠MON=1/2(∠BON-∠AON)
4.3.3 余角与补角
第一课时
课内达标
1.B 2.45° 3.30° 4.50°
课外巩固
1.A 2.B 3.90° 4.互余 5.2个 6.周角的定义,等式基本性质1,138 °
7.
8.。有四对互余的角∠AOM与∠CON,∠AOM与∠BON,
∠COM与∠CON,∠COM与∠BON,3对互补的角:∠BON与∠NOA,∠BOC与∠AOC, ∠BOM 与∠AOM
4.3.3 余角与补角
第二课时
课内达标
1.A 2.155° 3.北偏西60° 4.略
课外巩固
1.C 2.A 3.110° 4.125° 5.北偏西40度,南偏西40度
6.A在O的北偏东60度,B在O的北偏西30度,C在O 的南偏西75度,D在O的西南方向
7.如图
综合练习巩固
1.B 2.C 3.B 4.120° 5.55°或者是35° 6.8cm 7.略 8.北偏东70°,南偏东40°,南偏西40度,北偏东40°,160°
学业水平测试
1.B 2.B 3.A 4.135° 5.2 6.180° 7.40° 8.180°
9. 【解析】(1)“17”在射线上.
(2)射线上数字的排列规律:
射线上数字的排列规律:
射线上数字的排列规律:
射线上数字的排列规律:
射线上数字的排列规律:
射线上数字的排列规律:
(3)在六条射线上的数字规律中,只有有整数解.解为
“2007”在射线上.
10. 答案:
(1) 当a = 2, h = 3时,
V = a2h= 12 ;
S = 2a2+ 4ah =32 .
(2) ∵a2h= 12, 2a(a + 2h) =32,
∴ , (a + 2h) =,
∴===.
学业水平考试卷
1.C 2.C 3.B 4.C 5.B 6.B 7.B 8.10 9.长方形,扇形,长方形 10.105°
11.5 12. ___126_°_18___′__36_″ 13.72°,162° 14.AC, BD, ∠AOC, ∠COD,
∠ACB, ∠ACD, ∠B, ∠DCB 15.5 16.5 17.略
18. 【答案】
方法一:
①量得a=1.9 cm,b=2.6 cm;
②算AB的长,AB=3×1.9-×2.6=4.4(cm);
③画线段AB=4.4 cm.
则线段AB就是所要画的线段.
方法二:
①画射线AM,并在射线AM上顺次截取AC=CD=DE=a;
②在线段EA上截取EB=b.
则线段AB就是要画的线段.
19. 【提示】
1°=60′,1′=60″,低一级单位满“60”,要向高一级单位进“1”,由高一级单位借“1”要化成“60”加入低一级单位参与运算.
【答案】1.82°17′; 2.56°17′30″; 3.102°24′; 4.13°33′20″.
20.40° 21.24°
22. 【提示】CM=MN-NC,AB=2 AM.
【答案】∵ N是AC中点,AC=4 cm,
∴ NC=AC=×4=2(cm),
∵ MN=3 cm,
∴ CM=MN-NC=3-2=1(cm),
∴ AM=AC+CM=4+1=5(cm),
∵ M是AB的中点,
∴ AB=2 AM=2×5=10(cm).
答:线段CM的长为1 cm,AB的长为10 cm.
23. 【提示】
∠MON=∠CON-∠COM.
【答案】
∵ ∠AOB是直角.
∴ ∠AOB=90°(直角的定义),
∵ ∠AOC=46°,
∴ ∠BOC=∠AOB+∠AOC=90°+46°=136°,
∵ ON平分∠BOC,
∴ ∠CON=∠BOC=×136°=68°(角平分线定义),
∵ OM平分∠AOC,
∴ ∠COM=∠AOC=×46°=23°(角平分线定义),
∴ ∠MON=∠CON-∠COM=68°-23°=45°.
答:∠MON=45°.
【点评】
和线段计算一样,在进行有关角度计算时,也要根据已知,仔细看图,找出已知角与所求角的关系,此题中的∠MON还可看成是∠BOM与∠BON的差,∠MON也可看成是∠AOM与∠AON之和,请试一试怎么算,比一比哪种方法较简便.关于角平分线的三种表达式,也应结合图形灵活运用.
附加题:【提示】
互补两角和为180°,根据题意可知列出关于∠ 、∠ 的方程组,求出∠ ,再根据“互余两角和为90°”,求出∠ 的余角.
【答案】
由题意可得:
解之得:
∴ ∠ 的余角=90°-∠ =90°-63°=27°.
答:∠ 的余角是27°.
图4-1-1
A.
B.
C.
D.
建
设
和
谐
昆明
明
图4-1-2
正面
左面
上面
-2
A
x
3
1
3x-2
点
线
面点
体点
动
交
交
交
动
动
③
①
②
C
A
B
O
O
A
C
D
E
A
B
C
O
A
B
D
C
3
1
2
4
A
C
D
B
C
A
D
B
E
3
1
2
4
60
B
C
D
A
A
E
B
C
F
D
O
D
C
B
A
东
D
B
C
A
北
西
南
A.
B.
C.
D.
( )
A
C
B
D
E
O
图6
A
B
C
D
O
1
(第3题图)
A
B
C
D
E
O
名师归纳与点拨
知识点1 几何图形可分为平面图形和立体图形
平面图形的定义:各部分都在同一平面的图形。
立体图形的定义:具有长、宽、高的物体。
说明:长方形、正方形、三角形、圆等都是我们十分熟悉的平面图形;长方体、正方体、球、圆柱、圆锥等都是立体图形.
知识点2 立体图形和平面图形的转化
一个立体图形从不同方向看,可以是一个平面图形;可以把立体图形进行适当的裁剪,把它展开成平面图形,或者把一个平面图形复原成立体图形,即立体图形与平面图形可以互相转换.
说明: ①在画三视图时一般要求“长对正,高平齐,宽相等”。②不是所有的立体图形都可以展开,例如球体便不可以展开。
例1:下列几种图形:①长方形;②梯形;③正方体;④圆柱;⑤圆锥;.其中属于立体图形的是( )
A. ①②③;B. ③④⑤;C. ③⑤;D.④⑤
思路导引 根据几何图形的各部分不都在同一平面内,具有长、宽、高,那么此几何图形就是一个立体图形来进行判断。
解:选B
例2:如图4-1-1,表示一个用于防震的形的包装用泡沫塑料,当从上面看这一物体时看到的图形形状是( )
思路导引 从上往下看此物体得到的是它的俯视图,注意“看得见的轮廓线用实线,看不见的轮廓线用虚线”。
解:选B
课内达标
1. 一个正方体的平面展开图如图所示,将它折成正方体后“建”字对面是( )
A.和 B.谐
C.昆 D.明
2. 圆柱的侧面展开图是_______形。
3.主视图、左视图、俯视图都一样的几何体为________
4. 下图中哪些图形是立体的,哪些是平面的
课外巩固
1. 下图中,不是左图所示物体视图的是( )
2.若下图是某几何体的三种不同方向的视图,则这个几何体是( )
A.圆柱 B.正方体
C.球 D.圆锥
3.分别写出表面能展开成如图所示的五种平面图的几何体的名称.
(1)_______ (2)_______ (3)_______ (4)_______ (5)_______
4. 若一个棱柱的底面是一个七边形,则它的侧面必须有 个长方形,它一共
有 个面。
5. 观察一个几何体,上看下看、左看右看、前看后看,看到的都是一个同样大小的正方形,这个几何体是 ,如果看到的都是一个同样大小的圆,则该几何体是
6. .画出图中的七块小立方块组成的几何体的主视图、左视图和俯视图.
7.如图是一个正方体的展开图,标注了字母A的面是正方体的正面,设正方体的左面与右面所标注的代数式的值相等,求x的值。
8. 如图,沿长方形纸片上的边线剪下的阴影部分,恰好能围成一圆柱,设圆半径为r
(1)用含r的代数式表示圆柱的体积; 中间的四边形是正方形
(2)当r=3,圆周率取3.14时,求圆柱的体积(保留整数)。
4.1.2 几何图形
名师归纳与点拨
知识点1 点、线、面、体组成几何图形,点是构成图形的基本元素。
包围着体的是面,面与面相交的地方时线,线与线相交的地方是点。
说明:点、线、面、体之间有如图所示的联系:
例1 :圆锥可以看作是由一个_______旋转得到的( )
A.矩形(长方形) B.等腰梯形
C.半圆 D.直角三角形
思路导引 利用一个三角板绕其直角边旋转即可得到答案。
解:选D
课内达标
1、面和面相交成( )
A、点 B、线 C、面 D、体
2、点动成______;线动成______;面动成_______。
3、飞机飞行表演时在空中留下漂亮的“彩带”。用数学知识解释为___________。
4. 如图,第一行的图形绕虚线旋转一周,便能形成第二行的某个几何体,用线连一连.
课外巩固
1.将下面的直角梯形绕直线l旋转一周,可以得到如下图所示的立体图形的是( ).
2.下列图形中绕直线l旋转一周,能得到右边立体图形的是( )
3.圆锥的侧面和底面相交成______条线,这条线是______的(填“直”或“曲”)
4.长方形纸片绕它的一边旋转形成了一个圆柱体,这说明了 .
5.边长为2厘米和4厘米的长方形绕其一边旋转得到的几何体的表面积为
6. 将下列图形按要求分类:
(1)若按柱、锥、球划分;(2)若按组成面的曲或平划分.
7. 第二行的图绕直线旋转一周,便能形成第一行的某个几何体,用线连一连,并指出这些几何体的名称.
8.将一个长方形绕它的一边所在的直线旋转一周,得到的几何体是圆柱,现在有一个长为4厘米,宽为3厘米的长方形,分别绕它的长、宽所在的直线旋转一周,得到不同的圆柱体,它们的体积分别是多大?
4.2.1直线、线段、射线
第一课时
名师归纳与点拨
知识点1直线、线段、射线的概念及表示
1.直线是向两个方向无限延伸着的;直线上两个点和它们之间的部分叫做线段;直线上的一点和它一旁的部分叫做射线。
2.表示方法:①直线的表示有两种:一个小写字母或两个大写字母.但前面必须加“直线”两字,如:直线l;直线m,直线AB;直线CD. ②线段的表示也有两种:一个小写字母或用端点的两个大写字母.但前面必须加“线段”两字.如:线段a;线段AB.③射线的表示同样有两种:一个小写字母或端点的大写字母和射线上的一个大写字母,前面必须加“射线”两字.如:射线a;射线OA.
说明:直线和射线都不可度量,而线段可度量。用两个大写字母表示射线时注意端点字母要写在前。
知识点2:直线的基本性质:经过两点有一条并且只有一条直线
说明: 这条性质也被称为“直线公理”。“有”表示“存在性”,“只有”表示“唯一性”。
例1 判断下列说法是否正确
1.射线EO和射线OE是同一条射线( )
2.直线比射线长 ( )
3.延长射线OA到B ( )
4.线段AB与线段BA是同一条线段 ( )
思路导引 1.两个大写字母表示射线时,端点字母要在前;2.直线和射线都不可度量;3.射线不可度量;4.线段有两个端点,用两个大写字母表示时与端点字母顺序无关。
解:1.错 2.错 3.错 4.正确
例2.下面图形有几条线段?
思路导引:方法一:以线段的端点为顺序,从左向右观察以A为左端点的线段有几条?AB、AC、AD一共有三条。以B为左端点的线段有几条?BC、BD一共有两条。以C为左端点的线段有几条?一条。
解:3+ 2+ 1=6(条)
课内达标
1. 下面几种表示直线的写法中,错误的是( ).
A.直线a B.直线Ma C.直线MN D.直线MO
2. 在墙上钉一根木条需_______个钉子,其根据是________ .
3. 如图所示,直线_______和直线______相交于点P;直线AB和直线EF相交于点______;点R是直线________和直线________的交点.
4. 探索规律:
(1)若直线L上有2个点,则射线有_____条,线段有______条; ( http: / / www. / / )
(2)若直线L上有3个点,则射线有_____条,线段有______条;
(3)若直线L上有4个点,则射线有_____条,线段有______条;
(4)若直线L上有n个点,则射线有_____条,线段有______条.
课外巩固
1. 下列说法中,正确的是( )
A.射线OA和射线AO表示同一条射线.
B.延长直线AB.
C.经过两点有一条直线,并且只有一条直线.
D.延长射线AB
2.下列四个图中的线段(或直线、射线)能相交的是( )
`
A.(1) B.(2) C.(3) D.(4)
3. 如下图所示,点A在直线L______,点B在直线L________.
4. 如图2,图中共有_______条射线,指出其中的两条_____ __.
5. 如图,OA反向延长得射线 ______
6.看图写话:
(1) (2)
7.如图,要在一个长方体的木块上打四个小孔,这四个小孔要在一条直线上,且每两个相邻孔之间的距离相等,画出图形,并说明其中道理.
8.解答下列问题:
(1) 画图表示,两条直线可以把一个平面分成几个部分 三条直线呢
(2)平面上4条直线最多可以把平面分成多少个部分
4.2.2直线、线段、射线
第二课时
名师归纳与点拨
知识点1线段大小比较的两种比较方法:
重叠比较法 将两条线段的各一个端点对齐,看另一个端点的位置.
数量比较法 用刻度尺分别量出线段AB和线段CD的长度,将长度进行比较.
说明:常用的是数量比较法。
知识点2 线段的性质公理
“两点之间的所有连线中,线段最短”
说明:要强调两点之间的线段的长度叫两点间的距离,而不是两点间的线段;
线段是图形,线段的长度是数值。
例1.点P是线段AB的中点,点C、D把线段AB三等分。已知线段CP的长为1.5cm,求线段AB的长。
思路导引 先得到线段CP与线段AB之间的长度比,就能求出线段AB的长。
解:∵ 点P把线段二等分,
∴ AP=PB=1/2AB
∵ 点C、D把线段AB三等分,
∴ AC=CD=DB=1/3AB
∴ AP-AC=1/2AB-1/3AB=1/6AB, 即 CP=1/6AB
∴ AB=6CP=6×1.5=9cm
即AB的长为9cm
课内达标
1. 在直线上顺次取A、B、C三点,使得AB=5㎝,BC=3㎝,如果O是线段AC的中点,那么线段OB的长度是( )
A.2㎝ B.0.5㎝ C.1.5㎝ D. 1㎝
2. 如图,学生要去博物馆参观,从学校A处到博物馆B处的路径共有⑴、⑵、⑶三条,为了节约时间,尽快从A处赶到B处,假设行走的速度不变,你认为应该走第________条线路(只填番号)最快,理由是___________________。
3.若AB=BC=CD那么AD= AB AC= AD
4. 线段AD=6cm,线段AC=BD=4cm ,E、F分别是线段AB、CD中点,求EF。
课外巩固
1. .如果点C在AB上,下列表达式①AC=AB;②AB=2BC;③AC=BC;④AC+BC=AB中, 能表示C是AB中点的有( )
A.1个 B.2个 C.3个 D.4个
2.如图,从A到B有3条路径,最短的路径是③,理由是( )
A.因为③是直的 B.两点确定一条直线
C.两点间距离的定义 D.两点之间,线段最短
3. 如图,点B、C在线段AD上,则
AC =_______+______ = ______—______,
BC =______—______ = ______—______。
4..已知A,B,C为直线l上的三点,线段AB=9cm,BC=1cm,那A,C两点间的距离是
5. 长为12cm的线段AB上有一点P,M,N分别为PA,PB的中点,则线段MN= ______
6. 量出线段的长度,并比较:
(1)AB=_________cm;AC=_________cm;
AD=_________cm;AE=_________cm。
(2)比较线段的长度。
7. 试用叠合法比较线段:
8. 右图中,线段AB长为24cm,若AD长是CD长的一半少6cm,BC是CD的长的一半多1cm,求线段CD的长度。
4.3.1角
第一课时
名师归纳与点拨
知识点1 角的定义:
静态定义:有公共端点的两条射线组成的图形叫做角,这个公共端点是角的顶点,这两条射线是角的两条边.
说明:公共端点A叫做该角的顶点, 射线AB、AC叫做该角的两条边,
角的符号:∠
动态定义:角也可以看作是一条射线绕着它的端点旋转而形成的图形。
知识点2 角的表示方法:
①用三个字母∠AOB或∠BOA 或用角的顶点∠O②用希腊字母记作∠α③用小写的数字记作∠1
说明:用单个大写字母表示,顶点处只能有一个角
例1.判断下列哪些图形是角
① ② ③ ④
思路导引 根据角的静态定义:“有公共端点的两条射线组成的图形叫做角,这个公共端点是角的顶点,这两条射线是角的两条边”.
解:①③④
例2.如图,(1)图中共有几个角?请把它们表示出来.
(2)能把∠AOB记作∠O吗 为什么 ∠AOB还可以怎样表示呢?
思路导引 一个顶点处不止一个角时,就不能用一个大写字母表示角。
解:(1)图中共有三个角,分别是:∠AOB、∠AOC、∠BOC
(2)不能,因为“一个顶点处不止一个角时,就不能用一个
大写字母表示角”,∠AOB还可以表示为∠BOA.
课内达标
1. 下列语句正确的是( )
A.两条直线相交,组成的图形叫做角
B.两条有公共端点的线段组成的图形叫角
C.两条有公共点的射线组成的图形叫角
D.从同一点引出的两条射线组成的图形叫角
2.用三个大写字母表示角:
∠1为 ;∠ 2为 ;
∠3为 .; 可以用一个大写字母表示的角是______
3. 图中以OC为边的角有______个,它们分别是______
4.以O为顶点的角有几个,请分别把他们写出来。
课外巩固
1. 下列四个图形中,能用∠1,∠AOB,∠O三种方法表示同一个角的是 ( )
2.如图,图中共有( )个角.
(A) 6 (B)7 (C)8 (D)9
3.如下左图所示,把图中用数字表示的角,改用大写字母表示分别是________.
4.将上右图中的角用不同的方法表示出来,填入下表:
∠1 ∠3 ∠4
∠BCA ∠ABC
5.用三个字母表示图中所注的∠1、∠2、∠3:
(1) (2) (3)
∠1是______; ∠1是______; ∠1是______;
∠2是______; ∠2是______; ∠2是______;
∠3是______; ∠3是______; ∠3是______;
∠4是______.。
6如图,图中能用一个大写字母表示的角有几个 分别把它们表示出来.
7.如图,(1)中有几个角?(2)中有几个角;(3)中有几个角.以此类推,若从一点o引n条射线,则以点0为顶点的角【最大的角都小于平角】有几个?
8.想一想,做一做.
(1)用字母表示图中的每个城市.
(2)请用字母在下图分别表示以北京为中心的每两个城市之间的夹角.
( http: / / www. / )
4.3.1角
第二课时
名师归纳与点拨
知识点1 角的度量方法:
计量角的大小常用的单位是“度”,用符号“°”表示。把半圆平均分成180份,每一份所对的角叫做1度的角,记作1°。使用量角器的方法:把量角器放在角的上面,使量角器的中心和角的顶点重合,零度刻度线和角的一条边重合,角的另一条边所对的量角器上的刻度,就是这个角的度数
说明:度量角的工具:一般用量角器
知识点2 以度、分、秒为单位的角度制规定,
把一个周角_等分为360份_____,每一份叫做1度,记作___1°___;把1度的角__等分为60份____,每一份叫做1分,记作___1′___;把1分的角__等分为60份____,每一份叫做1秒,记作___1″___.这样,1周角是_360____°,1平角是__180____°,1°=__60____',1′=___60___″.
例1:时钟在5点15分时,时钟的时针与分针所成的角是多少度?
思路导引 根据钟面上时针走一圈(360°)需要12小时=12*60=720分钟,即时针的速度是360/720=0.5°/分钟;分针走一圈(360°)需要1小时=60分钟,即时针的速度是360/60=6°/分钟.即时针走过一小时在钟面上扫过30°,分针在钟面上走过一分钟扫过6°。
解:所以时针离开12点的角度为5*30°+15*0.5°=157.5°,
分针离开数字12的角度为15*6°=90°,
157.5°-90°=67.5°。
所以5点15分时,时钟的时针和分针所成的锐角是67.5°。
课内达标
1. 在钟表上,1点30分时,时针与分针所成的角是( ).
A.150° B.165° C.135° D.120°
2.如图,量出图中三个角的度数分别是__________,这三个角的和是_____.
3.如图所示,点O在直线AB上,图中小于180°的角共有 个
4.如下图,分别确定四个城市相应钟表上时针与分针所成角的度数.
课外巩固
1. 下列各角中,不可能是钝角的角是( ).
A.周角 B.平角 C.钝角 D.直角.
2. 下列说法正确的是( )
(A)一个周角就是一条射线 (B)平角是一条直线
(C)角的两边越长,角就越大 (D)∠AOB也可以表示为∠BOA
3.用一副三角板可以拼出________的角.
4. 30.6°=_____°_____′=_______′
5. 时钟从3点15分走到3点35分,它的分针转过________度.
6.计算:
(1)53°28′+47°32′; (2)17°50′-3°27′;
7.已知:如图,AOB是直线,∠1∶∠2∶∠3=1∶3∶2,求∠DOB的度数.
8. 小明先在笔直的路AB上行走,走道B点后拐了个弯,然后在笔直的路BC上行走,走到C点后, 又拐了个与刚才相同角度的弯.请画出拐弯后的行走路线
4.3.2角的比较与运算
名师归纳与点拨
知识点1 角的大小比较的两种方法:
一种方法为度量法:可以用量角器量出角的度数,然后比较它们的大小,另一种方法为叠合法:即把他们叠合在一起比较大小。
说明:1.在用叠合法比较两角大小时,顶点必须重合,一边必须重合,另一边落在其余一边的圆旁。2.角的大小只与角两边的张大张小有关,而与角的边画出部分长短无关。3.角的和、差、倍、分的度数,等于它们度数的和、差、倍、分。
知识点2 把一个角分成相等的两个角的射线叫做这个角的平分线,类似的还有角的三等分线等。
说明:角平分线的画法一般有两种
(1)借助量角器画图:以已知角顶点为顶点,已知角的一边为边,在已知线的内部画一个度数等于已知角度数一半的角,则这个角的另一边就是已知角的平分线.
(2)用折叠方法:把角沿顶点对折,使角的两边重合,沿折痕在角的内部画一条射线即为已知角的平分线.
说明:角平分线也是一条射线,角平分线在角的内部,角平分线分成的两个角度数相等。
例1.已知O为直线AB上一点,∠AOC的平分线OM,∠BOC的平分线为ON,求∠MON的度数?
思路导引 根据平角的定义可知∠AOB=180°,再根据OM平分∠AOC,则2∠MOC=∠AOC,同理可得2∠NOC=∠BOC,而
∠AOC+∠BOC=180°,所以2∠MOC+2∠NOC=180°,
∠MOC+∠NOC=90°
解: ∠MON的度数为90°.
课内达标
如图,射线OD是平角∠AOB的平分线,∠COE=90°,那么下列式子中错误的是( ).
(A)∠AOC=∠DOE (B)∠COD=∠BOE
(C)∠AOD=∠BOD (D)∠BOE=∠AOC
2.如图,∠AOB∠COD,则∠1 ∠2(填“<,>, =”)
3.如图,用“=”或“>”或“<”填空:
(1)∠AOC_______∠AOB+∠BOC; (2)∠AOC_______∠AOB;
(3)∠BOD-∠BOC______∠DOC;
4. 如图,已知:∠BOC=2∠AOB,OD平分∠AOC,∠BOD=140求:∠AOB的度数。
课外巩固
1. 射线OC在∠AOB的内部,下列四个式子中不能判定OC是∠AOB的平分线的是( ).
(A)∠AOB=2∠AOC (B)∠BOC=∠AOC
(C)∠AOC∠AOB (D)∠AOC+∠BOC=∠AOB
2. .如图,OC是∠AOB的平分线,OD平分∠AOC,且∠COD=25°,则∠AOB=( ).
(A)100° (B)75°
(C)50° (D)20°
3. 如图,OM是∠AOB的平分线且∠AOM=30°,
则∠BOM=______;∠AOB=______.
4.如图,在横线上填上适当的角:
(1)∠AOC=______+______;
(2)∠AOD-∠BOD=______;
(3)∠BOC=______-∠COD;
(4)∠BOC=∠AOC+______-______.
5.按图填空:
(1)∠ABC是∠ABD与∠DBC的______;
(2)∠BDC是∠ADC与∠ADB的_______.
6. 下面是小马虎解的一道题.
题目:在同一平面上,若∠BOA=70°,∠BOC=15°,求∠AOC的度数.
解:根据题意可画出下图.
∵∠AOC=∠BOA-∠BOC
=70°-15°
=55°,
∴∠AOC=55°.
若你是老师,会给小马虎满分吗 若会,说明理由.若不会,请将小马虎的错误指出,并给出你认为正确的解法.
7. 如图,OD、OE分别是∠AOC和∠BOC的平分线,∠AOD=40°,∠BOE=25°,求∠AOB的度数.
解:∵OD平分∠AOC,OE平分∠BOC,
∴∠AOC=2∠AOD,
∠BOC=2∠______.
∵∠AOD=40°,∠BOE=25°,
∴∠BOC=______,
∠AOC=______.
∴∠AOB=____.
8. 如图,∠AOB的平分线为OM,ON为∠MOA内的一条射线,OG为∠AOB外的一条射线,某同学经过认真的分析,得出一个关系式是∠MON=(∠BON-∠AON),你认为这个同学得出的关系式是正确的吗 若正确,请把得出这个结论的过程写出来。
4.3.3 余角与补角
第一课时
名师归纳与点拨
知识点1余角与补角的定义
如果两个角的和等于90°(直角),就说这两个角互为余角,即其中一个角是另一个角的余角;如果两个角的和等于180°(平角),就说这两个角互为补角,即其中一个角是另一个角的补角.
说明:互余互补是两个角之间的关系,且互为余角是两角之和等于90°(直角),互为补角是两角之和等于180°(平角).“互为”一词的意思,于是得到: 互余、互补的角总是成对出现的.
知识点2余角与补角的性质
①等角的余角相等②等角的补角相等
说明:等(或同)角的余(或补)角相等”这一性质在今后的角度转换中经常用到,应引起重视.
例1:如图,直线AB与CD相交于一点,那么∠1=∠2吗?试说明理由.
思路导引:∵直线AB与CD相交于一点O(已知)
∴∠1与∠3互为补角,∠2与∠3互为补角(互为补角的定义)∴∠1=∠2(等角的补角相等)
解:∠1=∠2
例2:如图,∠AOB是直角,∠COD=90°,OB平分∠DOE,则∠3与∠4是什么关系?并说明理由.
思路导引:∵∠AOB是直角,∠COD=90°(已知)
∴∠1+∠2=90°,∠1+∠3=90°(互为余角的定义)
∴∠2=∠3(等角的余角相等)
∵OB平分∠DOE(已知)
∴∠2=∠4(角平分线的定义)
∴∠3=∠4(等量代换)
解:∠3=∠4
课内达标:
1.已知:如图,∠AOB=∠COD=90°,则∠1与∠2的关系是 ).
(A)互余 (B)互补
(C)相等 (D)无法确定
2.若一个角的余角和它的补角互补,那么这个角为______度。
3.一个角的4倍和这个角的余角互补,这个角是______度。
4. 如图,∠AOC=∠BOD=90 ,∠AOD=130 ,求∠BOC的度数。
课外巩固
1. 互为余角的两个角之差为35°,则较大角的补角是( )
A.117.5° B.112.5° C.125° D.127.5°
2、正确的有( )
⑴一个角的补角一定是钝角,⑵互补的两个角不可能相等,(3)∠A的补角与∠A的余角的差一定等于直角(4)两个锐角一定互为余角,(5)直角没有补角,(6)如果∠MON=180 ,那么M、O、N三点在一条直线上。
A、1个;B、2个;C、3个;D、4个
3. 若∠ 与∠ 互补,∠ 与∠ 互余,则∠ 与∠ 的差为____________.
4.如图,已知A,O,E三点在同一条直线上,OB平分∠AOC,OD平分∠COE,则∠BOC与∠COD的关系为____________.
5. 如图,∠ACB=∠CDB=90 ,图中∠ACD的余角有 个。
6.填写下列空白和理由 ,如右图,
∵∠AOB+∠BOC+∠COD+∠DOA=1周角,
∴∠AOB+∠BOC+∠COD+∠DOA=360°.
(理由_____________________.)
∵∠AOB=∠COD=90°,
∴∠AOD+∠BOC=180°.
(理由:__________________)
又∵∠BOC=42°,
∴∠AOD=180°-∠BOC=180°-42°=__________.
7. 如图所示,∠AOC=90°,OB⊥OD,则与∠BOC相等的角有谁?图中共有多少对互为余角请写出来。
8.如图,O是直线AB上的一点,OM是∠AOC的角平分线,ON是∠BOC的角平分线,
(1)图中互余的角有几对?请写出来。
(2)图中互补的角有几对?请写出来。
4.3.3 余角与补角
第二课时
名师归纳与点拨
知识点1用角度表示方向:一般以正北、正南为基准,用向东或向西旋
转的角度表示方向,如图所示,OA方向可表示为北偏西60 。
说明:(1)用量角器画这样的射线OA时要注意:(1)是以正南或者是正北方向
做角的始边,(2)要理解偏东,偏西的意义。
(3)正北,正南,正西,正东,射线OD OC OB OA
西北方向:射线OE;西南方向:射线OF东南方向:射线OG;东北方向:射线OH
直线AB和直线CD互相垂直,所成四个角均为直角
知识点2 如何表示乙地对甲地的方位角
1. 先找出中心点,然后画出方向指标
2. 把中心点和目的地用线连接起來
3.度量向北的射线和视线之间的角度
例1. 如图,A地和B地都是海上观测站,从A地发现它的北偏东50°方向上有一艘船,同时从B地发现这 艘船在它的北偏东30°方向,试在图中确定这艘船的位置。
思路导引:找到A地北偏东50°和B地北偏东30°的射线。两条射线的交点即为这艘轮船的位置。
解:
课内达标
1.轮船航行到C处测得小岛A的方向为北偏西32°,那么从A观测此时的C处的方向为( ).
(A)南偏东32° (B)东偏南32°
(C)南偏东68° (D)东偏南68°
2.若轮船甲自A岛沿北偏东45°的方向行驶30海里到达B岛,轮船乙自A岛沿南偏西
70°的方向行驶50海里到达C岛,则∠BAC=____________.
3. 如图,由A到B的方向是 ____________
4..在图中画出表示下列方向的射线:
(1)南偏西30° (2)南偏东25°
(3)北偏西20° (4)北偏东65°
(5)东北方向 (6)西南方向
课外巩固
1.A看B的方向是北偏东21°,那么B看A的方向( )
A:南偏东69° B:南偏西69° C:南偏东21° D:南偏西21°
2.如图,下列说法中错误的是( )
A: OC的方向是北偏东60°
B: OD的方向是南偏东60°
C: OB的方向是西南方向
D: OA的方向是北偏西22°
3.在点O 北偏西60°的某处有一点A,在点O南偏西20°的某处有一点B,则∠AOB的度数是_____
4.如图,甲从A点出发向北偏东70°方向走50m至点B,
乙从A出发向南偏西15°方向走80m至点C,则∠BAC的度数是_____
5.说出B在A的____,那么A在B的______.
6.如图,分别指出A,B,C,D在O的什么方向
7. 如图所示,A、B两条海上巡逻艇同时发现海面上有一不明物体,A艇发现该不明物体在它的东北方向,B艇发现该不明物体在它的南偏东60°的方向上, 请你试着在图中确定这个不明物体的位置.
8.小明从点A出发向北偏西50°方向走了3米,到达点B,小林从点A出发向南偏西40°方向走了4米,试画图确定出A、B、C三点的位置(用1厘米表示3米),并从图上求出B点到C点的实际距离
章末总结复习
知识体系构建
知识:(一)多姿多彩的图形
立体图形:棱柱、棱锥、圆柱、圆锥、球等。
1、几何图形
平面图形:三角形、四边形、圆等。
主(正)视图---------从正面看
2、几何体的三视图 侧(左、右)视图-----从左(右)边看
俯视图---------------从上面看
3、点、线、面、体
(1)几何图形的组成
点:线和线相交的地方是点,它是几何图形最基本的图形。
线:面和面相交的地方是线,分为直线和曲线。
面:包围着体的是面,分为平面和曲面。
体:几何体也简称体。
(2)点动成线,线动成面,面动成体
(二)直线、射线、线段
1、基本概念
直线 射线 线段
图形
端点个数 无 一个 两个
表示法 直线a直线AB(BA) 射线AB 线段a线段AB(BA)
作法叙述 作直线AB;作直线a 作射线AB 作线段a;作线段AB;连接AB
延长叙述 不能延长 反向延长射线AB 延长线段AB;反向延长线段BA
2、直线的性质
经过两点有一条直线,并且只有一条直线。
简单地:两点确定一条直线。
3、线段的中点(二等分点)、三等分点、四等分点等
定义:把一条线段平均分成两条相等线段的点。
图形:
A M B
符号:若点M是线段AB的中点,则AM=BM=AB,AB=2AM=2BM。
4、线段的性质
两点的所有连线中,线段最短。简单地:两点之间,线段最短。
5、两点的距离
连接两点的线段长度叫做两点的距离。
6、点与直线的位置关系
(1)点在直线上 (2)点在直线外。
(三)角
1、角:由公共端点的两条射线所组成的图形叫做角。
2、角的表示法(四种):
3、角的度量单位及换算
4、角的分类
∠β 锐角 直角 钝角 平角 周角
范围 0<∠β<90° ∠β=90° 90°<∠β<180° ∠β=180° ∠β=360°
5、角的和、差、倍、分及其近似值
6、角的平线线
定义:从一个角的顶点出发,把这个角分成相等的两个角的射线叫做角的平分线。
7、互余、互补
(1)若∠1+∠2=90°,则∠1与∠2互为余角。其中∠1是∠2的余角,∠2是∠1的余角。
(2)若∠1+∠2=180°,则∠1与∠2互为补角。其中∠1是∠2的补角,∠2是∠1的补角。
(3)余(补)角的性质:等角的补(余)角相等。
8、方向角
(1)正方向
(2)北(南)偏东(西)方向
能力:1.能判断简单物体(直棱柱、圆柱、圆锥、球)的三视图。
2.能根据三视图描述基本几何体或实物原型。
3.能根据展开图判断立体模型。
4.能借助量角器能画出给定度数的角。
5.能正确的分辨并表示方位角
方法:1. 用“度量法”和“用尺规作图法”画一条线段等于已知线段,并用“度量法”和“叠合法”比较线段的大小
2. 用“度量法”和“叠合法”比较角的大小
3.借助三角尺能画出15°的倍数的角,在0~180°之间共能画出11个角。
4.用尺规作图法画出一个角与已知角相等
综合题型剖析
已知如图,线段AD=6,线段AC=BD=4,E,F分别是线段AB,CD的中点,求EF。
思维导引 因为AC=BD=4,所以
可得AC+BC+BC+CD=8,又知道AB+BC+CD=6,所以可以求得BC=8-6=2,因此也可推出AB=2,CD=2,又根据E,F分别是AB,CD的中点可知,EB=1,CF=1,因此可求得EF.
解:
点拨:此题关键是由AC+BD=8cm,把线段分解以后气的BC的长。
例2. 若∠AOB=∠COD=∠AOD,已知∠COB=80°,求∠AOB、∠AOD的度数
思路导引 因为已知∠AOB=∠COD=∠AOD,所以可设∠AOB=x°,则可推出∠COD=x°,∠AOD=6 x°,有根据图可以知道∠AOD=∠AOB+∠COB+∠COD,因此可以推出∠COB=4 x°,又告诉了∠COB=80°,所以可求出图中所有角的度数。
解:
点拨: 根据条件推导出∠COB=4 x°=80°是本题的关键所在。
例3.如图所示,学校、工厂、电视塔在平面图上的标点分别是A、B、C,工厂在学校的北偏西30°电视塔在学校的南偏东15°,则平面图上的∠BAC应是多少度?
思路导引 这是关于方位角的问题,现在要求∠BAC的度数,首先应明白∠BAC是由∠BAD和∠CAD组成的,然后根据条件即可解出∠BAC的度数。
解:
点拨: 解此题时一定要搞清方位角的大小。
综合练习巩固
选择题
1.在以下四个图形中,经过折叠能围成一个正方体的是( )
2.如图,能用∠1,∠ACB,∠C三种方法表示同一个角的是 ( )
3. ①平角是一条直线;②射线是直线的一半;③射线AB与射线BA表示同一条射线;④用一个扩大2倍的放大镜去看一个角,这个角会扩大2倍;⑤两点之间,线段最短;⑥120.5°= 120°50 .
以上说法正确的有( )
A .0个 B.1个 C.2个 D.3个
二.填空题
4.已知中,,,的平分线交于点,则的度
数为
5.已知互余两角的差为,则这两个角的度数分别为
6. 如图,AB=16 cm,C是AB上一点,且AC=10 cm,D是AC的中点,E是BC的中点,则线段DE的长度为
三,解答题
7. 如图所示,∠AOC=90°,OB⊥OD,则与∠BOC相等的角有谁?图中共有多少对互为余角请写出来。
8. 如图,OA的方向是北偏东15°,OB的方向是西偏北50°。
(1)若∠AOC=∠AOB,则OC的方向(方位角)是____
(2)OD是OB的反向延长线,OD的方向是(方位角)是_________;
(3)∠BOD可看作是OB绕点O逆时针方向至OD,
作∠BOD的平分线OE,并用方位角表示OE的方向。
(4)在(1)、(2)、(3)的条件下,求∠COE。
学业水平测试
1. .(2010·滨州中考)
2. (2008·十堰中考)如图,C、D是线段AB上两点,若CB=4cm,DB=7cm,且D是AC的中点,则AC的长等于( )
A.3cm B.6cm C.11cm D.14cm
3.(2010·凉山中考)将一副三角板按图中的方式叠放,则角等于( )
A. B. C. D.
4. .(2009·长沙中考)如图,于点是的平分线,则的度数为 .
5.(2009·云南中考)如图,点C是线段AB上的点,点D是线段BC的中点,若AB=10,AC=6 ,则CD=_______________.
( http: / / )
6.(2009·枣庄中考)如图,将一副三角板叠放在一起,使直角顶点重合于O点,则 .
7. (2010湖南娄底)如图6,直线AB、CD相交于点O,OE平分∠AOD,若∠BOD=100°,求∠AOE的度数。
8. (2009山东枣庄)如图,将一副三角板叠放在一起,使直角顶点
重合于O点,求的度数。
9.(2010 嵊州市)如图,平面内有公共端点的六条射线OA,OB,OC,OD,OE,OF,从射线OA开始按逆时针方向依次在射线上写出数字1,2,3,4,5,6,7,….
(1)“17”在射线 上.)
(2)请任意写出三条射线上数字的排列规律.
(3)“2007”在哪条射线上?
10.(2010年杭州市)已知直四棱柱的底面是边长为a的正方形, 高为, 体积为V, 表面积等于S.
(1) 当a = 2, h = 3时,分别求V和S;
(2) 当V = 12,S = 32时,求 ( http: / / www. / )的值.
学业水平考试卷
(时间60分钟,满分100分)
班级 姓名 得分
一.选择题(每小题3分,共24分)
下图所示几何体的俯视图是( )
A B C D
2、下列图形中为正方体的平面展开图的是 ( )
A B C D
3.如图7,∠AOE=∠BOC,OD平分∠COE,
那么图中,相等的角共有( )
A.1对 B.2对
C.3对 D.4对 <图7>
4. 如图,能用∠1,∠ACB,∠C三种方法表示同一个角的是 ( )
5. ①平角是一条直线;②射线是直线的一半;③射线AB与射线BA表示同一条射线;④用一个扩大2倍的放大镜去看一个角,这个角会扩大2倍;⑤两点之间,线段最短;⑥120.5°= 120°50 .
以上说法正确的有( )
A .0个 B.1个 C.2个 D.3个
6.如图,AB=16 cm,C是AB上一点,且AC=10 cm,D是AC的中点,E是BC的中点,则线段DE的长度为 ( )
A.6 cm B.8 cm C.10 cm D.12cm
7.如图10,由A到B的方向是( )
A.南偏东30° B.南偏东60°
C.北偏西30° D.北偏西60°
8.如图所示,从O点出发的五条射线,可以组成角的个数是( ).
A.10个 B.9个 C.8个 D.4个
二.填空(每小题3分,共24分)
9.圆柱的侧面展开图是一个 ,圆锥的侧面展开图是一个 ,棱柱的侧面展开图是一个 。
10.北京时间2点30分,钟面上的时针和分针的夹角为 度。
11.如图1,已知CB=5,DB=7.5,D是AC的中点,
则AC=_________ . <图1>
12.126.31°=____°____′___″
13.如图2,CB⊥AB,∠CBA与∠CBD的度数比是4:1,则∠DBA=________度,
∠CBD的补角是_________度.
<图2> <图3>
14.如图3,AC⊥BC,CD⊥AB,点A到BC边的距离是线段_____的长,点B到CD边的距离是线段_____的长,图中的直角有_____________,∠A的余角有_______________,和∠A相等的角有__________.
15. 如图,折叠围成一个正方体时,数字 会在与数字2所在的平面相对的平面上。
16. 如图是由一些相同的小正方体构成的几何体的三视图,这些相同的小正方体的个数是
。
三.解答题
17.作图:(1)(5分)如图,有一个几何体,请画出看它的三视图
18.(5分)已知线段a、b(如图),画出线段AB,设AB=3a-b,并写出画法.
19.计算(每小题2分,共8分)
①.37°28′+44°49′; ②.108°18′-52°30″;
③.25°36′×4; ④ .40°40′÷3.
20.(7分)一个角的余角的两倍比它的补角的 少40°,求这个角的度数.
21. (7分)如图,已知直线和相交于点,是直角,平分,,求的度数.
22.(10分)如图,M是线段AB的中点,点C在线段AB上,且AC=4 cm,N是AC的中点,
MN=3 cm,求线段CM和AB的长
23.(10分)如图,∠AOB是直角,∠AOC等于46°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数.
附加题
已知∠ 与∠ 互为补角,且∠ 互为补角,且∠ 的比∠ 大15°,求∠ 的余角.
4.1.1 几何图形
课内达标
1.D 2,长方形 3.球,正方体4.立体图形:①④⑤⑥⑦;平面图形:②③
课外巩固
1.C 2.A 3. (1) 正方体 (2)长方体 (3) 三棱柱(4)四棱锥 (5)圆柱 4.7,9
5.正方体,球 6. 分析:主视图有2列,第一列3个小正方形,第2列有1个小正方形;左视图有3列,小正方形数目分别为1,3,2;俯视图有3行,小正方形数目分别为1,2,1.
解: 如图:
7.x=1 8.
4.1.2 几何图形
课内达标
B 2. 点动成_线_____;线动成__面____;面动成___体____ 3.点动成线
4.
课外巩固
1. B 2.D 3.一,曲 4.面动成体 5.
6. 思路解析:分类时一定要注意把握好特征,做到不重不漏,标准统一.
答案:(1)柱体:①,③,④,⑤,⑦;锥体:②;球体:⑥
(2)组成的面有曲面:②,⑥,⑦;组成的面是平面:①,③,④,⑤
7. 思路解析:线段旋转一周形成一个圆,长方形旋转一周形成一个圆柱,半圆旋转一周会形成球 答案:(1)与C;(2)与A;(3)与B连起来.A是圆台;B是球;C是圆柱与圆锥的组合.
8.
4.2.1直线、线段、射线
第一课时
课内达标
1. B 2.2,经过两点有且只有一条直线 3. .AB CD O CD EF 4. (1)4 1 (2)6 3 (3)8 6 (4)2n n(n-1)
课外巩固
1.C 2.A 3.上,外 4.2,射线AB,射线BA 5.OE 6.直线AB与直线CD交于点O,点E在直线l上 7. 道理:经过两点,有且只有一条直线 8. (1)4,7(2)11
4.2.2直线、线段、射线
第二课时
课内达标
1.D 2.(2),两点之间,线段最短 3.3, 4.
课外巩固
1.C 2.D 3.AB+BC=AD-CD;AC-AB=BD-CD 4. 5.6cm
6.略 7.略 8.14.5cm
4.3.1角
第一课时
课内达标
1.D 2. ∠EDB, ∠DBE, ∠ABC: ∠A, ∠C, ∠D 3.3, ∠DOC, ∠COB, ∠COA
4. .以O为顶点的角有几个,请分别把他们写出来。
解:共有10个角,
分别是:
∠AOB,∠AOC,
∠AOD,∠AOE,
∠BOC,∠BOD,
∠BOE,∠COD,
∠COE,∠DOE。
课外巩固
1.B 2.A 3. ∠ADE, ∠DEC
4.
5.(1) ∠AGB, ∠ACE, ∠DEC(2) ∠EGB, ∠EHB, ∠CHG(3) ∠DAC, ∠ACB, ∠BAC, ∠ACD
6.3个,∠A,∠B,∠C 7.3,6,10, 8.略
4.3.1角
第二课时
课内达标
1.C 2,略 ,180° 3.9 4. 30°,0°,120°,90°
课外巩固
1.D 2.D 3.75°、105°、135°、120°、15°、30°、150°、180°
4.30,36,216 5.10 6. (1)101° (2)14°23′ 7.30° 8.略
4.3.2角的比较与运算
课内达标
1.D 2.= 3.=,>,= 4.28°
课外巩固
1.D 2.A 3.30°,60°4.
5.和,差 6.55°或者是85°,分OC在角内部及角外部两种情况讨论
7. 解:∵OD平分∠AOC,OE平分∠BOC,
∴∠AOC=2∠AOD,
∠BOC=2∠_ BOE _____.
∵∠AOD=40°,∠BOE=25°,
∴∠BOC=__50°____,
∠AOC=__80°____.
∴∠AOB=__130°__.
8.∠BON=∠BOM+∠MON=1/2∠AOB+∠MON
∠AON=∠BOM-∠MON=1/2∠AOB-∠MON
∠BON-∠AON=(1/2∠AOB+∠MON)-(1/2∠AOB-∠MON)=2∠MON
∠MON=1/2(∠BON-∠AON)
4.3.3 余角与补角
第一课时
课内达标
1.B 2.45° 3.30° 4.50°
课外巩固
1.A 2.B 3.90° 4.互余 5.2个 6.周角的定义,等式基本性质1,138 °
7.
8.。有四对互余的角∠AOM与∠CON,∠AOM与∠BON,
∠COM与∠CON,∠COM与∠BON,3对互补的角:∠BON与∠NOA,∠BOC与∠AOC, ∠BOM 与∠AOM
4.3.3 余角与补角
第二课时
课内达标
1.A 2.155° 3.北偏西60° 4.略
课外巩固
1.C 2.A 3.110° 4.125° 5.北偏西40度,南偏西40度
6.A在O的北偏东60度,B在O的北偏西30度,C在O 的南偏西75度,D在O的西南方向
7.如图
综合练习巩固
1.B 2.C 3.B 4.120° 5.55°或者是35° 6.8cm 7.略 8.北偏东70°,南偏东40°,南偏西40度,北偏东40°,160°
学业水平测试
1.B 2.B 3.A 4.135° 5.2 6.180° 7.40° 8.180°
9. 【解析】(1)“17”在射线上.
(2)射线上数字的排列规律:
射线上数字的排列规律:
射线上数字的排列规律:
射线上数字的排列规律:
射线上数字的排列规律:
射线上数字的排列规律:
(3)在六条射线上的数字规律中,只有有整数解.解为
“2007”在射线上.
10. 答案:
(1) 当a = 2, h = 3时,
V = a2h= 12 ;
S = 2a2+ 4ah =32 .
(2) ∵a2h= 12, 2a(a + 2h) =32,
∴ , (a + 2h) =,
∴===.
学业水平考试卷
1.C 2.C 3.B 4.C 5.B 6.B 7.B 8.10 9.长方形,扇形,长方形 10.105°
11.5 12. ___126_°_18___′__36_″ 13.72°,162° 14.AC, BD, ∠AOC, ∠COD,
∠ACB, ∠ACD, ∠B, ∠DCB 15.5 16.5 17.略
18. 【答案】
方法一:
①量得a=1.9 cm,b=2.6 cm;
②算AB的长,AB=3×1.9-×2.6=4.4(cm);
③画线段AB=4.4 cm.
则线段AB就是所要画的线段.
方法二:
①画射线AM,并在射线AM上顺次截取AC=CD=DE=a;
②在线段EA上截取EB=b.
则线段AB就是要画的线段.
19. 【提示】
1°=60′,1′=60″,低一级单位满“60”,要向高一级单位进“1”,由高一级单位借“1”要化成“60”加入低一级单位参与运算.
【答案】1.82°17′; 2.56°17′30″; 3.102°24′; 4.13°33′20″.
20.40° 21.24°
22. 【提示】CM=MN-NC,AB=2 AM.
【答案】∵ N是AC中点,AC=4 cm,
∴ NC=AC=×4=2(cm),
∵ MN=3 cm,
∴ CM=MN-NC=3-2=1(cm),
∴ AM=AC+CM=4+1=5(cm),
∵ M是AB的中点,
∴ AB=2 AM=2×5=10(cm).
答:线段CM的长为1 cm,AB的长为10 cm.
23. 【提示】
∠MON=∠CON-∠COM.
【答案】
∵ ∠AOB是直角.
∴ ∠AOB=90°(直角的定义),
∵ ∠AOC=46°,
∴ ∠BOC=∠AOB+∠AOC=90°+46°=136°,
∵ ON平分∠BOC,
∴ ∠CON=∠BOC=×136°=68°(角平分线定义),
∵ OM平分∠AOC,
∴ ∠COM=∠AOC=×46°=23°(角平分线定义),
∴ ∠MON=∠CON-∠COM=68°-23°=45°.
答:∠MON=45°.
【点评】
和线段计算一样,在进行有关角度计算时,也要根据已知,仔细看图,找出已知角与所求角的关系,此题中的∠MON还可看成是∠BOM与∠BON的差,∠MON也可看成是∠AOM与∠AON之和,请试一试怎么算,比一比哪种方法较简便.关于角平分线的三种表达式,也应结合图形灵活运用.
附加题:【提示】
互补两角和为180°,根据题意可知列出关于∠ 、∠ 的方程组,求出∠ ,再根据“互余两角和为90°”,求出∠ 的余角.
【答案】
由题意可得:
解之得:
∴ ∠ 的余角=90°-∠ =90°-63°=27°.
答:∠ 的余角是27°.
图4-1-1
A.
B.
C.
D.
建
设
和
谐
昆明
明
图4-1-2
正面
左面
上面
-2
A
x
3
1
3x-2
点
线
面点
体点
动
交
交
交
动
动
③
①
②
C
A
B
O
O
A
C
D
E
A
B
C
O
A
B
D
C
3
1
2
4
A
C
D
B
C
A
D
B
E
3
1
2
4
60
B
C
D
A
A
E
B
C
F
D
O
D
C
B
A
东
D
B
C
A
北
西
南
A.
B.
C.
D.
( )
A
C
B
D
E
O
图6
A
B
C
D
O
1
(第3题图)
A
B
C
D
E
O
