沪教版(五四学制)九年级数学上册24.3三角形一边的平行线课件(共50张PPT)
文档属性
| 名称 | 沪教版(五四学制)九年级数学上册24.3三角形一边的平行线课件(共50张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-28 00:00:00 | ||
图片预览




文档简介
(共50张PPT)
沪教版九年级第一学期
24.3三角形一边的平行线
a:b=c:d
ad=bc
。
a:b=b:c
b?=ac
。
比例的基本性质
合比性质
如果
,那么
。
如果
(
),
等比性质
那么
相似形:对应角相等;对应边成比例
合比性质
如果
,那么
。
如果
,那么
。
如果
,那么
。
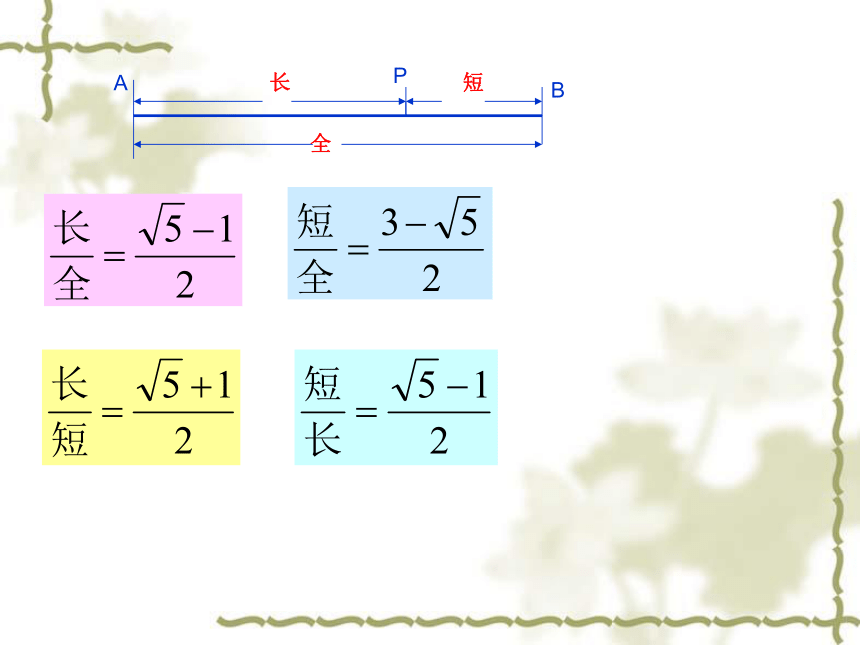
拓展:
A
B
P
全
长
短
A
B
C
A
B
C
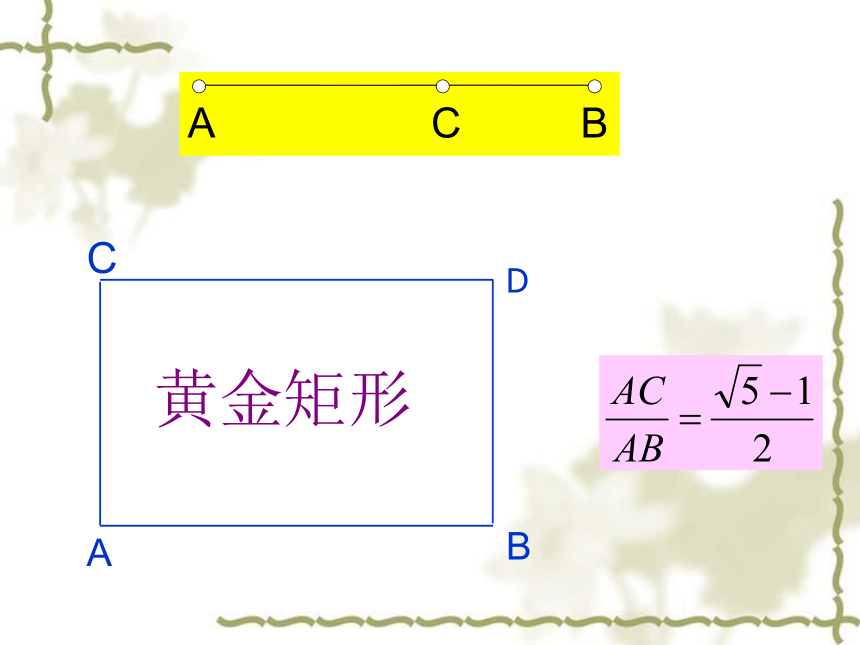
黄金矩形
D
A
B
C
D
E
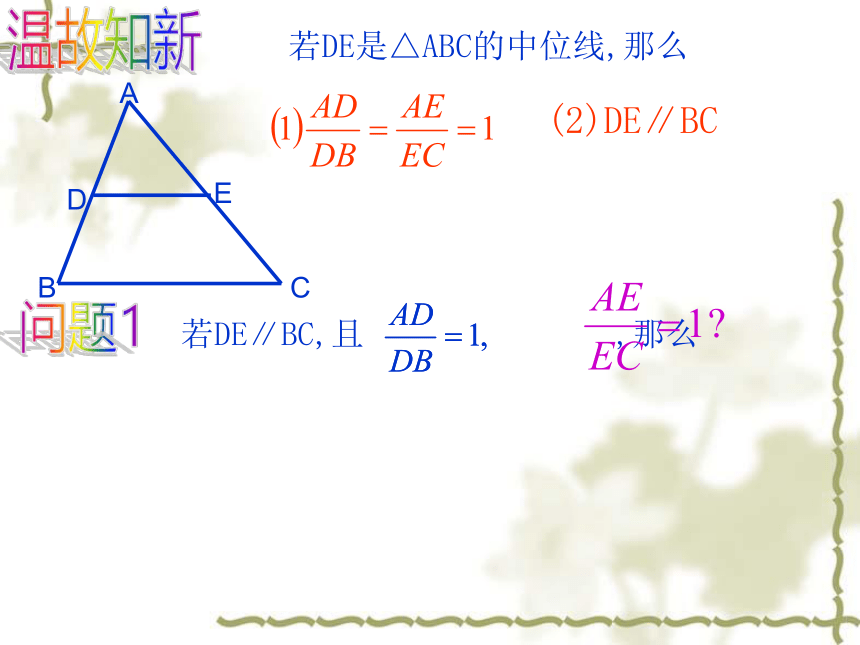
若DE是△ABC的中位线,那么
(2)DE∥BC
若DE∥BC,且
,那么
A
B
C
D
E
A
B
C
D
E
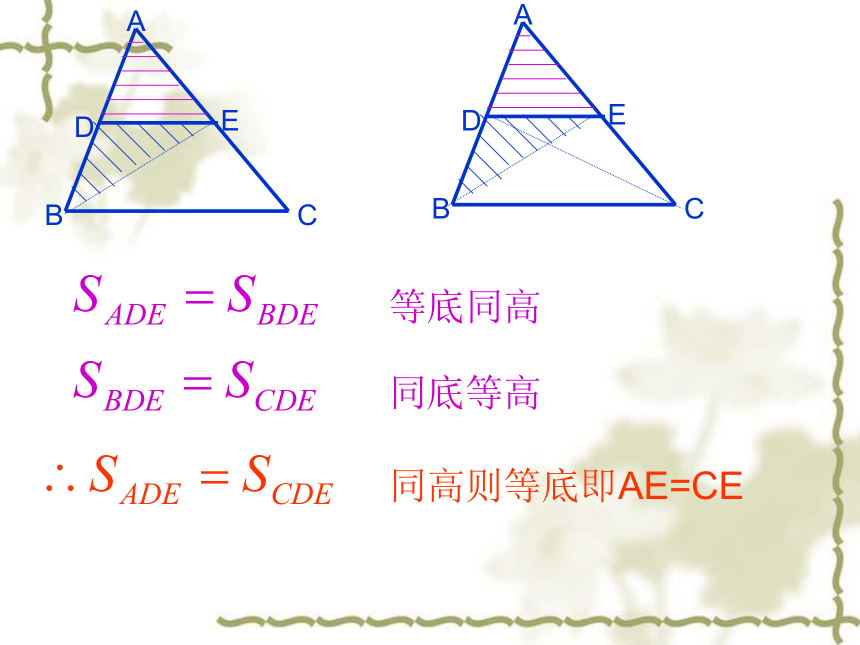
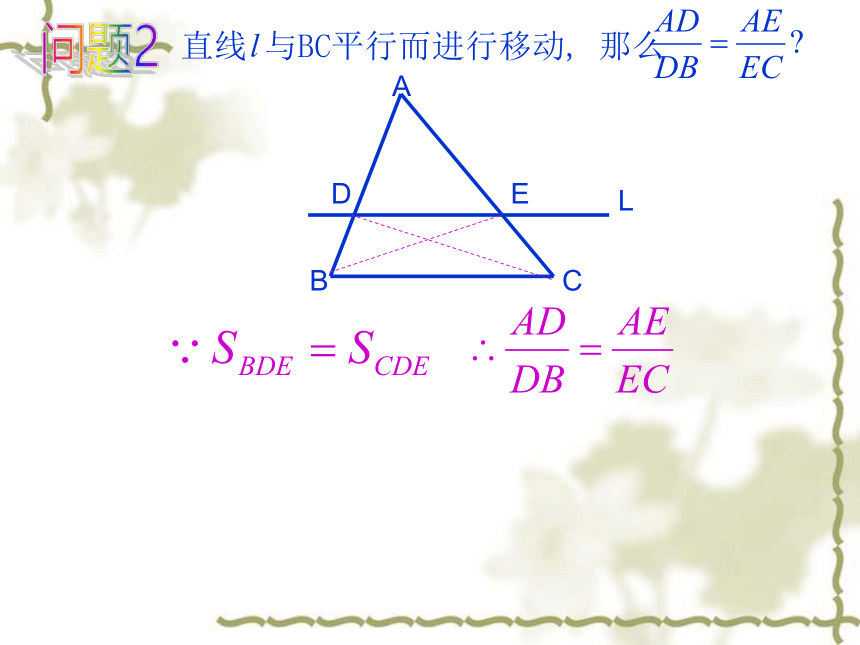
等底同高
同底等高
同高则等底即AE=CE
A
B
C
D
E
L
直线
与BC平行而进行移动,
那么
A
B
C
D
E
L
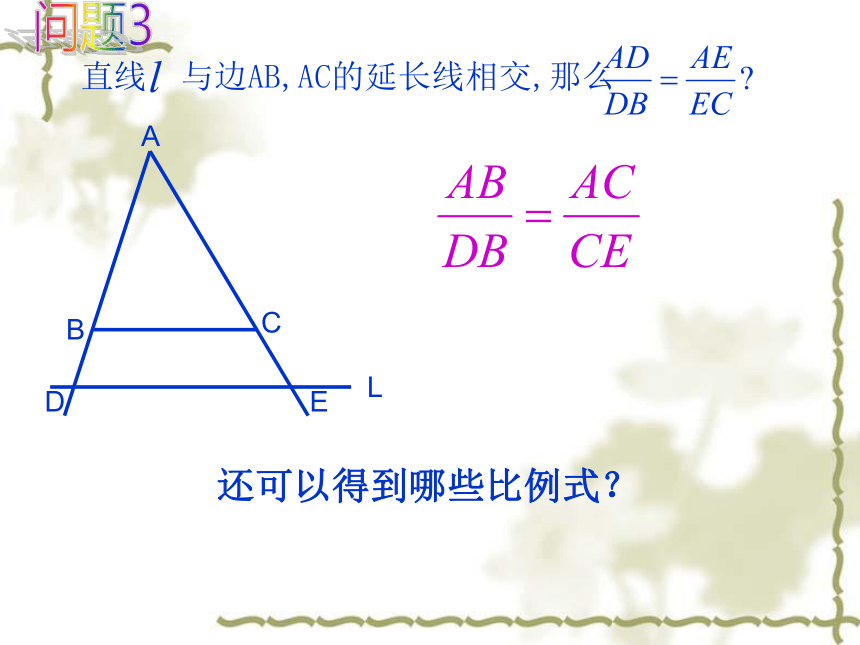
直线
与边AB,AC的延长线相交,那么
还可以得到哪些比例式?
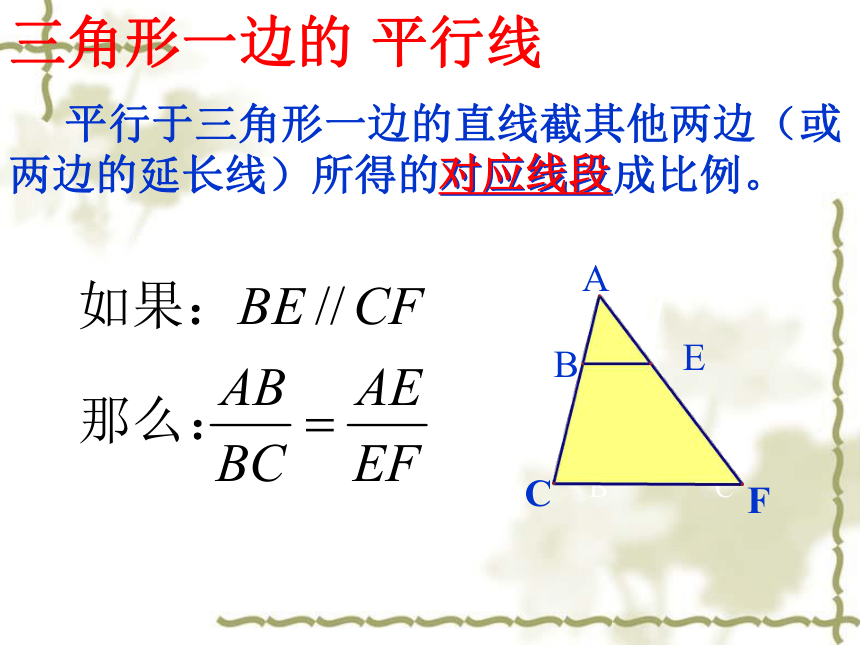
平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例。
三角形一边的
平行线
A
E
D
C
B
E
A
D
C
B
对应线段
A
B
C
E
F
A
E
D
C
B
E
A
D
C
B
A
B
C
E
F
D
平行于三角形一边的直线截其他两边所在的直线,截得的三角形的三边与原三角形的三边对应成比例。
三角形一边的
平行线性质的推论:
A
B
C
D
E
L
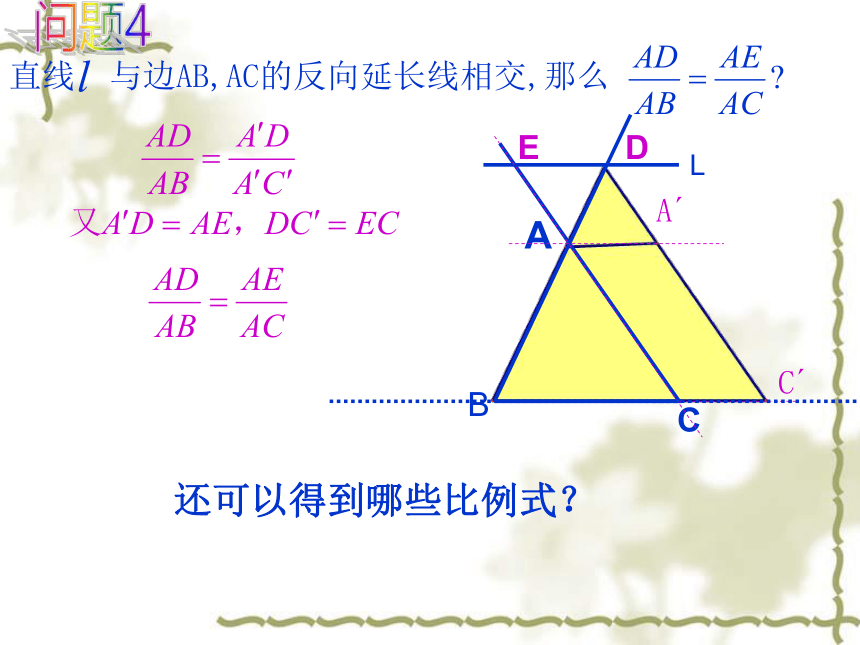
直线
与边AB,AC的反向延长线相交,那么
C?
A?
还可以得到哪些比例式?
A
B
C
l1
l2
l3
D
E
F
当
,AB
BC时
l1∥l2∥l3
A
B
C
l1
l2
l3
D
E
F
平行线分线段成比例定理:
当
AB
BC时
l1∥l2∥l3,
三条平行线截两条直线,所得的对应线段成比例.
A
B
C
D
E
A
D
E
B
C
A
B
C
E
D
平截“A”型
平截“X”型
如果一组平行线在一条直线上截得的线段相等,
那么在其它直线上截得的线段也相等.
例如:
当
l1∥l2∥
l3
,
AB=BC
时,
A
B
C
l1
l2
l3
D
E
F
则有
DE=EF.
例题:
∥
∥
,AB=3,AC=8,DF=10.求DE,EF的长.
A
B
C
D
E
F
略
BE,CF是△ABC的中线,交于点G,
求证:
A
B
C
F
E
G
三角形的三条中线交于一点,这点叫做三角形的重心
三角形的重心到一个顶点的距离,等于它到这个顶点对边中点的距离的两倍.
A
B
C
F
E
G
请说出各个结论……
练习:DE∥BC,
2BC=3ED,AC=8,AE=?
A
B
C
E
D
课堂练习p13---24.3(1)
p15---24.3(2)
A
B
C
D
E
A
D
E
B
C
A
B
C
E
D
平截“A”型
平截“X”型
如果一条直线平行三角形的一边,那么截其它两边所在的直线所得的对应线段成比例。
如果一条直线平行三角形的一边,那么截得的三角形的三边与原三角形的三边对应线段成比例。
A
B
C
l1
l2
l3
D
E
F
当
AB
BC时
l1∥l2∥l3,
三条平行线截两条直线,所得的对应线段成比例.
三角形的三条中线交于一点,这点叫做三角形的重心
三角形的重心到一个顶点的距离,等于它到这个顶点对边中点的距离的两倍.
A
B
C
F
E
G
A
B
C
D
E
若
,那么DE∥BC?
∴等高,推出□,∴DE∥BC
三角形一边的平行线判断定理
如果一条直线截三角形的两边所得的对应线段成比例,那么这条直线平行于三角形的第三边.
A
B
C
D
E
推出DE∥BC
三角形一边的平行线判断定理推论
如果一条直线截三角形的两边的延长线(在第三边的同侧)所得的对应线段成比例,那么这条直线平行于三角形的第三边.
三角形一边的平行线判断定理推论
如果一条直线截三角形的两边的延长线(在第三边的同侧)所得的对应线段成比例,那么这条直线平行于三角形的第三边.
A
B
C
D
E
E?
这里DE=DE?
∴DE∥BC?
A
C
B
E
D
F
例题:
DE∥BC,
求证:EF∥DC
例题6
已知线段a,b,c.求作线段x,使a∶b=c∶x
a
b
c
a
b
c
x
O
M
N
作法略
练习:P18—24.3(3)
P20—24.3(4)
A
B
C
l1
l2
l3
D
E
F
当
AB
BC时
l1∥l2∥l3,
三条平行线截两条直线,所得的对应线段成比例.
A
B
C
D
E
A
D
E
B
C
A
B
C
E
D
平截“A”型
平截“X”型
如果一条直线截三角形的两边所在的直线所得的对应线段成比例,那么这条直线平行于三角形的第三边.
A
B
C
D
E
推出DE∥BC
A
B
C
E
D
注意:只是侧面之比
例题:
如图,D是△ABC的BC边上的点,
BD:DC=2:1,
求:BE:EF的值.
D
A
B
C
E中
F
E是AD的中点,
连结BE并延长交AC于F,
D
A
B
C
E
F
n
2k
k
解法1:
过点D作CA的平行线交BF于点P,
P
?y
y
n
y
求:BE:EF的值.
D
A
B
C
E
F
n
解法1:
过点D作CA的平行线交BF于点P,
P
n
2k
k
y
y
4y
?y
∴BE:EF=5:1.
则
∴PE=EF
BP=2PF=4EF,
所以BE=5EF
D
A
B
C
E
F
n
n
2k
解法2:
过点D作BF的平行线交AC于点Q,
y
k
Q
?y
2y
D
A
B
C
E
F
n
n
解法2:
过点D作BF的平行线交AC于点Q,
Q
2k
k
?y
2y
5y
y
∴BE:EF=5:1.
∴
D
A
B
C
E
F
2k
解法3:
过点E作BC的平行线交AC于点S,
S
n
n
k
?k
D
A
B
C
E
F
解法3:
过点E作BC的平行线交AC于点S,
S
n
n
?y
5y
y
2k
k
D
A
B
C
E
F
n
n
2k
解法4:
过点E作AC的平行线交BC于点T,
T
?k
?k
D
A
B
C
E
F
n
n
2k
解法4:
过点E作AC的平行线交BC于点T,
T
y
?y
5y
∵BD=2DC,
∴
∴BE:EF=5:1.
练习:
如图,D是△ABC的BC边上的点,
BD:DC=2:1,
求AF:CF的值.
D
A
B
C
E
F
E是AD的中点,
连结BE并延长交AC于F,
D
A
B
C
E
F
解法1:
过点D作CA的平行线交BF于点P,
P
n
n
2x
2x
2k
k
3x
AF:CF=2:3.
D
A
B
C
E
F
解法2:
过点D作BF的平行线交AC于点Q,
Q
n
n
2x
2x
2k
k
x
AF:CF=2:3.
D
A
B
C
E
F
解法3:
过点E作BC的平行线交AC于点S,
S
n
n
h
2h
4h
y
5y
4y
AF:CF=2:3.
D
A
B
C
E
F
解法4:
过点E作AC的平行线交BC于点T,
T
n
n
h
h
4h
5y
6y
4y
AF:CF=2:3.
拓展与提高
一直线截△ABC三边AB,AC,BC或其延长线于D,E,F,求证;
C
B
A
D
E
F
提示过A作BC的平行线交FD的延长线于G
A
B
C
D
F
E
G
H
P
拓展与提高
如图,大正方形的边长为2,小正方形的边长为1,那么CP∶PF=?
2∶3
沪教版九年级第一学期
24.3三角形一边的平行线
a:b=c:d
ad=bc
。
a:b=b:c
b?=ac
。
比例的基本性质
合比性质
如果
,那么
。
如果
(
),
等比性质
那么
相似形:对应角相等;对应边成比例
合比性质
如果
,那么
。
如果
,那么
。
如果
,那么
。
拓展:
A
B
P
全
长
短
A
B
C
A
B
C
黄金矩形
D
A
B
C
D
E
若DE是△ABC的中位线,那么
(2)DE∥BC
若DE∥BC,且
,那么
A
B
C
D
E
A
B
C
D
E
等底同高
同底等高
同高则等底即AE=CE
A
B
C
D
E
L
直线
与BC平行而进行移动,
那么
A
B
C
D
E
L
直线
与边AB,AC的延长线相交,那么
还可以得到哪些比例式?
平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例。
三角形一边的
平行线
A
E
D
C
B
E
A
D
C
B
对应线段
A
B
C
E
F
A
E
D
C
B
E
A
D
C
B
A
B
C
E
F
D
平行于三角形一边的直线截其他两边所在的直线,截得的三角形的三边与原三角形的三边对应成比例。
三角形一边的
平行线性质的推论:
A
B
C
D
E
L
直线
与边AB,AC的反向延长线相交,那么
C?
A?
还可以得到哪些比例式?
A
B
C
l1
l2
l3
D
E
F
当
,AB
BC时
l1∥l2∥l3
A
B
C
l1
l2
l3
D
E
F
平行线分线段成比例定理:
当
AB
BC时
l1∥l2∥l3,
三条平行线截两条直线,所得的对应线段成比例.
A
B
C
D
E
A
D
E
B
C
A
B
C
E
D
平截“A”型
平截“X”型
如果一组平行线在一条直线上截得的线段相等,
那么在其它直线上截得的线段也相等.
例如:
当
l1∥l2∥
l3
,
AB=BC
时,
A
B
C
l1
l2
l3
D
E
F
则有
DE=EF.
例题:
∥
∥
,AB=3,AC=8,DF=10.求DE,EF的长.
A
B
C
D
E
F
略
BE,CF是△ABC的中线,交于点G,
求证:
A
B
C
F
E
G
三角形的三条中线交于一点,这点叫做三角形的重心
三角形的重心到一个顶点的距离,等于它到这个顶点对边中点的距离的两倍.
A
B
C
F
E
G
请说出各个结论……
练习:DE∥BC,
2BC=3ED,AC=8,AE=?
A
B
C
E
D
课堂练习p13---24.3(1)
p15---24.3(2)
A
B
C
D
E
A
D
E
B
C
A
B
C
E
D
平截“A”型
平截“X”型
如果一条直线平行三角形的一边,那么截其它两边所在的直线所得的对应线段成比例。
如果一条直线平行三角形的一边,那么截得的三角形的三边与原三角形的三边对应线段成比例。
A
B
C
l1
l2
l3
D
E
F
当
AB
BC时
l1∥l2∥l3,
三条平行线截两条直线,所得的对应线段成比例.
三角形的三条中线交于一点,这点叫做三角形的重心
三角形的重心到一个顶点的距离,等于它到这个顶点对边中点的距离的两倍.
A
B
C
F
E
G
A
B
C
D
E
若
,那么DE∥BC?
∴等高,推出□,∴DE∥BC
三角形一边的平行线判断定理
如果一条直线截三角形的两边所得的对应线段成比例,那么这条直线平行于三角形的第三边.
A
B
C
D
E
推出DE∥BC
三角形一边的平行线判断定理推论
如果一条直线截三角形的两边的延长线(在第三边的同侧)所得的对应线段成比例,那么这条直线平行于三角形的第三边.
三角形一边的平行线判断定理推论
如果一条直线截三角形的两边的延长线(在第三边的同侧)所得的对应线段成比例,那么这条直线平行于三角形的第三边.
A
B
C
D
E
E?
这里DE=DE?
∴DE∥BC?
A
C
B
E
D
F
例题:
DE∥BC,
求证:EF∥DC
例题6
已知线段a,b,c.求作线段x,使a∶b=c∶x
a
b
c
a
b
c
x
O
M
N
作法略
练习:P18—24.3(3)
P20—24.3(4)
A
B
C
l1
l2
l3
D
E
F
当
AB
BC时
l1∥l2∥l3,
三条平行线截两条直线,所得的对应线段成比例.
A
B
C
D
E
A
D
E
B
C
A
B
C
E
D
平截“A”型
平截“X”型
如果一条直线截三角形的两边所在的直线所得的对应线段成比例,那么这条直线平行于三角形的第三边.
A
B
C
D
E
推出DE∥BC
A
B
C
E
D
注意:只是侧面之比
例题:
如图,D是△ABC的BC边上的点,
BD:DC=2:1,
求:BE:EF的值.
D
A
B
C
E中
F
E是AD的中点,
连结BE并延长交AC于F,
D
A
B
C
E
F
n
2k
k
解法1:
过点D作CA的平行线交BF于点P,
P
?y
y
n
y
求:BE:EF的值.
D
A
B
C
E
F
n
解法1:
过点D作CA的平行线交BF于点P,
P
n
2k
k
y
y
4y
?y
∴BE:EF=5:1.
则
∴PE=EF
BP=2PF=4EF,
所以BE=5EF
D
A
B
C
E
F
n
n
2k
解法2:
过点D作BF的平行线交AC于点Q,
y
k
Q
?y
2y
D
A
B
C
E
F
n
n
解法2:
过点D作BF的平行线交AC于点Q,
Q
2k
k
?y
2y
5y
y
∴BE:EF=5:1.
∴
D
A
B
C
E
F
2k
解法3:
过点E作BC的平行线交AC于点S,
S
n
n
k
?k
D
A
B
C
E
F
解法3:
过点E作BC的平行线交AC于点S,
S
n
n
?y
5y
y
2k
k
D
A
B
C
E
F
n
n
2k
解法4:
过点E作AC的平行线交BC于点T,
T
?k
?k
D
A
B
C
E
F
n
n
2k
解法4:
过点E作AC的平行线交BC于点T,
T
y
?y
5y
∵BD=2DC,
∴
∴BE:EF=5:1.
练习:
如图,D是△ABC的BC边上的点,
BD:DC=2:1,
求AF:CF的值.
D
A
B
C
E
F
E是AD的中点,
连结BE并延长交AC于F,
D
A
B
C
E
F
解法1:
过点D作CA的平行线交BF于点P,
P
n
n
2x
2x
2k
k
3x
AF:CF=2:3.
D
A
B
C
E
F
解法2:
过点D作BF的平行线交AC于点Q,
Q
n
n
2x
2x
2k
k
x
AF:CF=2:3.
D
A
B
C
E
F
解法3:
过点E作BC的平行线交AC于点S,
S
n
n
h
2h
4h
y
5y
4y
AF:CF=2:3.
D
A
B
C
E
F
解法4:
过点E作AC的平行线交BC于点T,
T
n
n
h
h
4h
5y
6y
4y
AF:CF=2:3.
拓展与提高
一直线截△ABC三边AB,AC,BC或其延长线于D,E,F,求证;
C
B
A
D
E
F
提示过A作BC的平行线交FD的延长线于G
A
B
C
D
F
E
G
H
P
拓展与提高
如图,大正方形的边长为2,小正方形的边长为1,那么CP∶PF=?
2∶3
