贵州省毕节市金沙五高2021-2022学年高二上学期第一次月考数学试题(Word版含答案解析)
文档属性
| 名称 | 贵州省毕节市金沙五高2021-2022学年高二上学期第一次月考数学试题(Word版含答案解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 934.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-29 00:00:00 | ||
图片预览

文档简介
毕节市金沙县第五中学2021-2022学年高二上学期第一次月考
数学
一、选择题(每小题5分,共12小题60分)
1.计算机执行下面的算法步骤后输出的结果是(
)
(1);(2);(3);(4);(5)输出y,x.
A.5,1
B.5,
C.1,5
D.,5
2.在30名运动员和6名教练员中用分层抽样的方法共抽取n人参加新闻发布会,若抽取的n人中教练员只有1人,则(
)
A.5
B.6
C.7
D.8
3.用系统抽样方法从编号为1,2,3,…,700的学生中抽样50人,若第2段中编号为20的学生被抽中,则第5段中被抽中的学生编号为(
)
A.48
B.62
C.76
D.90
4.下列给出的赋值语句正确的是(
)
A.
B.
C.
D.
5.如图是一算法的程序框图,若输出结果为,则在判断框中应填入的条件是(
)
A.
B.
C.
D.
6.《九章算术》是中国古代的数学专著,是《算经十书》中最重要的一本,成于公元1世纪左右,该书内容十分丰富,系统总结了战国、秦、汉时期的数学成就,其中第七章“盈不足”中有一道两鼠穿墙问题:今有垣厚五尺,两鼠对穿,大鼠日一尺,小鼠也日一尺,大鼠日自倍,小鼠日自半,问何日相逢?″题意是:“有两只老鼠从厚五尺墙的两边打洞穿墙,大老鼠第一天进一尺,以后每天加倍;小老鼠第一天也进一尺,以后每天减半.问几日两鼠相逢?”有人设计了如图所示的程序框图解决此问题,则此题的结果为(
)
A.2
B.3
C.4
D.5
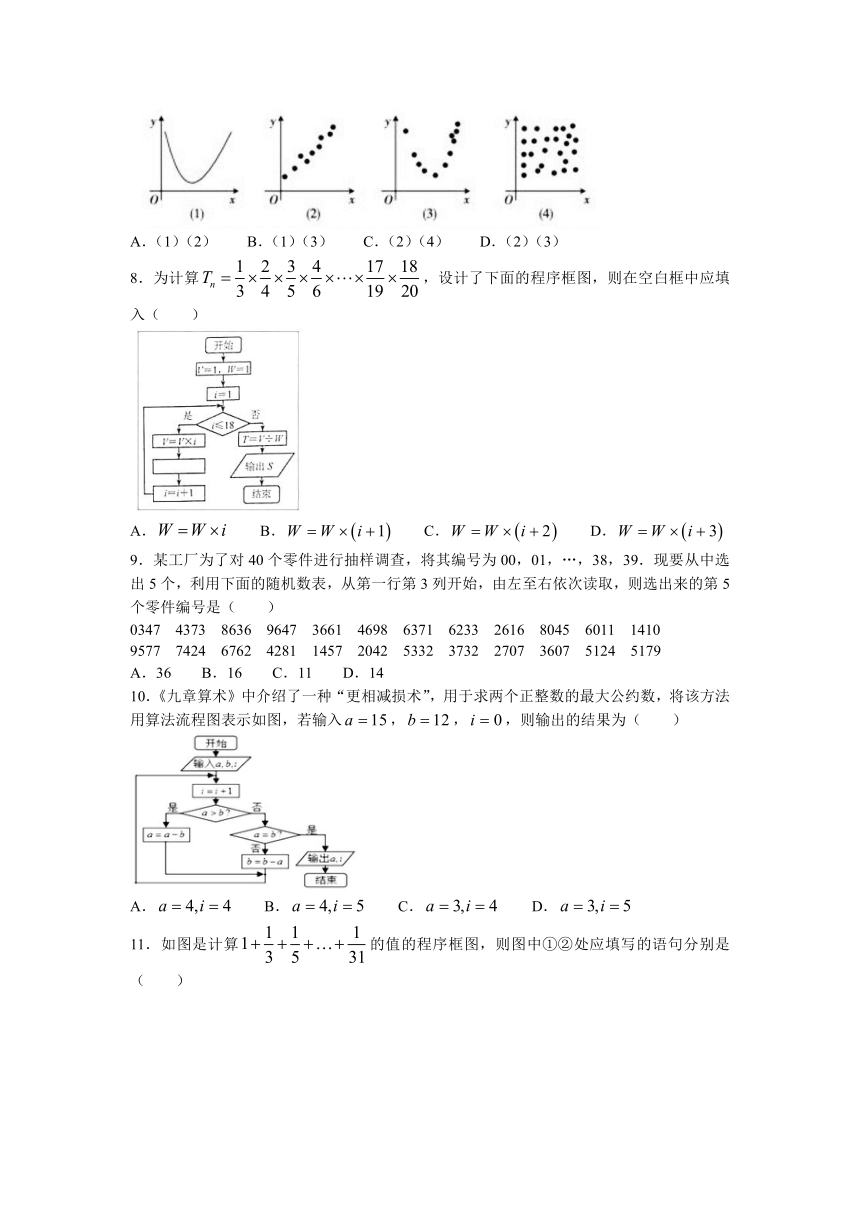
7.在下列各图中,两个变量具有相关关系的是(
)
A.(1)(2)
B.(1)(3)
C.(2)(4)
D.(2)(3)
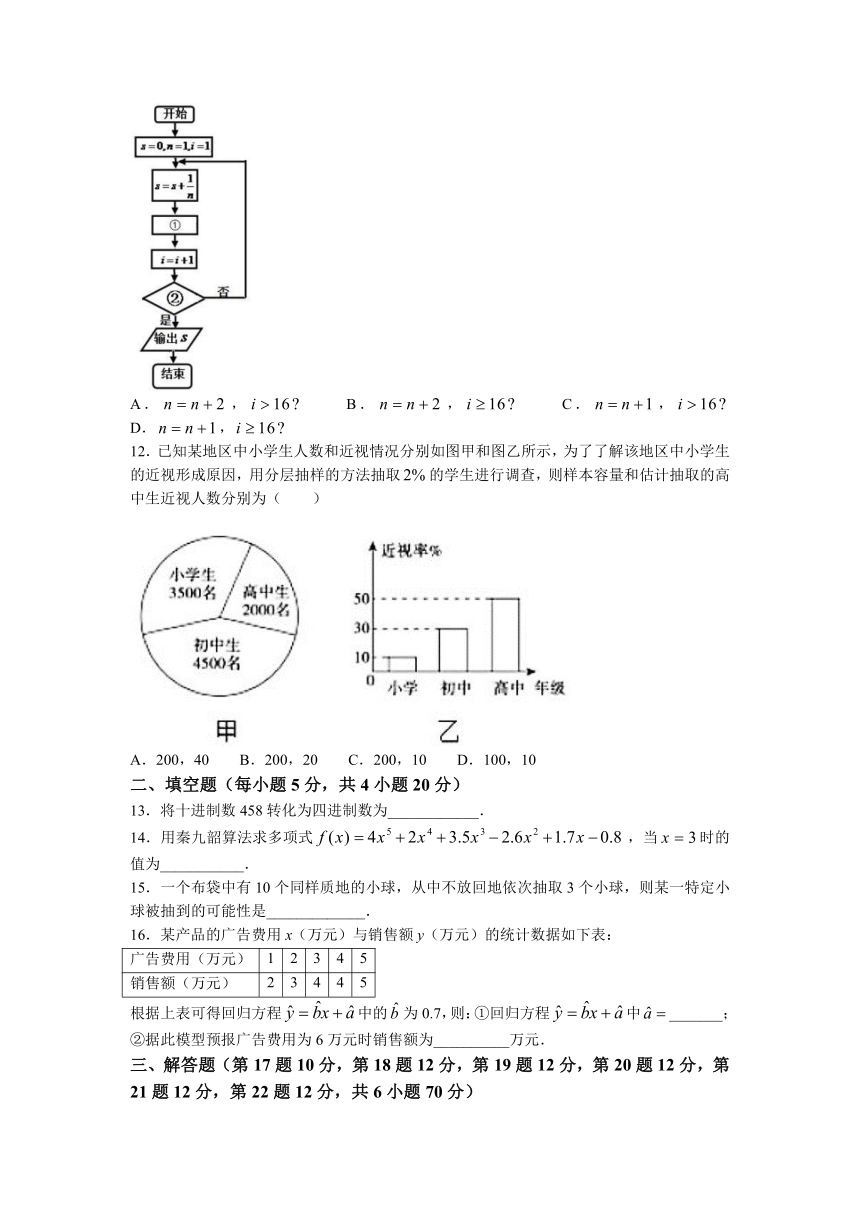
8.为计算,设计了下面的程序框图,则在空白框中应填入(
)
A.
B.
C.
D.
9.某工厂为了对40个零件进行抽样调查,将其编号为00,01,…,38,39.现要从中选出5个,利用下面的随机数表,从第一行第3列开始,由左至右依次读取,则选出来的第5个零件编号是(
)
0347
4373
8636
9647
3661
4698
6371
6233
2616
8045
6011
1410
9577
7424
6762
4281
1457
2042
5332
3732
2707
3607
5124
5179
A.36
B.16
C.11
D.14
10.《九章算术》中介绍了一种“更相减损术”,用于求两个正整数的最大公约数,将该方法用算法流程图表示如图,若输入,,,则输出的结果为(
)
A.
B.
C.
D.
11.如图是计算的值的程序框图,则图中①②处应填写的语句分别是(
)
A.,
B.,
C.,
D.,
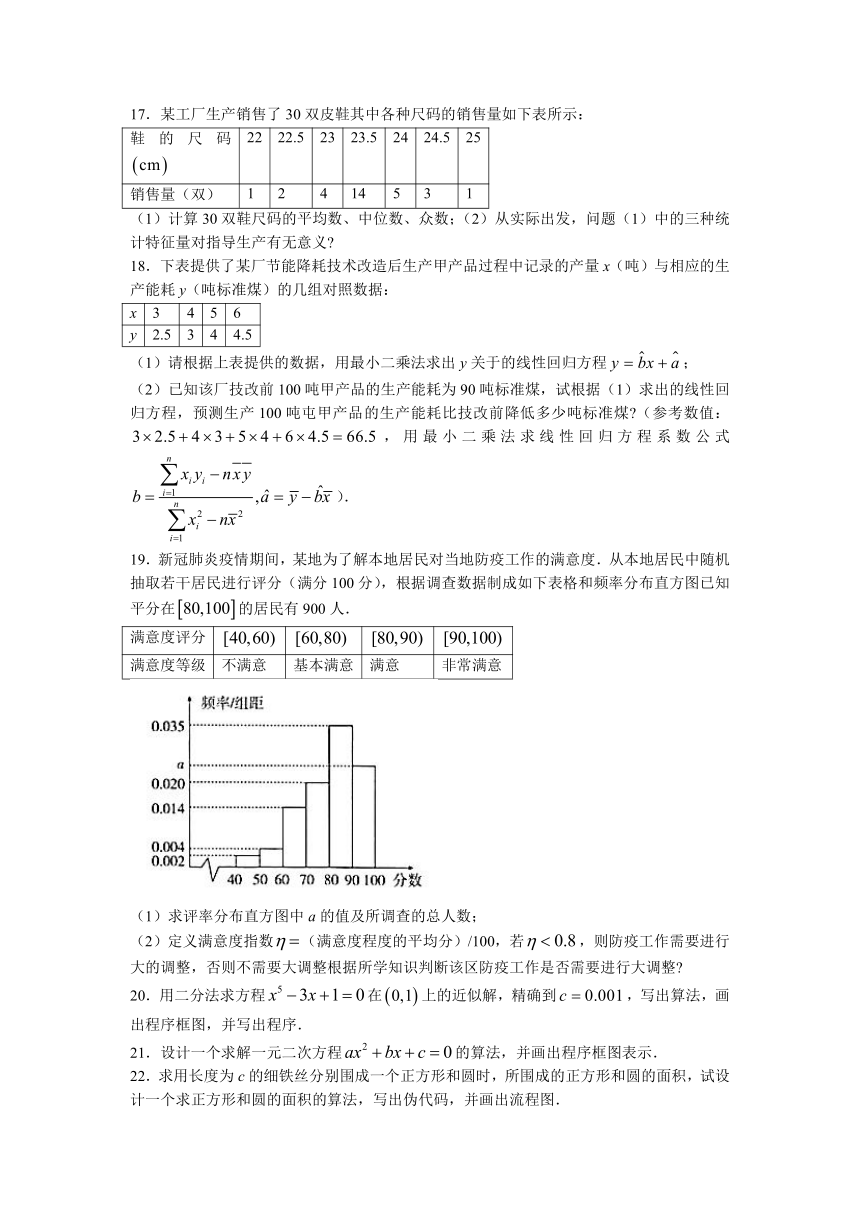
12.已知某地区中小学生人数和近视情况分别如图甲和图乙所示,为了了解该地区中小学生的近视形成原因,用分层抽样的方法抽取的学生进行调查,则样本容量和估计抽取的高中生近视人数分别为(
)
A.200,40
B.200,20
C.200,10
D.100,10
二、填空题(每小题5分,共4小题20分)
13.将十进制数458转化为四进制数为____________.
14.用秦九韶算法求多项式,当时的值为___________.
15.一个布袋中有10个同样质地的小球,从中不放回地依次抽取3个小球,则某一特定小球被抽到的可能性是_____________.
16.某产品的广告费用x(万元)与销售额y(万元)的统计数据如下表:
广告费用(万元)
1
2
3
4
5
销售额(万元)
2
3
4
4
5
根据上表可得回归方程中的为0.7,则:①回归方程中_______;②据此模型预报广告费用为6万元时销售额为__________万元.
三、解答题(第17题10分,第18题12分,第19题12分,第20题12分,第21题12分,第22题12分,共6小题70分)
17.某工厂生产销售了30双皮鞋其中各种尺码的销售量如下表所示:
鞋的尺码
22
22.5
23
23.5
24
24.5
25
销售量(双)
1
2
4
14
5
3
1
(1)计算30双鞋尺码的平均数、中位数、众数;(2)从实际出发,问题(1)中的三种统计特征量对指导生产有无意义?
18.下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据:
x
3
4
5
6
y
2.5
3
4
4.5
(1)请根据上表提供的数据,用最小二乘法求出y关于的线性回归方程;
(2)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤,试根据(1)求出的线性回归方程,预测生产100吨屯甲产品的生产能耗比技改前降低多少吨标准煤?(参考数值:,用最小二乘法求线性回归方程系数公式).
19.新冠肺炎疫情期间,某地为了解本地居民对当地防疫工作的满意度.从本地居民中随机抽取若干居民进行评分(满分100分),根据调查数据制成如下表格和频率分布直方图已知平分在的居民有900人.
满意度评分
满意度等级
不满意
基本满意
满意
非常满意
(1)求评率分布直方图中a的值及所调查的总人数;
(2)定义满意度指数(满意度程度的平均分)/100,若,则防疫工作需要进行大的调整,否则不需要大调整根据所学知识判断该区防疫工作是否需要进行大调整?
20.用二分法求方程在上的近似解,精确到,写出算法,画出程序框图,并写出程序.
21.设计一个求解一元二次方程的算法,并画出程序框图表示.
22.求用长度为c的细铁丝分别围成一个正方形和圆时,所围成的正方形和圆的面积,试设计一个求正方形和圆的面积的算法,写出伪代码,并画出流程图.
2021金沙五中月考答案和解析
第1题:
【答案】A
【解析】运行程序,,,,输出,.
第2题:
【答案】B
【解析】在30名运动员和6名教练员中用分层抽样的方法共抽取n人参加新闻发布会,若抽取的n人中教练员只有1人,则,求得,故选B.
第3题:
【答案】B
【解析】因为是从700名学生中抽出50名学生,组距是14,∵第2段中编号为20的学生被抽中,∴第5组抽取的为号.
第4题:
【答案】B
【解析】赋值语句可以对同一个变量进行重复赋值,的功能是把当前M的值取相反数后再赋给变量M.
第5题:
【答案】B
【解析】根据程序框图,运行结构如下:第一次循环,,第二次循环,,第三次循环,此时退出循环,故应填
第6题:
【答案】
【解析】初始值,,,,第一次循环,,,1,;第二次循环,,,,:第三次循环,,此时循环结束,输出,即第3日,两鼠相逢.
第7题:
【答案】D
【解析】若两个变量具有线性相关关系,那么在散点图中的点应位于某条直线的两侧附近,所以(2)正确,(3)中两变量具有非线性相关关系.故选D.
第8题:
【答案】C
【解析】根据式子的特征每个分式的分母比分子多2,即.
第9题:
【答案】C
【解析】从题中给的随机数表第一行第3列开始从左往右开始读取,重复的数字只读一次,读到的小于40的编号分别为36,33,26,16,11.
第10题:
【答案】D
【解析】模拟执行程序框图,输入
,,,,,,,,,
,,,,,,,,输出,.
第11题:
【答案】A
【解析】该程序是求数列的前16项和,①处变量n每次增加2,②处是循环控制条件,循环体共执行了16次,故时,退出循环.
第12题:
【答案】B
【解析】样本容量,估计抽取高中生近视人数为人.
第13题:
【答案】13022
【解析】所以这个数转为四进制数为13022(4).
第14题:
【答案】1209.4
【解析】多项式,将代入可得:.
第15题:
【答案】
【解析】因为在简单随机抽样过程中每个个体被抽到的可能性均为,所以某一特定小球被抽到的可能性为.
第16题:
【答案】1.5,5.7
【解析】∵回归方程中的为0.7,根据线性回归直线过样本中心点,,∴,则,解得,即回归方程为,据此模型预报广告费用为6万元时,销售额为.
第17题:
【答案】见解析
【解析】(1)30双皮鞋尺码的平均数为.又由于小于23.5的销售量为(双),大于的销售量为(双),故处于正中间位置的两个数均为,从而中位数为.又共出现14次,所以众数也为;(2)众数对厂家指导生产有实际意义,因为尺码为的鞋销量最好,厂家应多生产,而尺码为、的应少生产.
第18题:
【答案】(1);(2)19.65
【解析】(1)由系数公式可知,所以线性回归方程为.(2)当时,所以比改造前降低了19.65吨标准煤
第19题:
【答案】见解析
【解析】(1)由频率分布直方图知,即,解得,设总共调查了n人,则,解得,即调查的总人数为1500人;(2)有频率分布直方图知各段的频率分别为:0.02、0.04、0.14、0.20、0.35、0.25,所以,所以该区防疫工作不需要进行大调整.
第20题:
【答案】见解析
【解析】算法如下:第一步,取中点,将区间一分为二;第二步,若,则m就是方程的根;否则所求根在m的左侧或右侧;若,则,以m代替a;若,则,以m代替b;第三步,若,计算终止.此时,否则转到第一步.程序如下:
程序框图如下:
第21题:
【答案】见解析
【解析】算法步骤如下:第一步,输入3个系数a,b,c.第二步.计算.第三步,判断是否成立,若是,则计算,算;否则,输出“方程没有实数根”,结束算法.第四步.判断是否成立,若是,则输出;否则,计算,并输出,
程序框图:
第22题:
【答案】见解析.
【解析】流程图如图所示:
伪代码:
Read
c,
Print
数学
一、选择题(每小题5分,共12小题60分)
1.计算机执行下面的算法步骤后输出的结果是(
)
(1);(2);(3);(4);(5)输出y,x.
A.5,1
B.5,
C.1,5
D.,5
2.在30名运动员和6名教练员中用分层抽样的方法共抽取n人参加新闻发布会,若抽取的n人中教练员只有1人,则(
)
A.5
B.6
C.7
D.8
3.用系统抽样方法从编号为1,2,3,…,700的学生中抽样50人,若第2段中编号为20的学生被抽中,则第5段中被抽中的学生编号为(
)
A.48
B.62
C.76
D.90
4.下列给出的赋值语句正确的是(
)
A.
B.
C.
D.
5.如图是一算法的程序框图,若输出结果为,则在判断框中应填入的条件是(
)
A.
B.
C.
D.
6.《九章算术》是中国古代的数学专著,是《算经十书》中最重要的一本,成于公元1世纪左右,该书内容十分丰富,系统总结了战国、秦、汉时期的数学成就,其中第七章“盈不足”中有一道两鼠穿墙问题:今有垣厚五尺,两鼠对穿,大鼠日一尺,小鼠也日一尺,大鼠日自倍,小鼠日自半,问何日相逢?″题意是:“有两只老鼠从厚五尺墙的两边打洞穿墙,大老鼠第一天进一尺,以后每天加倍;小老鼠第一天也进一尺,以后每天减半.问几日两鼠相逢?”有人设计了如图所示的程序框图解决此问题,则此题的结果为(
)
A.2
B.3
C.4
D.5
7.在下列各图中,两个变量具有相关关系的是(
)
A.(1)(2)
B.(1)(3)
C.(2)(4)
D.(2)(3)
8.为计算,设计了下面的程序框图,则在空白框中应填入(
)
A.
B.
C.
D.
9.某工厂为了对40个零件进行抽样调查,将其编号为00,01,…,38,39.现要从中选出5个,利用下面的随机数表,从第一行第3列开始,由左至右依次读取,则选出来的第5个零件编号是(
)
0347
4373
8636
9647
3661
4698
6371
6233
2616
8045
6011
1410
9577
7424
6762
4281
1457
2042
5332
3732
2707
3607
5124
5179
A.36
B.16
C.11
D.14
10.《九章算术》中介绍了一种“更相减损术”,用于求两个正整数的最大公约数,将该方法用算法流程图表示如图,若输入,,,则输出的结果为(
)
A.
B.
C.
D.
11.如图是计算的值的程序框图,则图中①②处应填写的语句分别是(
)
A.,
B.,
C.,
D.,
12.已知某地区中小学生人数和近视情况分别如图甲和图乙所示,为了了解该地区中小学生的近视形成原因,用分层抽样的方法抽取的学生进行调查,则样本容量和估计抽取的高中生近视人数分别为(
)
A.200,40
B.200,20
C.200,10
D.100,10
二、填空题(每小题5分,共4小题20分)
13.将十进制数458转化为四进制数为____________.
14.用秦九韶算法求多项式,当时的值为___________.
15.一个布袋中有10个同样质地的小球,从中不放回地依次抽取3个小球,则某一特定小球被抽到的可能性是_____________.
16.某产品的广告费用x(万元)与销售额y(万元)的统计数据如下表:
广告费用(万元)
1
2
3
4
5
销售额(万元)
2
3
4
4
5
根据上表可得回归方程中的为0.7,则:①回归方程中_______;②据此模型预报广告费用为6万元时销售额为__________万元.
三、解答题(第17题10分,第18题12分,第19题12分,第20题12分,第21题12分,第22题12分,共6小题70分)
17.某工厂生产销售了30双皮鞋其中各种尺码的销售量如下表所示:
鞋的尺码
22
22.5
23
23.5
24
24.5
25
销售量(双)
1
2
4
14
5
3
1
(1)计算30双鞋尺码的平均数、中位数、众数;(2)从实际出发,问题(1)中的三种统计特征量对指导生产有无意义?
18.下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据:
x
3
4
5
6
y
2.5
3
4
4.5
(1)请根据上表提供的数据,用最小二乘法求出y关于的线性回归方程;
(2)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤,试根据(1)求出的线性回归方程,预测生产100吨屯甲产品的生产能耗比技改前降低多少吨标准煤?(参考数值:,用最小二乘法求线性回归方程系数公式).
19.新冠肺炎疫情期间,某地为了解本地居民对当地防疫工作的满意度.从本地居民中随机抽取若干居民进行评分(满分100分),根据调查数据制成如下表格和频率分布直方图已知平分在的居民有900人.
满意度评分
满意度等级
不满意
基本满意
满意
非常满意
(1)求评率分布直方图中a的值及所调查的总人数;
(2)定义满意度指数(满意度程度的平均分)/100,若,则防疫工作需要进行大的调整,否则不需要大调整根据所学知识判断该区防疫工作是否需要进行大调整?
20.用二分法求方程在上的近似解,精确到,写出算法,画出程序框图,并写出程序.
21.设计一个求解一元二次方程的算法,并画出程序框图表示.
22.求用长度为c的细铁丝分别围成一个正方形和圆时,所围成的正方形和圆的面积,试设计一个求正方形和圆的面积的算法,写出伪代码,并画出流程图.
2021金沙五中月考答案和解析
第1题:
【答案】A
【解析】运行程序,,,,输出,.
第2题:
【答案】B
【解析】在30名运动员和6名教练员中用分层抽样的方法共抽取n人参加新闻发布会,若抽取的n人中教练员只有1人,则,求得,故选B.
第3题:
【答案】B
【解析】因为是从700名学生中抽出50名学生,组距是14,∵第2段中编号为20的学生被抽中,∴第5组抽取的为号.
第4题:
【答案】B
【解析】赋值语句可以对同一个变量进行重复赋值,的功能是把当前M的值取相反数后再赋给变量M.
第5题:
【答案】B
【解析】根据程序框图,运行结构如下:第一次循环,,第二次循环,,第三次循环,此时退出循环,故应填
第6题:
【答案】
【解析】初始值,,,,第一次循环,,,1,;第二次循环,,,,:第三次循环,,此时循环结束,输出,即第3日,两鼠相逢.
第7题:
【答案】D
【解析】若两个变量具有线性相关关系,那么在散点图中的点应位于某条直线的两侧附近,所以(2)正确,(3)中两变量具有非线性相关关系.故选D.
第8题:
【答案】C
【解析】根据式子的特征每个分式的分母比分子多2,即.
第9题:
【答案】C
【解析】从题中给的随机数表第一行第3列开始从左往右开始读取,重复的数字只读一次,读到的小于40的编号分别为36,33,26,16,11.
第10题:
【答案】D
【解析】模拟执行程序框图,输入
,,,,,,,,,
,,,,,,,,输出,.
第11题:
【答案】A
【解析】该程序是求数列的前16项和,①处变量n每次增加2,②处是循环控制条件,循环体共执行了16次,故时,退出循环.
第12题:
【答案】B
【解析】样本容量,估计抽取高中生近视人数为人.
第13题:
【答案】13022
【解析】所以这个数转为四进制数为13022(4).
第14题:
【答案】1209.4
【解析】多项式,将代入可得:.
第15题:
【答案】
【解析】因为在简单随机抽样过程中每个个体被抽到的可能性均为,所以某一特定小球被抽到的可能性为.
第16题:
【答案】1.5,5.7
【解析】∵回归方程中的为0.7,根据线性回归直线过样本中心点,,∴,则,解得,即回归方程为,据此模型预报广告费用为6万元时,销售额为.
第17题:
【答案】见解析
【解析】(1)30双皮鞋尺码的平均数为.又由于小于23.5的销售量为(双),大于的销售量为(双),故处于正中间位置的两个数均为,从而中位数为.又共出现14次,所以众数也为;(2)众数对厂家指导生产有实际意义,因为尺码为的鞋销量最好,厂家应多生产,而尺码为、的应少生产.
第18题:
【答案】(1);(2)19.65
【解析】(1)由系数公式可知,所以线性回归方程为.(2)当时,所以比改造前降低了19.65吨标准煤
第19题:
【答案】见解析
【解析】(1)由频率分布直方图知,即,解得,设总共调查了n人,则,解得,即调查的总人数为1500人;(2)有频率分布直方图知各段的频率分别为:0.02、0.04、0.14、0.20、0.35、0.25,所以,所以该区防疫工作不需要进行大调整.
第20题:
【答案】见解析
【解析】算法如下:第一步,取中点,将区间一分为二;第二步,若,则m就是方程的根;否则所求根在m的左侧或右侧;若,则,以m代替a;若,则,以m代替b;第三步,若,计算终止.此时,否则转到第一步.程序如下:
程序框图如下:
第21题:
【答案】见解析
【解析】算法步骤如下:第一步,输入3个系数a,b,c.第二步.计算.第三步,判断是否成立,若是,则计算,算;否则,输出“方程没有实数根”,结束算法.第四步.判断是否成立,若是,则输出;否则,计算,并输出,
程序框图:
第22题:
【答案】见解析.
【解析】流程图如图所示:
伪代码:
Read
c,
同课章节目录
