河南省信阳市息县第一重点高中2022届高三上学期9月质量检测数学试题(Word版含答案)
文档属性
| 名称 | 河南省信阳市息县第一重点高中2022届高三上学期9月质量检测数学试题(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 770.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-29 15:59:12 | ||
图片预览



文档简介
息县第一高级中学2022届高三上学期9月质量检测
文科数学
一?选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.
设命题,则(
)
A.
B.
C.
D.
2.
已知集合,则(
)
A.
B.
C.
D.
3.
函数的定义域是(
)
A.
B.
C.
D.
4.
“x
+
y
>2”是“x
>1且y
>1”的
A.
充分不必要条件
B.
必要不充分条件
C
充要条件
D.
既不充分也不必要条件
5.
已知命题,命题,则下列命题为真命题的是(
)
A.
B.
C.
D.
6.
若,则下列结论正确的是(
)
A.
B.
C.
D.
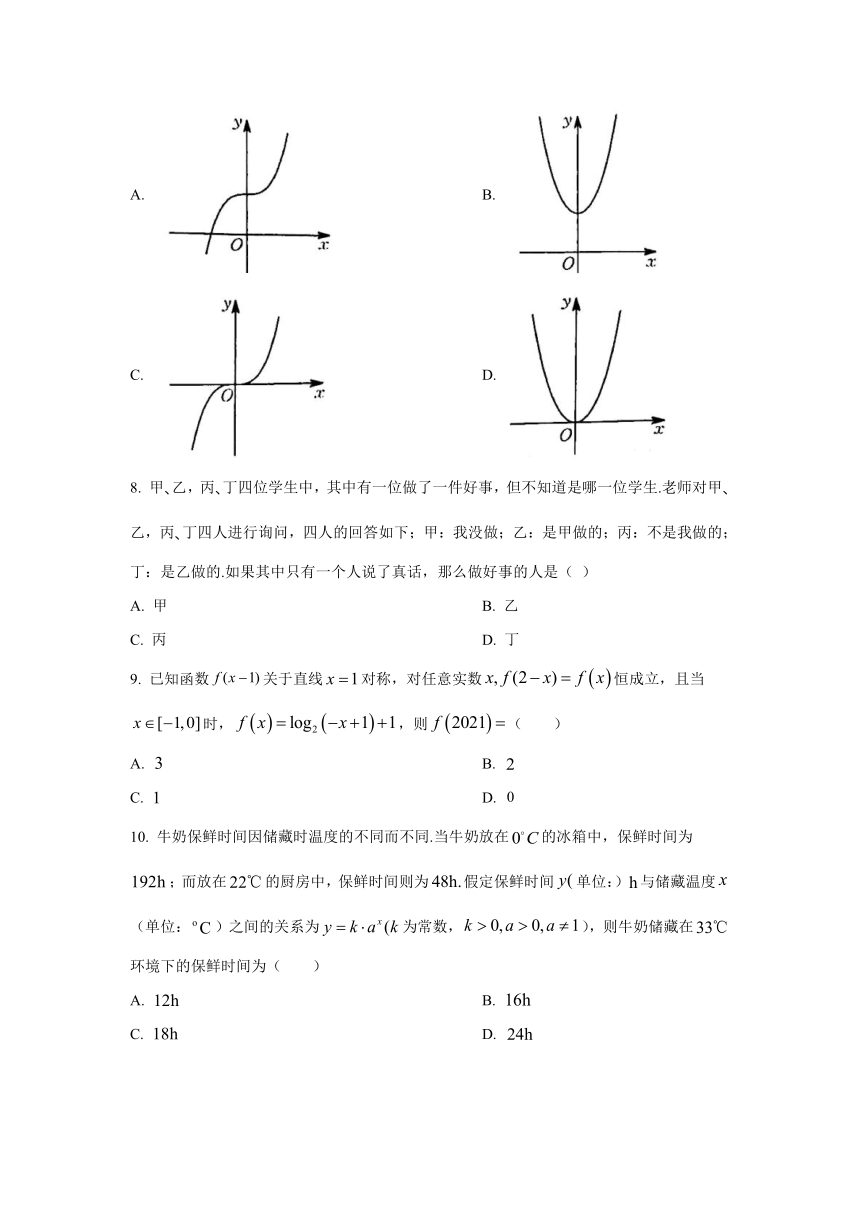
7.
函数的图象大致是(
)
A.
B.
C.
D.
8.
甲?乙,丙?丁四位学生中,其中有一位做了一件好事,但不知道是哪一位学生.老师对甲?乙,丙?丁四人进行询问,四人的回答如下;甲:我没做;乙:是甲做的;丙:不是我做的;丁:是乙做的.如果其中只有一个人说了真话,那么做好事的人是(
)
A.
甲
B.
乙
C.
丙
D.
丁
9.
已知函数关于直线对称,对任意实数恒成立,且当时,,则(
)
A.
B.
C.
D.
10.
牛奶保鲜时间因储藏时温度的不同而不同.当牛奶放在的冰箱中,保鲜时间为;而放在的厨房中,保鲜时间则为假定保鲜时间单位:)与储藏温度(单位:)之间的关系为为常数,),则牛奶储藏在环境下的保鲜时间为(
)
A.
B.
C.
D.
11.
已知函数若关于的方程恰有三个不同的实数解,则实数的取值范围是(
)
A.
B.
C.
D.
12.
已知定义在的函数满足:,其中为的导函数,则不等式的解集为(
)
A.
B.
C.
D.
二?填空题(每题5分,满分20分,将答案填在答题纸上)
13.
___________.
14.
已知函数,则曲线在处的切线方程为___________.
15.
若定义在上的函数满足:①对于任意的,都有;②为奇函数.则函数的一个解析式可以是___________.
16.
已知是上的以为周期的奇函数,则___________,___________.
三?解答题(共70分.解答应写出文字说明?证明过程或演算步骤.)
17.
已知集合.
(1)若,求;
(2)若,求实数的取值范围.
18.
已知函数有零点;.
(1)若为真,求实数的取值范围;
(2)若为真,为假,求实数的取值范围.
19.
已知函数.
(1)若函数的值域为,求实数的取值范围;
(2)若存在,使得成立,求实数取值范围.
20
已知函数.
(1)当时,求函数的单调区间;
(2)若函数存在一个极大值点和一个极小值点,则是否存在实数使得成立?若成立,求出的值;若不成立,请说明理由.
21.
2021年新冠肺炎仍在世界好多国家肆虐,并且出现了传染性更强“德尔塔”变异毒株?“拉姆达”变异毒株,尽管我国抗疫取得了很大的成绩,疫情也得到了很好的遏制,但由于整个国际环境的影响,时而也会出现一些散发病例,故而抗疫形势依然艰巨,日常防护依然不能有丝毫放松.在日常防护中,口罩是必不可少的防护用品.某口罩生产厂家为保障抗疫需求,调整了口罩生产规模.已知该厂生产口罩的固定成本为万元,每生产万箱,需另投入成本万元,当年产量不足万箱时,;当年产量不低于万箱时,若每万箱口罩售价万元,通过市场分析,该口罩厂生产的口罩当年可以全部销售完.
(1)求年利润(万元)关于年产量(万箱)的函数关系式;
(2)年产量为多少万箱时,该口罩生产厂家所获得年利润最大?(注:)
22.
已知函数.
(1)当时,求证:;
(2)若有两个零点,求的取值范围.
息县第一高级中学2022届高三上学期9月质量检测
文科数学
答案版
一?选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.
设命题,则(
)
A.
B.
C.
D.
答案:D
2.
已知集合,则(
)
A.
B.
C.
D.
答案:B
3.
函数的定义域是(
)
A.
B.
C.
D.
答案:C
4.
“x
+
y
>2”是“x
>1且y
>1”的
A.
充分不必要条件
B.
必要不充分条件
C
充要条件
D.
既不充分也不必要条件
答案:B
5.
已知命题,命题,则下列命题为真命题的是(
)
A.
B.
C.
D.
答案:C
6.
若,则下列结论正确的是(
)
A.
B.
C.
D.
答案:C
7.
函数的图象大致是(
)
A.
B.
C.
D.
答案:D
8.
甲?乙,丙?丁四位学生中,其中有一位做了一件好事,但不知道是哪一位学生.老师对甲?乙,丙?丁四人进行询问,四人的回答如下;甲:我没做;乙:是甲做的;丙:不是我做的;丁:是乙做的.如果其中只有一个人说了真话,那么做好事的人是(
)
A.
甲
B.
乙
C.
丙
D.
丁
答案:C
9.
已知函数关于直线对称,对任意实数恒成立,且当时,,则(
)
A.
B.
C.
D.
答案:B
10.
牛奶保鲜时间因储藏时温度的不同而不同.当牛奶放在的冰箱中,保鲜时间为;而放在的厨房中,保鲜时间则为假定保鲜时间单位:)与储藏温度(单位:)之间的关系为为常数,),则牛奶储藏在环境下的保鲜时间为(
)
A.
B.
C.
D.
答案:D
11.
已知函数若关于的方程恰有三个不同的实数解,则实数的取值范围是(
)
A.
B.
C.
D.
答案:C
12.
已知定义在的函数满足:,其中为的导函数,则不等式的解集为(
)
A.
B.
C.
D.
答案:A
二?填空题(每题5分,满分20分,将答案填在答题纸上)
13.
___________.
答案:
14.
已知函数,则曲线在处的切线方程为___________.
答案:
15.
若定义在上的函数满足:①对于任意的,都有;②为奇函数.则函数的一个解析式可以是___________.
答案:(答案不唯一)
16.
已知是上的以为周期的奇函数,则___________,___________.
答案:
①.
②.
三?解答题(共70分.解答应写出文字说明?证明过程或演算步骤.)
17.
已知集合.
(1)若,求;
(2)若,求实数的取值范围.
答案:(1)或;(2).
18.
已知函数有零点;.
(1)若为真,求实数的取值范围;
(2)若为真,为假,求实数的取值范围.
答案:(1);(2).
19.
已知函数.
(1)若函数的值域为,求实数的取值范围;
(2)若存在,使得成立,求实数取值范围.
答案:(1);(2).
20
已知函数.
(1)当时,求函数的单调区间;
(2)若函数存在一个极大值点和一个极小值点,则是否存在实数使得成立?若成立,求出的值;若不成立,请说明理由.
答案:(1)递增区间为和,递减区间为;(2)不存在,理由见解析.
21.
2021年新冠肺炎仍在世界好多国家肆虐,并且出现了传染性更强“德尔塔”变异毒株?“拉姆达”变异毒株,尽管我国抗疫取得了很大的成绩,疫情也得到了很好的遏制,但由于整个国际环境的影响,时而也会出现一些散发病例,故而抗疫形势依然艰巨,日常防护依然不能有丝毫放松.在日常防护中,口罩是必不可少的防护用品.某口罩生产厂家为保障抗疫需求,调整了口罩生产规模.已知该厂生产口罩的固定成本为万元,每生产万箱,需另投入成本万元,当年产量不足万箱时,;当年产量不低于万箱时,若每万箱口罩售价万元,通过市场分析,该口罩厂生产的口罩当年可以全部销售完.
(1)求年利润(万元)关于年产量(万箱)的函数关系式;
(2)年产量为多少万箱时,该口罩生产厂家所获得年利润最大?(注:)
答案:(1);(2)年产量为万箱.
22.
已知函数.
(1)当时,求证:;
(2)若有两个零点,求的取值范围.
答案:(1)证明见解析;(2).
文科数学
一?选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.
设命题,则(
)
A.
B.
C.
D.
2.
已知集合,则(
)
A.
B.
C.
D.
3.
函数的定义域是(
)
A.
B.
C.
D.
4.
“x
+
y
>2”是“x
>1且y
>1”的
A.
充分不必要条件
B.
必要不充分条件
C
充要条件
D.
既不充分也不必要条件
5.
已知命题,命题,则下列命题为真命题的是(
)
A.
B.
C.
D.
6.
若,则下列结论正确的是(
)
A.
B.
C.
D.
7.
函数的图象大致是(
)
A.
B.
C.
D.
8.
甲?乙,丙?丁四位学生中,其中有一位做了一件好事,但不知道是哪一位学生.老师对甲?乙,丙?丁四人进行询问,四人的回答如下;甲:我没做;乙:是甲做的;丙:不是我做的;丁:是乙做的.如果其中只有一个人说了真话,那么做好事的人是(
)
A.
甲
B.
乙
C.
丙
D.
丁
9.
已知函数关于直线对称,对任意实数恒成立,且当时,,则(
)
A.
B.
C.
D.
10.
牛奶保鲜时间因储藏时温度的不同而不同.当牛奶放在的冰箱中,保鲜时间为;而放在的厨房中,保鲜时间则为假定保鲜时间单位:)与储藏温度(单位:)之间的关系为为常数,),则牛奶储藏在环境下的保鲜时间为(
)
A.
B.
C.
D.
11.
已知函数若关于的方程恰有三个不同的实数解,则实数的取值范围是(
)
A.
B.
C.
D.
12.
已知定义在的函数满足:,其中为的导函数,则不等式的解集为(
)
A.
B.
C.
D.
二?填空题(每题5分,满分20分,将答案填在答题纸上)
13.
___________.
14.
已知函数,则曲线在处的切线方程为___________.
15.
若定义在上的函数满足:①对于任意的,都有;②为奇函数.则函数的一个解析式可以是___________.
16.
已知是上的以为周期的奇函数,则___________,___________.
三?解答题(共70分.解答应写出文字说明?证明过程或演算步骤.)
17.
已知集合.
(1)若,求;
(2)若,求实数的取值范围.
18.
已知函数有零点;.
(1)若为真,求实数的取值范围;
(2)若为真,为假,求实数的取值范围.
19.
已知函数.
(1)若函数的值域为,求实数的取值范围;
(2)若存在,使得成立,求实数取值范围.
20
已知函数.
(1)当时,求函数的单调区间;
(2)若函数存在一个极大值点和一个极小值点,则是否存在实数使得成立?若成立,求出的值;若不成立,请说明理由.
21.
2021年新冠肺炎仍在世界好多国家肆虐,并且出现了传染性更强“德尔塔”变异毒株?“拉姆达”变异毒株,尽管我国抗疫取得了很大的成绩,疫情也得到了很好的遏制,但由于整个国际环境的影响,时而也会出现一些散发病例,故而抗疫形势依然艰巨,日常防护依然不能有丝毫放松.在日常防护中,口罩是必不可少的防护用品.某口罩生产厂家为保障抗疫需求,调整了口罩生产规模.已知该厂生产口罩的固定成本为万元,每生产万箱,需另投入成本万元,当年产量不足万箱时,;当年产量不低于万箱时,若每万箱口罩售价万元,通过市场分析,该口罩厂生产的口罩当年可以全部销售完.
(1)求年利润(万元)关于年产量(万箱)的函数关系式;
(2)年产量为多少万箱时,该口罩生产厂家所获得年利润最大?(注:)
22.
已知函数.
(1)当时,求证:;
(2)若有两个零点,求的取值范围.
息县第一高级中学2022届高三上学期9月质量检测
文科数学
答案版
一?选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.
设命题,则(
)
A.
B.
C.
D.
答案:D
2.
已知集合,则(
)
A.
B.
C.
D.
答案:B
3.
函数的定义域是(
)
A.
B.
C.
D.
答案:C
4.
“x
+
y
>2”是“x
>1且y
>1”的
A.
充分不必要条件
B.
必要不充分条件
C
充要条件
D.
既不充分也不必要条件
答案:B
5.
已知命题,命题,则下列命题为真命题的是(
)
A.
B.
C.
D.
答案:C
6.
若,则下列结论正确的是(
)
A.
B.
C.
D.
答案:C
7.
函数的图象大致是(
)
A.
B.
C.
D.
答案:D
8.
甲?乙,丙?丁四位学生中,其中有一位做了一件好事,但不知道是哪一位学生.老师对甲?乙,丙?丁四人进行询问,四人的回答如下;甲:我没做;乙:是甲做的;丙:不是我做的;丁:是乙做的.如果其中只有一个人说了真话,那么做好事的人是(
)
A.
甲
B.
乙
C.
丙
D.
丁
答案:C
9.
已知函数关于直线对称,对任意实数恒成立,且当时,,则(
)
A.
B.
C.
D.
答案:B
10.
牛奶保鲜时间因储藏时温度的不同而不同.当牛奶放在的冰箱中,保鲜时间为;而放在的厨房中,保鲜时间则为假定保鲜时间单位:)与储藏温度(单位:)之间的关系为为常数,),则牛奶储藏在环境下的保鲜时间为(
)
A.
B.
C.
D.
答案:D
11.
已知函数若关于的方程恰有三个不同的实数解,则实数的取值范围是(
)
A.
B.
C.
D.
答案:C
12.
已知定义在的函数满足:,其中为的导函数,则不等式的解集为(
)
A.
B.
C.
D.
答案:A
二?填空题(每题5分,满分20分,将答案填在答题纸上)
13.
___________.
答案:
14.
已知函数,则曲线在处的切线方程为___________.
答案:
15.
若定义在上的函数满足:①对于任意的,都有;②为奇函数.则函数的一个解析式可以是___________.
答案:(答案不唯一)
16.
已知是上的以为周期的奇函数,则___________,___________.
答案:
①.
②.
三?解答题(共70分.解答应写出文字说明?证明过程或演算步骤.)
17.
已知集合.
(1)若,求;
(2)若,求实数的取值范围.
答案:(1)或;(2).
18.
已知函数有零点;.
(1)若为真,求实数的取值范围;
(2)若为真,为假,求实数的取值范围.
答案:(1);(2).
19.
已知函数.
(1)若函数的值域为,求实数的取值范围;
(2)若存在,使得成立,求实数取值范围.
答案:(1);(2).
20
已知函数.
(1)当时,求函数的单调区间;
(2)若函数存在一个极大值点和一个极小值点,则是否存在实数使得成立?若成立,求出的值;若不成立,请说明理由.
答案:(1)递增区间为和,递减区间为;(2)不存在,理由见解析.
21.
2021年新冠肺炎仍在世界好多国家肆虐,并且出现了传染性更强“德尔塔”变异毒株?“拉姆达”变异毒株,尽管我国抗疫取得了很大的成绩,疫情也得到了很好的遏制,但由于整个国际环境的影响,时而也会出现一些散发病例,故而抗疫形势依然艰巨,日常防护依然不能有丝毫放松.在日常防护中,口罩是必不可少的防护用品.某口罩生产厂家为保障抗疫需求,调整了口罩生产规模.已知该厂生产口罩的固定成本为万元,每生产万箱,需另投入成本万元,当年产量不足万箱时,;当年产量不低于万箱时,若每万箱口罩售价万元,通过市场分析,该口罩厂生产的口罩当年可以全部销售完.
(1)求年利润(万元)关于年产量(万箱)的函数关系式;
(2)年产量为多少万箱时,该口罩生产厂家所获得年利润最大?(注:)
答案:(1);(2)年产量为万箱.
22.
已知函数.
(1)当时,求证:;
(2)若有两个零点,求的取值范围.
答案:(1)证明见解析;(2).
同课章节目录
