3.1.1函数的概念 课件(共30张PPT)
文档属性
| 名称 | 3.1.1函数的概念 课件(共30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-29 00:00:00 | ||
图片预览








文档简介
(共30张PPT)
3.1.1函数的概念
2019人教版A
必修一
新知导入
身边处处有函数
S=350t
这里,t和S是两个变量,而且对于t的每一个确定的值,S都有唯一确定的值
在初中我们初步学习过一些函数:回顾一下,我们在初中学习过哪些函数呢?
初中学过的函数
1、一次函数:
2、二次函数:
3、反比例函数:
4、正比例函数:
有两个变量x,y,变量y随着变量x的变化而变化
新知导入
初中函数的定义
新知导入
在变化过程中,有两个变量x和y,
如果给定一个x值,
相应地就确定了一个y值,
那么我们称
y是
x的函数.
其中
x是自变量,y是因变量.
新知讲解
我们来研究前面给出的例子
A1={t|0≤t≤0.5}
B1={S|0≤S≤175}
问题2.某公司要求工人每周工作至少1天,至多不超过6天.工资标准是每人每
天350元,而且每周付一次工资,工资y与一周工作天数x的关系可以表示为:
y=350x
A2={1,2,3,4,5,6}
B2={350,700,1050,1400,1750,2100}
y=350x
A1={t|0≤t≤0.5}
B1={S|0≤S≤175}
在S=350t
作用下,A1到B1存在的对应关系
A2={1,2,3,4,5,6}
B2={350,700,1050,1400,1750,2100}
每一个t
唯一一个S
对应
每一个x
对应
唯一一个y
对应
新知讲解
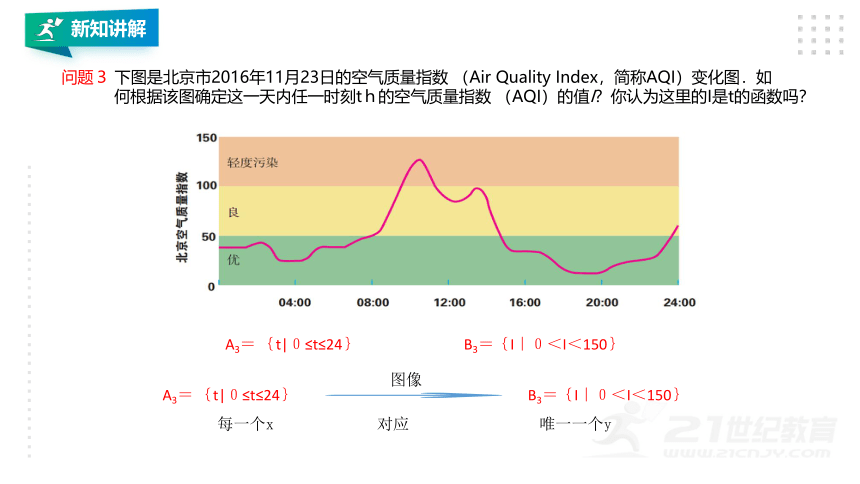
问题3
下图是北京市2016年11月23日的空气质量指数
(Air
Quality
Index,简称AQI)变化图.如
何根据该图确定这一天内任一时刻th的空气质量指数
(AQI)的值I?你认为这里的I是t的函数吗?
A3=
{t|0≤t≤24}
B3={I|0<I<150}
A3=
{t|0≤t≤24}
B3={I|0<I<150}
图像
每一个x
对应
唯一一个y
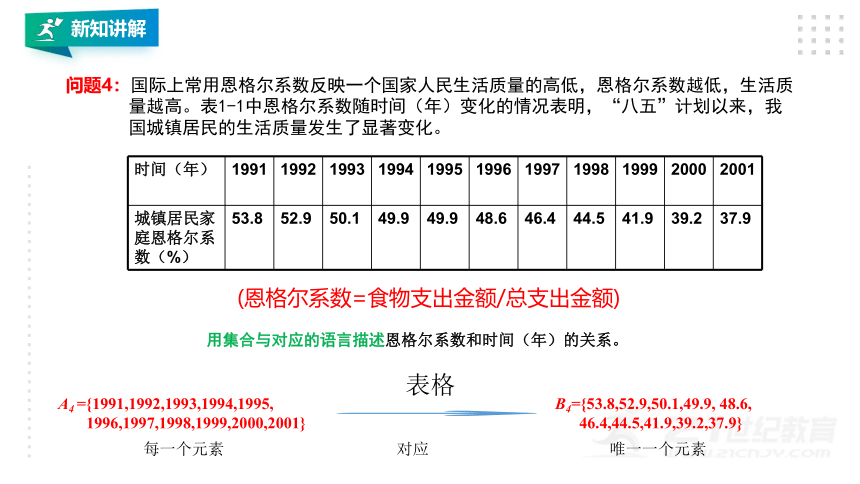
问题4:国际上常用恩格尔系数反映一个国家人民生活质量的高低,恩格尔系数越低,生活质
量越高。表1-1中恩格尔系数随时间(年)变化的情况表明,“八五”计划以来,我
国城镇居民的生活质量发生了显著变化。
时间(年)
1991
1992
1993
1994
1995
1996
1997
1998
1999
2000
2001
城镇居民家庭恩格尔系数(%)
53.8
52.9
50.1
49.9
49.9
48.6
46.4
44.5
41.9
39.2
37.9
(恩格尔系数=食物支出金额/总支出金额)
A4
={1991,1992,1993,1994,1995,
1996,1997,1998,1999,2000,2001}
B4={53.8,52.9,50.1,49.9,
48.6,
46.4,44.5,41.9,39.2,37.9}
表格
用集合与对应的语言描述恩格尔系数和时间(年)的关系。
新知讲解
每一个元素
唯一一个元素
对应
上述问题的共同特征有:
(1)都包含两个非空数集,用A,B来表示;
(2)都有一个对应关系;
(3)尽管对应关系的表示方法不同,但它们都有如下特性:对于数集A中的任意一
个数x,按照对应关系,在数集B中都有唯一确定的数y和它对应.
新知讲解
设A、B是非空数集,如果按照某种确定的对应关系
f,使对于集合A中的任意一
个数
x,在集合B中都有唯一确定的数
f(x)
和它对应,就称f:
A→B
为从集合A到集合
B的一个函数,记作:
y=f(x)
,
x∈A
x叫作自变量,集合A叫作函数的定义域,集合{f(x)|x∈A}
叫作函数的值域.
注意:(1)A、B为数集且非空;(2)值域{f(x)|x∈A}
是集合B的一个子集,不一定就是
集合B。(3)强调A中的每一个元素,在B中有且唯一元素对应,既不能没有对应,
也不能多一个,而是恰好一个。
函数的三要素:
定义域
对应关系
值域
新知讲解
新知讲解
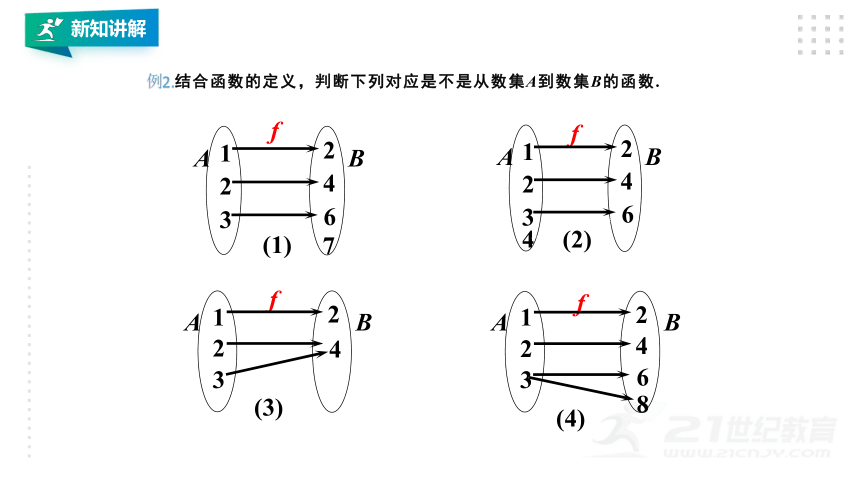
例2.结合函数的定义,判断下列对应是不是从数集A到数集B的函数.
A
B
f
1
2
2
4
3
6
7
A
B
f
1
2
2
4
3
6
4
A
B
f
1
2
2
4
3
B
A
f
1
2
2
4
3
6
8
(2)
(3)
(4)
(1)
新知讲解
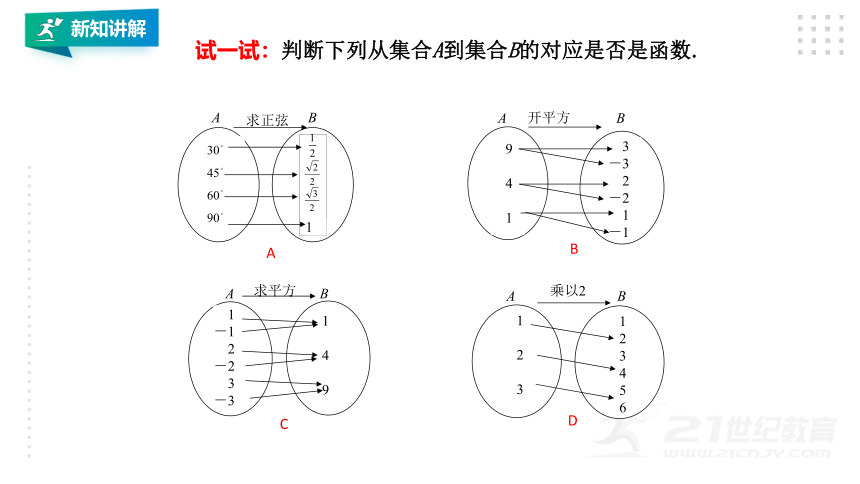
试一试:判断下列从集合A到集合B的对应是否是函数.
A
B
C
D
新知讲解
下列图形哪个可以表示函数的图象?
A
B
C
D
0
x
y
F
0
x
y
C
0
x
y
E
判断下列对应能否表示y是x的函数
分析:(1)中,任意一个x的值,都有唯一一个y值对应,表示y是x的函数。
(2)中,当x=1时,则y=1或y=-1;即一个x
有二个y值对应,所以不表示函数。
合作探究
初中学过函数的定义域和值域
反比例函数
一次函数
二次函数
a
>
0
a
<
0
图像
定义域
值域
合作探究
试一试:求下列函数的定义域
(1)
函数
f(x)=2x-3
的定义域是?
R
(2)
函数
的定义域是?
(3)
函数
的定义域是?
(4)
函数
的定义域是?
新知讲解
区间的概念
区间的几何表示:在数轴表示时,用实心点表示包括在区间内的端点,用空心点表示不包括在区间内的端点.
实数集R可以用区间表示为(-∞,+∞),“∞”读作
“无穷大”,
“-∞”读作
“负无穷大”,“+∞”读作
“正无穷大”.
新知讲解
新知讲解
我们可以把满足x≥a,x>a,x≤b,x<b的实数x的集合,用区间
分别表示为[a,+∞),(a,+∞),(-∞,b],(-∞,b)
合作探究
合作探究
合作探究
合作探究
课堂练习
试一试:
用区间表示下列集合
1.{x|1≤x≤4}
2.{x|-13.{x|1≤x<5}
4.{x|x[1,4]
(-1,2]
[1,5)
(-∞,b)
课堂练习
试一试:练习课本P67
1.求下列函数的定义域(用区间表示):
f(2)=32
f(-2)=-32
f(2)+f(-2)=0
f(a)=3a3+2a
f(-a)=-3a3-2a
f(a)+f(-a)=0
答:(1)不是同一个函数。因为定义域不同
答:(2)不是同一函数,因为g(x)中x≠0,所以定义域不同,故不是同一函数.
课堂总结
1.理解函数的定义,从数集到数集的一一对应关系.
2.根据函数的定义,判断是否是函数及相同函数.
3.求函数的定义域,区间的概念及用区间表示集合.
4.了解构成函数的三要素;
板书设计
函数的定义
设A、B是非空数集,如果按照
某种确定的对应关系
f,使对于集
合A中的任意一个数
x,在集合B中
都有唯一确定的数
f(x)
和它对应,
就称f:
A→B
为从集合A到集合
B的一个函数,记作:
y=f(x)
,
x∈A
区间的概念
作业布置
一、举出几个(三个以上)函数的实际例子,并写出其定义域和值域。
二、课本P721、2、3、4
;
P736、9
https://www.21cnjy.com/help/help_extract.php
3.1.1函数的概念
2019人教版A
必修一
新知导入
身边处处有函数
S=350t
这里,t和S是两个变量,而且对于t的每一个确定的值,S都有唯一确定的值
在初中我们初步学习过一些函数:回顾一下,我们在初中学习过哪些函数呢?
初中学过的函数
1、一次函数:
2、二次函数:
3、反比例函数:
4、正比例函数:
有两个变量x,y,变量y随着变量x的变化而变化
新知导入
初中函数的定义
新知导入
在变化过程中,有两个变量x和y,
如果给定一个x值,
相应地就确定了一个y值,
那么我们称
y是
x的函数.
其中
x是自变量,y是因变量.
新知讲解
我们来研究前面给出的例子
A1={t|0≤t≤0.5}
B1={S|0≤S≤175}
问题2.某公司要求工人每周工作至少1天,至多不超过6天.工资标准是每人每
天350元,而且每周付一次工资,工资y与一周工作天数x的关系可以表示为:
y=350x
A2={1,2,3,4,5,6}
B2={350,700,1050,1400,1750,2100}
y=350x
A1={t|0≤t≤0.5}
B1={S|0≤S≤175}
在S=350t
作用下,A1到B1存在的对应关系
A2={1,2,3,4,5,6}
B2={350,700,1050,1400,1750,2100}
每一个t
唯一一个S
对应
每一个x
对应
唯一一个y
对应
新知讲解
问题3
下图是北京市2016年11月23日的空气质量指数
(Air
Quality
Index,简称AQI)变化图.如
何根据该图确定这一天内任一时刻th的空气质量指数
(AQI)的值I?你认为这里的I是t的函数吗?
A3=
{t|0≤t≤24}
B3={I|0<I<150}
A3=
{t|0≤t≤24}
B3={I|0<I<150}
图像
每一个x
对应
唯一一个y
问题4:国际上常用恩格尔系数反映一个国家人民生活质量的高低,恩格尔系数越低,生活质
量越高。表1-1中恩格尔系数随时间(年)变化的情况表明,“八五”计划以来,我
国城镇居民的生活质量发生了显著变化。
时间(年)
1991
1992
1993
1994
1995
1996
1997
1998
1999
2000
2001
城镇居民家庭恩格尔系数(%)
53.8
52.9
50.1
49.9
49.9
48.6
46.4
44.5
41.9
39.2
37.9
(恩格尔系数=食物支出金额/总支出金额)
A4
={1991,1992,1993,1994,1995,
1996,1997,1998,1999,2000,2001}
B4={53.8,52.9,50.1,49.9,
48.6,
46.4,44.5,41.9,39.2,37.9}
表格
用集合与对应的语言描述恩格尔系数和时间(年)的关系。
新知讲解
每一个元素
唯一一个元素
对应
上述问题的共同特征有:
(1)都包含两个非空数集,用A,B来表示;
(2)都有一个对应关系;
(3)尽管对应关系的表示方法不同,但它们都有如下特性:对于数集A中的任意一
个数x,按照对应关系,在数集B中都有唯一确定的数y和它对应.
新知讲解
设A、B是非空数集,如果按照某种确定的对应关系
f,使对于集合A中的任意一
个数
x,在集合B中都有唯一确定的数
f(x)
和它对应,就称f:
A→B
为从集合A到集合
B的一个函数,记作:
y=f(x)
,
x∈A
x叫作自变量,集合A叫作函数的定义域,集合{f(x)|x∈A}
叫作函数的值域.
注意:(1)A、B为数集且非空;(2)值域{f(x)|x∈A}
是集合B的一个子集,不一定就是
集合B。(3)强调A中的每一个元素,在B中有且唯一元素对应,既不能没有对应,
也不能多一个,而是恰好一个。
函数的三要素:
定义域
对应关系
值域
新知讲解
新知讲解
例2.结合函数的定义,判断下列对应是不是从数集A到数集B的函数.
A
B
f
1
2
2
4
3
6
7
A
B
f
1
2
2
4
3
6
4
A
B
f
1
2
2
4
3
B
A
f
1
2
2
4
3
6
8
(2)
(3)
(4)
(1)
新知讲解
试一试:判断下列从集合A到集合B的对应是否是函数.
A
B
C
D
新知讲解
下列图形哪个可以表示函数的图象?
A
B
C
D
0
x
y
F
0
x
y
C
0
x
y
E
判断下列对应能否表示y是x的函数
分析:(1)中,任意一个x的值,都有唯一一个y值对应,表示y是x的函数。
(2)中,当x=1时,则y=1或y=-1;即一个x
有二个y值对应,所以不表示函数。
合作探究
初中学过函数的定义域和值域
反比例函数
一次函数
二次函数
a
>
0
a
<
0
图像
定义域
值域
合作探究
试一试:求下列函数的定义域
(1)
函数
f(x)=2x-3
的定义域是?
R
(2)
函数
的定义域是?
(3)
函数
的定义域是?
(4)
函数
的定义域是?
新知讲解
区间的概念
区间的几何表示:在数轴表示时,用实心点表示包括在区间内的端点,用空心点表示不包括在区间内的端点.
实数集R可以用区间表示为(-∞,+∞),“∞”读作
“无穷大”,
“-∞”读作
“负无穷大”,“+∞”读作
“正无穷大”.
新知讲解
新知讲解
我们可以把满足x≥a,x>a,x≤b,x<b的实数x的集合,用区间
分别表示为[a,+∞),(a,+∞),(-∞,b],(-∞,b)
合作探究
合作探究
合作探究
合作探究
课堂练习
试一试:
用区间表示下列集合
1.{x|1≤x≤4}
2.{x|-1
4.{x|x
(-1,2]
[1,5)
(-∞,b)
课堂练习
试一试:练习课本P67
1.求下列函数的定义域(用区间表示):
f(2)=32
f(-2)=-32
f(2)+f(-2)=0
f(a)=3a3+2a
f(-a)=-3a3-2a
f(a)+f(-a)=0
答:(1)不是同一个函数。因为定义域不同
答:(2)不是同一函数,因为g(x)中x≠0,所以定义域不同,故不是同一函数.
课堂总结
1.理解函数的定义,从数集到数集的一一对应关系.
2.根据函数的定义,判断是否是函数及相同函数.
3.求函数的定义域,区间的概念及用区间表示集合.
4.了解构成函数的三要素;
板书设计
函数的定义
设A、B是非空数集,如果按照
某种确定的对应关系
f,使对于集
合A中的任意一个数
x,在集合B中
都有唯一确定的数
f(x)
和它对应,
就称f:
A→B
为从集合A到集合
B的一个函数,记作:
y=f(x)
,
x∈A
区间的概念
作业布置
一、举出几个(三个以上)函数的实际例子,并写出其定义域和值域。
二、课本P721、2、3、4
;
P736、9
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
