2021-2022学年鲁教五四新版八年级上册数学《第4章 图形的平移与旋转》单元测试卷(word版含解析)
文档属性
| 名称 | 2021-2022学年鲁教五四新版八年级上册数学《第4章 图形的平移与旋转》单元测试卷(word版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 309.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-28 00:00:00 | ||
图片预览


文档简介
2021-2022学年鲁教五四新版八年级上册数学《第4章
图形的平移与旋转》单元测试卷
一.选择题
1.下列物体的运动不是旋转的是( )
A.旋转的摩天轮
B.正在走动的时针
C.骑自行车的人
D.正在转动的风车叶片
2.下列事件中,属于旋转运动的是( )
A.小明向北走了4米
B.小明在荡秋千
C.电梯从1楼到12楼
D.一物体从高空坠下
3.如图,长方形ABCD的对角线AC=5,AB=3,BC=4,则图中五个小长方形的周长之和为( )
A.7
B.9
C.14
D.18
4.如图,在一块长方形草地上原有一条等宽的笔直小路,现在要把这条小路改为同样宽度的等宽弯曲小路,则下列结论正确的有( )
A.改造后小路的长度不变
B.改造后小路的长度变小
C.改造后草地部分的面积变小
D.改造后草地部分的面积不变
5.如图,将周长为12的△ABC沿BC方向平移2个单位得到△DEF,则四边形ABFD的周长为( )
A.12
B.14
C.16
D.18
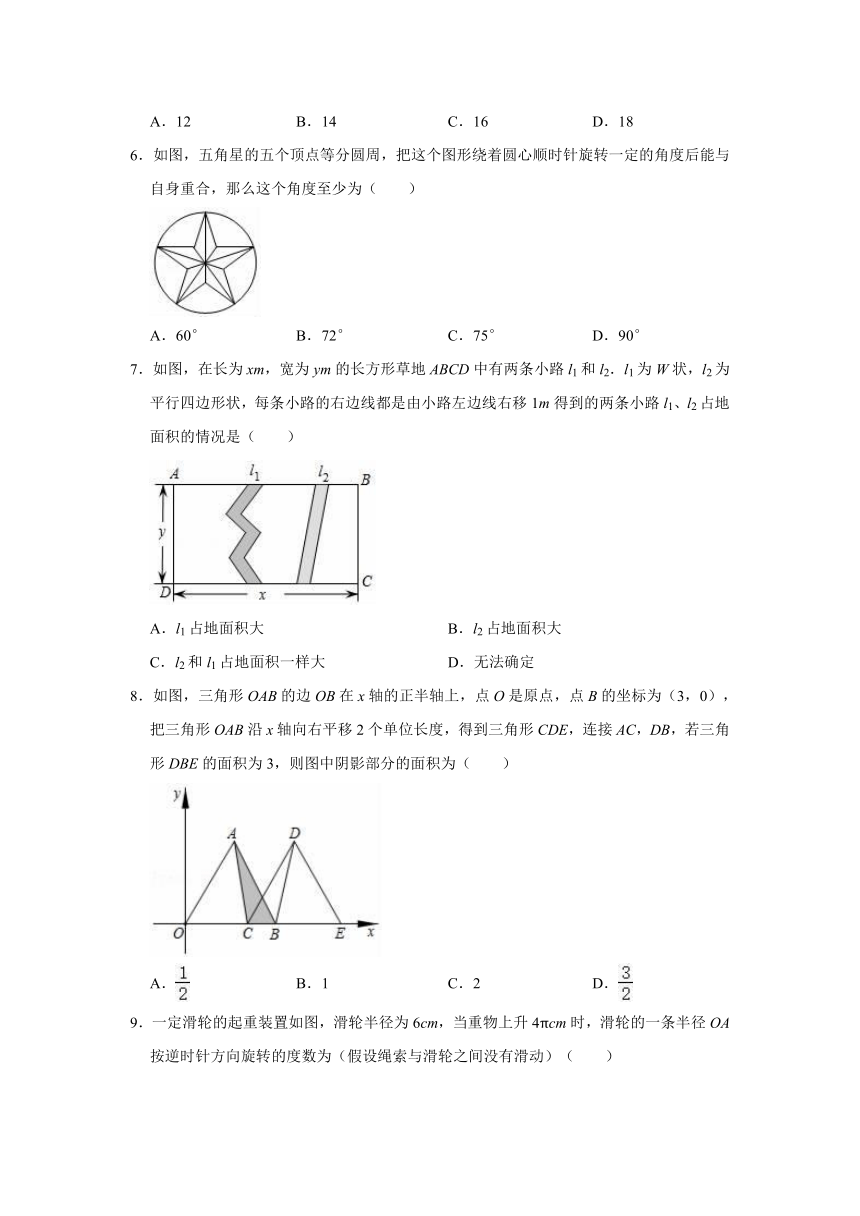
6.如图,五角星的五个顶点等分圆周,把这个图形绕着圆心顺时针旋转一定的角度后能与自身重合,那么这个角度至少为( )
A.60°
B.72°
C.75°
D.90°
7.如图,在长为xm,宽为ym的长方形草地ABCD中有两条小路l1和l2.l1为W状,l2为平行四边形状,每条小路的右边线都是由小路左边线右移1m得到的两条小路l1、l2占地面积的情况是( )
A.l1占地面积大
B.l2占地面积大
C.l2和l1占地面积一样大
D.无法确定
8.如图,三角形OAB的边OB在x轴的正半轴上,点O是原点,点B的坐标为(3,0),把三角形OAB沿x轴向右平移2个单位长度,得到三角形CDE,连接AC,DB,若三角形DBE的面积为3,则图中阴影部分的面积为( )
A.
B.1
C.2
D.
9.一定滑轮的起重装置如图,滑轮半径为6cm,当重物上升4πcm时,滑轮的一条半径OA按逆时针方向旋转的度数为(假设绳索与滑轮之间没有滑动)( )
A.30°
B.60°
C.90°
D.120°
二.填空题
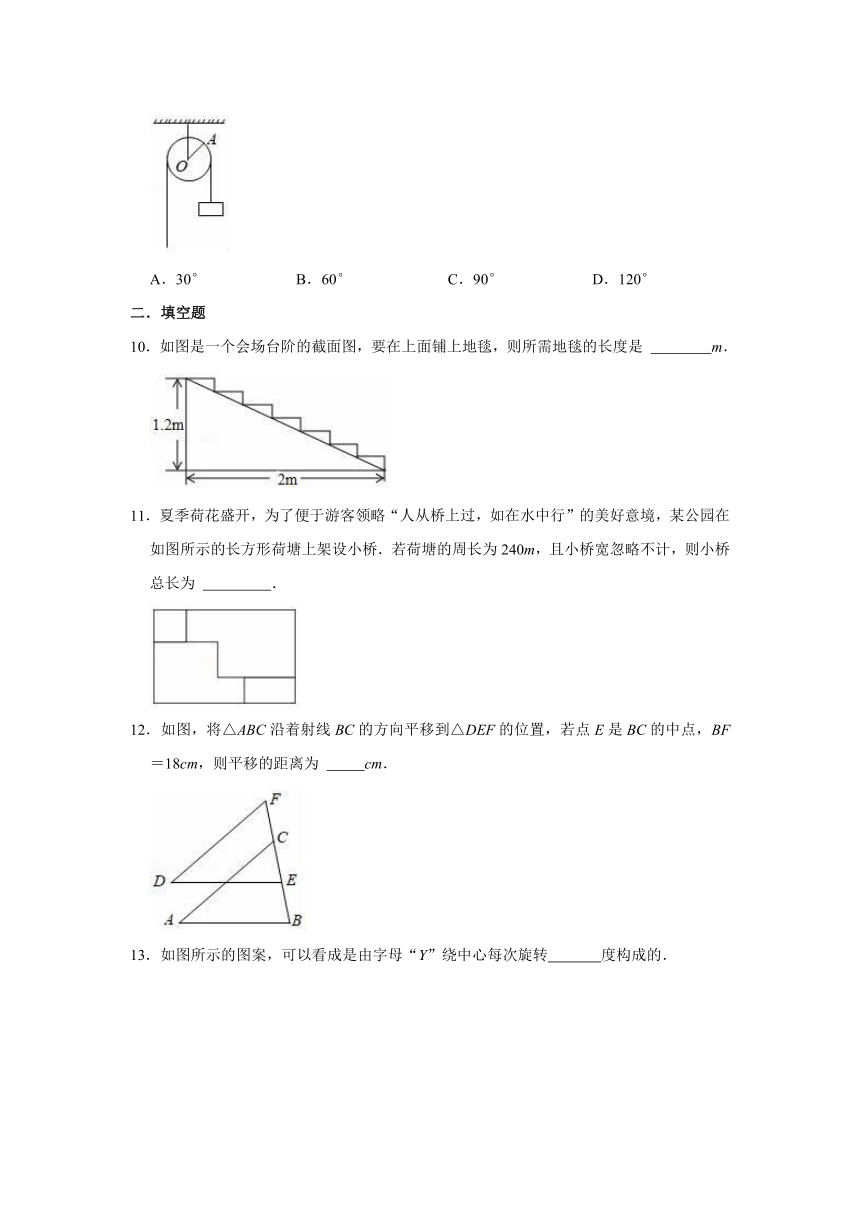
10.如图是一个会场台阶的截面图,要在上面铺上地毯,则所需地毯的长度是
m.
11.夏季荷花盛开,为了便于游客领略“人从桥上过,如在水中行”的美好意境,某公园在如图所示的长方形荷塘上架设小桥.若荷塘的周长为240m,且小桥宽忽略不计,则小桥总长为
.
12.如图,将△ABC沿着射线BC的方向平移到△DEF的位置,若点E是BC的中点,BF=18cm,则平移的距离为
cm.
13.如图所示的图案,可以看成是由字母“Y”绕中心每次旋转
度构成的.
14.夏季荷花盛开,为了便于游客领略“人从桥上过,如在河中行”的美好意境,某景点拟在如图所示的长方形荷塘上架设小桥(图中虚线),若荷塘周长为900m,且桥宽忽略不计,则小桥的总长为
m.
15.把点A(﹣2,﹣3)向右平移3个单位得到的点的坐标为
.
16.镇江市旅游局为了亮化某景点,在两条笔直且互相平行的景观道MN、QP上分别放置A、B两盏激光灯,如图所示.A灯发出的光束自AM逆时针旋转至AN便立即回转;B灯发出的光束自BP逆时针旋转至BQ便立即回转,两灯不间断照射,A灯每秒转动12°,B灯每秒转动4°.B灯先转动12秒,A灯才开始转动.当B灯光束第一次到达BQ之前,两灯的光束互相平行时A灯旋转的时间是
.
17.时钟的时针在不停地旋转,从下午3时到下午6时(同一天),时针旋转的角度是
.
18.一块直角三角板ADC中,D为直角顶点,∠A=30°,将它绕点A顺时针旋转60°,得到△AEB,其中E为直角顶点,则∠BAD=
.
三.解答题
19.如图,一块边长为8米的正方形土地,在上面修了三条道路,宽都是1米,空白的部分种上各种花草.
(1)请利用平移的知识求出种花草的面积.
(2)若空白的部分种植花草共花费了4620元,则每平方米种植花草的费用是多少元?
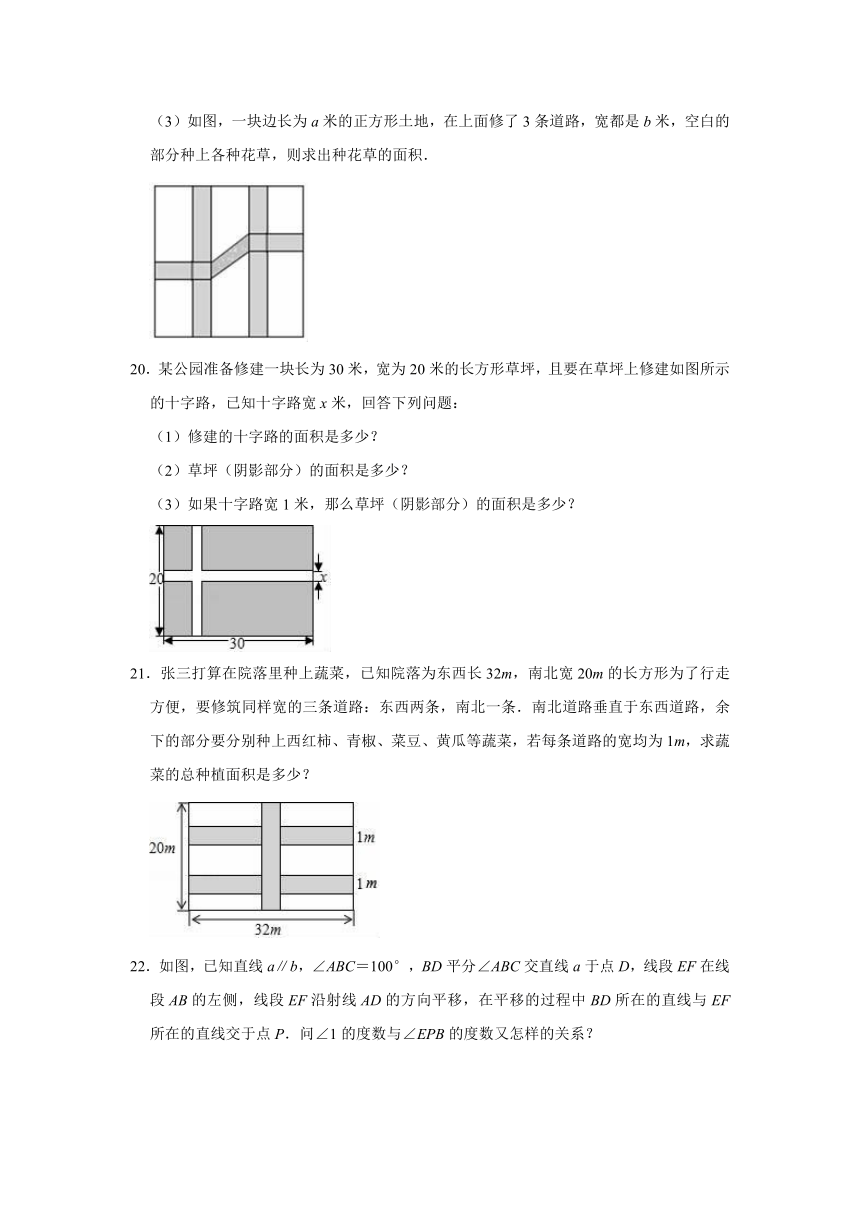
(3)如图,一块边长为a米的正方形土地,在上面修了3条道路,宽都是b米,空白的部分种上各种花草,则求出种花草的面积.
20.某公园准备修建一块长为30米,宽为20米的长方形草坪,且要在草坪上修建如图所示的十字路,已知十字路宽x米,回答下列问题:
(1)修建的十字路的面积是多少?
(2)草坪(阴影部分)的面积是多少?
(3)如果十字路宽1米,那么草坪(阴影部分)的面积是多少?
21.张三打算在院落里种上蔬菜,已知院落为东西长32m,南北宽20m的长方形为了行走方便,要修筑同样宽的三条道路:东西两条,南北一条.南北道路垂直于东西道路,余下的部分要分别种上西红柿、青椒、菜豆、黄瓜等蔬菜,若每条道路的宽均为1m,求蔬菜的总种植面积是多少?
22.如图,已知直线a∥b,∠ABC=100°,BD平分∠ABC交直线a于点D,线段EF在线段AB的左侧,线段EF沿射线AD的方向平移,在平移的过程中BD所在的直线与EF所在的直线交于点P.问∠1的度数与∠EPB的度数又怎样的关系?
【特殊化】
(1)当∠1=40°,交点P在直线a、直线b之间,求∠EPB的度数;
(2)当∠1=70°,求∠EPB的度数;
【一般化】
(3)当∠1=n°,求∠EPB的度数(直接用含n的代数式表示).
23.如图所示的方格纸中,每个小正方形的边长为1,每个小正方形的顶点叫格点,请利用格点画图.
(1)将△ABC向左平移4格,再向上平移1格,请在图中画出平移后的△A'B'C';
(2)△A'B'C'的面积为
;
(3)利用网格在图中画出△A'B'C'的中线B'D,高线B'E;
(4)在图中能使S△PAC=S△BAC的格点P的个数有
个(点P异于B).
24.如图1,A(﹣1,﹣1),B(4,2),C(1,3)
(1)直接写出S△ABC=
;
(2)已知点D(﹣1,m),满足S△BCD=S△ABC,求m的值;
(3)如图2,把直线AC以每秒1个单位长度的速度向右平移,求平移多少秒时该直线恰好经过B点.
25.小明与小刚约好下午4:30在书店门口集合,一同去买课外用书.当小明下午4:00出门赶到书店门口时(路上用去的时间不超过1小时),却没有见到小刚.他怀疑自己迟到了,于是朝书店墙上的时钟一看,只见钟面上的时针与分针刚好重合在一起.请你运用学过的数学知识计算一下,这时的准确时间是多少?
参考答案与试题解析
一.选择题
1.解:骑自行车的人在前进的过程中没有发生旋转.
故选:C.
2.解:小明向北走了4米是平移,A错误;
小明在荡秋千是旋转,B正确;
电梯从1楼到12楼是平移,C错误;
一物体从高空坠下是平移,D错误;
故选:B.
3.解:图中五个小长方形的周长之和=AB+BC+CD+AD=3+4+3+4=14.
故选:C.
4.解:根据平移的性质可知,改造后草地部分的面积不变.
故选:D.
5.解:由平移的性质可知,AC=DF,AD=CF=2,
∵△ABC的周长为12,
∴AB+BC+AC=12,
∴四边形ABFD的周长=AB+BF+FD+AD=AB+BC+CF+DF+AD=12+2+2=16,
故选:C.
6.解:因为五角星的五个顶点等分圆周,
所以360°÷5=72°,
所以这个图形绕着圆心顺时针旋转一定的角度后能与自身重合,
那么这个角度至少为72°.
故选:B.
7.解:小路l1的面积为:xy﹣(x﹣1)y=xy﹣xy+y=y;
小路l2的面积为:xy﹣(x﹣1)y=xy﹣xy+y=y.
所以l2和l1占地面积一样大.
故选:C.
8.解:∵点B的坐标为(3,0),把三角形OAB沿x轴向右平移2个单位长度,
∴BE=2,BC=3﹣2=1,
∵图中阴影部分与三角形DBE等高,三角形DBE的面积为3,
∴图中阴影部分的面积为=3×=.
故选:D.
9.解:设定滑轮逆时针旋转的角度是n°,
由旋转的性质得:重物上升的高度就是点A运动的圆弧长,
∴=4π,
解得:n=120,
故选:D.
二.填空题
10.解:楼梯的长为2m,高为1.2m,则所需地毯的长度是2+1.2=3.2(m).
故答案为:3.2.
11.解:∵荷塘周长为240m,
∴小桥总长为:240÷2=120(m).
故答案为:120m.
12.解:由平移的性质可知:EF=BC,
∵点E是BC的中点,
∴EC=BC=BE,
∴EC=EF=CF,
∵BF=18cm,
∴BE=EC=CF=×18=6(cm),即平移的距离为6cm,
故答案为:6.
13.解:根据图形可得:这是一个由字母“Y”绕着中心连续旋转9次,每次旋转36度角形成的图案.
故答案为:36.
14.解:∵荷塘周长为900m,
∴小桥总长为:900÷2=450(m).
故答案为:450.
15.解:把点A(﹣2,﹣3)向右平移3个单位得到的点的坐标为(﹣2+3,﹣3),
即(1,﹣3),
故答案为:(1,﹣3).
16.解:设A灯旋转时间为t秒,B灯光束第一次到达BQ需要180÷4=45(秒),
∴t≤45﹣12,即t≤33.
由题意,满足以下条件时,两灯的光束能互相平行:
①如图1,∠MAM'=∠PBP',12t=4(12+t),解得t=6;
②如图2,∠NAM'+∠PBP'=180°,12t﹣180+4(12+t)=180,解得t=19.5;
综上所述,满足条件的t的值为6秒或19.5秒.
故答案为:6秒或19.5秒.
17.解:时针从下午3时到下午6时(同一天),3共转了3大格,所以钟表上的时针转过的角度=3×30°=90°.
故答案为:90°.
18.解:根据题意分两种情况画图:
①如图,∵∠DAC=30°,将它绕点A顺时针旋转60°,
∴∠BAC=60°,
∴∠BAD=∠BAC﹣∠DAC=30°;
②如图,∵∠DAC=30°,将它绕点A顺时针旋转60°,
∴∠BAC=60°,
∴∠BAD=∠BAC+∠DAC=90°;
则∠BAD=30°或90°.
故答案为:30°或90°.
三.解答题
19.解:(1)(8﹣2)×(8﹣1)
=6×7=42
(米2);
答:种花草的面积为42米2.
(2)4620÷42=110(元),
答:每平方米种植花草的费用是110元;
(3)(a﹣2b)×(a﹣b)
=a2﹣ab﹣2ab+2b2
=(a2﹣3ab+2b2)(米2).
答:种花草的面积为(a2﹣3ab+2b2)米2.
20.解:(1)30x+20x﹣x2=50x﹣x2.
答:修建十字路的面积是(50x﹣x2)平方米.
(2)30×20﹣(50x﹣x2)=600﹣50x+x2;
答:草坪(阴影部分)的面积是:(600﹣50x+x2)平方米;
(3)600﹣50x+x2
=600﹣50×1+12
=551(平方米).
答:草坪(阴影部分)的面积551平方米.
21.解:结合图形平移的知识,可将题目中的图等效为下图,则图中空白处的面积为所求面积.
结合题中的信息,可得空白处的面积为(32﹣1)×(20﹣2×1)=558(m2),
所以蔬菜的总种植面积为558m2.
22.解:(1)∵BD平分∠ABC,
∴∠ABD=∠DBC=∠ABC=50°,
∵∠EPB是△PFB的外角,
∴∠EPB=∠PFB+∠PBF=∠1+(180°﹣50°)=170°;
(2)①当交点P在直线b的下方时:
∠EPB=∠1﹣50°=20°;
②当交点P在直线a,b之间时:
∠EPB=50°+(180°﹣∠1)=160°;
③当交点P在直线a的上方时:
∠EPB=∠1﹣50°=20°;
(3)①当交点P在直线a,b之间时:∠EPB=180°﹣|n°﹣50°|;
②当交点P在直线a上方或直线b下方时:∠EPB=|n°﹣50°|;
23.解:(1)如图,△A'B'C'为所作;
(2)△A'B'C'的面积=×2×2=4;
故答案为4;
(3)如图,B'D和B'E为所作;
(4)如图,能使S△PAC=S△BAC的格点P的个数有7个.
故答案为7.
24.解:(1)∵A(﹣1,﹣1),B(4,2),C(1,3)
∴S△ABC=20﹣2×4﹣1×3﹣3×5=7;
故答案为:7;
(2)如图,
延长BC交直线x=1于点P,
作CM⊥PD于点M,作BN⊥PD于点N,
∴M(﹣1,3),N(﹣1,2),
设P(﹣1,a),
∴S△CPM+S四边形CMNB=S△PNB,
即2(a﹣3)+(2+5)×1=5(a﹣2),
解得a=,
∴P(﹣1,).
∵SPBD﹣S△PCD=S△BCD,
即5|m﹣|﹣2|m﹣|=7,
解得m=6或m=;
(3)如图,
作BH⊥y轴交AC于点H,
∵S△ABC=S△ABH+S△BCH=7,
∴BH(1+3)=7,
解得BH=,
∴÷1=.
答:平移秒时该直线恰好经过B点.
25.解:分针的速度是时针速度的12倍,设时针走了x°,则分针走了12x°,
∵小明下午4:00出门赶到书店门口时(路上用去的时间不超过1小时),且时针与分针刚好重合在一起.
∴12x°﹣x°=120°,解得x°=°,
∵时针走1°相当于2分钟,
∴时针走过的分钟为°×2=21分.
∴这时准确的时间为4时21分.
图形的平移与旋转》单元测试卷
一.选择题
1.下列物体的运动不是旋转的是( )
A.旋转的摩天轮
B.正在走动的时针
C.骑自行车的人
D.正在转动的风车叶片
2.下列事件中,属于旋转运动的是( )
A.小明向北走了4米
B.小明在荡秋千
C.电梯从1楼到12楼
D.一物体从高空坠下
3.如图,长方形ABCD的对角线AC=5,AB=3,BC=4,则图中五个小长方形的周长之和为( )
A.7
B.9
C.14
D.18
4.如图,在一块长方形草地上原有一条等宽的笔直小路,现在要把这条小路改为同样宽度的等宽弯曲小路,则下列结论正确的有( )
A.改造后小路的长度不变
B.改造后小路的长度变小
C.改造后草地部分的面积变小
D.改造后草地部分的面积不变
5.如图,将周长为12的△ABC沿BC方向平移2个单位得到△DEF,则四边形ABFD的周长为( )
A.12
B.14
C.16
D.18
6.如图,五角星的五个顶点等分圆周,把这个图形绕着圆心顺时针旋转一定的角度后能与自身重合,那么这个角度至少为( )
A.60°
B.72°
C.75°
D.90°
7.如图,在长为xm,宽为ym的长方形草地ABCD中有两条小路l1和l2.l1为W状,l2为平行四边形状,每条小路的右边线都是由小路左边线右移1m得到的两条小路l1、l2占地面积的情况是( )
A.l1占地面积大
B.l2占地面积大
C.l2和l1占地面积一样大
D.无法确定
8.如图,三角形OAB的边OB在x轴的正半轴上,点O是原点,点B的坐标为(3,0),把三角形OAB沿x轴向右平移2个单位长度,得到三角形CDE,连接AC,DB,若三角形DBE的面积为3,则图中阴影部分的面积为( )
A.
B.1
C.2
D.
9.一定滑轮的起重装置如图,滑轮半径为6cm,当重物上升4πcm时,滑轮的一条半径OA按逆时针方向旋转的度数为(假设绳索与滑轮之间没有滑动)( )
A.30°
B.60°
C.90°
D.120°
二.填空题
10.如图是一个会场台阶的截面图,要在上面铺上地毯,则所需地毯的长度是
m.
11.夏季荷花盛开,为了便于游客领略“人从桥上过,如在水中行”的美好意境,某公园在如图所示的长方形荷塘上架设小桥.若荷塘的周长为240m,且小桥宽忽略不计,则小桥总长为
.
12.如图,将△ABC沿着射线BC的方向平移到△DEF的位置,若点E是BC的中点,BF=18cm,则平移的距离为
cm.
13.如图所示的图案,可以看成是由字母“Y”绕中心每次旋转
度构成的.
14.夏季荷花盛开,为了便于游客领略“人从桥上过,如在河中行”的美好意境,某景点拟在如图所示的长方形荷塘上架设小桥(图中虚线),若荷塘周长为900m,且桥宽忽略不计,则小桥的总长为
m.
15.把点A(﹣2,﹣3)向右平移3个单位得到的点的坐标为
.
16.镇江市旅游局为了亮化某景点,在两条笔直且互相平行的景观道MN、QP上分别放置A、B两盏激光灯,如图所示.A灯发出的光束自AM逆时针旋转至AN便立即回转;B灯发出的光束自BP逆时针旋转至BQ便立即回转,两灯不间断照射,A灯每秒转动12°,B灯每秒转动4°.B灯先转动12秒,A灯才开始转动.当B灯光束第一次到达BQ之前,两灯的光束互相平行时A灯旋转的时间是
.
17.时钟的时针在不停地旋转,从下午3时到下午6时(同一天),时针旋转的角度是
.
18.一块直角三角板ADC中,D为直角顶点,∠A=30°,将它绕点A顺时针旋转60°,得到△AEB,其中E为直角顶点,则∠BAD=
.
三.解答题
19.如图,一块边长为8米的正方形土地,在上面修了三条道路,宽都是1米,空白的部分种上各种花草.
(1)请利用平移的知识求出种花草的面积.
(2)若空白的部分种植花草共花费了4620元,则每平方米种植花草的费用是多少元?
(3)如图,一块边长为a米的正方形土地,在上面修了3条道路,宽都是b米,空白的部分种上各种花草,则求出种花草的面积.
20.某公园准备修建一块长为30米,宽为20米的长方形草坪,且要在草坪上修建如图所示的十字路,已知十字路宽x米,回答下列问题:
(1)修建的十字路的面积是多少?
(2)草坪(阴影部分)的面积是多少?
(3)如果十字路宽1米,那么草坪(阴影部分)的面积是多少?
21.张三打算在院落里种上蔬菜,已知院落为东西长32m,南北宽20m的长方形为了行走方便,要修筑同样宽的三条道路:东西两条,南北一条.南北道路垂直于东西道路,余下的部分要分别种上西红柿、青椒、菜豆、黄瓜等蔬菜,若每条道路的宽均为1m,求蔬菜的总种植面积是多少?
22.如图,已知直线a∥b,∠ABC=100°,BD平分∠ABC交直线a于点D,线段EF在线段AB的左侧,线段EF沿射线AD的方向平移,在平移的过程中BD所在的直线与EF所在的直线交于点P.问∠1的度数与∠EPB的度数又怎样的关系?
【特殊化】
(1)当∠1=40°,交点P在直线a、直线b之间,求∠EPB的度数;
(2)当∠1=70°,求∠EPB的度数;
【一般化】
(3)当∠1=n°,求∠EPB的度数(直接用含n的代数式表示).
23.如图所示的方格纸中,每个小正方形的边长为1,每个小正方形的顶点叫格点,请利用格点画图.
(1)将△ABC向左平移4格,再向上平移1格,请在图中画出平移后的△A'B'C';
(2)△A'B'C'的面积为
;
(3)利用网格在图中画出△A'B'C'的中线B'D,高线B'E;
(4)在图中能使S△PAC=S△BAC的格点P的个数有
个(点P异于B).
24.如图1,A(﹣1,﹣1),B(4,2),C(1,3)
(1)直接写出S△ABC=
;
(2)已知点D(﹣1,m),满足S△BCD=S△ABC,求m的值;
(3)如图2,把直线AC以每秒1个单位长度的速度向右平移,求平移多少秒时该直线恰好经过B点.
25.小明与小刚约好下午4:30在书店门口集合,一同去买课外用书.当小明下午4:00出门赶到书店门口时(路上用去的时间不超过1小时),却没有见到小刚.他怀疑自己迟到了,于是朝书店墙上的时钟一看,只见钟面上的时针与分针刚好重合在一起.请你运用学过的数学知识计算一下,这时的准确时间是多少?
参考答案与试题解析
一.选择题
1.解:骑自行车的人在前进的过程中没有发生旋转.
故选:C.
2.解:小明向北走了4米是平移,A错误;
小明在荡秋千是旋转,B正确;
电梯从1楼到12楼是平移,C错误;
一物体从高空坠下是平移,D错误;
故选:B.
3.解:图中五个小长方形的周长之和=AB+BC+CD+AD=3+4+3+4=14.
故选:C.
4.解:根据平移的性质可知,改造后草地部分的面积不变.
故选:D.
5.解:由平移的性质可知,AC=DF,AD=CF=2,
∵△ABC的周长为12,
∴AB+BC+AC=12,
∴四边形ABFD的周长=AB+BF+FD+AD=AB+BC+CF+DF+AD=12+2+2=16,
故选:C.
6.解:因为五角星的五个顶点等分圆周,
所以360°÷5=72°,
所以这个图形绕着圆心顺时针旋转一定的角度后能与自身重合,
那么这个角度至少为72°.
故选:B.
7.解:小路l1的面积为:xy﹣(x﹣1)y=xy﹣xy+y=y;
小路l2的面积为:xy﹣(x﹣1)y=xy﹣xy+y=y.
所以l2和l1占地面积一样大.
故选:C.
8.解:∵点B的坐标为(3,0),把三角形OAB沿x轴向右平移2个单位长度,
∴BE=2,BC=3﹣2=1,
∵图中阴影部分与三角形DBE等高,三角形DBE的面积为3,
∴图中阴影部分的面积为=3×=.
故选:D.
9.解:设定滑轮逆时针旋转的角度是n°,
由旋转的性质得:重物上升的高度就是点A运动的圆弧长,
∴=4π,
解得:n=120,
故选:D.
二.填空题
10.解:楼梯的长为2m,高为1.2m,则所需地毯的长度是2+1.2=3.2(m).
故答案为:3.2.
11.解:∵荷塘周长为240m,
∴小桥总长为:240÷2=120(m).
故答案为:120m.
12.解:由平移的性质可知:EF=BC,
∵点E是BC的中点,
∴EC=BC=BE,
∴EC=EF=CF,
∵BF=18cm,
∴BE=EC=CF=×18=6(cm),即平移的距离为6cm,
故答案为:6.
13.解:根据图形可得:这是一个由字母“Y”绕着中心连续旋转9次,每次旋转36度角形成的图案.
故答案为:36.
14.解:∵荷塘周长为900m,
∴小桥总长为:900÷2=450(m).
故答案为:450.
15.解:把点A(﹣2,﹣3)向右平移3个单位得到的点的坐标为(﹣2+3,﹣3),
即(1,﹣3),
故答案为:(1,﹣3).
16.解:设A灯旋转时间为t秒,B灯光束第一次到达BQ需要180÷4=45(秒),
∴t≤45﹣12,即t≤33.
由题意,满足以下条件时,两灯的光束能互相平行:
①如图1,∠MAM'=∠PBP',12t=4(12+t),解得t=6;
②如图2,∠NAM'+∠PBP'=180°,12t﹣180+4(12+t)=180,解得t=19.5;
综上所述,满足条件的t的值为6秒或19.5秒.
故答案为:6秒或19.5秒.
17.解:时针从下午3时到下午6时(同一天),3共转了3大格,所以钟表上的时针转过的角度=3×30°=90°.
故答案为:90°.
18.解:根据题意分两种情况画图:
①如图,∵∠DAC=30°,将它绕点A顺时针旋转60°,
∴∠BAC=60°,
∴∠BAD=∠BAC﹣∠DAC=30°;
②如图,∵∠DAC=30°,将它绕点A顺时针旋转60°,
∴∠BAC=60°,
∴∠BAD=∠BAC+∠DAC=90°;
则∠BAD=30°或90°.
故答案为:30°或90°.
三.解答题
19.解:(1)(8﹣2)×(8﹣1)
=6×7=42
(米2);
答:种花草的面积为42米2.
(2)4620÷42=110(元),
答:每平方米种植花草的费用是110元;
(3)(a﹣2b)×(a﹣b)
=a2﹣ab﹣2ab+2b2
=(a2﹣3ab+2b2)(米2).
答:种花草的面积为(a2﹣3ab+2b2)米2.
20.解:(1)30x+20x﹣x2=50x﹣x2.
答:修建十字路的面积是(50x﹣x2)平方米.
(2)30×20﹣(50x﹣x2)=600﹣50x+x2;
答:草坪(阴影部分)的面积是:(600﹣50x+x2)平方米;
(3)600﹣50x+x2
=600﹣50×1+12
=551(平方米).
答:草坪(阴影部分)的面积551平方米.
21.解:结合图形平移的知识,可将题目中的图等效为下图,则图中空白处的面积为所求面积.
结合题中的信息,可得空白处的面积为(32﹣1)×(20﹣2×1)=558(m2),
所以蔬菜的总种植面积为558m2.
22.解:(1)∵BD平分∠ABC,
∴∠ABD=∠DBC=∠ABC=50°,
∵∠EPB是△PFB的外角,
∴∠EPB=∠PFB+∠PBF=∠1+(180°﹣50°)=170°;
(2)①当交点P在直线b的下方时:
∠EPB=∠1﹣50°=20°;
②当交点P在直线a,b之间时:
∠EPB=50°+(180°﹣∠1)=160°;
③当交点P在直线a的上方时:
∠EPB=∠1﹣50°=20°;
(3)①当交点P在直线a,b之间时:∠EPB=180°﹣|n°﹣50°|;
②当交点P在直线a上方或直线b下方时:∠EPB=|n°﹣50°|;
23.解:(1)如图,△A'B'C'为所作;
(2)△A'B'C'的面积=×2×2=4;
故答案为4;
(3)如图,B'D和B'E为所作;
(4)如图,能使S△PAC=S△BAC的格点P的个数有7个.
故答案为7.
24.解:(1)∵A(﹣1,﹣1),B(4,2),C(1,3)
∴S△ABC=20﹣2×4﹣1×3﹣3×5=7;
故答案为:7;
(2)如图,
延长BC交直线x=1于点P,
作CM⊥PD于点M,作BN⊥PD于点N,
∴M(﹣1,3),N(﹣1,2),
设P(﹣1,a),
∴S△CPM+S四边形CMNB=S△PNB,
即2(a﹣3)+(2+5)×1=5(a﹣2),
解得a=,
∴P(﹣1,).
∵SPBD﹣S△PCD=S△BCD,
即5|m﹣|﹣2|m﹣|=7,
解得m=6或m=;
(3)如图,
作BH⊥y轴交AC于点H,
∵S△ABC=S△ABH+S△BCH=7,
∴BH(1+3)=7,
解得BH=,
∴÷1=.
答:平移秒时该直线恰好经过B点.
25.解:分针的速度是时针速度的12倍,设时针走了x°,则分针走了12x°,
∵小明下午4:00出门赶到书店门口时(路上用去的时间不超过1小时),且时针与分针刚好重合在一起.
∴12x°﹣x°=120°,解得x°=°,
∵时针走1°相当于2分钟,
∴时针走过的分钟为°×2=21分.
∴这时准确的时间为4时21分.
