2021-2022学年北京课改新版七年级上册数学《第3章 简单的几何图形》单元测试卷(word版含解析)
文档属性
| 名称 | 2021-2022学年北京课改新版七年级上册数学《第3章 简单的几何图形》单元测试卷(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 189.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-28 21:57:56 | ||
图片预览



文档简介
2021-2022学年北京课改新版七年级上册数学《第3章
简单的几何图形》单元测试卷
一.选择题
1.棱长为acm的正方体表面积是( )cm2.
A.4a2
B.6a3
C.a3
D.6a2
2.某班数学老师结合中国共产党建党一百周年,在班级内组织了一堂“正方体展开图猜猜看”活动课,下图是该正方体展开图的一种,那么原正方体中,与“党”字所在面对面上的汉字是( )
A.礼
B.年
C.百
D.赞
3.如图,下列生活物品中,从整体上看,形状是圆柱的是( )
A.
B.
C.
D.
4.圆锥的底面半径扩大到原来的2倍,高不变,它的体积扩大到原来的( )
A.2倍
B.3倍
C.4倍
D.6倍
5.一个圆形表演台,半径3m,现在进行扩建,把半径增加3m,扩建后的圆形表演台的面积是原来面积的( )倍.
A.4
B.6
C.8
D.9
6.在一个不透明的布袋中,装有一个简单几何体模型,甲乙两人在摸后各说出了它的一个特征,甲:它有曲面;乙:它有顶点.该几何体模型可能是( )
A.球
B.三棱锥
C.圆锥
D.圆柱
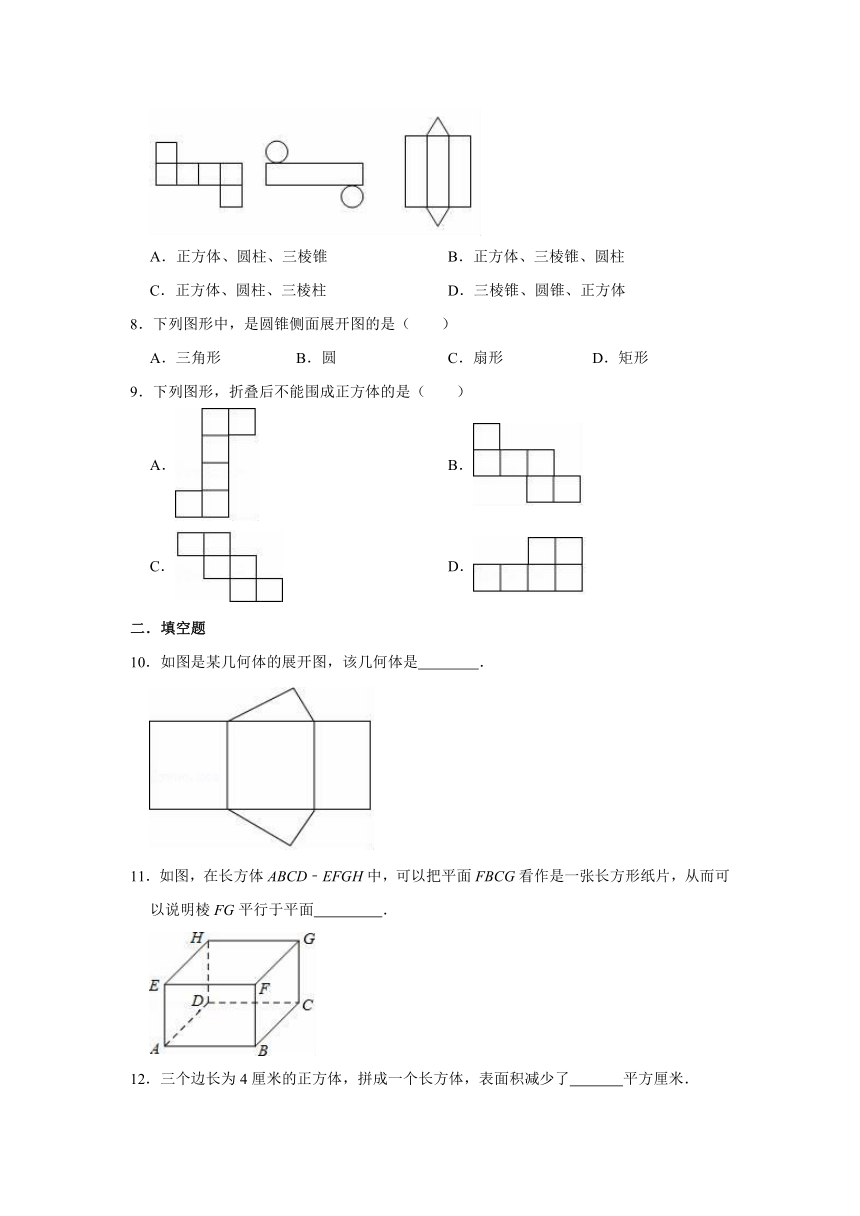
7.如图,以下三个图形是由立体图形展开得到的,相应的立体图形的顺次是( )
A.正方体、圆柱、三棱锥
B.正方体、三棱锥、圆柱
C.正方体、圆柱、三棱柱
D.三棱锥、圆锥、正方体
8.下列图形中,是圆锥侧面展开图的是( )
A.三角形
B.圆
C.扇形
D.矩形
9.下列图形,折叠后不能围成正方体的是( )
A.
B.
C.
D.
二.填空题
10.如图是某几何体的展开图,该几何体是
.
11.如图,在长方体ABCD﹣EFGH中,可以把平面FBCG看作是一张长方形纸片,从而可以说明棱FG平行于平面
.
12.三个边长为4厘米的正方体,拼成一个长方体,表面积减少了
平方厘米.
13.如图是一个长方体的图形,它的每条棱都是一条线段,
请你从这些线段所在的直线中找出:
(1)一对平行的线段:
(写出一对即可);
(2)一对不在同一平面内的线段:
(写出一对即可).
14.如图是某个几何体的展开图,则这个几何体是
.
15.如果一个六棱柱的所有侧棱长之和是48cm,则它的侧棱长为
cm.
16.一个五棱柱的面数为
个,棱数为
条,顶点数为
个.
17.一个圆的周长是62.8m,半径增加了2m后,面积增加了
m2.(π取3.14)
18.如图1,在长为a,宽为b的长方形的四个角,各剪去一个边长为x的小正方形,从而折成如图2的长方体盒子,则用代数式表示图1中阴影部分的面积为
.
19.如图是一个正方体的平面展开图,正方体中相对的面上的数字或代数式互为相反数.则:
(1)x的值为
;
(2)x2﹣y的值为
.
三.解答题
20.下面两个立体图形的名称是:
.
21.甲和乙均是容积为V立方分米无盖的长方体盒子.
(1)如图1,甲盒子底面是边长为a分米的正方形,这个盒子的高是
分米;这个盒子的表面积是
平方分米.(用含有a,V的式子表示)
(2)如图2,乙盒子底面是长方形,甲盒子比乙盒子高5分米.当V=90时,选用2元/平方分米的材料制作甲和乙两个盒子的底面,乙盒子底面制作费用是甲盒子底面制作费用的2倍,求乙盒子的高.(列分式方程求解)
(3)在(2)的条件下,若甲盒子侧面制作材料的费用为0.5元/平方分米,则甲盒子的制作费用是
元.
22.在一个边长为20cm的正方形内画一个最大的圆,这个圆的面积是多少?
23.如图所示的长方形是圆柱的侧面展开图,如果这个长方形相邻的两边长分别为6,4π,求圆柱的体积(温馨提示:考虑问题要全面哦!).
24.推导猜测
(1)三棱锥有
条棱,四棱锥有
条棱,五棱锥有
条棱.
(2)
棱锥有30条棱.
(3)一个棱锥的棱数是100,则这个棱锥是
棱锥,面数是
.
25.[问题提出]
一个边长为ncm
(n≥3)的正方体木块,在它的表面涂上颜色,然后切成边长为1cm的小正方体木块,没有涂上颜色的有多少块?只有一面涂上颜色的有多少块?有两面涂上颜色的有多少块?有三面涂上颜色的多少块?
[问题探究]
我们先从特殊的情况入手
(1)当n=3时,如图(1)
没有涂色的:把这个正方形的表层“剥去”剩下的正方体,有1×1×1=1个小正方体;
一面涂色的:在面上,每个面上有1个,共有6个;
两面涂色的:在棱上,每个棱上有1个,共有12个;
三面涂色的:在顶点处,每个顶点处有1个,共有8个.
(2)当n=4时,如图(2)
没有涂色的:把这个正方形的表层“剥去”剩下的正方体,有2×2×2=8个小正方体:
一面涂色的:在面上,每个面上有4个,6个面,共有24个;
两面涂色的:在棱上,每个楼上有2个,共有24个;
三面涂色的:在顶点处,每个顶点处有1个,共有8个.
…
[问题解决]
一个边长为ncm
(n≥3)的正方体木块,没有涂色的:把这个正方形的表层“剥去”剩下的正方体,有
个小正方体;一面涂色的:在面上,共有
个;
两面涂色的:在棱上,共有
个;
三面涂色的:在顶点处,共
个.
[问题应用]
一个大的正方体,在它的表面涂上颜色,然后把它切成棱长1cm的小正方体,发现有两面涂色的小正方体有96个,请你求出这个大正方体的体积.
[问题拓展]
把一个长16cm、宽10cm、高8cm的长方体表面涂上红漆,然后把它切成棱长2cm的小正方体,没有面涂色有几块,一面涂色有几块,两面涂色有几块,三面涂色有几块?
26.观察下列多面体,并把表补充完整.
名称
三棱柱
四棱柱
五棱柱
六棱柱
图形
顶点数a
6
10
12
棱数b
9
12
面数c
5
6
8
(1)完成表中的数据;
(2)若某个棱柱由28个面构成,则这个棱柱为
棱柱;
(3)根据表中的规律判断,n棱柱共有
个面,共有
个顶点,共有
条棱;
(4)观察表中的结果,你发现棱柱顶点数、棱数、面数之间有什么关系吗?请直接写出来.
参考答案与试题解析
一.选择题
1.解:棱长为acm的正方体的表面积为:6a2cm2.
故选:D.
2.解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“礼”与“赞”是相对面,
“建”与“百”是相对面,
“党”与“年”是相对面;
故选:B.
3.解:A、形状类似圆柱,故选项正确;
B、形状类似圆锥,故选项错误;
C、形状类似长方体,故选项错误;
D、形状类似球,故选项错误.
故选:A.
4.解:2×2=4.
答:它的体积扩大到原来的4倍.
故选:C.
5.解:3m+3m=6m,
圆形表演台原来的面积:πr2=π×32=9π,
圆形表演台扩建后的面积:πr2=π×62=36π,
36π÷9π=4,
扩建后的圆形表演台的面积是原来面积的4倍.
故选:A.
6.解:A、球有曲面,但是没有顶点,故这个选项不符合题意;
B、三棱锥有顶点,但是没有曲面,故这个选项不符合题意;
C、圆锥既有曲面,又有顶点,故这个选项符合题意;
D、圆柱有曲面,但是没有顶点,故这个选项不符合题意;
故选:C.
7.解:观察图形,由立体图形及其表面展开图的特点可知相应的立体图形顺次是正方体、圆柱、三棱柱.
故选:C.
8.解:圆锥的侧面展开图是扇形,
故选:C.
9.解:由展开图可知:A、B、C能围成正方体,不符合题意;
D、是“田”字形,围成几何体时,有两个面重合,故不能围成正方体,符合题意.
故选:D.
二.填空题
10.解:观察图形可知,这个几何体是三棱柱.
故答案为:三棱柱
11.解:如图,在长方体ABCD﹣EFGH中,可以把平面FBCG看作是一张长方形纸片,从而可以说明棱FG平行于平面ABCD.
故答案为:ABCD.
12.解:三个边长为4厘米的正方体,拼成一个长方体,表面积减少了:4×4×4=64(平方厘米).
故答案为:64
13.解:(1)答案不唯一,如:AB∥FG;
(2)答案不唯一,如:AD与BG.
故答案为:AB∥FG;AD与BG.
14.解:观察图形可知,这个几何体是三棱柱.
故答案为:三棱柱.
15.解:48÷6=8(cm).
故答案为:8.
16.解:一个五棱柱的面数为7个,棱数为15条,顶点数为10个.
故答案为:7,15,10.
17.解:π取近似值3.14,
圆是半径为62.8÷3.14÷2=10(m),
圆原来的面积为:
S=πr2=3.14×102=314(m2),
半径增加了2m后的面积为:
S=πr2=3.14×122=452.16(m2),
452.16﹣314=138.16(m2),
所以半径增加了2m后,面积增加了138.16m2.
故答案为:138.16.
18.解:S=(a﹣2x)(b﹣2x)
=4x2﹣2ax﹣2bx+ab
=4x2﹣2x(a+b)+ab,
所以阴影部分的面积为4x2﹣2x(a+b)+ab,
故答案为:4x2﹣2x(a+b)+ab.
19.解:(1)正方体的表面展开图,相对的面之间一定相隔一个正方形.
“﹣3”与“2x﹣3”是相对面,
“y”与“x”是相对面,
“﹣2”与“2”是相对面,
∵相对的面上的数字或代数式互为相反数,
∴2x﹣3+(﹣3)=0,
x+y=0,
解得x=3,
y=﹣3,
(2)∵x=3,y=﹣3,
∴x2﹣y=32﹣(﹣3)=9+3=12.
故答案为:3,12.
三.解答题
20.解:根据立体图形的特点可知,这两个立体图形的名称是:四棱锥、五棱柱,
故答案为:四棱锥、五棱柱.
21.解:(1)∵容积为V立方分米,底面是边长为a分米的正方形,
∴盒子的高为分米;
∴盒子的表面积为:
a2+4(a?)=a2+(平方分米).
故答案为:,a2+;
(2)设乙盒子的高为x分米,则甲盒子高为(x+5)分米.
根据题意,得:
×2=
解得x=5,
经检验x=5是原方程的解,且符合题意.
答:乙盒子的高为5分米.
(3)由(2)得,甲盒子的高为10分米,
∴10a2=90,解得a=3或a=﹣3(舍去),
∴甲盒子的制作费用为:
32×2+×0.5=78元.
故答案为78.
22.解:r=20÷2=10(cm),
S=πr2≈3.14×102=314(cm2).
答:这个圆的面积是314平方厘米.
23.解:①底面周长为6高为4π,
π×()2×4π
=π××4π
=36;
②底面周长为4π高为6,
π×()2×6
=π×4×6
=24π.
答:这个圆柱的体积可以是36或24π.
24.解:(1)三棱锥有6条棱,四棱锥有8条棱,五棱锥有10条棱.
(2)十五棱锥有30条棱.
(3)一个棱锥的棱数是100,则这个棱锥是五十棱锥,面数是51.
故答案为:6,8,10;十五;五十,51.
25.解:[问题解决]
一个边长为ncm
(n≥3)的正方体木块,没有涂色的:把这个正方形的表层“剥去”剩下的正方体,有(n﹣2)3个小正方体;一面涂色的:在面上,共有6(n﹣2)2个;
两面涂色的:在棱上,共有12(n﹣2)个;
三面涂色的:在顶点处,共8个.
故答案为:(n﹣2)3,6(n﹣2)2,12(n﹣2),8;
[问题应用]
设正方体棱长为ncm,
∵有两面涂色的小正方体有96个,
∴12(n﹣2)=96,
∴n=10,
∴这个大正方体的体积为1000cm3.
[问题拓展]
把一个长16cm、宽10cm、高8cm的长方体表面涂上红漆,把它切成棱长2cm的小正方体,
没有面涂色有(16﹣4)(10﹣4)(8﹣4)÷8=36块,
一面涂色有2[(16﹣4)(8﹣4)÷4+(16﹣4)(10﹣4)÷4+(10﹣4)(8﹣4)÷4]=72块,
两面涂色有4[(16﹣4)÷2+(10﹣4)÷2+(8﹣4)÷2]=44块,
三面涂色有8块.
26.解:(1)填表如下:
名称
三棱柱
四棱柱
五棱柱
六棱柱
图形
顶点数a
6
8
10
12
棱数b
9
12
15
18
面数c
5
6
7
8
(2)若某个棱柱由28个面构成,则这个棱柱为26棱柱;
(3)根据表中的规律判断,n棱柱共有
(n+2)个面,共有
2n个顶点,共有
3n条棱;
(4)a,b,c之间的关系:a+c﹣b=2
故答案为:8;15,18;7;26;(n+2),2n,3n.
简单的几何图形》单元测试卷
一.选择题
1.棱长为acm的正方体表面积是( )cm2.
A.4a2
B.6a3
C.a3
D.6a2
2.某班数学老师结合中国共产党建党一百周年,在班级内组织了一堂“正方体展开图猜猜看”活动课,下图是该正方体展开图的一种,那么原正方体中,与“党”字所在面对面上的汉字是( )
A.礼
B.年
C.百
D.赞
3.如图,下列生活物品中,从整体上看,形状是圆柱的是( )
A.
B.
C.
D.
4.圆锥的底面半径扩大到原来的2倍,高不变,它的体积扩大到原来的( )
A.2倍
B.3倍
C.4倍
D.6倍
5.一个圆形表演台,半径3m,现在进行扩建,把半径增加3m,扩建后的圆形表演台的面积是原来面积的( )倍.
A.4
B.6
C.8
D.9
6.在一个不透明的布袋中,装有一个简单几何体模型,甲乙两人在摸后各说出了它的一个特征,甲:它有曲面;乙:它有顶点.该几何体模型可能是( )
A.球
B.三棱锥
C.圆锥
D.圆柱
7.如图,以下三个图形是由立体图形展开得到的,相应的立体图形的顺次是( )
A.正方体、圆柱、三棱锥
B.正方体、三棱锥、圆柱
C.正方体、圆柱、三棱柱
D.三棱锥、圆锥、正方体
8.下列图形中,是圆锥侧面展开图的是( )
A.三角形
B.圆
C.扇形
D.矩形
9.下列图形,折叠后不能围成正方体的是( )
A.
B.
C.
D.
二.填空题
10.如图是某几何体的展开图,该几何体是
.
11.如图,在长方体ABCD﹣EFGH中,可以把平面FBCG看作是一张长方形纸片,从而可以说明棱FG平行于平面
.
12.三个边长为4厘米的正方体,拼成一个长方体,表面积减少了
平方厘米.
13.如图是一个长方体的图形,它的每条棱都是一条线段,
请你从这些线段所在的直线中找出:
(1)一对平行的线段:
(写出一对即可);
(2)一对不在同一平面内的线段:
(写出一对即可).
14.如图是某个几何体的展开图,则这个几何体是
.
15.如果一个六棱柱的所有侧棱长之和是48cm,则它的侧棱长为
cm.
16.一个五棱柱的面数为
个,棱数为
条,顶点数为
个.
17.一个圆的周长是62.8m,半径增加了2m后,面积增加了
m2.(π取3.14)
18.如图1,在长为a,宽为b的长方形的四个角,各剪去一个边长为x的小正方形,从而折成如图2的长方体盒子,则用代数式表示图1中阴影部分的面积为
.
19.如图是一个正方体的平面展开图,正方体中相对的面上的数字或代数式互为相反数.则:
(1)x的值为
;
(2)x2﹣y的值为
.
三.解答题
20.下面两个立体图形的名称是:
.
21.甲和乙均是容积为V立方分米无盖的长方体盒子.
(1)如图1,甲盒子底面是边长为a分米的正方形,这个盒子的高是
分米;这个盒子的表面积是
平方分米.(用含有a,V的式子表示)
(2)如图2,乙盒子底面是长方形,甲盒子比乙盒子高5分米.当V=90时,选用2元/平方分米的材料制作甲和乙两个盒子的底面,乙盒子底面制作费用是甲盒子底面制作费用的2倍,求乙盒子的高.(列分式方程求解)
(3)在(2)的条件下,若甲盒子侧面制作材料的费用为0.5元/平方分米,则甲盒子的制作费用是
元.
22.在一个边长为20cm的正方形内画一个最大的圆,这个圆的面积是多少?
23.如图所示的长方形是圆柱的侧面展开图,如果这个长方形相邻的两边长分别为6,4π,求圆柱的体积(温馨提示:考虑问题要全面哦!).
24.推导猜测
(1)三棱锥有
条棱,四棱锥有
条棱,五棱锥有
条棱.
(2)
棱锥有30条棱.
(3)一个棱锥的棱数是100,则这个棱锥是
棱锥,面数是
.
25.[问题提出]
一个边长为ncm
(n≥3)的正方体木块,在它的表面涂上颜色,然后切成边长为1cm的小正方体木块,没有涂上颜色的有多少块?只有一面涂上颜色的有多少块?有两面涂上颜色的有多少块?有三面涂上颜色的多少块?
[问题探究]
我们先从特殊的情况入手
(1)当n=3时,如图(1)
没有涂色的:把这个正方形的表层“剥去”剩下的正方体,有1×1×1=1个小正方体;
一面涂色的:在面上,每个面上有1个,共有6个;
两面涂色的:在棱上,每个棱上有1个,共有12个;
三面涂色的:在顶点处,每个顶点处有1个,共有8个.
(2)当n=4时,如图(2)
没有涂色的:把这个正方形的表层“剥去”剩下的正方体,有2×2×2=8个小正方体:
一面涂色的:在面上,每个面上有4个,6个面,共有24个;
两面涂色的:在棱上,每个楼上有2个,共有24个;
三面涂色的:在顶点处,每个顶点处有1个,共有8个.
…
[问题解决]
一个边长为ncm
(n≥3)的正方体木块,没有涂色的:把这个正方形的表层“剥去”剩下的正方体,有
个小正方体;一面涂色的:在面上,共有
个;
两面涂色的:在棱上,共有
个;
三面涂色的:在顶点处,共
个.
[问题应用]
一个大的正方体,在它的表面涂上颜色,然后把它切成棱长1cm的小正方体,发现有两面涂色的小正方体有96个,请你求出这个大正方体的体积.
[问题拓展]
把一个长16cm、宽10cm、高8cm的长方体表面涂上红漆,然后把它切成棱长2cm的小正方体,没有面涂色有几块,一面涂色有几块,两面涂色有几块,三面涂色有几块?
26.观察下列多面体,并把表补充完整.
名称
三棱柱
四棱柱
五棱柱
六棱柱
图形
顶点数a
6
10
12
棱数b
9
12
面数c
5
6
8
(1)完成表中的数据;
(2)若某个棱柱由28个面构成,则这个棱柱为
棱柱;
(3)根据表中的规律判断,n棱柱共有
个面,共有
个顶点,共有
条棱;
(4)观察表中的结果,你发现棱柱顶点数、棱数、面数之间有什么关系吗?请直接写出来.
参考答案与试题解析
一.选择题
1.解:棱长为acm的正方体的表面积为:6a2cm2.
故选:D.
2.解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“礼”与“赞”是相对面,
“建”与“百”是相对面,
“党”与“年”是相对面;
故选:B.
3.解:A、形状类似圆柱,故选项正确;
B、形状类似圆锥,故选项错误;
C、形状类似长方体,故选项错误;
D、形状类似球,故选项错误.
故选:A.
4.解:2×2=4.
答:它的体积扩大到原来的4倍.
故选:C.
5.解:3m+3m=6m,
圆形表演台原来的面积:πr2=π×32=9π,
圆形表演台扩建后的面积:πr2=π×62=36π,
36π÷9π=4,
扩建后的圆形表演台的面积是原来面积的4倍.
故选:A.
6.解:A、球有曲面,但是没有顶点,故这个选项不符合题意;
B、三棱锥有顶点,但是没有曲面,故这个选项不符合题意;
C、圆锥既有曲面,又有顶点,故这个选项符合题意;
D、圆柱有曲面,但是没有顶点,故这个选项不符合题意;
故选:C.
7.解:观察图形,由立体图形及其表面展开图的特点可知相应的立体图形顺次是正方体、圆柱、三棱柱.
故选:C.
8.解:圆锥的侧面展开图是扇形,
故选:C.
9.解:由展开图可知:A、B、C能围成正方体,不符合题意;
D、是“田”字形,围成几何体时,有两个面重合,故不能围成正方体,符合题意.
故选:D.
二.填空题
10.解:观察图形可知,这个几何体是三棱柱.
故答案为:三棱柱
11.解:如图,在长方体ABCD﹣EFGH中,可以把平面FBCG看作是一张长方形纸片,从而可以说明棱FG平行于平面ABCD.
故答案为:ABCD.
12.解:三个边长为4厘米的正方体,拼成一个长方体,表面积减少了:4×4×4=64(平方厘米).
故答案为:64
13.解:(1)答案不唯一,如:AB∥FG;
(2)答案不唯一,如:AD与BG.
故答案为:AB∥FG;AD与BG.
14.解:观察图形可知,这个几何体是三棱柱.
故答案为:三棱柱.
15.解:48÷6=8(cm).
故答案为:8.
16.解:一个五棱柱的面数为7个,棱数为15条,顶点数为10个.
故答案为:7,15,10.
17.解:π取近似值3.14,
圆是半径为62.8÷3.14÷2=10(m),
圆原来的面积为:
S=πr2=3.14×102=314(m2),
半径增加了2m后的面积为:
S=πr2=3.14×122=452.16(m2),
452.16﹣314=138.16(m2),
所以半径增加了2m后,面积增加了138.16m2.
故答案为:138.16.
18.解:S=(a﹣2x)(b﹣2x)
=4x2﹣2ax﹣2bx+ab
=4x2﹣2x(a+b)+ab,
所以阴影部分的面积为4x2﹣2x(a+b)+ab,
故答案为:4x2﹣2x(a+b)+ab.
19.解:(1)正方体的表面展开图,相对的面之间一定相隔一个正方形.
“﹣3”与“2x﹣3”是相对面,
“y”与“x”是相对面,
“﹣2”与“2”是相对面,
∵相对的面上的数字或代数式互为相反数,
∴2x﹣3+(﹣3)=0,
x+y=0,
解得x=3,
y=﹣3,
(2)∵x=3,y=﹣3,
∴x2﹣y=32﹣(﹣3)=9+3=12.
故答案为:3,12.
三.解答题
20.解:根据立体图形的特点可知,这两个立体图形的名称是:四棱锥、五棱柱,
故答案为:四棱锥、五棱柱.
21.解:(1)∵容积为V立方分米,底面是边长为a分米的正方形,
∴盒子的高为分米;
∴盒子的表面积为:
a2+4(a?)=a2+(平方分米).
故答案为:,a2+;
(2)设乙盒子的高为x分米,则甲盒子高为(x+5)分米.
根据题意,得:
×2=
解得x=5,
经检验x=5是原方程的解,且符合题意.
答:乙盒子的高为5分米.
(3)由(2)得,甲盒子的高为10分米,
∴10a2=90,解得a=3或a=﹣3(舍去),
∴甲盒子的制作费用为:
32×2+×0.5=78元.
故答案为78.
22.解:r=20÷2=10(cm),
S=πr2≈3.14×102=314(cm2).
答:这个圆的面积是314平方厘米.
23.解:①底面周长为6高为4π,
π×()2×4π
=π××4π
=36;
②底面周长为4π高为6,
π×()2×6
=π×4×6
=24π.
答:这个圆柱的体积可以是36或24π.
24.解:(1)三棱锥有6条棱,四棱锥有8条棱,五棱锥有10条棱.
(2)十五棱锥有30条棱.
(3)一个棱锥的棱数是100,则这个棱锥是五十棱锥,面数是51.
故答案为:6,8,10;十五;五十,51.
25.解:[问题解决]
一个边长为ncm
(n≥3)的正方体木块,没有涂色的:把这个正方形的表层“剥去”剩下的正方体,有(n﹣2)3个小正方体;一面涂色的:在面上,共有6(n﹣2)2个;
两面涂色的:在棱上,共有12(n﹣2)个;
三面涂色的:在顶点处,共8个.
故答案为:(n﹣2)3,6(n﹣2)2,12(n﹣2),8;
[问题应用]
设正方体棱长为ncm,
∵有两面涂色的小正方体有96个,
∴12(n﹣2)=96,
∴n=10,
∴这个大正方体的体积为1000cm3.
[问题拓展]
把一个长16cm、宽10cm、高8cm的长方体表面涂上红漆,把它切成棱长2cm的小正方体,
没有面涂色有(16﹣4)(10﹣4)(8﹣4)÷8=36块,
一面涂色有2[(16﹣4)(8﹣4)÷4+(16﹣4)(10﹣4)÷4+(10﹣4)(8﹣4)÷4]=72块,
两面涂色有4[(16﹣4)÷2+(10﹣4)÷2+(8﹣4)÷2]=44块,
三面涂色有8块.
26.解:(1)填表如下:
名称
三棱柱
四棱柱
五棱柱
六棱柱
图形
顶点数a
6
8
10
12
棱数b
9
12
15
18
面数c
5
6
7
8
(2)若某个棱柱由28个面构成,则这个棱柱为26棱柱;
(3)根据表中的规律判断,n棱柱共有
(n+2)个面,共有
2n个顶点,共有
3n条棱;
(4)a,b,c之间的关系:a+c﹣b=2
故答案为:8;15,18;7;26;(n+2),2n,3n.
同课章节目录
- 第一章 有理数
- 1.1 负数的引入
- 1.2 用数轴上的点表示有理数
- 1.3 相反数和绝对值
- 1.4 有理数的加法
- 1.5 有理数的减法
- 1.6 有理数加减法的混合运算
- 1.7 有理数的乘法
- 1.8 有理数的除法
- 1.9 有理数的乘方
- 1.10 有理数的混合运算
- 1.11 数的近似和科学记数法
- 1.12 用计算器做有理数的混合运算
- 第二章 一元一次方程
- 2.1 字母表示数
- 2.2 同类项与合并同类项
- 2.3 等式与方程
- 2.4 等式的基本性质
- 2.5 一元一次方程
- 2.6 列方程解应用问题
- 第三章 简单的几何图形
- 3.1 平面图形与立体图形
- 3.2 某些立体图形的展开图
- 3.3 从不同方向观察立体图形
- 3.4 点、线、面、体
- 3.5 直线、射线、线段
- 3.6 角及其分类
- 3.7 角的度量与角的换算
- 3.8 角平分线
- 3.9 两条直线的位置关系
- 3.10 相交线与平行线
- 3.11 用计算机绘图
