2021-2022学年沪教新版八年级上册数学《第19章 几何证明》单元测试卷(word版含解析)
文档属性
| 名称 | 2021-2022学年沪教新版八年级上册数学《第19章 几何证明》单元测试卷(word版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 187.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-28 00:00:00 | ||
图片预览

文档简介
2021-2022学年沪教新版八年级上册数学《第19章
几何证明》单元测试卷
一.选择题
1.下列条件不能判定两个直角三角形全等的是( )
A.两条直角边对应相等
B.斜边和一锐角对应相等
C.斜边和一直角边对应相等
D.两个锐角对应相等
2.下列四个命题中,真命题的是( )
A.同角的补角相等
B.相等的角是对顶角
C.三角形的一个外角大于任何一个内角
D.两条直线被第三条直线所截.内错角相等
3.《中共中央国务院关于促进农民增加收入若干政策的意见》中提出“进一步精简乡镇机构和财政供养人员,积极稳妥地调整乡镇建制,有条件的可实行并村”.《中共中央国务院关于积极发展现代农业扎实推进社会主义新农村建设的若干意见》中明确提出“治理农村人居环境,搞好村庄治理规划和试点,节约农村建设用地”.以上两个政策出台后,山东陆陆续续开展了村庄合并某地兴建的幸福小区的三个出口A、B、C的位置如图所示,物业公司计划在不妨碍小区规划的建设下,想在小区内修建一个电动车充电桩,以方便业主,要求到三个出口的距离都相等,则充电桩应该在( )
A.三条边的垂直平分线的交点处
B.三个角的平分线的交点处
C.三角形三条高线的交点处
D.三角形三条中线的交点处
4.下列四个命题:①平行四边形的对角相等;②矩形的对角相等;③矩形的四个角都是直角;④菱形的四条边都相等;其中逆命题是真命题的是( )
A.①②③④
B.①③④
C.①③
D.①
5.下列命题是真命题的有( )个
①真命题都是定理;②垂直于同一条直线的两条直线平行;③三角形的三条高线交于一点;④有两边和一个角对应相等的两个三角形全等;⑤全等三角形对应边上的高相等;⑥三角形中至少有一个角不小于60°.
A.2
B.3
C.4
D.5
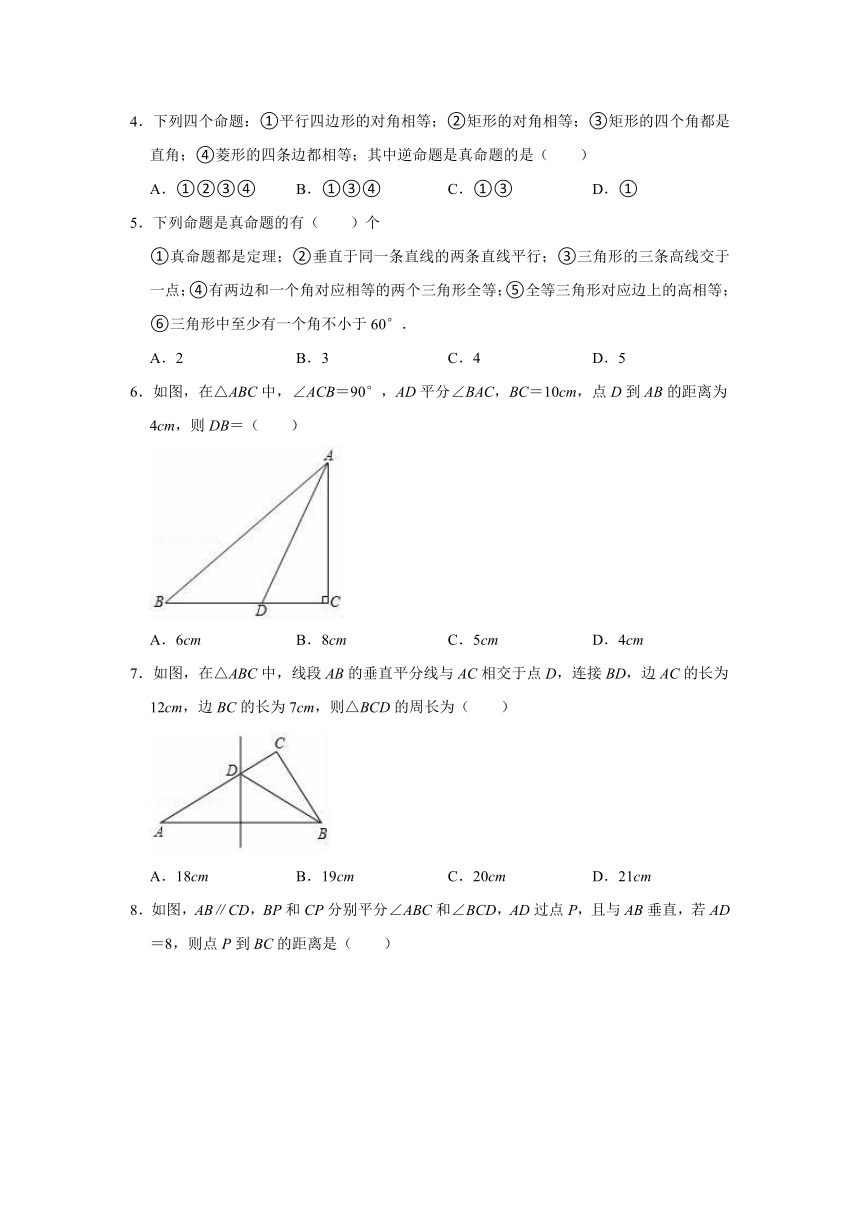
6.如图,在△ABC中,∠ACB=90°,AD平分∠BAC,BC=10cm,点D到AB的距离为4cm,则DB=( )
A.6cm
B.8cm
C.5cm
D.4cm
7.如图,在△ABC中,线段AB的垂直平分线与AC相交于点D,连接BD,边AC的长为12cm,边BC的长为7cm,则△BCD的周长为( )
A.18cm
B.19cm
C.20cm
D.21cm
8.如图,AB∥CD,BP和CP分别平分∠ABC和∠BCD,AD过点P,且与AB垂直,若AD=8,则点P到BC的距离是( )
A.3
B.4
C.5
D.6
二.填空题
9.在平面直角坐标系中,A(x,y)到原点的距离为
.
10.命题“同旁内角互补,两直线平行”的结论是
.
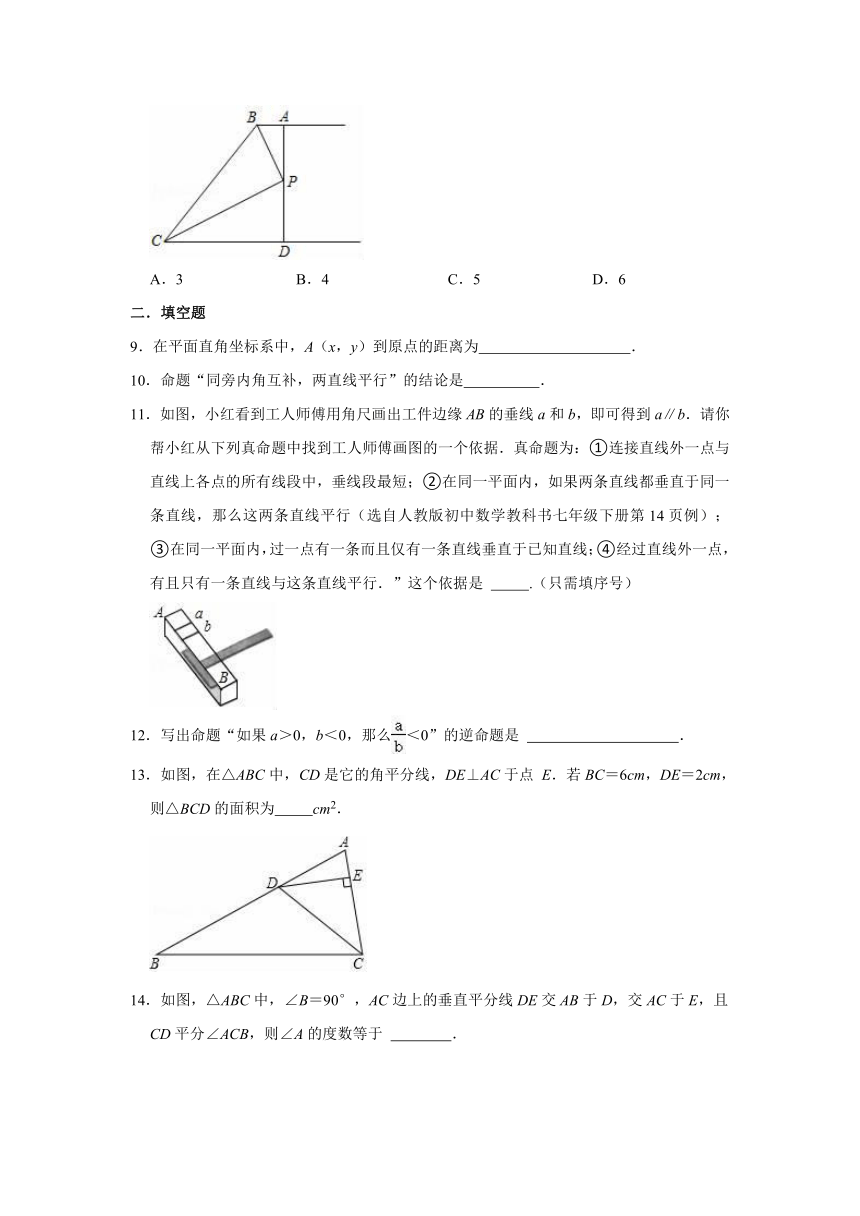
11.如图,小红看到工人师傅用角尺画出工件边缘AB的垂线a和b,即可得到a∥b.请你帮小红从下列真命题中找到工人师傅画图的一个依据.真命题为:①连接直线外一点与直线上各点的所有线段中,垂线段最短;②在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行(选自人教版初中数学教科书七年级下册第14页例);③在同一平面内,过一点有一条而且仅有一条直线垂直于已知直线;④经过直线外一点,有且只有一条直线与这条直线平行.”这个依据是
.(只需填序号)
12.写出命题“如果a>0,b<0,那么<0”的逆命题是
.
13.如图,在△ABC中,CD是它的角平分线,DE⊥AC于点
E.若BC=6cm,DE=2cm,则△BCD的面积为
cm2.
14.如图,△ABC中,∠B=90°,AC边上的垂直平分线DE交AB于D,交AC于E,且CD平分∠ACB,则∠A的度数等于
.
15.如图,△ABC中,DE、FG分别为AB、AC的垂直平分线,DE、FG相交于M点,连接FA、EA,若∠BAC=80°,求∠EAF=
.
16.如图,已知△ABC的周长是18,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=1,△ABC的面积是
.
三.解答题
17.下列各命题都成立,写出它们的逆命题,这些逆命题成立吗?
(1)同旁内角互补,两直线平行.
(2)如果两个角是直角,那么这两个角相等.
18.图形的世界丰富且充满变化,用数学的眼光观察它们,奇妙无比.
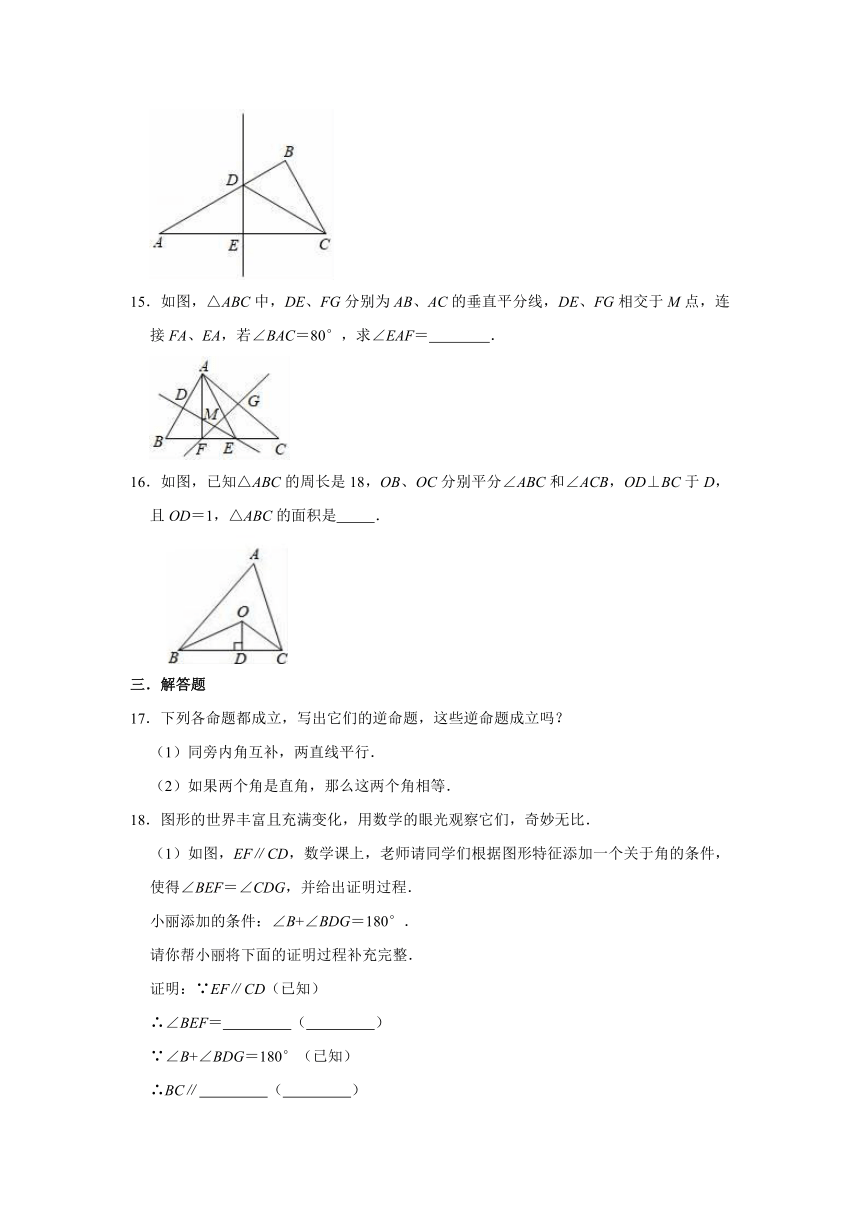
(1)如图,EF∥CD,数学课上,老师请同学们根据图形特征添加一个关于角的条件,使得∠BEF=∠CDG,并给出证明过程.
小丽添加的条件:∠B+∠BDG=180°.
请你帮小丽将下面的证明过程补充完整.
证明:∵EF∥CD(已知)
∴∠BEF=
(
)
∵∠B+∠BDG=180°(已知)
∴BC∥
(
)
∴∠CDG=
(
)
∴∠BEF=∠CDG(等量代换)
(2)拓展:如图,请你从三个选项①DG∥BC,②DG平分∠ADC,③∠B=∠BCD中任选出两个作为条件,另一个作为结论,组成一个真命题,并加以证明.
①条件:
,结论:
(填序号).
②证明:
.
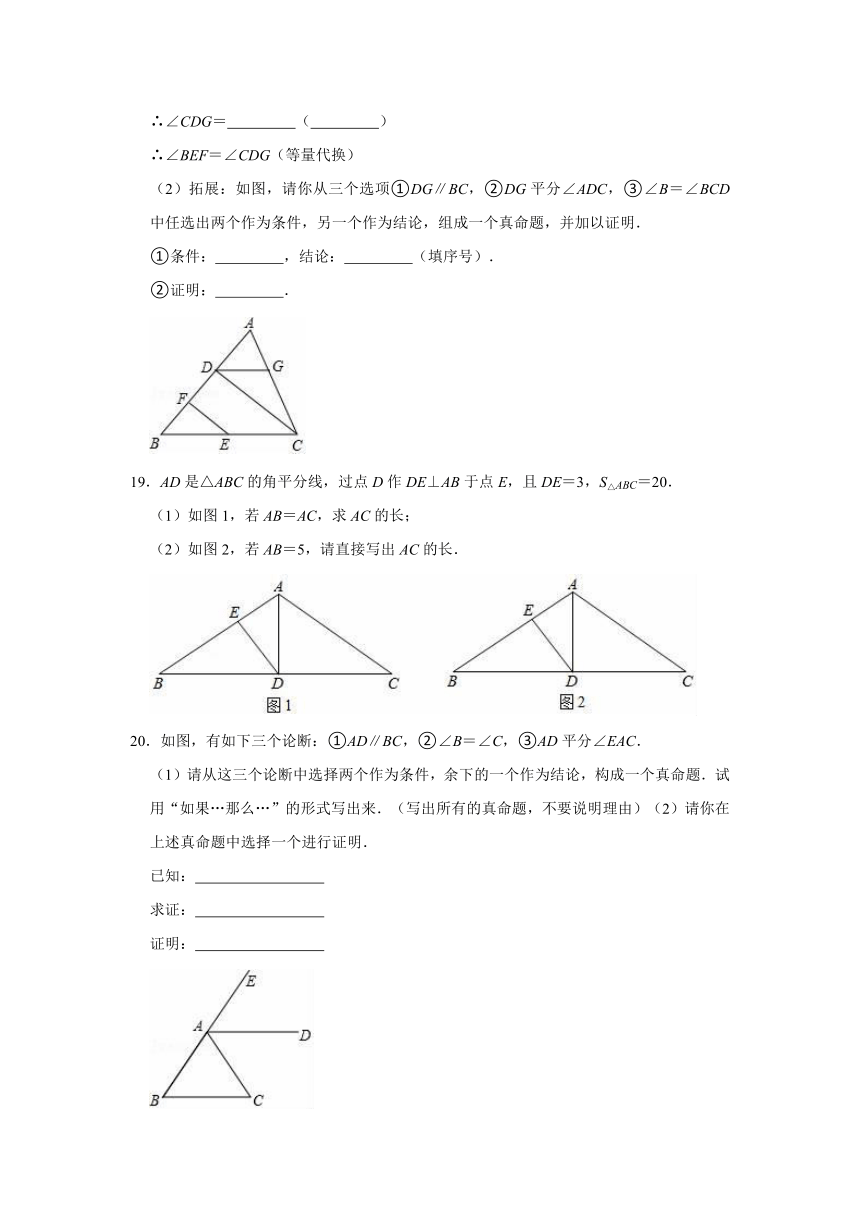
19.AD是△ABC的角平分线,过点D作DE⊥AB于点E,且DE=3,S△ABC=20.
(1)如图1,若AB=AC,求AC的长;
(2)如图2,若AB=5,请直接写出AC的长.
20.如图,有如下三个论断:①AD∥BC,②∠B=∠C,③AD平分∠EAC.
(1)请从这三个论断中选择两个作为条件,余下的一个作为结论,构成一个真命题.试用“如果…那么…”的形式写出来.(写出所有的真命题,不要说明理由)(2)请你在上述真命题中选择一个进行证明.
已知:
求证:
证明:
21.先阅读下列一段文字,再解答问题
已知在平面内有两点P1(x1,y1),P2(x2,y2),其两点间的距离公式为P1P2=,同时,当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|
(1)已知点A(2,4),B(﹣3,﹣8),试求A,B两点间的距离;
(2)已知点A,B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为﹣1,试求A,B两点间的距离;
(3)已知点A(0,6)B(﹣3,2),C(3,2),判断线段AB,BC,AC中哪两条是相等的?并说明理由.
参考答案与试题解析
一.选择题
1.解:A、根据SAS定理可知,两条直角边对应相等的两个三角形全等,本选项不符合题意;
B、根据AAS定理可知,斜边和一锐角对应相等的两个三角形全等,本选项不符合题意;
C、根据HL定理可知,斜边和一直角边对应相等的两个三角形全等,本选项不符合题意;
D、两个锐角对应相等的两个三角形不一定全等,本选项符合题意;
故选:D.
2.解:同角的补角相等,A是真命题;
相等的角不一定是对顶角,B是假命题;
三角形的一个外角大于任何一个与它不相邻的内角,C是假命题;
两条平行线被第三条直线所截.内错角相等,D是假命题;
故选:A.
3.解:∵电动车充电桩到三个出口的距离都相等,
∴充电桩应该在三条边的垂直平分线的交点处,
故选:A.
4.解:①平行四边形的对角相等的逆命题是对角相等的四边形是平行四边形,是真命题;
②矩形的对角相等的逆命题是对角相等的四边形是矩形,是假命题;
③矩形的四个角都是直角的逆命题是四个角都是直角是矩形,是真命题;
④菱形的四条边都相等的逆命题是四条边都相等的四边形是菱形,是真命题;
故选:B.
5.解:①定理的真命题,但真命题不一定都是定理,本说法是假命题;
②在同一平面内,垂直于同一条直线的两条直线平行,本说法是假命题;
③三角形的三条高线所在的直线交于一点,本说法是假命题;
④有两边和两边夹角对应相等的两个三角形全等,本说法是假命题;
⑤全等三角形对应边上的高相等,本说法是真命题;
⑥三角形中至少有一个角不小于60°,本说法是真命题;
故选:A.
6.解:过点D作DE⊥AB于E,
由题意得,DE=4cm,
∵AD平分∠BAC,∠ACB=90°,DE⊥AB,
∴DC=DE=4(cm),
∴BD=BC﹣DC=6(cm),
故选:A.
7.解:∵线段AB的垂直平分线与AC相交于点D,
∴DA=DB,
∴△BCD的周长=BC+CD+DB=BC+CD+DA=BC+AC,
∵AC=12cm,BC=7cm,
∴△BCD的周长=BC+AC=12+7=19(cm),
故选:B.
8.解:过点P作PE⊥BC于E,
∵AB∥CD,AD⊥AB,
∴AD⊥CD,
∵BP平分∠ABC,PA⊥AB,PE⊥BC,
∴PE=AP,
同理可得:PE=PD,
∴PE=AD,
∵AD=8,
∴PE=4,即点P到BC的距离是4,
故选:B.
二.填空题
9.解:平面直角坐标系中任意一点A(x,y)到原点的距离OA=,
故答案为:.
10.解:命题“同旁内角互补,两直线平行”的结论是两直线平行,
故答案为:两直线平行.
11.解:∵a⊥AB,b⊥AB,
∴a∥b,
∴工人师傅画图的一个依据是在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行,
故答案为:②.
12.解:命题“如果a>0,b<0,那么<0”的逆命题是“如果<0,那么a>0,b<0”,
故答案为:如果<0,那么a>0,b<0.
13.解:作DF⊥BC于F,
∵CD是它的角平分线,DE⊥AC,DF⊥BC,
∴DF=DE=2,
∴△BCD的面积=×BC×DF=6(cm2),
故答案为:6.
14.解:∵DE是AC边上的垂直平分线,
∴DA=DC,
∴∠A=∠DCA,
∵CD平分∠ACB,
∴∠BCD=∠DCA,
∴∠A=∠DCA=∠BCD,
∵∠B=90°,
∴∠A=30°,
故答案为:30°.
15.解:∵∠BAC=80°,
∴∠B+∠C=180°﹣80°=100°,
∵DE、FG分别为AB、AC的垂直平分线,
∴EA=EB,FA=FC,
∴∠EAB=∠B,∠FAC=∠C,
∴∠EAB+∠FAC=∠B+∠C=100°,
∴∠EAF=∠EAB+∠FAC﹣∠BAC=100°﹣80°=20°,
故答案为:20°.
16.解:过点O作OE⊥AB于E,OF⊥AC与F,连接OA,
∵OB平分∠ABC,OD⊥BC,OE⊥AB,
∴OE=OD=1,
同理可知,OF=OD=1,
∴△ABC的面积=△OAB的面积+△OAC的面积+△OBC的面积
=×AB×OE+×AC×OF+×BC×OD
=×18×1
=9,
故答案为:9.
三.解答题
17.解:(1)同旁内角互补,两直线平行的逆命题是两直线平行,同旁内角互补,成立;
(2)如果两个角是直角,那么这两个角相等的逆命题是如果两个角相等、那么这两个角是直角,不成立.
18.(1)证明:∵EF∥CD(已知),
∴∠BEF=∠BCD(两直线平行,同位角相等),
∵∠B+∠BDG=180°(已知),
∴BC∥DG(同旁内角互补,两直线平行),
∴∠CDG=∠BCD(两直线平行,内错角相等),
∴∠BEF=∠CDG(等量代换);
(2)①条件:DG∥BC,∠B=∠BCD(答案不唯一),
结论:DG平分∠ADC,
②证明:∵DG∥BC,
∴∠ADG=∠B,∠CDG=∠BCD,
∵∠B=∠BCD,
∴∠ADG=∠CDG,即DG平分∠ADC.
故答案为:(1)∠BCD;两直线平行,同位角相等;DG;同旁内角互补,两直线平行;∠BCD;两直线平行,内错角相等;
(2)①、①③;②,
∵DG∥BC,
∴∠ADG=∠B,∠CDG=∠BCD,
∵∠B=∠BCD,
∴∠ADG=∠CDG,即DG平分∠ADC.
19.解:(1)如图1,作DF⊥AC于F,
∵AD是△ABC的角平分线,DE⊥AB,DF⊥AC,
∴DF=DE=3,
由题意得,×AB×3+×AC×3=20,
解得,AC=AB=;
(2)如图2,作DF⊥AC于F,
∵AD是△ABC的角平分线,DE⊥AB,DF⊥AC,
∴DF=DE=3,
由题意得,×5×3+×AC×3=20,
解得,AC=.
20.(1)解:如果①②,那么③;
如果①③,那么②;
如果②③,那么①;
(2)①已知:AD∥BC,∠B=∠C,求证:AD平分∠EAC;
证明:∵AD∥BC,
∴∠DAE=∠B,∠DAC=∠C,
∵∠B=∠C,
∴∠DAE=∠DAC,
∴AD平分∠EAC;
②已知:AD∥BC,AD平分∠EAC,
求证:∠B=∠C;
证明:∵AD∥BC,
∴∠DAE=∠B,∠DAC=∠C,
∵AD平分∠EAC,
∴∠DAE=∠DAC,
∴∠B=∠C;
③已知:∠B=∠C,AD平分∠EAC,
求证:AD∥BC;
证明:∵∠EAC=∠B+∠C,∠B=∠C,
∴∠EAC=2∠B,
∵AD平分∠EAC,
∴∠EAC=2∠EAD,
∴∠EAD=∠B,
∴AD∥BC.
故答案为:AD∥BC,∠B=∠C;
AD平分∠EAC;
∵AD∥BC,
∴∠DAE=∠B,∠DAC=∠C,
∵∠B=∠C,
∴∠DAE=∠DAC,
∴AD平分∠EAC.
21.解:(1)依据两点间的距离公式,可得AB==13;
(2)当点A,B在平行于y轴的直线上时,AB=|﹣1﹣5|=6;
(3)AB与AC相等.理由:
∵AB==5;
AC==5;
BC=|3﹣(﹣3)|=6.
∴AB=AC.
几何证明》单元测试卷
一.选择题
1.下列条件不能判定两个直角三角形全等的是( )
A.两条直角边对应相等
B.斜边和一锐角对应相等
C.斜边和一直角边对应相等
D.两个锐角对应相等
2.下列四个命题中,真命题的是( )
A.同角的补角相等
B.相等的角是对顶角
C.三角形的一个外角大于任何一个内角
D.两条直线被第三条直线所截.内错角相等
3.《中共中央国务院关于促进农民增加收入若干政策的意见》中提出“进一步精简乡镇机构和财政供养人员,积极稳妥地调整乡镇建制,有条件的可实行并村”.《中共中央国务院关于积极发展现代农业扎实推进社会主义新农村建设的若干意见》中明确提出“治理农村人居环境,搞好村庄治理规划和试点,节约农村建设用地”.以上两个政策出台后,山东陆陆续续开展了村庄合并某地兴建的幸福小区的三个出口A、B、C的位置如图所示,物业公司计划在不妨碍小区规划的建设下,想在小区内修建一个电动车充电桩,以方便业主,要求到三个出口的距离都相等,则充电桩应该在( )
A.三条边的垂直平分线的交点处
B.三个角的平分线的交点处
C.三角形三条高线的交点处
D.三角形三条中线的交点处
4.下列四个命题:①平行四边形的对角相等;②矩形的对角相等;③矩形的四个角都是直角;④菱形的四条边都相等;其中逆命题是真命题的是( )
A.①②③④
B.①③④
C.①③
D.①
5.下列命题是真命题的有( )个
①真命题都是定理;②垂直于同一条直线的两条直线平行;③三角形的三条高线交于一点;④有两边和一个角对应相等的两个三角形全等;⑤全等三角形对应边上的高相等;⑥三角形中至少有一个角不小于60°.
A.2
B.3
C.4
D.5
6.如图,在△ABC中,∠ACB=90°,AD平分∠BAC,BC=10cm,点D到AB的距离为4cm,则DB=( )
A.6cm
B.8cm
C.5cm
D.4cm
7.如图,在△ABC中,线段AB的垂直平分线与AC相交于点D,连接BD,边AC的长为12cm,边BC的长为7cm,则△BCD的周长为( )
A.18cm
B.19cm
C.20cm
D.21cm
8.如图,AB∥CD,BP和CP分别平分∠ABC和∠BCD,AD过点P,且与AB垂直,若AD=8,则点P到BC的距离是( )
A.3
B.4
C.5
D.6
二.填空题
9.在平面直角坐标系中,A(x,y)到原点的距离为
.
10.命题“同旁内角互补,两直线平行”的结论是
.
11.如图,小红看到工人师傅用角尺画出工件边缘AB的垂线a和b,即可得到a∥b.请你帮小红从下列真命题中找到工人师傅画图的一个依据.真命题为:①连接直线外一点与直线上各点的所有线段中,垂线段最短;②在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行(选自人教版初中数学教科书七年级下册第14页例);③在同一平面内,过一点有一条而且仅有一条直线垂直于已知直线;④经过直线外一点,有且只有一条直线与这条直线平行.”这个依据是
.(只需填序号)
12.写出命题“如果a>0,b<0,那么<0”的逆命题是
.
13.如图,在△ABC中,CD是它的角平分线,DE⊥AC于点
E.若BC=6cm,DE=2cm,则△BCD的面积为
cm2.
14.如图,△ABC中,∠B=90°,AC边上的垂直平分线DE交AB于D,交AC于E,且CD平分∠ACB,则∠A的度数等于
.
15.如图,△ABC中,DE、FG分别为AB、AC的垂直平分线,DE、FG相交于M点,连接FA、EA,若∠BAC=80°,求∠EAF=
.
16.如图,已知△ABC的周长是18,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=1,△ABC的面积是
.
三.解答题
17.下列各命题都成立,写出它们的逆命题,这些逆命题成立吗?
(1)同旁内角互补,两直线平行.
(2)如果两个角是直角,那么这两个角相等.
18.图形的世界丰富且充满变化,用数学的眼光观察它们,奇妙无比.
(1)如图,EF∥CD,数学课上,老师请同学们根据图形特征添加一个关于角的条件,使得∠BEF=∠CDG,并给出证明过程.
小丽添加的条件:∠B+∠BDG=180°.
请你帮小丽将下面的证明过程补充完整.
证明:∵EF∥CD(已知)
∴∠BEF=
(
)
∵∠B+∠BDG=180°(已知)
∴BC∥
(
)
∴∠CDG=
(
)
∴∠BEF=∠CDG(等量代换)
(2)拓展:如图,请你从三个选项①DG∥BC,②DG平分∠ADC,③∠B=∠BCD中任选出两个作为条件,另一个作为结论,组成一个真命题,并加以证明.
①条件:
,结论:
(填序号).
②证明:
.
19.AD是△ABC的角平分线,过点D作DE⊥AB于点E,且DE=3,S△ABC=20.
(1)如图1,若AB=AC,求AC的长;
(2)如图2,若AB=5,请直接写出AC的长.
20.如图,有如下三个论断:①AD∥BC,②∠B=∠C,③AD平分∠EAC.
(1)请从这三个论断中选择两个作为条件,余下的一个作为结论,构成一个真命题.试用“如果…那么…”的形式写出来.(写出所有的真命题,不要说明理由)(2)请你在上述真命题中选择一个进行证明.
已知:
求证:
证明:
21.先阅读下列一段文字,再解答问题
已知在平面内有两点P1(x1,y1),P2(x2,y2),其两点间的距离公式为P1P2=,同时,当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|
(1)已知点A(2,4),B(﹣3,﹣8),试求A,B两点间的距离;
(2)已知点A,B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为﹣1,试求A,B两点间的距离;
(3)已知点A(0,6)B(﹣3,2),C(3,2),判断线段AB,BC,AC中哪两条是相等的?并说明理由.
参考答案与试题解析
一.选择题
1.解:A、根据SAS定理可知,两条直角边对应相等的两个三角形全等,本选项不符合题意;
B、根据AAS定理可知,斜边和一锐角对应相等的两个三角形全等,本选项不符合题意;
C、根据HL定理可知,斜边和一直角边对应相等的两个三角形全等,本选项不符合题意;
D、两个锐角对应相等的两个三角形不一定全等,本选项符合题意;
故选:D.
2.解:同角的补角相等,A是真命题;
相等的角不一定是对顶角,B是假命题;
三角形的一个外角大于任何一个与它不相邻的内角,C是假命题;
两条平行线被第三条直线所截.内错角相等,D是假命题;
故选:A.
3.解:∵电动车充电桩到三个出口的距离都相等,
∴充电桩应该在三条边的垂直平分线的交点处,
故选:A.
4.解:①平行四边形的对角相等的逆命题是对角相等的四边形是平行四边形,是真命题;
②矩形的对角相等的逆命题是对角相等的四边形是矩形,是假命题;
③矩形的四个角都是直角的逆命题是四个角都是直角是矩形,是真命题;
④菱形的四条边都相等的逆命题是四条边都相等的四边形是菱形,是真命题;
故选:B.
5.解:①定理的真命题,但真命题不一定都是定理,本说法是假命题;
②在同一平面内,垂直于同一条直线的两条直线平行,本说法是假命题;
③三角形的三条高线所在的直线交于一点,本说法是假命题;
④有两边和两边夹角对应相等的两个三角形全等,本说法是假命题;
⑤全等三角形对应边上的高相等,本说法是真命题;
⑥三角形中至少有一个角不小于60°,本说法是真命题;
故选:A.
6.解:过点D作DE⊥AB于E,
由题意得,DE=4cm,
∵AD平分∠BAC,∠ACB=90°,DE⊥AB,
∴DC=DE=4(cm),
∴BD=BC﹣DC=6(cm),
故选:A.
7.解:∵线段AB的垂直平分线与AC相交于点D,
∴DA=DB,
∴△BCD的周长=BC+CD+DB=BC+CD+DA=BC+AC,
∵AC=12cm,BC=7cm,
∴△BCD的周长=BC+AC=12+7=19(cm),
故选:B.
8.解:过点P作PE⊥BC于E,
∵AB∥CD,AD⊥AB,
∴AD⊥CD,
∵BP平分∠ABC,PA⊥AB,PE⊥BC,
∴PE=AP,
同理可得:PE=PD,
∴PE=AD,
∵AD=8,
∴PE=4,即点P到BC的距离是4,
故选:B.
二.填空题
9.解:平面直角坐标系中任意一点A(x,y)到原点的距离OA=,
故答案为:.
10.解:命题“同旁内角互补,两直线平行”的结论是两直线平行,
故答案为:两直线平行.
11.解:∵a⊥AB,b⊥AB,
∴a∥b,
∴工人师傅画图的一个依据是在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行,
故答案为:②.
12.解:命题“如果a>0,b<0,那么<0”的逆命题是“如果<0,那么a>0,b<0”,
故答案为:如果<0,那么a>0,b<0.
13.解:作DF⊥BC于F,
∵CD是它的角平分线,DE⊥AC,DF⊥BC,
∴DF=DE=2,
∴△BCD的面积=×BC×DF=6(cm2),
故答案为:6.
14.解:∵DE是AC边上的垂直平分线,
∴DA=DC,
∴∠A=∠DCA,
∵CD平分∠ACB,
∴∠BCD=∠DCA,
∴∠A=∠DCA=∠BCD,
∵∠B=90°,
∴∠A=30°,
故答案为:30°.
15.解:∵∠BAC=80°,
∴∠B+∠C=180°﹣80°=100°,
∵DE、FG分别为AB、AC的垂直平分线,
∴EA=EB,FA=FC,
∴∠EAB=∠B,∠FAC=∠C,
∴∠EAB+∠FAC=∠B+∠C=100°,
∴∠EAF=∠EAB+∠FAC﹣∠BAC=100°﹣80°=20°,
故答案为:20°.
16.解:过点O作OE⊥AB于E,OF⊥AC与F,连接OA,
∵OB平分∠ABC,OD⊥BC,OE⊥AB,
∴OE=OD=1,
同理可知,OF=OD=1,
∴△ABC的面积=△OAB的面积+△OAC的面积+△OBC的面积
=×AB×OE+×AC×OF+×BC×OD
=×18×1
=9,
故答案为:9.
三.解答题
17.解:(1)同旁内角互补,两直线平行的逆命题是两直线平行,同旁内角互补,成立;
(2)如果两个角是直角,那么这两个角相等的逆命题是如果两个角相等、那么这两个角是直角,不成立.
18.(1)证明:∵EF∥CD(已知),
∴∠BEF=∠BCD(两直线平行,同位角相等),
∵∠B+∠BDG=180°(已知),
∴BC∥DG(同旁内角互补,两直线平行),
∴∠CDG=∠BCD(两直线平行,内错角相等),
∴∠BEF=∠CDG(等量代换);
(2)①条件:DG∥BC,∠B=∠BCD(答案不唯一),
结论:DG平分∠ADC,
②证明:∵DG∥BC,
∴∠ADG=∠B,∠CDG=∠BCD,
∵∠B=∠BCD,
∴∠ADG=∠CDG,即DG平分∠ADC.
故答案为:(1)∠BCD;两直线平行,同位角相等;DG;同旁内角互补,两直线平行;∠BCD;两直线平行,内错角相等;
(2)①、①③;②,
∵DG∥BC,
∴∠ADG=∠B,∠CDG=∠BCD,
∵∠B=∠BCD,
∴∠ADG=∠CDG,即DG平分∠ADC.
19.解:(1)如图1,作DF⊥AC于F,
∵AD是△ABC的角平分线,DE⊥AB,DF⊥AC,
∴DF=DE=3,
由题意得,×AB×3+×AC×3=20,
解得,AC=AB=;
(2)如图2,作DF⊥AC于F,
∵AD是△ABC的角平分线,DE⊥AB,DF⊥AC,
∴DF=DE=3,
由题意得,×5×3+×AC×3=20,
解得,AC=.
20.(1)解:如果①②,那么③;
如果①③,那么②;
如果②③,那么①;
(2)①已知:AD∥BC,∠B=∠C,求证:AD平分∠EAC;
证明:∵AD∥BC,
∴∠DAE=∠B,∠DAC=∠C,
∵∠B=∠C,
∴∠DAE=∠DAC,
∴AD平分∠EAC;
②已知:AD∥BC,AD平分∠EAC,
求证:∠B=∠C;
证明:∵AD∥BC,
∴∠DAE=∠B,∠DAC=∠C,
∵AD平分∠EAC,
∴∠DAE=∠DAC,
∴∠B=∠C;
③已知:∠B=∠C,AD平分∠EAC,
求证:AD∥BC;
证明:∵∠EAC=∠B+∠C,∠B=∠C,
∴∠EAC=2∠B,
∵AD平分∠EAC,
∴∠EAC=2∠EAD,
∴∠EAD=∠B,
∴AD∥BC.
故答案为:AD∥BC,∠B=∠C;
AD平分∠EAC;
∵AD∥BC,
∴∠DAE=∠B,∠DAC=∠C,
∵∠B=∠C,
∴∠DAE=∠DAC,
∴AD平分∠EAC.
21.解:(1)依据两点间的距离公式,可得AB==13;
(2)当点A,B在平行于y轴的直线上时,AB=|﹣1﹣5|=6;
(3)AB与AC相等.理由:
∵AB==5;
AC==5;
BC=|3﹣(﹣3)|=6.
∴AB=AC.
