2.6《有理数的加减混合运算》第3课时 课件 2021-2022学年北师大版数学七年级上册(19张)
文档属性
| 名称 | 2.6《有理数的加减混合运算》第3课时 课件 2021-2022学年北师大版数学七年级上册(19张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 387.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-29 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
第二章
有理数及其运算
2.6
有理数的加减混合运算
第3课时
学习目标
1.能将生活中的实际问题转化为有理数的加减混合运算;
2.熟练地进行有理数的加减混合运算,解决实际问题.
复习巩固
计算:
(1)2-7;
(2)
(-2)-7;
(3)(-2)-(-7);
(4)2+(-7)
(5)
;
(6)
;
(7)
探究新知
问题(1).下图是流花河的水文资料(单位:米).
1.取河流的警戒水位作为0,那么图中其他数据可以分别记作什么?
解:取河流的警戒水位(33.4
m)作为0点,那么图中的最高水位(35.3
m)可记作+1.9
m,平均水位(22.6
m)可记作-10.8
m,最低水位(11.5
m)可记作-21.9
m.
探究新知
问题(2).下表是小明记录的今年雨季流花河一周内的水位变化情况(上周末的水位达到警戒水位).
注:正号表示水位比前一天上升,负号表示水位比前一天下降.
星期
一
二
三
四
五
六
日
水位变化/米
+0.2
+0.81
-0.35
+0.03
+0.28
-0.36
-0.01
探究新知
(1)本周哪一天流花河的水位最高?哪一天水位最低?它们位于警戒水位之上还是之下?与警戒水位的距离分别是多少?
(2)与上周末相比,本周末流花河水位是上升了还是下降了?
解:(1)星期二的水位最高,星期一的水位最低,它们都位于警戒水位之上,与警戒水位的距离分别是:1.01
m,0.2
m.
(2)因为0.20+0.81-0.35+0.03+0.28-0.36-0.01=0.6(m).
所以本周末河流水位与上周末相比上升了.
星
期
一
二
三
四
五
六
日
水位记录(米)
33.6
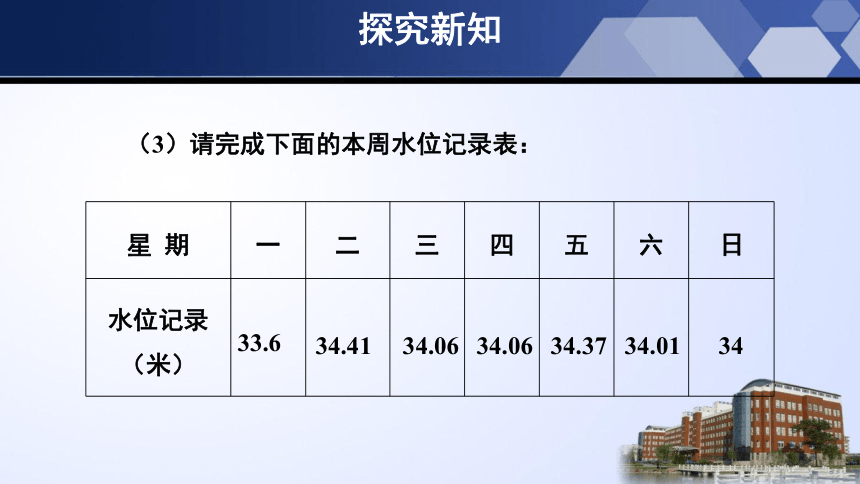
(3)请完成下面的本周水位记录表:
34.41
34.06
34.06
34.37
34.01
34
探究新知
(4)以警戒水位为0点,用折线统计图表示本周的水位情况.
解:如图所示.
水位/米
星期
日
六
五
四
三
二
一
日
1.0
0.8
0.6
0.4
0.2
探究新知
探究新知
问题3.某工厂一周计划每日生产自行车100辆,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的车辆数记为正数,减少的车辆数记为负数):
(1)生产量最多的一天比生产量最少的一天多生产多少辆?
(2)本周总生产量是多少?比原计划增加了还是减少了?增减数为多少?
星期
一
二
三
四
五
六
日
增减/辆
-1
+3
-2
+4
+7
-5
-10
探究新知
解析:(1)由表格找出生产量最多与最少的,相减即可得到结果;
(2)根据题意列出算式,计算即可得到结果.
解:(1)7-(-10)=17(辆);
(2)100×7+(-1+3-2+4+7-5-10)=696(辆),
答:(1)生产量最多的一天比生产量最少的一天多生产17辆;
(2)本周总生产量是696辆,比原计划减少了4辆.
典型例题
1.一辆公共汽车上原有20人,到站后下去了5人,又上来了8人,下一站下去6人,再上来9人,现在公共汽车上有______人.
2.黄山主峰一天早晨气温为-1
℃,中午上升了8
℃,夜间又下降了10
℃,那么这天夜间黄山主峰的气温是_________.
典型例题
3.已知有理数a、b、c在数轴上对应点分别为A、B、C,点A、B在数轴上的位置如图所示,若|b|=4,AC=2,则a+b-c=______
4.矿井下A、B、C三处的高度分别是-37.4m,-129.8m,-71.3m,A处比B处高多少米?C处比B处高多少米?A处比C处高多少米?
解:A处比B处高:-37.4-(-129.8)=92.4(m),
C处比B处高:-71.3-(-129.8)=58.5(m),
A处比C处高:-37.4-(-71.3)=33.9(m).
随堂练习
1.下表是某水库一周内水位高低的变化情况(用正数记水位比前一日上升数,用负数记下降数).那么本周星期几水位最低( )
A.星期二
B.星期四
C.星期六
D.星期五
2.一个数减去-5与2的和,所得的差是6,求该数的相反数.
解:根据题意知这个数为6+(-5+2)=6+(-3)=3,
所以这个数的相反数为-3.
星期
一
二
三
四
五
六
日
水位变化/米
0.12
-0.02
-0.13
-0.20
-0.08
-0.02
0.32
随堂练习
3.光明中学七(1)班学生的平均身高是160
cm.
(1)下表给出了该班6名学生的身高情况(单位:cm).试完成下表:
(2)这6名学生中谁最高?谁最矮?
(3)最高与最矮的学生身高相差多少?
姓名
小明
小彬
小丽
小亮
小颖
小山
身高
159
154
165
身高与平均身高的差值
-1
+2
0
+3
解:小山最高,小亮最矮.
最高与最矮的学生身高相差:165-154=11(cm).
随堂练习
4.有依次排列的3个数:3,9,8,对任意相邻的两个数,都用右边的数减去左边的数,所得之差写在这两个数之间,可产生一个新数串:3,6,9,-1,8,这称为第一次操作;第二次同样的操作后也可产生一个新数串:3,3,6,3,9,-10,-1,9,8;继续依次操作下去.问
(1)第一次操作后,增加的所有新数之和是多少?
(2)第二次操作后所得的新数串比第一次操作后所得的数串增加的所有新数之和是多少?
(3)猜想:第一百次操作后得到的新数串比第九十九次操作后所得的数串增加的所有新数之和是多少?
随堂练习
解:(1)第一次操作后增加的新数是6,-1,则6+(-1)=5.
(2)第二次操作后所得的新数串比第一次操作后所得的数串增加的所有新数之和为3+3+(-10)+9=5.
(3)猜想:第一百次操作后得到的新数串比第九十九次操作后所得的数串增加的所有新数之和为5.
课堂小结
1.本节课你学习了什么?
2.本节课你有哪些收获?
3.通过今天的学习,你想进一步探究的问题是什么?
1.通过学习本节内容,要能将生活中的问题转化为有理数的加减混合运算,使问题简单明了.
2.要特别注意正、负号的含义,含义不同,计算的过程和结果也都不相同.
3.计算时要注意:减法统一成加法时减号要变加号,减数变成相反数,统一成加法后才可以用加法的交换律和结合律.
课堂小结
再见
第二章
有理数及其运算
2.6
有理数的加减混合运算
第3课时
学习目标
1.能将生活中的实际问题转化为有理数的加减混合运算;
2.熟练地进行有理数的加减混合运算,解决实际问题.
复习巩固
计算:
(1)2-7;
(2)
(-2)-7;
(3)(-2)-(-7);
(4)2+(-7)
(5)
;
(6)
;
(7)
探究新知
问题(1).下图是流花河的水文资料(单位:米).
1.取河流的警戒水位作为0,那么图中其他数据可以分别记作什么?
解:取河流的警戒水位(33.4
m)作为0点,那么图中的最高水位(35.3
m)可记作+1.9
m,平均水位(22.6
m)可记作-10.8
m,最低水位(11.5
m)可记作-21.9
m.
探究新知
问题(2).下表是小明记录的今年雨季流花河一周内的水位变化情况(上周末的水位达到警戒水位).
注:正号表示水位比前一天上升,负号表示水位比前一天下降.
星期
一
二
三
四
五
六
日
水位变化/米
+0.2
+0.81
-0.35
+0.03
+0.28
-0.36
-0.01
探究新知
(1)本周哪一天流花河的水位最高?哪一天水位最低?它们位于警戒水位之上还是之下?与警戒水位的距离分别是多少?
(2)与上周末相比,本周末流花河水位是上升了还是下降了?
解:(1)星期二的水位最高,星期一的水位最低,它们都位于警戒水位之上,与警戒水位的距离分别是:1.01
m,0.2
m.
(2)因为0.20+0.81-0.35+0.03+0.28-0.36-0.01=0.6(m).
所以本周末河流水位与上周末相比上升了.
星
期
一
二
三
四
五
六
日
水位记录(米)
33.6
(3)请完成下面的本周水位记录表:
34.41
34.06
34.06
34.37
34.01
34
探究新知
(4)以警戒水位为0点,用折线统计图表示本周的水位情况.
解:如图所示.
水位/米
星期
日
六
五
四
三
二
一
日
1.0
0.8
0.6
0.4
0.2
探究新知
探究新知
问题3.某工厂一周计划每日生产自行车100辆,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的车辆数记为正数,减少的车辆数记为负数):
(1)生产量最多的一天比生产量最少的一天多生产多少辆?
(2)本周总生产量是多少?比原计划增加了还是减少了?增减数为多少?
星期
一
二
三
四
五
六
日
增减/辆
-1
+3
-2
+4
+7
-5
-10
探究新知
解析:(1)由表格找出生产量最多与最少的,相减即可得到结果;
(2)根据题意列出算式,计算即可得到结果.
解:(1)7-(-10)=17(辆);
(2)100×7+(-1+3-2+4+7-5-10)=696(辆),
答:(1)生产量最多的一天比生产量最少的一天多生产17辆;
(2)本周总生产量是696辆,比原计划减少了4辆.
典型例题
1.一辆公共汽车上原有20人,到站后下去了5人,又上来了8人,下一站下去6人,再上来9人,现在公共汽车上有______人.
2.黄山主峰一天早晨气温为-1
℃,中午上升了8
℃,夜间又下降了10
℃,那么这天夜间黄山主峰的气温是_________.
典型例题
3.已知有理数a、b、c在数轴上对应点分别为A、B、C,点A、B在数轴上的位置如图所示,若|b|=4,AC=2,则a+b-c=______
4.矿井下A、B、C三处的高度分别是-37.4m,-129.8m,-71.3m,A处比B处高多少米?C处比B处高多少米?A处比C处高多少米?
解:A处比B处高:-37.4-(-129.8)=92.4(m),
C处比B处高:-71.3-(-129.8)=58.5(m),
A处比C处高:-37.4-(-71.3)=33.9(m).
随堂练习
1.下表是某水库一周内水位高低的变化情况(用正数记水位比前一日上升数,用负数记下降数).那么本周星期几水位最低( )
A.星期二
B.星期四
C.星期六
D.星期五
2.一个数减去-5与2的和,所得的差是6,求该数的相反数.
解:根据题意知这个数为6+(-5+2)=6+(-3)=3,
所以这个数的相反数为-3.
星期
一
二
三
四
五
六
日
水位变化/米
0.12
-0.02
-0.13
-0.20
-0.08
-0.02
0.32
随堂练习
3.光明中学七(1)班学生的平均身高是160
cm.
(1)下表给出了该班6名学生的身高情况(单位:cm).试完成下表:
(2)这6名学生中谁最高?谁最矮?
(3)最高与最矮的学生身高相差多少?
姓名
小明
小彬
小丽
小亮
小颖
小山
身高
159
154
165
身高与平均身高的差值
-1
+2
0
+3
解:小山最高,小亮最矮.
最高与最矮的学生身高相差:165-154=11(cm).
随堂练习
4.有依次排列的3个数:3,9,8,对任意相邻的两个数,都用右边的数减去左边的数,所得之差写在这两个数之间,可产生一个新数串:3,6,9,-1,8,这称为第一次操作;第二次同样的操作后也可产生一个新数串:3,3,6,3,9,-10,-1,9,8;继续依次操作下去.问
(1)第一次操作后,增加的所有新数之和是多少?
(2)第二次操作后所得的新数串比第一次操作后所得的数串增加的所有新数之和是多少?
(3)猜想:第一百次操作后得到的新数串比第九十九次操作后所得的数串增加的所有新数之和是多少?
随堂练习
解:(1)第一次操作后增加的新数是6,-1,则6+(-1)=5.
(2)第二次操作后所得的新数串比第一次操作后所得的数串增加的所有新数之和为3+3+(-10)+9=5.
(3)猜想:第一百次操作后得到的新数串比第九十九次操作后所得的数串增加的所有新数之和为5.
课堂小结
1.本节课你学习了什么?
2.本节课你有哪些收获?
3.通过今天的学习,你想进一步探究的问题是什么?
1.通过学习本节内容,要能将生活中的问题转化为有理数的加减混合运算,使问题简单明了.
2.要特别注意正、负号的含义,含义不同,计算的过程和结果也都不相同.
3.计算时要注意:减法统一成加法时减号要变加号,减数变成相反数,统一成加法后才可以用加法的交换律和结合律.
课堂小结
再见
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
