13.3.1 等腰三角形 课件(共29张PPT)
文档属性
| 名称 | 13.3.1 等腰三角形 课件(共29张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-29 07:51:05 | ||
图片预览






文档简介
(共29张PPT)
人教版
八年级上
等腰三角形
1
经历探究、发现等腰三角形性质的过程
2
理解并掌握等腰三角形的性质
能运用等腰三角形的性质解决问题
能体会运用过程中的化归思想和方程思想
教学目标
教学重点
等腰三角形的性质的灵活运用
3
教学难点
等腰三角形性质的探究与推导
学习目标
建筑工人在盖房子时,用一块等腰三角板放在梁上,
从顶点系一重物,如果系重物的绳子正好经过三角板
底边中点,就说房梁是水平的,你知道为什么吗?
情景导入
等腰三角形
你知道什么样的三角形是等腰三角形吗?
温故知新
有两条边相等的三角形,叫做等腰三角形.
在△
ABC中,AB
=AC,则△
ABC是等腰三角形
等腰三角形的概念
温故知新
A
B
C
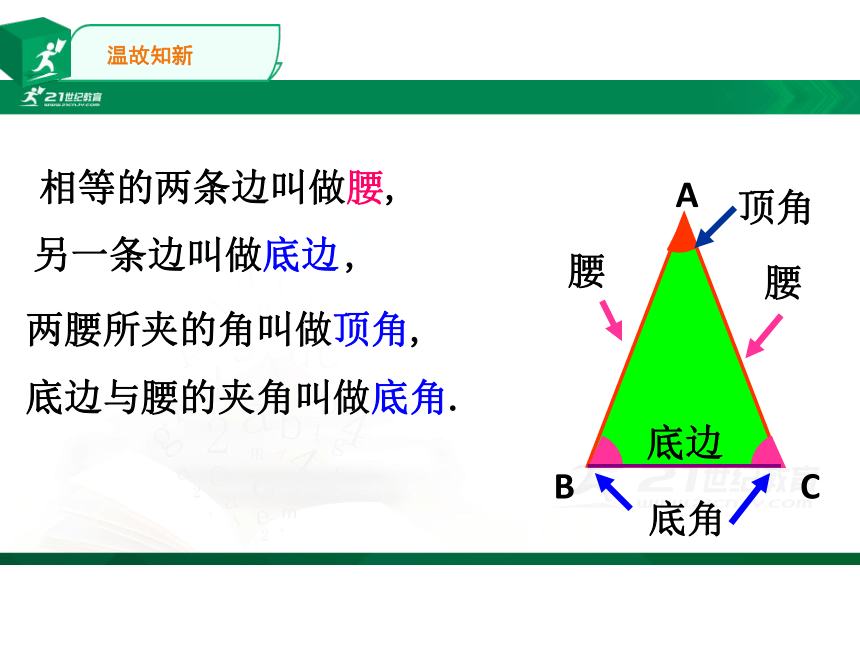
相等的两条边叫做腰,
另一条边叫做底边
,
底边与腰的夹角叫做底角.
两腰所夹的角叫做顶角,
腰
腰
底边
顶角
底角
温故知新
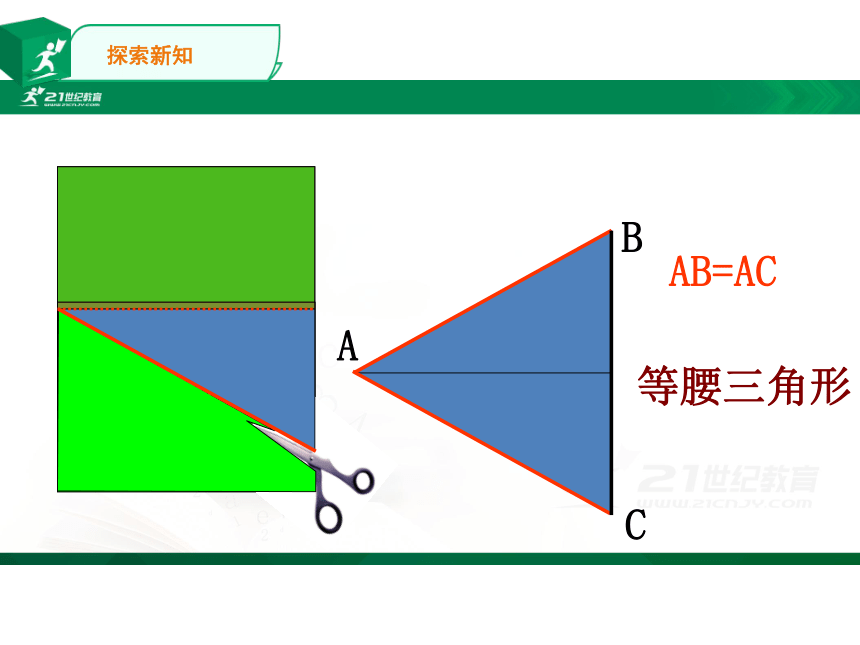
请同学们把准备好的长方形纸片按图中虚线对折,
,再把它展开,得到的△ABC有什么特点?
并剪去绿色部分
探索新知
A
B
C
AB=AC
等腰三角形
探索新知
刚才剪出的等腰三角形是轴对称图形吗?
通过观察,请找出其中重合的线段和角,填入下表:
探索新知
A
B
C
D
重合的线段
重合的角
由这些重合的线段和角,你能发现等腰三角形除了两腰相等以外,还有其他的性质吗?
AB
=
AC
BD
=
CD
AD
=
AD
∠B
=∠C
∠ADB
=∠ADC
∠BAD
=∠CAD
等腰△ABC是轴对称图形
观察猜想
A
B
C
D
等腰△ABC还有哪些性质?
相等的角:
①
∠B
=
∠C
②
∠BAD
=∠CAD
③
∠ADC
=∠ADB=900
相等的边:
④
BD
=
CD
→
两个底角相等
→
AD为顶角∠BAC的平分线
→
AD为底边BC
上的高
→
AD为底边BC
上的中线
等腰三角形性质
性质1
等腰三角形的两个底角相等(简写成“等边对等角”)
性质2
等腰三角形的顶角平分线、底边上的中线、
底边上的高互相重合(可简记为“三线合一”)
通过刚才的操作与观察,我们得出以下结论:
深思熟虑
等腰三角形的两个底角相等
已知:△ABC中,AB=AC
求证:?B=?C
,△
ABC的顶角平分线、
底边上的中线、底边上的高互相重合.
分析:1.如何证明两个角相等?
2.如何构造两个全等的三角形?
求证:
A
B
C
D
等腰三角形的“三线合一”
推理论证
证明:
作顶角∠
BAD的平分线AD,则有∠1=∠2
AB=AC
∠
1=
∠
2
AD=AD
∴△BAD
≌△CAD
(SAS)
∴∠
B
=
∠C
,BD=CD,
∠
BDA
=
∠CDA=90
°
已知:
△
ABC中,AB
=AC.
求证:
∠B
=
∠C,△
ABC的顶角平分线、
底边上的中线、底边上的高互相重合.
A
B
C
1
2
作顶角的平分线
D
在△BAD和△CAD中,
推理论证
证明:
作底边BC上的中线AD,则BD=CD
AB=AC
BD=CD
AD=AD
∴△BAD
≌△CAD
(SSS)
∴∠
B=
∠C,
∠
BAD
=
∠CAD,
∠
BDA
=
∠CDA=90
°
A
B
C
D
作底边上的中线
在△BAD和△CAD中,
已知:
△
ABC中,AB
=AC.
求证:
∠B
=
∠C,△
ABC的顶角平分线、
底边上的中线、底边上的高互相重合.
推理论证
证明:
作底边BC上的高线AD,则有
∠ADB=∠ADC
=90?
AB=AC
AD=AD
∴Rt
△BAD
≌Rt
△CAD
(HL)
∴
∠
B
=
∠C,
∠
BAD
=
∠CAD,
BD=CD
A
B
C
D
作底边上的高线
在Rt△BAD和Rt△CAD中
已知:
△
ABC中,AB
=AC.
求证:
∠B
=
∠C,△
ABC的顶角平分线、
底边上的中线、底边上的高互相重合.
推理论证
等腰三角形的性质
等腰三角形的两个底角相等
性质1
(等边对等角)
A
B
C
数学符号语言
在△ABC中
∵
AB=AC
∴
∠B=∠C
得出结论
性质2
A
B
C
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合
(等腰三角形的“三线合一”)
D
等腰三角形的性质
得出结论
知一线得二线
“三线合一”可以帮助我们解决线段的垂直、相等
以及角的相等问题.
数学符号语言
在△ABC中,
A
B
C
D
得出结论
(1)∵AB=AC
,
AD⊥BC
∴∠
=∠
,
=
;
(2)∵AB=AC
,
BD=CD
∴
⊥
,
∠
=∠
;
(3)∵
AB=AC
,
∠BAD=∠CAD
∴
⊥
,
=
.
A
B
C
D
BAD
CAD
BD
CD
BAD
CAD
AD
BC
AD
BC
BD
CD
得出结论
D
如图,作△ABC底边上的中线AD
D
D
如图,作顶角的平分线AD
A
B
C
A
B
C
A
B
C
等腰三角形常见辅助线
△
ABC中,AB=AC
归纳小结
如图,作△ABC底边上的高AD
建筑工人在盖房子时,用一块等腰三角板放在梁上,
从顶点系一重物,如果系重物的绳子正好经过三角板
底边中点,就说房梁是水平的,你现在知道为什么吗?
解决问题
例1
如图,在△ABC中
,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数.
1、图中有哪几个等腰三角形?
A
B
C
D
△ABC
,
△ABD
,△BDC
2、有哪些相等的角?
∠ABC=∠ACB=∠BDC
,
∠
A=∠ABD
3、这两组相等的角之间还有什么关系?
∠BDC=2∠
A
∠ABC+
∠ACB+
∠A=180
°
例题精讲
如图,在△ABC中
,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数.
A
B
C
D
x
⌒
2x
⌒
2x
⌒
⌒
2x
解:∵AB
=
AC,BD
=
BC=
AD,
∴∠ABC
=∠C
=∠BDC,∠A
=∠ABD
(等边对等角)
设∠A=x,
于是在△ABC中,有∠A+∠ABC+∠C=x+2x+2x=180°
解得x=36°
在△ABC中,
∠A=36°,
∠ABC=∠C=72°
则∠BDC
=∠A+∠ABD
=2x,
从而∠ABC
=
∠C
=
∠BDC
=2x,
例题精讲
1、等腰三角形一个底角为80°,它的顶角为______
2、等腰三角形一个角为80°,它的另外两个角为
__________________
3、等腰三角形一个外角为110°,它的顶角为__________
20°
80
°,
20°或50
°,
50°
70
°
或40°
4、如图,在△ABC中,AB=AC,∠BAC=100°,AB的垂直平分线DE分别交AB、BC于点D、E,则∠AED=(
)
A.80°
B.60°
C.50°
D.40°
C
巩固练习
如图,在△ABC中,AB=AC,AD是BC边上的中线,
∠ABC的平分线BG交AC于点G,交AD于点E,EF⊥AB于F.
(1)若∠BAD=25°,求∠C的度数
(2)求证:EF=ED
巩固练习
又∵BG平分∠ABC,EF⊥AB
∴
EF=ED
(1)解:∵AB=AC,AD是BC边上的中线
∴∠BAD=∠CAD=25
°
∴∠BAC=2∠BAD=50°
∵AB=AC
∴∠C=∠ABC
=
(180°-∠
BAC
)
÷2
=
(180°-
50°)
÷2
=65°
(2)证明:∵AB=AC,AD是BC边上的中线
∴ED⊥BC
巩固练习
(1)等腰三角形是轴对称图形
(2)等腰三角形的两个底角相等(简称
“等边对等角”)
(3)等腰三角形顶角平分线、底边上的中线,底边上的高互相重合(简称“三线合一”)
等腰三角形
2、本节课学习了数学思想方法:
分类讨论、方程思想、转化思想.
1、本节课主要教学内容是等腰三角形的性质:
课堂小结
https://www.21cnjy.com/help/help_extract.php
人教版
八年级上
等腰三角形
1
经历探究、发现等腰三角形性质的过程
2
理解并掌握等腰三角形的性质
能运用等腰三角形的性质解决问题
能体会运用过程中的化归思想和方程思想
教学目标
教学重点
等腰三角形的性质的灵活运用
3
教学难点
等腰三角形性质的探究与推导
学习目标
建筑工人在盖房子时,用一块等腰三角板放在梁上,
从顶点系一重物,如果系重物的绳子正好经过三角板
底边中点,就说房梁是水平的,你知道为什么吗?
情景导入
等腰三角形
你知道什么样的三角形是等腰三角形吗?
温故知新
有两条边相等的三角形,叫做等腰三角形.
在△
ABC中,AB
=AC,则△
ABC是等腰三角形
等腰三角形的概念
温故知新
A
B
C
相等的两条边叫做腰,
另一条边叫做底边
,
底边与腰的夹角叫做底角.
两腰所夹的角叫做顶角,
腰
腰
底边
顶角
底角
温故知新
请同学们把准备好的长方形纸片按图中虚线对折,
,再把它展开,得到的△ABC有什么特点?
并剪去绿色部分
探索新知
A
B
C
AB=AC
等腰三角形
探索新知
刚才剪出的等腰三角形是轴对称图形吗?
通过观察,请找出其中重合的线段和角,填入下表:
探索新知
A
B
C
D
重合的线段
重合的角
由这些重合的线段和角,你能发现等腰三角形除了两腰相等以外,还有其他的性质吗?
AB
=
AC
BD
=
CD
AD
=
AD
∠B
=∠C
∠ADB
=∠ADC
∠BAD
=∠CAD
等腰△ABC是轴对称图形
观察猜想
A
B
C
D
等腰△ABC还有哪些性质?
相等的角:
①
∠B
=
∠C
②
∠BAD
=∠CAD
③
∠ADC
=∠ADB=900
相等的边:
④
BD
=
CD
→
两个底角相等
→
AD为顶角∠BAC的平分线
→
AD为底边BC
上的高
→
AD为底边BC
上的中线
等腰三角形性质
性质1
等腰三角形的两个底角相等(简写成“等边对等角”)
性质2
等腰三角形的顶角平分线、底边上的中线、
底边上的高互相重合(可简记为“三线合一”)
通过刚才的操作与观察,我们得出以下结论:
深思熟虑
等腰三角形的两个底角相等
已知:△ABC中,AB=AC
求证:?B=?C
,△
ABC的顶角平分线、
底边上的中线、底边上的高互相重合.
分析:1.如何证明两个角相等?
2.如何构造两个全等的三角形?
求证:
A
B
C
D
等腰三角形的“三线合一”
推理论证
证明:
作顶角∠
BAD的平分线AD,则有∠1=∠2
AB=AC
∠
1=
∠
2
AD=AD
∴△BAD
≌△CAD
(SAS)
∴∠
B
=
∠C
,BD=CD,
∠
BDA
=
∠CDA=90
°
已知:
△
ABC中,AB
=AC.
求证:
∠B
=
∠C,△
ABC的顶角平分线、
底边上的中线、底边上的高互相重合.
A
B
C
1
2
作顶角的平分线
D
在△BAD和△CAD中,
推理论证
证明:
作底边BC上的中线AD,则BD=CD
AB=AC
BD=CD
AD=AD
∴△BAD
≌△CAD
(SSS)
∴∠
B=
∠C,
∠
BAD
=
∠CAD,
∠
BDA
=
∠CDA=90
°
A
B
C
D
作底边上的中线
在△BAD和△CAD中,
已知:
△
ABC中,AB
=AC.
求证:
∠B
=
∠C,△
ABC的顶角平分线、
底边上的中线、底边上的高互相重合.
推理论证
证明:
作底边BC上的高线AD,则有
∠ADB=∠ADC
=90?
AB=AC
AD=AD
∴Rt
△BAD
≌Rt
△CAD
(HL)
∴
∠
B
=
∠C,
∠
BAD
=
∠CAD,
BD=CD
A
B
C
D
作底边上的高线
在Rt△BAD和Rt△CAD中
已知:
△
ABC中,AB
=AC.
求证:
∠B
=
∠C,△
ABC的顶角平分线、
底边上的中线、底边上的高互相重合.
推理论证
等腰三角形的性质
等腰三角形的两个底角相等
性质1
(等边对等角)
A
B
C
数学符号语言
在△ABC中
∵
AB=AC
∴
∠B=∠C
得出结论
性质2
A
B
C
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合
(等腰三角形的“三线合一”)
D
等腰三角形的性质
得出结论
知一线得二线
“三线合一”可以帮助我们解决线段的垂直、相等
以及角的相等问题.
数学符号语言
在△ABC中,
A
B
C
D
得出结论
(1)∵AB=AC
,
AD⊥BC
∴∠
=∠
,
=
;
(2)∵AB=AC
,
BD=CD
∴
⊥
,
∠
=∠
;
(3)∵
AB=AC
,
∠BAD=∠CAD
∴
⊥
,
=
.
A
B
C
D
BAD
CAD
BD
CD
BAD
CAD
AD
BC
AD
BC
BD
CD
得出结论
D
如图,作△ABC底边上的中线AD
D
D
如图,作顶角的平分线AD
A
B
C
A
B
C
A
B
C
等腰三角形常见辅助线
△
ABC中,AB=AC
归纳小结
如图,作△ABC底边上的高AD
建筑工人在盖房子时,用一块等腰三角板放在梁上,
从顶点系一重物,如果系重物的绳子正好经过三角板
底边中点,就说房梁是水平的,你现在知道为什么吗?
解决问题
例1
如图,在△ABC中
,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数.
1、图中有哪几个等腰三角形?
A
B
C
D
△ABC
,
△ABD
,△BDC
2、有哪些相等的角?
∠ABC=∠ACB=∠BDC
,
∠
A=∠ABD
3、这两组相等的角之间还有什么关系?
∠BDC=2∠
A
∠ABC+
∠ACB+
∠A=180
°
例题精讲
如图,在△ABC中
,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数.
A
B
C
D
x
⌒
2x
⌒
2x
⌒
⌒
2x
解:∵AB
=
AC,BD
=
BC=
AD,
∴∠ABC
=∠C
=∠BDC,∠A
=∠ABD
(等边对等角)
设∠A=x,
于是在△ABC中,有∠A+∠ABC+∠C=x+2x+2x=180°
解得x=36°
在△ABC中,
∠A=36°,
∠ABC=∠C=72°
则∠BDC
=∠A+∠ABD
=2x,
从而∠ABC
=
∠C
=
∠BDC
=2x,
例题精讲
1、等腰三角形一个底角为80°,它的顶角为______
2、等腰三角形一个角为80°,它的另外两个角为
__________________
3、等腰三角形一个外角为110°,它的顶角为__________
20°
80
°,
20°或50
°,
50°
70
°
或40°
4、如图,在△ABC中,AB=AC,∠BAC=100°,AB的垂直平分线DE分别交AB、BC于点D、E,则∠AED=(
)
A.80°
B.60°
C.50°
D.40°
C
巩固练习
如图,在△ABC中,AB=AC,AD是BC边上的中线,
∠ABC的平分线BG交AC于点G,交AD于点E,EF⊥AB于F.
(1)若∠BAD=25°,求∠C的度数
(2)求证:EF=ED
巩固练习
又∵BG平分∠ABC,EF⊥AB
∴
EF=ED
(1)解:∵AB=AC,AD是BC边上的中线
∴∠BAD=∠CAD=25
°
∴∠BAC=2∠BAD=50°
∵AB=AC
∴∠C=∠ABC
=
(180°-∠
BAC
)
÷2
=
(180°-
50°)
÷2
=65°
(2)证明:∵AB=AC,AD是BC边上的中线
∴ED⊥BC
巩固练习
(1)等腰三角形是轴对称图形
(2)等腰三角形的两个底角相等(简称
“等边对等角”)
(3)等腰三角形顶角平分线、底边上的中线,底边上的高互相重合(简称“三线合一”)
等腰三角形
2、本节课学习了数学思想方法:
分类讨论、方程思想、转化思想.
1、本节课主要教学内容是等腰三角形的性质:
课堂小结
https://www.21cnjy.com/help/help_extract.php
