人教版八年级上册 11.2.1 第1课时 三角形的内角和(共19张)
文档属性
| 名称 | 人教版八年级上册 11.2.1 第1课时 三角形的内角和(共19张) |  | |
| 格式 | zip | ||
| 文件大小 | 400.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-29 18:05:07 | ||
图片预览




文档简介
(共19张PPT)
11.2.1
三角形的内角
第十一章
三角形
11.2
与三角形有关的角
第1课时
三角形的内角和
学习目标
2.会运用三角形内角和定理进行计算.(难点)
1.会用平行线的性质与平角的定义证明三角形内
角和等于180°.(重点)
温故旧知
知识点一:平行线的性质1
平行线的性质1
文字语言:两直线平行,同位角
.?
图示:(“F”字形)
几何语言:
∵
,?
∴
.?
∠1=∠2
a∥b
相等
几何语言:
∵
,?
∴
.?
∠1=∠2
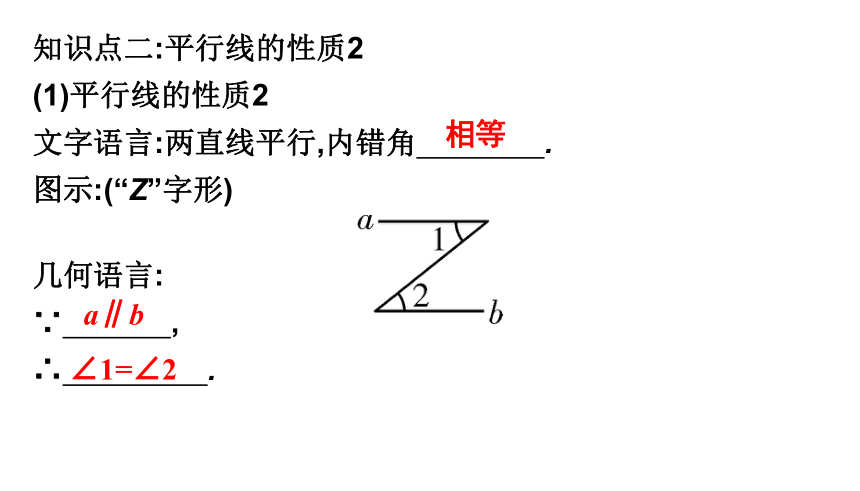
知识点二:平行线的性质2
(1)平行线的性质2
文字语言:两直线平行,内错角
.?
图示:(“Z”字形)
a∥b
相等
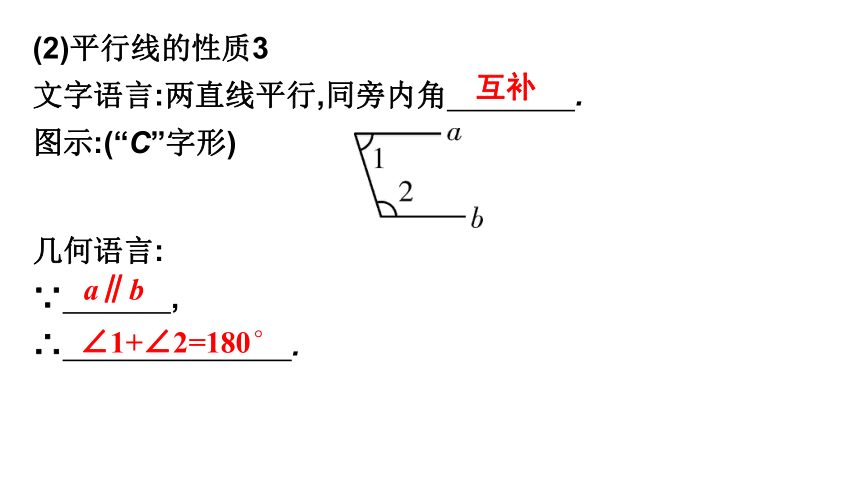
(2)平行线的性质3
文字语言:两直线平行,同旁内角
.?
图示:(“C”字形)
几何语言:
∵
,?
∴
.?
∠1+∠2=180°
a∥b
互补
我的形状最小,那我的内角和最小.
我的形状最大,那我的内角和最大.
不对,我有一个钝角,所以我的内角和才是最大的.
一天,三类三角形通过对自身的特点,讲出了自己对三角形内角和的理解,请同学们作为小判官给它们评判一下吧.
情境引入
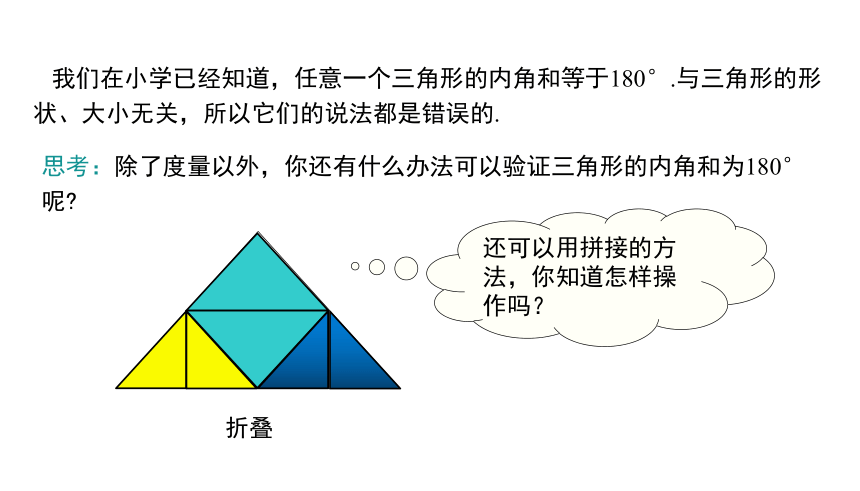
我们在小学已经知道,任意一个三角形的内角和等于180°.与三角形的形状、大小无关,所以它们的说法都是错误的.
思考:除了度量以外,你还有什么办法可以验证三角形的内角和为180°呢?
折叠
还可以用拼接的方法,你知道怎样操作吗?
三角形的三个内角拼到一起恰好构成一个平角.
观测的结果不一定可靠,还需要通过数学知识来说明.从上面的操作过程,你能发现证明的思路吗?
还有其他的拼接方法吗?
三角形的内角和定理的证明
一
探究:在纸上任意画一个三角形,将它的内角剪下拼合在一起.
验证结论
三角形三个内角的和等于180°.
求证:∠A+∠B+∠C=180°.
已知:△ABC.
证法1:过点A作l∥BC,
∴∠B=∠1.
(两直线平行,内错角相等)
∠C=∠2.
(两直线平行,内错角相等)
∵∠2+∠1+∠BAC=180°(平角定义)∴∠B+∠C+∠BAC=180°(等量代换)
1
2
证法2:延长BC到D,过点C作CE∥BA,
∴
∠A=∠1
.
(两直线平行,内错角相等)
∠B=∠2.
(两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°,
∴∠A+∠B+∠ACB=180°.
C
B
A
E
D
1
2
思考:多种方法证明三角形内角和等于180°的核心是什么?
借助平行线的“移角”的功能,将三个角转化成一个平角.
C
A
B
1
2
3
4
5
l
A
B
C
D
E
知识要点
在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线.在平面几何里,辅助线通常画成虚线.
思路总结
为了证明三个角的和为180°,转化为一个平角或同旁内角互补等,这种转化思想是数学中的常用方法.
作辅助线
180
105°
70°
30
45
60
5.如图,直线l1∥l2,∠1=40°,∠2=65°,则∠3=________.
75
P12例1
如图,在△ABC中,
∠BAC=40
°,
∠B=75
°,AD是△ABC的角平分线,求∠ADB的度数.
A
B
C
D
解:由∠BAC=40
°,
AD是△ABC的角平分线,得
∠BAD=
∠BAC=20
°.
在△ABD中,
∠ADB=180°-∠B-∠BAD
=180°-75°-20°
=85°.
三角形的内角和定理的运用
二
1.平行线的性质与平角的定义证明三角形内角和等于180°
2.运用三角形内角和定理进行计算
小结
1.如图,AD⊥BC,∠1=∠2,∠C=65°,求∠BAC的度数.
2.求出下列各图中的x值.
谢谢!
11.2.1
三角形的内角
第十一章
三角形
11.2
与三角形有关的角
第1课时
三角形的内角和
学习目标
2.会运用三角形内角和定理进行计算.(难点)
1.会用平行线的性质与平角的定义证明三角形内
角和等于180°.(重点)
温故旧知
知识点一:平行线的性质1
平行线的性质1
文字语言:两直线平行,同位角
.?
图示:(“F”字形)
几何语言:
∵
,?
∴
.?
∠1=∠2
a∥b
相等
几何语言:
∵
,?
∴
.?
∠1=∠2
知识点二:平行线的性质2
(1)平行线的性质2
文字语言:两直线平行,内错角
.?
图示:(“Z”字形)
a∥b
相等
(2)平行线的性质3
文字语言:两直线平行,同旁内角
.?
图示:(“C”字形)
几何语言:
∵
,?
∴
.?
∠1+∠2=180°
a∥b
互补
我的形状最小,那我的内角和最小.
我的形状最大,那我的内角和最大.
不对,我有一个钝角,所以我的内角和才是最大的.
一天,三类三角形通过对自身的特点,讲出了自己对三角形内角和的理解,请同学们作为小判官给它们评判一下吧.
情境引入
我们在小学已经知道,任意一个三角形的内角和等于180°.与三角形的形状、大小无关,所以它们的说法都是错误的.
思考:除了度量以外,你还有什么办法可以验证三角形的内角和为180°呢?
折叠
还可以用拼接的方法,你知道怎样操作吗?
三角形的三个内角拼到一起恰好构成一个平角.
观测的结果不一定可靠,还需要通过数学知识来说明.从上面的操作过程,你能发现证明的思路吗?
还有其他的拼接方法吗?
三角形的内角和定理的证明
一
探究:在纸上任意画一个三角形,将它的内角剪下拼合在一起.
验证结论
三角形三个内角的和等于180°.
求证:∠A+∠B+∠C=180°.
已知:△ABC.
证法1:过点A作l∥BC,
∴∠B=∠1.
(两直线平行,内错角相等)
∠C=∠2.
(两直线平行,内错角相等)
∵∠2+∠1+∠BAC=180°(平角定义)∴∠B+∠C+∠BAC=180°(等量代换)
1
2
证法2:延长BC到D,过点C作CE∥BA,
∴
∠A=∠1
.
(两直线平行,内错角相等)
∠B=∠2.
(两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°,
∴∠A+∠B+∠ACB=180°.
C
B
A
E
D
1
2
思考:多种方法证明三角形内角和等于180°的核心是什么?
借助平行线的“移角”的功能,将三个角转化成一个平角.
C
A
B
1
2
3
4
5
l
A
B
C
D
E
知识要点
在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线.在平面几何里,辅助线通常画成虚线.
思路总结
为了证明三个角的和为180°,转化为一个平角或同旁内角互补等,这种转化思想是数学中的常用方法.
作辅助线
180
105°
70°
30
45
60
5.如图,直线l1∥l2,∠1=40°,∠2=65°,则∠3=________.
75
P12例1
如图,在△ABC中,
∠BAC=40
°,
∠B=75
°,AD是△ABC的角平分线,求∠ADB的度数.
A
B
C
D
解:由∠BAC=40
°,
AD是△ABC的角平分线,得
∠BAD=
∠BAC=20
°.
在△ABD中,
∠ADB=180°-∠B-∠BAD
=180°-75°-20°
=85°.
三角形的内角和定理的运用
二
1.平行线的性质与平角的定义证明三角形内角和等于180°
2.运用三角形内角和定理进行计算
小结
1.如图,AD⊥BC,∠1=∠2,∠C=65°,求∠BAC的度数.
2.求出下列各图中的x值.
谢谢!
