2021-2022学年人教版数学七年级上册2.2 整式的加减 课件(第3课时 37张)
文档属性
| 名称 | 2021-2022学年人教版数学七年级上册2.2 整式的加减 课件(第3课时 37张) |  | |
| 格式 | zip | ||
| 文件大小 | 444.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-29 16:21:34 | ||
图片预览






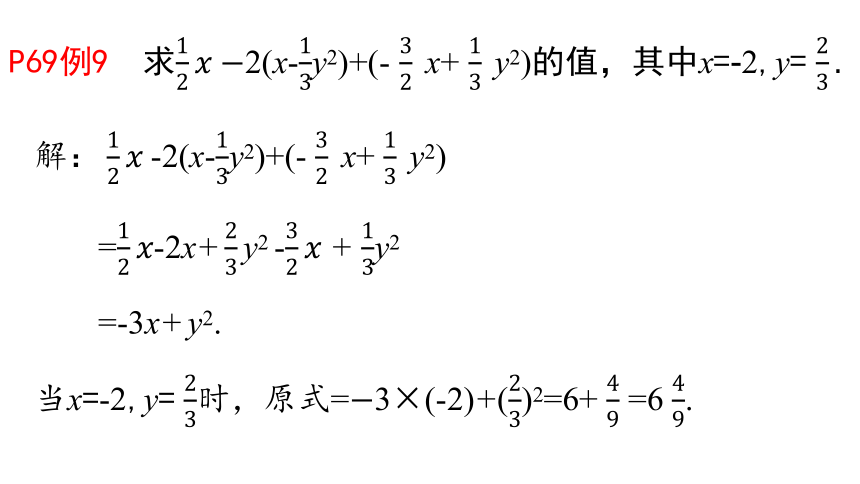

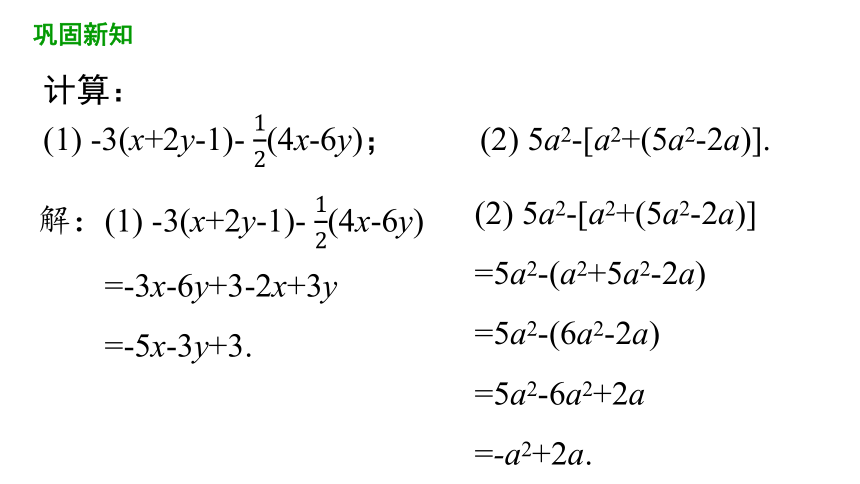


文档简介
(共37张PPT)
2.2
整式的加减
人教版·
数学·
七年级(上)
第二章
整式的加减
第3课时
整式的加减
1.能熟练进行整式的加减运算。(重点)
2.能利用整式的加减解决实际问题。(难点)
学习目标
任意写一个两位数,交换它的十位数字与个位数字,又得到一个数,两个数相加,重复几次看看.这些和有什么规律?对于任意一个两位数都成立吗?
导入新知
交换这个两位数的十位数字和个位数字,得到的数是
.
(10a+b)+(10b+a)=10a+b+10b+a=11a+11b=11(a+b)
10b+a
结论:这些和都是11的倍数.
如果用a,b分别表示一个两位数的十位数字和个位数字,那么这个两位数可以表示为
.
10a+b
.
将这两个数相加,得
P67例6
计算:
(1)
(2x-3y)+(5x+4y)
;
(2)
(8a-7b)-(4a-5b).
分析:第(1)题是计算多项式2x
-3y和5x+4y的和;
第(2)题是计算多项式8a-7b和4a-5b的差.
解:(1)原式=
2x-3y
+5x+4y
=
7x+y.
(2)
原式=
8a-7b-4a+5b
=4a-2b.
新知一
整式的加减
合作探究
整式加减的运算法则:
一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项.
注意:(1)
整式加减的结果要最简:①不能有同类项;②含字母项的系数不能出现带分数,带分数要化成假分数;③一般不含括号.
(2)
整式加减的结果如果是多项式,一般按照某一字母的升幂或降幂排列.
P69例9
求2(x-y2)+(-
x+
y2)的值,其中x=-2,y=
解-2(x-y2)+(-
x+
y2)
=-2x+
y2
-
+
y2
=-3x+
y2.
当x=-2,y=
时,原式=3×(-2)+()2=6+
=6
.
整式的化简求值以整式的加减运算为基础,具体步骤如下:
一化:利用整式加减的运算法则将整式化简;
二代:把已知字母或某个整式的值代入化简后的式子;
三计算:依据有理数的运算法则进行计算.
计算:
(1)
-3(x+2y-1)-
(4x-6y);
(2)
5a2-[a2+(5a2-2a)].
解:(1)
-3(x+2y-1)-
(4x-6y)
=-3x-6y+3-2x+3y
=-5x-3y+3.
(2)
5a2-[a2+(5a2-2a)]
=5a2-(a2+5a2-2a)
=5a2-(6a2-2a)
=5a2-6a2+2a
=-a2+2a.
巩固新知
P68例7
笔记本的单价是x元,圆珠笔的单价是y元.小红买3本笔记本,2
支圆珠笔;小明买4本笔记本,3支圆珠笔.买这些笔记本和圆珠笔,小红和小明一共花费多少钱?
解:方法1
小红买笔记本和圆珠笔共花费(3x+2y)元,
小明买笔记本和圆珠笔共花费(4x+3y)元.
小红和小明一共花费(单位:元)
(3x+2y)
+(4x+3y)=3x+2y+4x+3y
=
7x+5y.
新知二
利用整式的加减解决实际问题
合作探究
方法2
小红和小明买笔记本共花费(3x+4x)元,
圆珠笔共花费(2y+3y)元.
小红和小明一共花费(单位:元)
(3x+4x)
+
(2y+3y)
=
7x+5y.
P68例7
笔记本的单价是x元,圆珠笔的单价是y元.小红买3本笔记本,2
支圆珠笔;小明买4本笔记本,3支圆珠笔.买这些笔记本和圆珠笔,小红和小明一共花费多少钱?
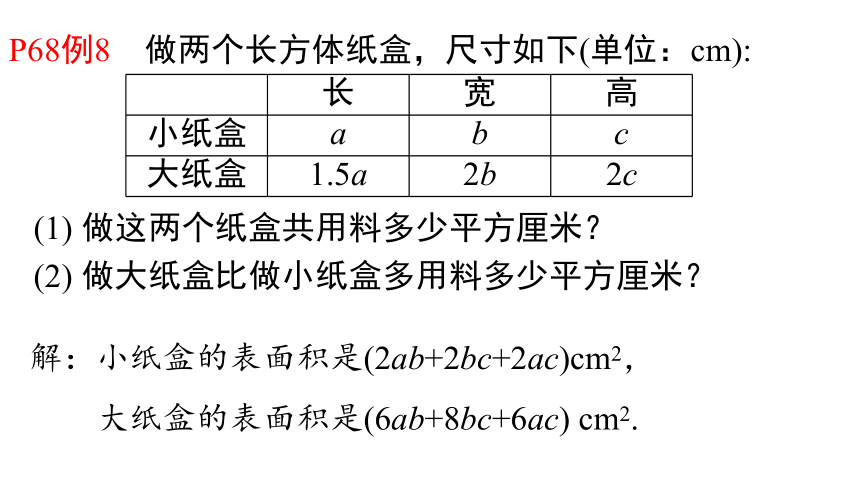
P68例8
做两个长方体纸盒,尺寸如下(单位:cm):
长
宽
高
小纸盒
a
b
c
大纸盒
1.5a
2b
2c
解:小纸盒的表面积是(2ab+2bc+2ac)cm2,
大纸盒的表面积是(6ab+8bc+6ac)
cm2.
(1)
做这两个纸盒共用料多少平方厘米?
(2)
做大纸盒比做小纸盒多用料多少平方厘米?
P68例8
做两个长方体纸盒,尺寸如下(单位:cm):
长
宽
高
小纸盒
a
b
c
大纸盒
1.5a
2b
2c
(1)
做这两个纸盒共用料多少平方厘米?
(2)
做大纸盒比做小纸盒多用料多少平方厘米?
(1)做这两个纸盒共用料(单位:cm2)
(2ab+2bc+2ac)+(6ab+8bc+6ac)
=8ab
+10bc+8ac.
(2)做大纸盒比做小纸盒多用料(单位:cm2)
(6ab+8bc+6ac)-(2ab+2bc+2ac)=4ab+6bc+4ac.
例8
做两个长方体纸盒,尺寸如下(单位:cm):
长
宽
高
小纸盒
a
b
c
大纸盒
1.5a
2b
2c
(1)
做这两个纸盒共用料多少平方厘米?
(2)
做大纸盒比做小纸盒多用料多少平方厘米?
1.一列火车上原有乘客(6a-2b)人,中途有一半乘客下车,又有若干乘客上车,此时车上共有乘客(10a-6b)人.试问:
中途上车的乘客有多少人?
当a=200,b=100时,中途上车的乘客有多少人?
有关整式加减的实际问题,应先根据题目中的数量关系,正确列出关系式,再按照整式加减的运算法则计算出最后结果
巩固新知
解:(1)根据题意,得
(10a-6b)-
(6a-2b)
=7a-5b.
故中途上车的乘客有(7a-5b)人.
(2)当a=200,b=100时,
7a-5b=7×200-5×100=1
400-500=900.
故中途上车的乘客有900人.
20
2.观察下图:
它们是按一定规律排列的,依照此规律,第9个图中共有
颗★.
列表:
1
2
3
4
…
9
n
4
6
8
10
…
20
2n+2
1.已知多项式2x2-x3+x与另一个多项式的和是x3+3x2-2x,求另一个多项式.
解:由题意,得x3+3x2
-2x-(2x2
–x3+x)
=x3+3x2-2x-2x2+x3-x
=2x3+x2-3x.
所以另一个多项式为2x3+x2-3x.
课堂练习
2.已知A=x2-2xy,B=y2+3xy,求2A-3B的值.
解:2A-3B=2(x2-2xy)-3(y2+3xy)
=2x2-4xy-3y2-9xy
=2x2-13xy-
3y2.
易错警示:A,B表示的多项式分别是一个整体,代入2A-3B时需要加括号.
3.先化简,再求值:a+2(2a-b)-3(a-b),其中a=-3,b=2.
解:a+2(2a-b)-3(a-b)
=a+4a-3b-3a+3b
=2a.
当a=-3时,原式=2×(-3)=-6.
将数值带入化简后的式子时,若数值是负数,要加上括号
整式化简求值的方法
一化:利用整式加减的运算法则将整式化简;
二代:把已知字母或某个整式的值代入化简后的式子;
三计算:依据有理数的运算法则进行计算.
归纳新知
D
C
课后练习
3.当x=2时,(x2-x)-2(x2-x-1)的值为(
)
A.-4
B.0
C.1
D.4
4.已知A=a2+b2-c2,B=-4a2+2b2+3c2,
若A+B+C=0,则多项式C为(
)
A.5a2+3b2+2c2
B.5a2-3b2+4c2
C.3a2-3b2-2c2
D.3a2+3b2+4c2
B
C
5.比x2+4x+3少5x2-2x+7的多项式是_______________.
6.一个式子减去-2x得-2x2-2x+1,则这个式子为___________.
-4x2+6x-4
-2x2-4x+1
7.计算:
(1)(9x-6y)-(5x-4y);
解:原式=9x-6y-5x+4y=4x-2y.
(2)(x2-y2)-3(x2-2y2);
解:原式=x2-y2-3x2+6y2=-2x2+5y2.
(3)(9a-2b)-[8a-(5b-2a)]+2c.
解:原式=9a-2b-(8a-5b+2a)+2c=
9a-2b-8a+5b-2a+2c=-a+3b+2c.
8.已知A=3x2-2xy+y2,B=2x2+3xy-4y2,求:
(1)A-2B;
(2)2A+B.
解:(1)A-2B=(3x2-2xy+y2)-2(2x2+3xy-4y2)=
3x2-2xy+y2-4x2-6xy+8y2=-x2-8xy+9y2.
(2)2A+B=2(3x2-2xy+y2)+(2x2+3xy-4y2)=
6x2-4xy+2y2+2x2+3xy-4y2=8x2-xy-2y2.
9.三个小队植树,第一队种x棵,第二队种的树比第一队种的树的2倍多8棵,第三队种的树比第二队种的树的一半少6棵,则三队共种树______棵.
10.一列火车上原有若干人,中途一半人下车,又上车(8a-5b)人,此时车上共有乘客(10a-6b)人,问车上原有乘客多少人?当a=100,b=10时,原有的乘客是多少人?
解:在中途一半人下车后且没有人上车之前时车上的人数为(10a-6b)-(8a-5b)=10a-6b-8a+5b=2a-b,则车上原有乘客2(2a-b)=(4a-2b)人.当a=100,b=10时,原有乘客4a-2b=4×100-2×10=400-20=380(人).
(4x+6)
11.三角形的周长为48,第一条边长为4a+3b,第二条边比第一条边的2倍少2a-b,求第三条边的长.
解:第三条边的长为48-(4a+3b)-[2(4a+3b)-(2a-b)]=48-4a-3b-(8a+6b-2a+b)=48-4a-3b-6a-7b=48-10a-10b.
12.已知a+2b=5,则3(2a-3b)-4(a-3b+1)+b的值为(
)
A.14
B.10
C.6
D.不能确定
13.已知M=4x2-3x-2,N=6x2-3x+6,则M,N的大小关系是(
)
A.M>N
B.M=N
C.M<N
D.以上结论都不对
C
C
2
18.为了全面提高学生的能力,学校组织课外活动,并要求七年级学生积极参加.七年级共有四个班,参加的学生共有(6a-3b)人,其中一班有a人参加,二班参加的人数比一班参加的人数的两倍少b人,三班参加的人数比二班参加的人数的一半多1人.
(1)求三班参加的人数(用含a,b的式子表示);
(2)求四班参加的人数(用含a,b的式子表示);
(3)若四个班共54人参加了课外活动,求二班比三班多多少人参加?
再
见
2.2
整式的加减
人教版·
数学·
七年级(上)
第二章
整式的加减
第3课时
整式的加减
1.能熟练进行整式的加减运算。(重点)
2.能利用整式的加减解决实际问题。(难点)
学习目标
任意写一个两位数,交换它的十位数字与个位数字,又得到一个数,两个数相加,重复几次看看.这些和有什么规律?对于任意一个两位数都成立吗?
导入新知
交换这个两位数的十位数字和个位数字,得到的数是
.
(10a+b)+(10b+a)=10a+b+10b+a=11a+11b=11(a+b)
10b+a
结论:这些和都是11的倍数.
如果用a,b分别表示一个两位数的十位数字和个位数字,那么这个两位数可以表示为
.
10a+b
.
将这两个数相加,得
P67例6
计算:
(1)
(2x-3y)+(5x+4y)
;
(2)
(8a-7b)-(4a-5b).
分析:第(1)题是计算多项式2x
-3y和5x+4y的和;
第(2)题是计算多项式8a-7b和4a-5b的差.
解:(1)原式=
2x-3y
+5x+4y
=
7x+y.
(2)
原式=
8a-7b-4a+5b
=4a-2b.
新知一
整式的加减
合作探究
整式加减的运算法则:
一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项.
注意:(1)
整式加减的结果要最简:①不能有同类项;②含字母项的系数不能出现带分数,带分数要化成假分数;③一般不含括号.
(2)
整式加减的结果如果是多项式,一般按照某一字母的升幂或降幂排列.
P69例9
求2(x-y2)+(-
x+
y2)的值,其中x=-2,y=
解-2(x-y2)+(-
x+
y2)
=-2x+
y2
-
+
y2
=-3x+
y2.
当x=-2,y=
时,原式=3×(-2)+()2=6+
=6
.
整式的化简求值以整式的加减运算为基础,具体步骤如下:
一化:利用整式加减的运算法则将整式化简;
二代:把已知字母或某个整式的值代入化简后的式子;
三计算:依据有理数的运算法则进行计算.
计算:
(1)
-3(x+2y-1)-
(4x-6y);
(2)
5a2-[a2+(5a2-2a)].
解:(1)
-3(x+2y-1)-
(4x-6y)
=-3x-6y+3-2x+3y
=-5x-3y+3.
(2)
5a2-[a2+(5a2-2a)]
=5a2-(a2+5a2-2a)
=5a2-(6a2-2a)
=5a2-6a2+2a
=-a2+2a.
巩固新知
P68例7
笔记本的单价是x元,圆珠笔的单价是y元.小红买3本笔记本,2
支圆珠笔;小明买4本笔记本,3支圆珠笔.买这些笔记本和圆珠笔,小红和小明一共花费多少钱?
解:方法1
小红买笔记本和圆珠笔共花费(3x+2y)元,
小明买笔记本和圆珠笔共花费(4x+3y)元.
小红和小明一共花费(单位:元)
(3x+2y)
+(4x+3y)=3x+2y+4x+3y
=
7x+5y.
新知二
利用整式的加减解决实际问题
合作探究
方法2
小红和小明买笔记本共花费(3x+4x)元,
圆珠笔共花费(2y+3y)元.
小红和小明一共花费(单位:元)
(3x+4x)
+
(2y+3y)
=
7x+5y.
P68例7
笔记本的单价是x元,圆珠笔的单价是y元.小红买3本笔记本,2
支圆珠笔;小明买4本笔记本,3支圆珠笔.买这些笔记本和圆珠笔,小红和小明一共花费多少钱?
P68例8
做两个长方体纸盒,尺寸如下(单位:cm):
长
宽
高
小纸盒
a
b
c
大纸盒
1.5a
2b
2c
解:小纸盒的表面积是(2ab+2bc+2ac)cm2,
大纸盒的表面积是(6ab+8bc+6ac)
cm2.
(1)
做这两个纸盒共用料多少平方厘米?
(2)
做大纸盒比做小纸盒多用料多少平方厘米?
P68例8
做两个长方体纸盒,尺寸如下(单位:cm):
长
宽
高
小纸盒
a
b
c
大纸盒
1.5a
2b
2c
(1)
做这两个纸盒共用料多少平方厘米?
(2)
做大纸盒比做小纸盒多用料多少平方厘米?
(1)做这两个纸盒共用料(单位:cm2)
(2ab+2bc+2ac)+(6ab+8bc+6ac)
=8ab
+10bc+8ac.
(2)做大纸盒比做小纸盒多用料(单位:cm2)
(6ab+8bc+6ac)-(2ab+2bc+2ac)=4ab+6bc+4ac.
例8
做两个长方体纸盒,尺寸如下(单位:cm):
长
宽
高
小纸盒
a
b
c
大纸盒
1.5a
2b
2c
(1)
做这两个纸盒共用料多少平方厘米?
(2)
做大纸盒比做小纸盒多用料多少平方厘米?
1.一列火车上原有乘客(6a-2b)人,中途有一半乘客下车,又有若干乘客上车,此时车上共有乘客(10a-6b)人.试问:
中途上车的乘客有多少人?
当a=200,b=100时,中途上车的乘客有多少人?
有关整式加减的实际问题,应先根据题目中的数量关系,正确列出关系式,再按照整式加减的运算法则计算出最后结果
巩固新知
解:(1)根据题意,得
(10a-6b)-
(6a-2b)
=7a-5b.
故中途上车的乘客有(7a-5b)人.
(2)当a=200,b=100时,
7a-5b=7×200-5×100=1
400-500=900.
故中途上车的乘客有900人.
20
2.观察下图:
它们是按一定规律排列的,依照此规律,第9个图中共有
颗★.
列表:
1
2
3
4
…
9
n
4
6
8
10
…
20
2n+2
1.已知多项式2x2-x3+x与另一个多项式的和是x3+3x2-2x,求另一个多项式.
解:由题意,得x3+3x2
-2x-(2x2
–x3+x)
=x3+3x2-2x-2x2+x3-x
=2x3+x2-3x.
所以另一个多项式为2x3+x2-3x.
课堂练习
2.已知A=x2-2xy,B=y2+3xy,求2A-3B的值.
解:2A-3B=2(x2-2xy)-3(y2+3xy)
=2x2-4xy-3y2-9xy
=2x2-13xy-
3y2.
易错警示:A,B表示的多项式分别是一个整体,代入2A-3B时需要加括号.
3.先化简,再求值:a+2(2a-b)-3(a-b),其中a=-3,b=2.
解:a+2(2a-b)-3(a-b)
=a+4a-3b-3a+3b
=2a.
当a=-3时,原式=2×(-3)=-6.
将数值带入化简后的式子时,若数值是负数,要加上括号
整式化简求值的方法
一化:利用整式加减的运算法则将整式化简;
二代:把已知字母或某个整式的值代入化简后的式子;
三计算:依据有理数的运算法则进行计算.
归纳新知
D
C
课后练习
3.当x=2时,(x2-x)-2(x2-x-1)的值为(
)
A.-4
B.0
C.1
D.4
4.已知A=a2+b2-c2,B=-4a2+2b2+3c2,
若A+B+C=0,则多项式C为(
)
A.5a2+3b2+2c2
B.5a2-3b2+4c2
C.3a2-3b2-2c2
D.3a2+3b2+4c2
B
C
5.比x2+4x+3少5x2-2x+7的多项式是_______________.
6.一个式子减去-2x得-2x2-2x+1,则这个式子为___________.
-4x2+6x-4
-2x2-4x+1
7.计算:
(1)(9x-6y)-(5x-4y);
解:原式=9x-6y-5x+4y=4x-2y.
(2)(x2-y2)-3(x2-2y2);
解:原式=x2-y2-3x2+6y2=-2x2+5y2.
(3)(9a-2b)-[8a-(5b-2a)]+2c.
解:原式=9a-2b-(8a-5b+2a)+2c=
9a-2b-8a+5b-2a+2c=-a+3b+2c.
8.已知A=3x2-2xy+y2,B=2x2+3xy-4y2,求:
(1)A-2B;
(2)2A+B.
解:(1)A-2B=(3x2-2xy+y2)-2(2x2+3xy-4y2)=
3x2-2xy+y2-4x2-6xy+8y2=-x2-8xy+9y2.
(2)2A+B=2(3x2-2xy+y2)+(2x2+3xy-4y2)=
6x2-4xy+2y2+2x2+3xy-4y2=8x2-xy-2y2.
9.三个小队植树,第一队种x棵,第二队种的树比第一队种的树的2倍多8棵,第三队种的树比第二队种的树的一半少6棵,则三队共种树______棵.
10.一列火车上原有若干人,中途一半人下车,又上车(8a-5b)人,此时车上共有乘客(10a-6b)人,问车上原有乘客多少人?当a=100,b=10时,原有的乘客是多少人?
解:在中途一半人下车后且没有人上车之前时车上的人数为(10a-6b)-(8a-5b)=10a-6b-8a+5b=2a-b,则车上原有乘客2(2a-b)=(4a-2b)人.当a=100,b=10时,原有乘客4a-2b=4×100-2×10=400-20=380(人).
(4x+6)
11.三角形的周长为48,第一条边长为4a+3b,第二条边比第一条边的2倍少2a-b,求第三条边的长.
解:第三条边的长为48-(4a+3b)-[2(4a+3b)-(2a-b)]=48-4a-3b-(8a+6b-2a+b)=48-4a-3b-6a-7b=48-10a-10b.
12.已知a+2b=5,则3(2a-3b)-4(a-3b+1)+b的值为(
)
A.14
B.10
C.6
D.不能确定
13.已知M=4x2-3x-2,N=6x2-3x+6,则M,N的大小关系是(
)
A.M>N
B.M=N
C.M<N
D.以上结论都不对
C
C
2
18.为了全面提高学生的能力,学校组织课外活动,并要求七年级学生积极参加.七年级共有四个班,参加的学生共有(6a-3b)人,其中一班有a人参加,二班参加的人数比一班参加的人数的两倍少b人,三班参加的人数比二班参加的人数的一半多1人.
(1)求三班参加的人数(用含a,b的式子表示);
(2)求四班参加的人数(用含a,b的式子表示);
(3)若四个班共54人参加了课外活动,求二班比三班多多少人参加?
再
见
同课章节目录
