2021-2022学年北师大版九年级数学上册2.5一元二次方程根与系数的关系课件(第一课时,共17张PPT)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学上册2.5一元二次方程根与系数的关系课件(第一课时,共17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-30 00:03:20 | ||
图片预览


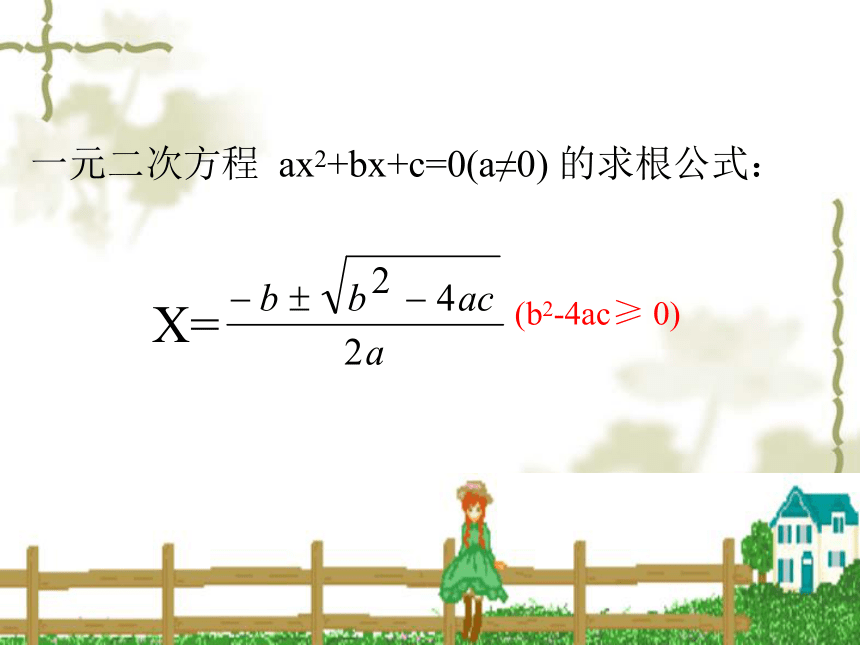




文档简介
(共17张PPT)
2.5:一元二次方程
根与系数的关系
1.一元二次方程的解法
2.求根公式
复习提问
数
学
活
动
一
一元二次方程
ax2+bx+c=0(a≠0)
的求根公式:
X=
(b2-4ac≥
0)
2
2
)
2
5
(
)
4
)(
1
(
x
x
-
=
-
(2)
(x+3)(x-1)=5
3
)
1
3
(
2
)
2
3
(
3
3
).
3
(
2
-
=
-
-
+
x
x
x
x
x
解下列方程
1.????
填表,观察、猜想
数学活动二
方程
x1,,
x2
x1,+
x2
x1.
x2
x2-2x+1=0
x2+3x-10=0
x2+5x
+4=0
问题:你发现什么规律?
①用语言叙述你发现的规律;
②
x2+px+q=0的两根x1,,
x2用式子表示你发现的规律。
根与系数关系
如果关于x的方程
的两根是
,
,则:
如果方程二次项系数不为1呢?
数
学
活
动
三
方
程
x1,,
x2
x1,+
x2
x1.
x2
2x2-3x-2=0
3x2-4x+1=0
问题:上面发现的结论在这里成立吗?请完善规律;
①用语言叙述发现的规律;
②
ax2+bx+c=0的两根x1,,
x2用式子表示你发现的规
律:
一元二次方程的根与系数的关系:
如果方程ax2+bx+c=0(a≠0)的两个根是X1
,
X2
,
那么X1+x2=
,
X1x2=
-
(韦达定理)
注:能用根与系数的关系的前提条件为b2-4ac≥0
韦达(1540-1603)
韦达是法国十六世纪最有影响的数学家之一。第一个引进系统的代数符号,并对方程论做了改进。
他生于法国的普瓦图。年青时学习法律当过律师,后从事政治活动,当过议会的议员,在对西班牙的战争中曾为政府破译敌军的密码。韦达还致力于数学研究,第一个有意识地和系统地使用字母来表示已知数、未知数及其乘幂,带来了代数学理论研究的重大进步。韦达讨论了方程根的各种有理变换,发现了方程根与系数之间的关系(所以人们把叙述一元二次方程根与系数关系的结论称为“韦达定理”)。
韦达在欧洲被尊称为“代数学之父”。
一元二次方程根与系数关系的证明:
X1+x2=
+
=
=
-
X1x2=
●
=
=
=
1、
x2
-
2x
-
1=0
2、
2x2
+
=3x
3、
2x2
-
6x
=0
4、
3x2
=
4
x1+x2=2
x1x2=-1
x1+x2=
x1+x2=3
x1+x2=0
x1x2=
x1x2=0
x1x2=
-
求下列方程的两根之和与两根之积
注:要求方程的两根之和与两根之积,方程必须要化成一般形式
例1、已知方程x2-(k+1)x+3k=0的一个根是2
,求它的另一个根及k的值。
例2、已知3x2+2x-9=0的两根是x1
,
x2
。
求:
(1)
(2)
x12+x22
变式
练习:
设x1,x2是方程2x2+4x-
3=0的两个根,利用根与系数的关系,求下列各式的值。
(2)
(1)
(3)(x1-
x2)2
1、已知方程3x2-19x+m=0的一个根是1,求它的另一个根及m的值。
2、设x1,x2是方程2x2+4x-3=0的两个根,求(x1+1)(x2+1)的值。
3、当k为何值时,方程2x2-(k+1)x+k+3=0的两根差为1。
4、设x1,x2是方程x2-2(k-1)x+k2=0的两个实数根,且x12+x22=4,求k的值。
归纳小结:
通过本节课的学习你学到了那些知识?
一元二次方程根与系数的关系(韦达定理):
两根的和等于一次项系数与二次项系数的比的相反数,两根的积等于常数项于二次项系数的比。
作业:
课本P51
习题2.8
2.5:一元二次方程
根与系数的关系
1.一元二次方程的解法
2.求根公式
复习提问
数
学
活
动
一
一元二次方程
ax2+bx+c=0(a≠0)
的求根公式:
X=
(b2-4ac≥
0)
2
2
)
2
5
(
)
4
)(
1
(
x
x
-
=
-
(2)
(x+3)(x-1)=5
3
)
1
3
(
2
)
2
3
(
3
3
).
3
(
2
-
=
-
-
+
x
x
x
x
x
解下列方程
1.????
填表,观察、猜想
数学活动二
方程
x1,,
x2
x1,+
x2
x1.
x2
x2-2x+1=0
x2+3x-10=0
x2+5x
+4=0
问题:你发现什么规律?
①用语言叙述你发现的规律;
②
x2+px+q=0的两根x1,,
x2用式子表示你发现的规律。
根与系数关系
如果关于x的方程
的两根是
,
,则:
如果方程二次项系数不为1呢?
数
学
活
动
三
方
程
x1,,
x2
x1,+
x2
x1.
x2
2x2-3x-2=0
3x2-4x+1=0
问题:上面发现的结论在这里成立吗?请完善规律;
①用语言叙述发现的规律;
②
ax2+bx+c=0的两根x1,,
x2用式子表示你发现的规
律:
一元二次方程的根与系数的关系:
如果方程ax2+bx+c=0(a≠0)的两个根是X1
,
X2
,
那么X1+x2=
,
X1x2=
-
(韦达定理)
注:能用根与系数的关系的前提条件为b2-4ac≥0
韦达(1540-1603)
韦达是法国十六世纪最有影响的数学家之一。第一个引进系统的代数符号,并对方程论做了改进。
他生于法国的普瓦图。年青时学习法律当过律师,后从事政治活动,当过议会的议员,在对西班牙的战争中曾为政府破译敌军的密码。韦达还致力于数学研究,第一个有意识地和系统地使用字母来表示已知数、未知数及其乘幂,带来了代数学理论研究的重大进步。韦达讨论了方程根的各种有理变换,发现了方程根与系数之间的关系(所以人们把叙述一元二次方程根与系数关系的结论称为“韦达定理”)。
韦达在欧洲被尊称为“代数学之父”。
一元二次方程根与系数关系的证明:
X1+x2=
+
=
=
-
X1x2=
●
=
=
=
1、
x2
-
2x
-
1=0
2、
2x2
+
=3x
3、
2x2
-
6x
=0
4、
3x2
=
4
x1+x2=2
x1x2=-1
x1+x2=
x1+x2=3
x1+x2=0
x1x2=
x1x2=0
x1x2=
-
求下列方程的两根之和与两根之积
注:要求方程的两根之和与两根之积,方程必须要化成一般形式
例1、已知方程x2-(k+1)x+3k=0的一个根是2
,求它的另一个根及k的值。
例2、已知3x2+2x-9=0的两根是x1
,
x2
。
求:
(1)
(2)
x12+x22
变式
练习:
设x1,x2是方程2x2+4x-
3=0的两个根,利用根与系数的关系,求下列各式的值。
(2)
(1)
(3)(x1-
x2)2
1、已知方程3x2-19x+m=0的一个根是1,求它的另一个根及m的值。
2、设x1,x2是方程2x2+4x-3=0的两个根,求(x1+1)(x2+1)的值。
3、当k为何值时,方程2x2-(k+1)x+k+3=0的两根差为1。
4、设x1,x2是方程x2-2(k-1)x+k2=0的两个实数根,且x12+x22=4,求k的值。
归纳小结:
通过本节课的学习你学到了那些知识?
一元二次方程根与系数的关系(韦达定理):
两根的和等于一次项系数与二次项系数的比的相反数,两根的积等于常数项于二次项系数的比。
作业:
课本P51
习题2.8
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
