2021-2022学年北师大版九年级数学上册4.4 探索三角形相似的条件课件(第三课时,共18张PPT)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学上册4.4 探索三角形相似的条件课件(第三课时,共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 878.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-30 00:00:00 | ||
图片预览



文档简介
(共18张PPT)
4.3:探索三角形相似的条件
(第三课时)
三角形相似判定方法
2.两角对应相等的两个三角形相似。
1.相似三角形的定义
复习回顾:
3.两边对应成比例且夹角相等的两个三形相似。
4.平行于三角形一边,与另外两边(或两边处长线)相交,所截得的三角形与原三角形相似。
A
B
C
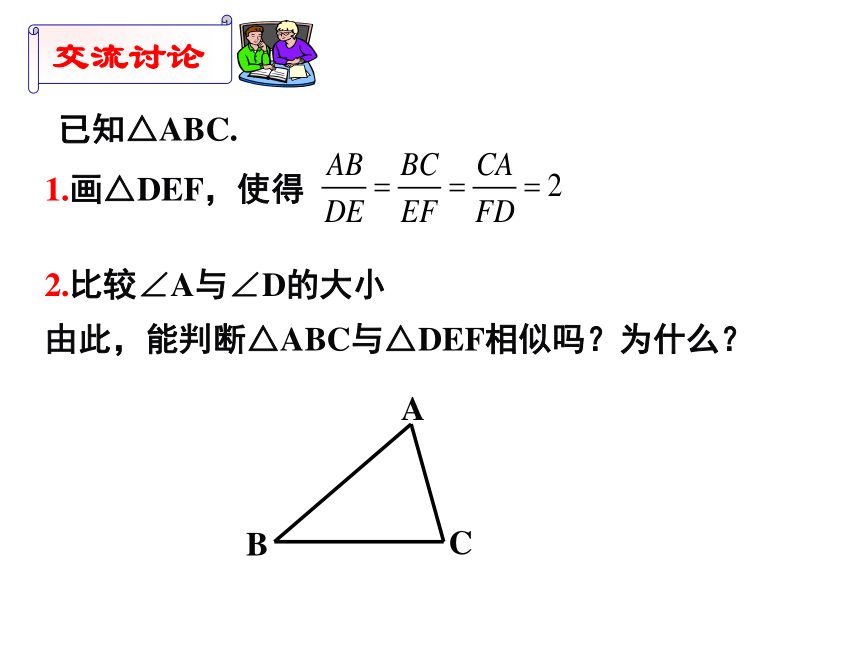
交流讨论
已知△ABC.
1.画△DEF,使得
2.比较∠A与∠D的大小
由此,能判断△ABC与△DEF相似吗?为什么?
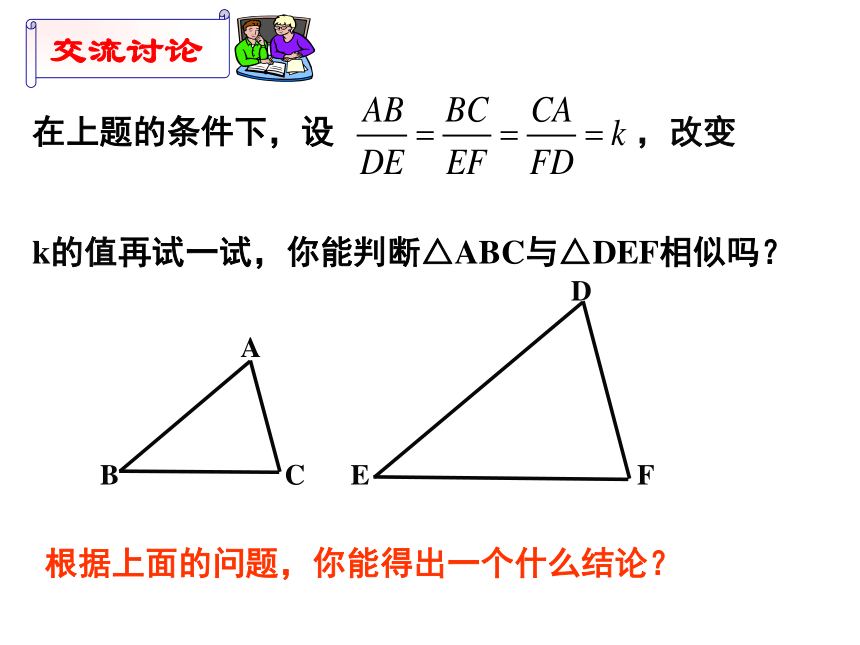
交流讨论
在上题的条件下,设
,改变
k的值再试一试,你能判断△ABC与△DEF相似吗?
A
B
C
D
E
F
根据上面的问题,你能得出一个什么结论?
A
B
C
D
E
F
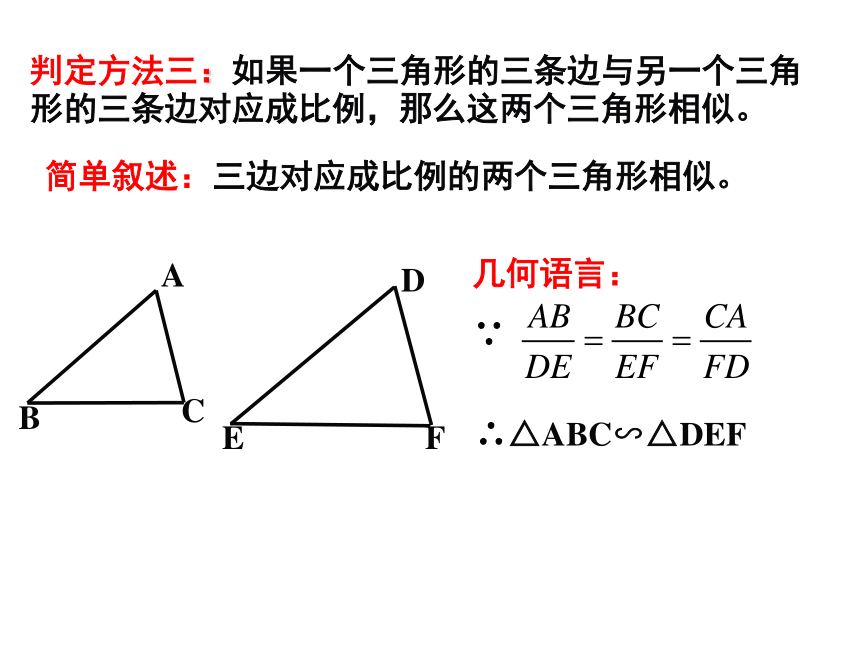
判定方法三:如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似。
几何语言:
∵
∴△ABC∽△DEF
简单叙述:三边对应成比例的两个三角形相似。
例3:如图3-16,在△ABC
和△ADE
中
,
,
∠
BAD
=
20°,求
∠
CAE
的度数.
AE
AC
DE
BC
AD
AB
=
=
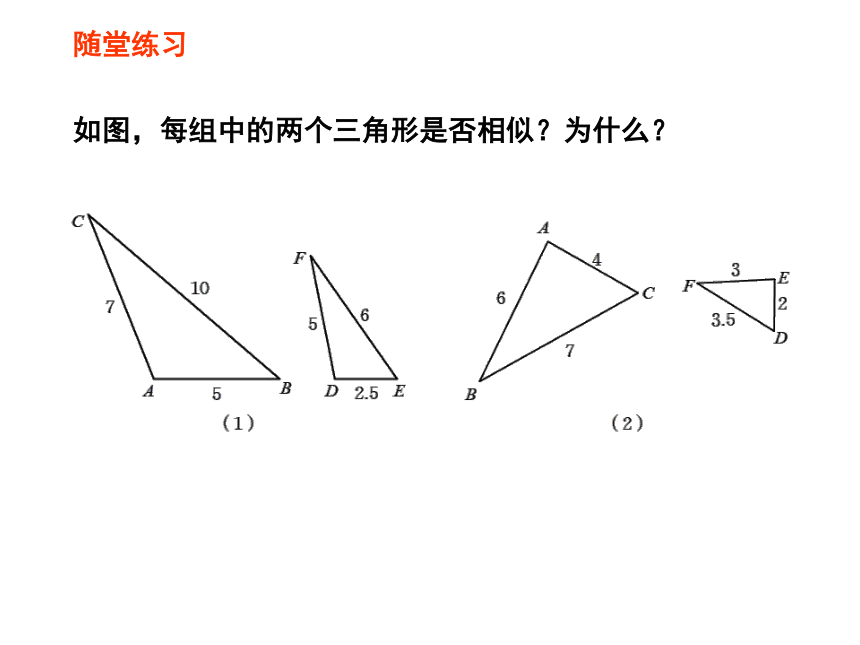
如图,每组中的两个三角形是否相似?为什么?
随堂练习
1.一个三角形三边的长分别为
6
cm,9
cm,7.5
cm,另一个三角形三边的长分别为
8
cm,10
cm,12
cm,这两个三角形相似吗?为什么?
2.如图,△ABC
与△EFG
相似吗?为什么?
知识技能
知识技能
3.如图所示的
6
个三角形中,哪些三角形相似?为什么?
已知△ABC和
△A’B’C’,根据下列条件判断它们是否相似.
(1)∠B=∠B’=75°,∠C=50°,∠A’=55°
(2)
∠A=45°,AB=12cm,
AC=15cm
∠A’=45°,A’B’=16cm,A’C’=20cm
(3)
AB=12cm,
BC=15cm,
AC=24cm
A’B’=16cm,B’C’=20cm,A’C’=30cm
已知:如图
,
试说明:∠BAD=∠BCE
A
B
C
D
E
已知△ABC的三边长分为
,
,2,△A′B′C′的两边长分别是1和
,如果△ABC与△A′B′C′相似,那么△A′B′C′的第三边长应该是(
)
A、
B、
C、
D、
如图,小正方形的边长均为1,则下图中的三角形(阴影部分)与△ABC相似的为(
)
A
C
B
B
A
C
D
要做两个形状完全相同的三角形框架,其中一个框架的三边长分别为3、4、5,另一个框架的一边长为6,怎样选料可以使两个三角形相似?
如图,已知一个等腰三角形和一条线段,以这条线段为边画三角形,使之与已知等腰三角形相似.你能画出几个形状不同的三角形?
如图,在边长为4a的正方形ABCD中,BE=3CE,CF=DF.
(1)试说明:AE2=AF2+EF2
(2)试说明:
△AEF
∽
△ADF
A
B
F
D
C
E
4.3:探索三角形相似的条件
(第三课时)
三角形相似判定方法
2.两角对应相等的两个三角形相似。
1.相似三角形的定义
复习回顾:
3.两边对应成比例且夹角相等的两个三形相似。
4.平行于三角形一边,与另外两边(或两边处长线)相交,所截得的三角形与原三角形相似。
A
B
C
交流讨论
已知△ABC.
1.画△DEF,使得
2.比较∠A与∠D的大小
由此,能判断△ABC与△DEF相似吗?为什么?
交流讨论
在上题的条件下,设
,改变
k的值再试一试,你能判断△ABC与△DEF相似吗?
A
B
C
D
E
F
根据上面的问题,你能得出一个什么结论?
A
B
C
D
E
F
判定方法三:如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似。
几何语言:
∵
∴△ABC∽△DEF
简单叙述:三边对应成比例的两个三角形相似。
例3:如图3-16,在△ABC
和△ADE
中
,
,
∠
BAD
=
20°,求
∠
CAE
的度数.
AE
AC
DE
BC
AD
AB
=
=
如图,每组中的两个三角形是否相似?为什么?
随堂练习
1.一个三角形三边的长分别为
6
cm,9
cm,7.5
cm,另一个三角形三边的长分别为
8
cm,10
cm,12
cm,这两个三角形相似吗?为什么?
2.如图,△ABC
与△EFG
相似吗?为什么?
知识技能
知识技能
3.如图所示的
6
个三角形中,哪些三角形相似?为什么?
已知△ABC和
△A’B’C’,根据下列条件判断它们是否相似.
(1)∠B=∠B’=75°,∠C=50°,∠A’=55°
(2)
∠A=45°,AB=12cm,
AC=15cm
∠A’=45°,A’B’=16cm,A’C’=20cm
(3)
AB=12cm,
BC=15cm,
AC=24cm
A’B’=16cm,B’C’=20cm,A’C’=30cm
已知:如图
,
试说明:∠BAD=∠BCE
A
B
C
D
E
已知△ABC的三边长分为
,
,2,△A′B′C′的两边长分别是1和
,如果△ABC与△A′B′C′相似,那么△A′B′C′的第三边长应该是(
)
A、
B、
C、
D、
如图,小正方形的边长均为1,则下图中的三角形(阴影部分)与△ABC相似的为(
)
A
C
B
B
A
C
D
要做两个形状完全相同的三角形框架,其中一个框架的三边长分别为3、4、5,另一个框架的一边长为6,怎样选料可以使两个三角形相似?
如图,已知一个等腰三角形和一条线段,以这条线段为边画三角形,使之与已知等腰三角形相似.你能画出几个形状不同的三角形?
如图,在边长为4a的正方形ABCD中,BE=3CE,CF=DF.
(1)试说明:AE2=AF2+EF2
(2)试说明:
△AEF
∽
△ADF
A
B
F
D
C
E
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
