2021-2022学年北师大版九年级数学上册4.6用相似三角形测量高度课件(共25张PPT)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学上册4.6用相似三角形测量高度课件(共25张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-29 23:51:35 | ||
图片预览








文档简介
(共25张PPT)
世界上最高的树
—— 红杉
世界上最宽的河
——亚马孙河
世界最高的大楼
目前世界第一高楼为哈利法塔(原名迪拜塔)。位于阿拉伯联合酋长国迪拜。总高度828米,162层。2004年9月21日开始动工,2010年1月4日竣工启用。附:2012年11月26日,长沙远大科技集团将在长沙建造一座202层,837米的世界最高楼,比现有的世界最高建筑迪拜塔,还要高。
胡夫金字塔是埃及现存规模最大的金字塔,被喻为“世界古代七大奇观之一”。塔的4个斜面正对东南西北四个方向,塔基呈正方形,每边长约230多米。据考证,为建成大金字塔,共动用了10万人花了20年时间.原高146.59米,但由于经过几千年的风吹雨打,顶端被风化吹蚀.所以高度有所降低 。
利用太阳光下的影长
利用标杆
利用镜子
A
B
C
D
E
F
方法1:利用阳光下的影子
D
F
E
A
B
C
怎么办?
A
B
C
D
E
F
A
D
F
E
B
C
∵太阳的光线是平行的
∴ AB∥DE
又B、C、 E、F在一条直线上
∴ ∠ABC= ∠DEF
∵人与旗杆是垂直于地面的
∴∠ACB= ∠DFE
∴△ABC∽△DEF
因为同学的身高AC和她的影长BC及同一时刻旗杆的影长EF均可测量得出,所以代入测量数据即可求出旗杆DF的高度
A
B
C
D
E
F
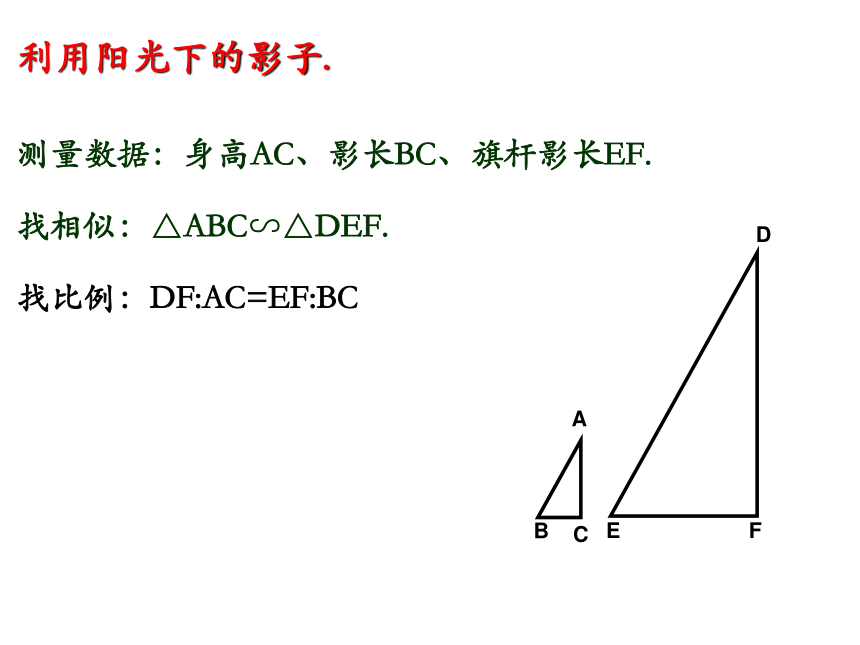
测量数据:身高AC、影长BC、旗杆影长EF.
找相似:△ABC∽△DEF.
利用阳光下的影子.
找比例:DF:AC=EF:BC
知识要点1
由相似三角形性质得:
树高 竿高
树影长 竿影长
5.4
0.9
1
1、测高的方法:测量不能到达顶部的物体的高度,通常用
什么原理解决?
在同一时刻物高与影长成比例
A
C
E
B
F
D
H
3
M
N
1
2
方法2:利用标杆
3、分别测出她的脚与旗杆底部,以及标杆底部的距离,学生眼睛到地面的高度,即可求出旗杆的高度;
操作方法:1、在观测者和旗杆之间的地面上直立一根高度已知的标杆;
2、观测者前后调整自己的位置,当旗杆顶部、标杆顶部与眼睛恰好在同一直线上时;
∴
∵人与标杆的距离AM、人与旗杆的距离AN、标杆与人眼到地面距离的差EM都可测量出
∴能求出CN
∵四边形ABND为矩形
∴DN=AB
∴能求出旗杆CD的高度CD=CN+DN
过A作AN⊥CD交EF于M
∵人、标杆和旗杆是互相平行的
∵EF∥CN
∴ ∠1= ∠2
又∠3= ∠3
∴△AME∽△ANC
A
B
C
D
E
F
M
N
测量:AB EF AM AN
构造相似:△AME∽△ANC.
找比例:
AM:AN=EM:CN
A
B
C
D
E
F
M
N
利用标杆
例 小明为测量一棵树CD的高度,他在距树24m处立了一根高为2m的标杆EF,然后小明前后调整自己的位置,当他与树相距27m时,他的眼睛、标杆的顶端和树顶端在同一直线上,已知小明身高1.6m,求树的高度。
A
N
C
E
M
F
B
D
解:过点A作AN ∥BD交CD于N、EF于M
∵人、标杆、树都垂直于地面
∴∠ABF=∠EFD =∠CDF=90
∴ AB ∥EF ∥CD
∴∠EMA=∠CNA
∵ ∠EAM=∠CAN
∴△AEM∽△CAN
∴
∵AB=1.6m,EF=2m,BD=27m,FD=24m
∴
∴ CN=3.6m,CD=3.6+1.6=5.2m
即树高为5.2m
方法3、利用镜子的反射
A
C
D
E
B
A
C
D
E
B
2
1
平面镜
操作方法:1、选一名学生作为观测者,在她与旗杆之间的地面上平放一面镜子,固定镜子的位置;
2、观测者看着镜子来回调整自己的位置,使自己能够通过镜子看到旗杆顶端,
3、测出此时她的脚与镜子的距离、旗杆底部与镜子的距离就能求出旗杆的高度。
利用镜子的反射.
测量数据:身高DE、人与镜子间的距离AE、
旗杆与镜子间距离AC.
找相似:△ADE∽△ABC.
E
C
B
D
A
找比例:AE:AC=DE:BC
议一议
上述几种测量方法各有哪些优缺点?
1.需要知道太阳角度,这个有点麻烦。如果知道了,这个方法最好了。测一个数据,结果还准确。 2.要测量的数据多了点,但结果准确。 3.镜子的角度有一点误差,结果的误差就会很大。
如图,在距离AB 18米的地面上平放着一面镜子E,人退后到距镜子2.1米的D处,在镜子里恰看见树顶,若人眼距地面1.4米,求树高。
乘胜追击
18米
1.4米
2.1米
D
B
C
E
A
∵△ABE∽△CDE
∴ =
AB B E
C D DE
分析:设树高X米
X
∴ =
X 18
1.4 2.1
X=12
即 树高为12米
如图,A、B两点分别位于一个池塘的两端,小芳想用绳子测量A、B两点之间的距离,但绳子的长度不够,一位同学帮她想了一个主意,先在地上取一个可以直接到达A、B点的点C,找到AC、BC的中点D、E,并且DE的长为5m,则A、B两点的距离是多少?
聪明才智
5米
C
B
A
E
D
解:∵△CDE∽△CAB
∴ =
5 CD
AB CA
∴ =
5 1
BE 2
∴BE=10
答:A.B两点间的距离是10米
课堂小结
在实际生活中,我们面对不能直接测量物体长度、高度和宽度时。可以建立相似三角形模型,把它们转化为数学为题,把不易测的边转化为测它的对应边的问题,再利用对应边成比例来达到求解的目的
⑵
⑷
(1)
(3)
常用的基本图形
二、 能构造并应用一些简单的相似三角形模型
拓展训练
某同学想测旗杆的高度,他在某一时刻测得1m长的竹竿竖直时的影长为1.5m,同一时刻测量旗杆影长时,因旗杆靠近一幢楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地面上的影长为9m,留在墙上的影长为2m,求旗杆的高度。
A
A'
E
D
B
C
C'
B'
C'
C
B
A
B'
A'
1.5
1
9
2
E
D
解: ∵ AB ∥A'B' BC ∥ B'C'
∴∠ABC=∠ A'B' C'
又AC⊥CB A' C'⊥B' C'
∴ ∠ACB =∠ C' =90
∴△ ABC ∽△ A'B' C'
∴
即
∴AC=6
AE=AC+CE=6+2=8
即旗杆高8米
C'
C
B
A
B'
A'
1.5
1
9
2
E
D
提示:过点D作DC∥BA交AE于C
因太阳的光线是平行的,旗杆和墙也是平行的
∴四边形ACDB为平行四边形
∴旗杆的上半部分AC与墙上的影子BD的长度是相同的
地上的影子ED是旗杆的一部分CE在地上的影子
易知△ A'B' C' ∽△CDE
∴
从而可求出CE的长
实践探索:
一油桶高0.8m,桶内有油,一根木棒长1米,从桶盖小口斜插入桶内一端到桶底,另一端到小口,抽出木棒,量得棒上浸油部分长为0.8m,则桶内油面的高度为多少米?
0.64米
A
B
C
D
E
作业:
1、书上课后习题
2、训练案
3、学海风暴
世界上最高的树
—— 红杉
世界上最宽的河
——亚马孙河
世界最高的大楼
目前世界第一高楼为哈利法塔(原名迪拜塔)。位于阿拉伯联合酋长国迪拜。总高度828米,162层。2004年9月21日开始动工,2010年1月4日竣工启用。附:2012年11月26日,长沙远大科技集团将在长沙建造一座202层,837米的世界最高楼,比现有的世界最高建筑迪拜塔,还要高。
胡夫金字塔是埃及现存规模最大的金字塔,被喻为“世界古代七大奇观之一”。塔的4个斜面正对东南西北四个方向,塔基呈正方形,每边长约230多米。据考证,为建成大金字塔,共动用了10万人花了20年时间.原高146.59米,但由于经过几千年的风吹雨打,顶端被风化吹蚀.所以高度有所降低 。
利用太阳光下的影长
利用标杆
利用镜子
A
B
C
D
E
F
方法1:利用阳光下的影子
D
F
E
A
B
C
怎么办?
A
B
C
D
E
F
A
D
F
E
B
C
∵太阳的光线是平行的
∴ AB∥DE
又B、C、 E、F在一条直线上
∴ ∠ABC= ∠DEF
∵人与旗杆是垂直于地面的
∴∠ACB= ∠DFE
∴△ABC∽△DEF
因为同学的身高AC和她的影长BC及同一时刻旗杆的影长EF均可测量得出,所以代入测量数据即可求出旗杆DF的高度
A
B
C
D
E
F
测量数据:身高AC、影长BC、旗杆影长EF.
找相似:△ABC∽△DEF.
利用阳光下的影子.
找比例:DF:AC=EF:BC
知识要点1
由相似三角形性质得:
树高 竿高
树影长 竿影长
5.4
0.9
1
1、测高的方法:测量不能到达顶部的物体的高度,通常用
什么原理解决?
在同一时刻物高与影长成比例
A
C
E
B
F
D
H
3
M
N
1
2
方法2:利用标杆
3、分别测出她的脚与旗杆底部,以及标杆底部的距离,学生眼睛到地面的高度,即可求出旗杆的高度;
操作方法:1、在观测者和旗杆之间的地面上直立一根高度已知的标杆;
2、观测者前后调整自己的位置,当旗杆顶部、标杆顶部与眼睛恰好在同一直线上时;
∴
∵人与标杆的距离AM、人与旗杆的距离AN、标杆与人眼到地面距离的差EM都可测量出
∴能求出CN
∵四边形ABND为矩形
∴DN=AB
∴能求出旗杆CD的高度CD=CN+DN
过A作AN⊥CD交EF于M
∵人、标杆和旗杆是互相平行的
∵EF∥CN
∴ ∠1= ∠2
又∠3= ∠3
∴△AME∽△ANC
A
B
C
D
E
F
M
N
测量:AB EF AM AN
构造相似:△AME∽△ANC.
找比例:
AM:AN=EM:CN
A
B
C
D
E
F
M
N
利用标杆
例 小明为测量一棵树CD的高度,他在距树24m处立了一根高为2m的标杆EF,然后小明前后调整自己的位置,当他与树相距27m时,他的眼睛、标杆的顶端和树顶端在同一直线上,已知小明身高1.6m,求树的高度。
A
N
C
E
M
F
B
D
解:过点A作AN ∥BD交CD于N、EF于M
∵人、标杆、树都垂直于地面
∴∠ABF=∠EFD =∠CDF=90
∴ AB ∥EF ∥CD
∴∠EMA=∠CNA
∵ ∠EAM=∠CAN
∴△AEM∽△CAN
∴
∵AB=1.6m,EF=2m,BD=27m,FD=24m
∴
∴ CN=3.6m,CD=3.6+1.6=5.2m
即树高为5.2m
方法3、利用镜子的反射
A
C
D
E
B
A
C
D
E
B
2
1
平面镜
操作方法:1、选一名学生作为观测者,在她与旗杆之间的地面上平放一面镜子,固定镜子的位置;
2、观测者看着镜子来回调整自己的位置,使自己能够通过镜子看到旗杆顶端,
3、测出此时她的脚与镜子的距离、旗杆底部与镜子的距离就能求出旗杆的高度。
利用镜子的反射.
测量数据:身高DE、人与镜子间的距离AE、
旗杆与镜子间距离AC.
找相似:△ADE∽△ABC.
E
C
B
D
A
找比例:AE:AC=DE:BC
议一议
上述几种测量方法各有哪些优缺点?
1.需要知道太阳角度,这个有点麻烦。如果知道了,这个方法最好了。测一个数据,结果还准确。 2.要测量的数据多了点,但结果准确。 3.镜子的角度有一点误差,结果的误差就会很大。
如图,在距离AB 18米的地面上平放着一面镜子E,人退后到距镜子2.1米的D处,在镜子里恰看见树顶,若人眼距地面1.4米,求树高。
乘胜追击
18米
1.4米
2.1米
D
B
C
E
A
∵△ABE∽△CDE
∴ =
AB B E
C D DE
分析:设树高X米
X
∴ =
X 18
1.4 2.1
X=12
即 树高为12米
如图,A、B两点分别位于一个池塘的两端,小芳想用绳子测量A、B两点之间的距离,但绳子的长度不够,一位同学帮她想了一个主意,先在地上取一个可以直接到达A、B点的点C,找到AC、BC的中点D、E,并且DE的长为5m,则A、B两点的距离是多少?
聪明才智
5米
C
B
A
E
D
解:∵△CDE∽△CAB
∴ =
5 CD
AB CA
∴ =
5 1
BE 2
∴BE=10
答:A.B两点间的距离是10米
课堂小结
在实际生活中,我们面对不能直接测量物体长度、高度和宽度时。可以建立相似三角形模型,把它们转化为数学为题,把不易测的边转化为测它的对应边的问题,再利用对应边成比例来达到求解的目的
⑵
⑷
(1)
(3)
常用的基本图形
二、 能构造并应用一些简单的相似三角形模型
拓展训练
某同学想测旗杆的高度,他在某一时刻测得1m长的竹竿竖直时的影长为1.5m,同一时刻测量旗杆影长时,因旗杆靠近一幢楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地面上的影长为9m,留在墙上的影长为2m,求旗杆的高度。
A
A'
E
D
B
C
C'
B'
C'
C
B
A
B'
A'
1.5
1
9
2
E
D
解: ∵ AB ∥A'B' BC ∥ B'C'
∴∠ABC=∠ A'B' C'
又AC⊥CB A' C'⊥B' C'
∴ ∠ACB =∠ C' =90
∴△ ABC ∽△ A'B' C'
∴
即
∴AC=6
AE=AC+CE=6+2=8
即旗杆高8米
C'
C
B
A
B'
A'
1.5
1
9
2
E
D
提示:过点D作DC∥BA交AE于C
因太阳的光线是平行的,旗杆和墙也是平行的
∴四边形ACDB为平行四边形
∴旗杆的上半部分AC与墙上的影子BD的长度是相同的
地上的影子ED是旗杆的一部分CE在地上的影子
易知△ A'B' C' ∽△CDE
∴
从而可求出CE的长
实践探索:
一油桶高0.8m,桶内有油,一根木棒长1米,从桶盖小口斜插入桶内一端到桶底,另一端到小口,抽出木棒,量得棒上浸油部分长为0.8m,则桶内油面的高度为多少米?
0.64米
A
B
C
D
E
作业:
1、书上课后习题
2、训练案
3、学海风暴
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
