2021-2022学年北师大版九年级数学上册4.7相似三角形的性质课件(共34张PPT)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学上册4.7相似三角形的性质课件(共34张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 374.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-29 23:54:06 | ||
图片预览





文档简介
(共34张PPT)
在10倍的放大镜下看到的三角形与原三角形相比,三角形的边长,周长,面积,角,会发生哪些变化?
4.7:相似三角形的性质
定义
方法一
方法二
方法三
全等
相似
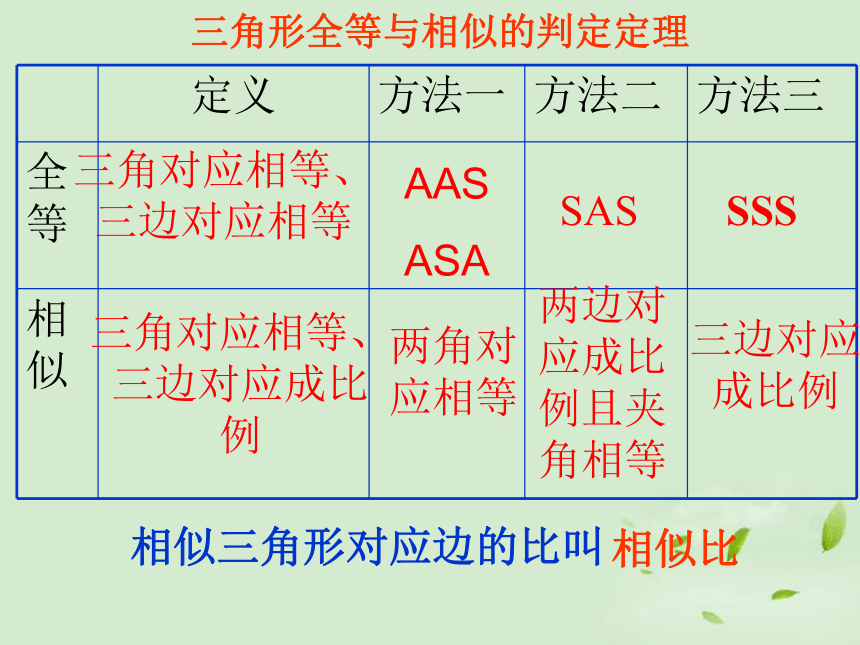
三角形全等与相似的判定定理
三角对应相等、三边对应相等
AAS
ASA
SAS
SSS
三角对应相等、三边对应成比例
两角对应相等
两边对应成比例且夹角相等
三边对应成比例
相似三角形对应边的比叫
相似比
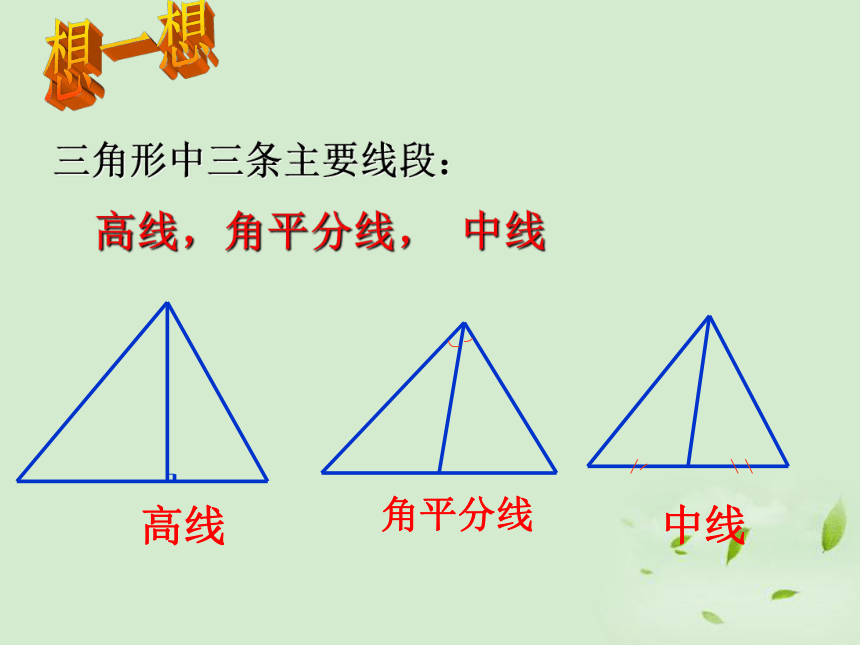
三角形中三条主要线段:
高线,角平分线,
中线
高线
角平分线
中线
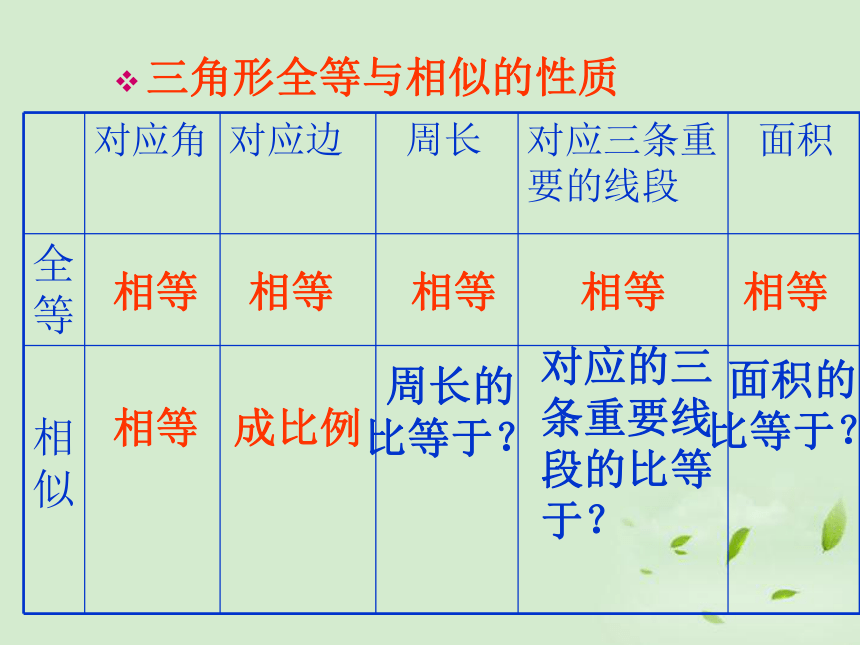
三角形全等与相似的性质
对应角
对应边
周长
对应三条重要的线段
面积
全等
相似
相等
相等
相等
相等
相等
相等
成比例
对应的三条重要线段的比等于?
面积的比等于?
周长的比等于?
阅读教材P106-110页内容
学习目标:
1.经历探索相似三角形中对应线段的比、周长的比、面积的比性质的过程。
2.能运用对应线段比、周长比、面积比性质进行有关的计算。
学习重点:
利用相似三角形周长比、面积比的性质解决计算问题。
学习难点:
相似三角形性质中周长比、面积比性质的结论的得出
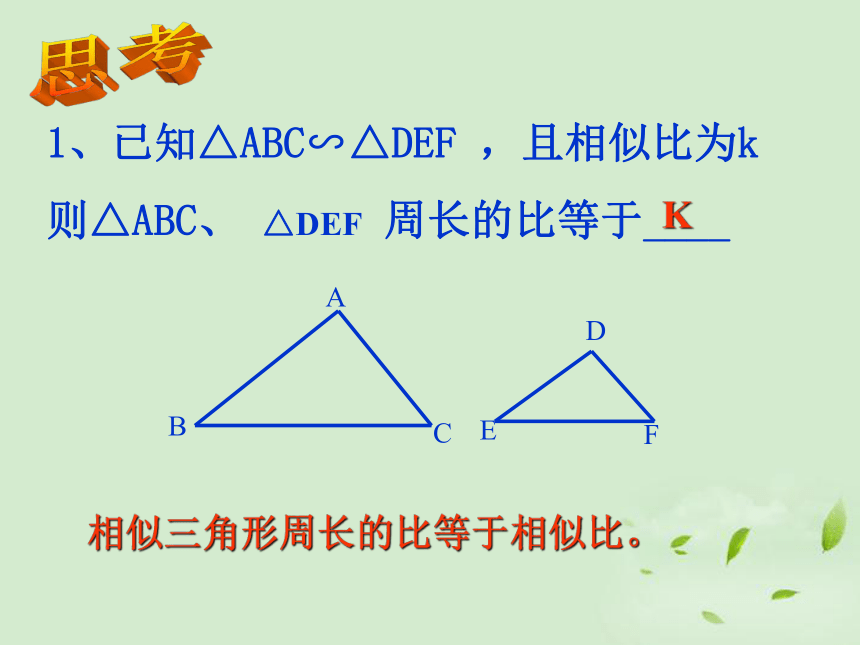
1、已知△ABC∽△DEF
,且相似比为k
则△ABC、
△DEF
周长的比等于____
相似三角形周长的比等于相似比。
K
A
B
C
D
E
F
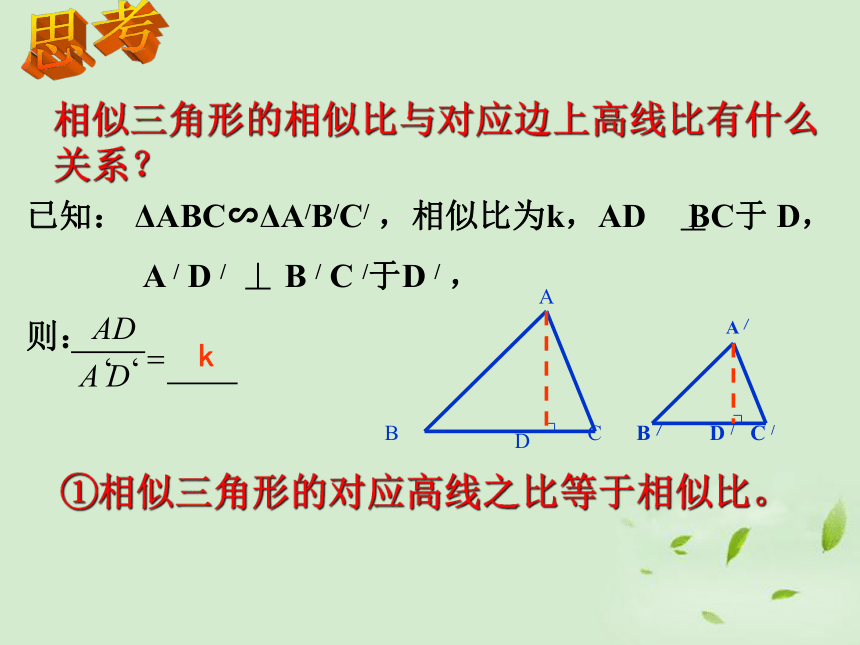
相似三角形的相似比与对应边上高线比有什么关系?
已知:
ΔABC∽ΔA/B/C/
,相似比为k,AD
BC于
D,
A
/
D
/
B
/
C
/于D
/
,
则:
A
B
C
D
A
/
B
/
C
/
D
/
①相似三角形的对应高线之比等于相似比。
k
‘
‘
AD
A
D
=
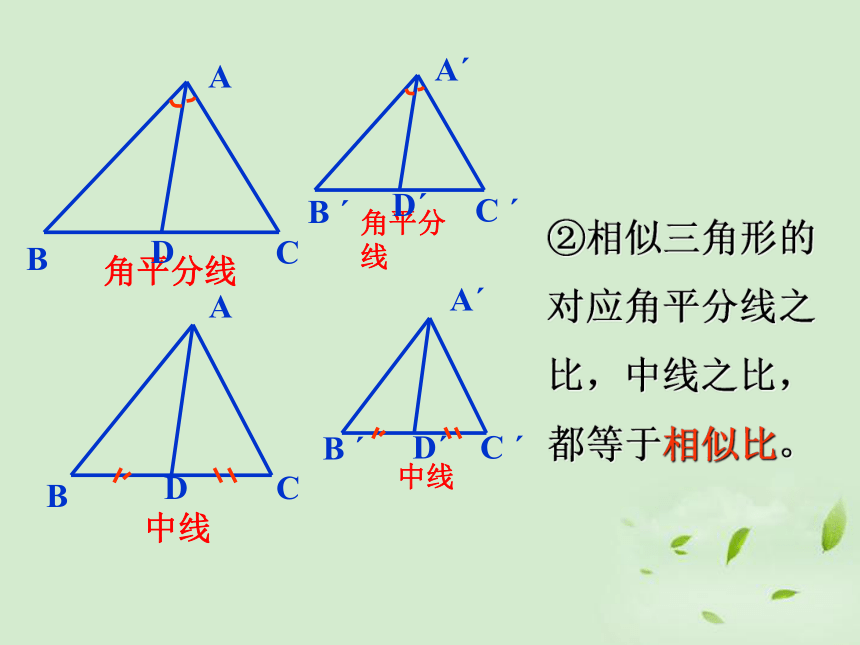
角平分线
角平分线
中线
中线
②相似三角形的
对应角平分线之
比,中线之比,
都等于相似比。
A
B
C
Aˊ
Aˊ
B
ˊ
B
ˊ
C
ˊ
C
ˊ
C
B
A
D
Dˊ
D
Dˊ
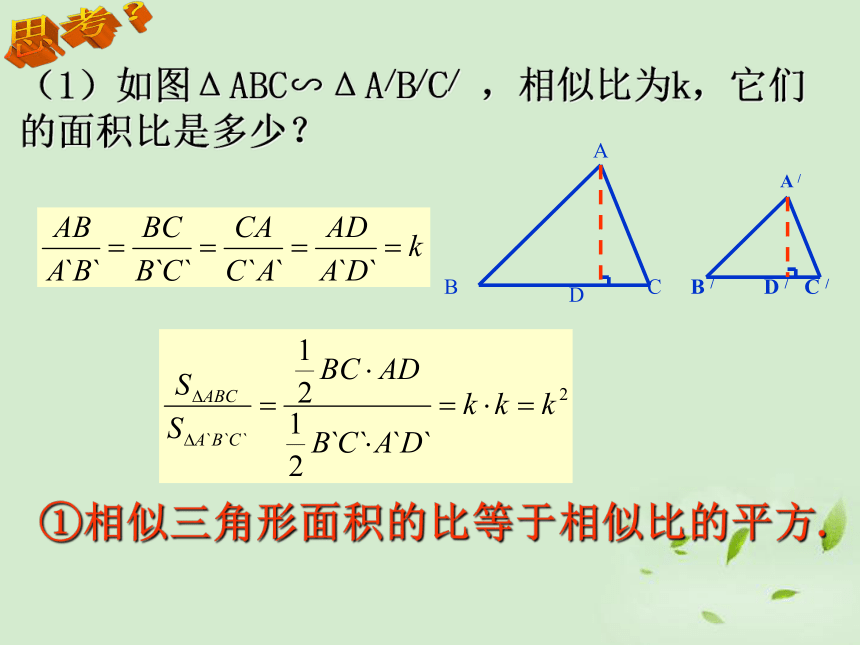
(1)如图ΔABC∽ΔA/B/C/
,相似比为k,它们的面积比是多少?
①相似三角形面积的比等于相似比的平方.
A
B
C
D
A
/
B
/
C
/
D
/
三角形全等与相似的性质
对应角
对应边
周长
对应三条重要的线段
面积
全等
相似
相等
相等
相等
相等
相等
相等
成比例
对应的三条重要线段的比等于?
面积的比等于?
周长的比等于?
相似比
相似比
相似比的平方
在10倍的放大镜下看到的三角形与原三角形相比,
三角形的边长,周长,面积,角,会发生哪些变化?
答:三角形的边长,周长放大为原来的10倍.
三角形的面积放大为原来的100倍.
三角形的角大小不变.
已知两个三角形相似,请完成下列表格
相似比
周长比
面积比
注:周长比等于相似比,已知相似比或周长比,
求面积比要平方;
而已知面积比,求相似比或
周长比则要开方。
2
4
100
100
10000
1
9
1
3
1
3
2
...
...
...
1、判断题:
(1)如果把一个三角形各边同时扩大为原来的5倍,那么它的周长也扩大为原来的5倍。
(√)
(2)如果把一个三角形的面积扩大为原来的9倍,那么它的三边也扩大为原来的9倍。
(×)
基础练习
2、如图,△ABC∽△AˊBˊCˊ
,它们的周长分别为60cm和72cm,且AB=15cm,BˊCˊ
=24cm,
求BC=_____、AC=______、
AˊBˊ=______、AˊCˊ=________。
A
B
C
B`
A`
C`
15
24
3、如图在ΔABC
和ΔDEF中,AB=2DE,AC=2DF,∠A=∠D,ΔABC的周长是24,面积是48,求ΔDEF的周长和面积。
A
B
C
D
E
F
4、如图,在△ABC中,D是AB的中点,
DE∥
BC,则:
(1)S
△ADE
:
S
△ABC
=____________
(2)S
△ADE:
S
梯形DBCE
=____________
1:4
1:3
5、如图,是一块三角形木板,工人师傅要把它切割成:一块为三角形,另一块为梯形,且要使切割出的三角形与梯形的面积之比为4:5,那么该怎么切割呢?
A
B
C
D
E
有几种切割方法?
6、如图,△ABC,DE//BC,且△ADE的面积等于梯形BCED的面积,则△ADE与△ABC的相似比是_______
B
A
D
E
C
7、如图,平行四边形ABCD中,AE:EB=1:2,则△AEF与△CDF周长的比=
。如果S△AEF=6
cm2,求S△CDF=_________
一、填空
1、已知ΔABC与ΔA/B/C/
的相似比为2:3,
则周长比为
,对应边上中线之比
,
面积之比为
。
2、已知ΔABC∽ΔA/B/C/,且面积之比为9:4,
则周长之比为
,相似比
,对应边上的
高线之比
。
2:3
4:9
3:2
3:
2
3:2
2:3
3、如图,在△ABC中,点D、E分别是AB、AC的中点。
(3)若S△DOE=1cm2,求S△OBC
,S△OEC
和S△ABC.
(1)找出图中的各对相似三角形;
(2)各对相似三角形的相似比
分别是多少?面积的比呢?
F
4.如图,S□ABCD=2080cm2,点E是平行四边形ABCD
的边AB的延长线上一点,且
,那么
S△BEF
=
.
A
B
C
D
E
F
1、如图,这是圆桌正上方的灯泡(当成一个点)发出的光线照射桌面形成阴影的示意图,已知桌面的直径为1.2米,桌面距离地面为1米,若灯泡距离地面3米,则地面上阴影部分的面积为多少?
F
E
D
C
B
A
H
2、
如图,△ABC是一块锐角三角形余料,
边BC=120毫米,高AD=80毫米,要把它加
工成正方形零件,使正方形的一边在BC上,
其余两个顶点分别在AB、AC上,这个正方
形零件的边长是多少?
N
M
Q
P
E
D
C
B
A
解:设正方形PQMN是符合要求的△ABC的高AD与PN相交于点E。设正方形PQMN的边长为x毫米。
∵PN∥BC
∴△APN∽
△ABC
∴
AE
AD
=
PN
BC
因此
,得
x=48(毫米)。答:----。
80–x
80
=
x
120
3、如图,矩形FGHN内接于△ABC,FG在BC上,NH分别在AB、AC上,且AD⊥BC于D,交NH于E,AD=8cm,BC=24cm,
(1)
△ABC∽
△ANH成立吗?试说明理由;
(2)设矩形的一边长NF=x,求矩形
FGHN
的面积y与x的关系式。
A
B
C
N
H
E
F
D
G
(3)你能求出矩形FGHN
的面积y的最大值吗?
(1)相似三角形对应的
比等于相似比.
相似三角形的性质:
(3)相似
面积的比等于相似比的平方.
(2)相似
周长的比等于相似比.
三角形
三角形
高线
角平分线
中线
在10倍的放大镜下看到的三角形与原三角形相比,三角形的边长,周长,面积,角,会发生哪些变化?
4.7:相似三角形的性质
定义
方法一
方法二
方法三
全等
相似
三角形全等与相似的判定定理
三角对应相等、三边对应相等
AAS
ASA
SAS
SSS
三角对应相等、三边对应成比例
两角对应相等
两边对应成比例且夹角相等
三边对应成比例
相似三角形对应边的比叫
相似比
三角形中三条主要线段:
高线,角平分线,
中线
高线
角平分线
中线
三角形全等与相似的性质
对应角
对应边
周长
对应三条重要的线段
面积
全等
相似
相等
相等
相等
相等
相等
相等
成比例
对应的三条重要线段的比等于?
面积的比等于?
周长的比等于?
阅读教材P106-110页内容
学习目标:
1.经历探索相似三角形中对应线段的比、周长的比、面积的比性质的过程。
2.能运用对应线段比、周长比、面积比性质进行有关的计算。
学习重点:
利用相似三角形周长比、面积比的性质解决计算问题。
学习难点:
相似三角形性质中周长比、面积比性质的结论的得出
1、已知△ABC∽△DEF
,且相似比为k
则△ABC、
△DEF
周长的比等于____
相似三角形周长的比等于相似比。
K
A
B
C
D
E
F
相似三角形的相似比与对应边上高线比有什么关系?
已知:
ΔABC∽ΔA/B/C/
,相似比为k,AD
BC于
D,
A
/
D
/
B
/
C
/于D
/
,
则:
A
B
C
D
A
/
B
/
C
/
D
/
①相似三角形的对应高线之比等于相似比。
k
‘
‘
AD
A
D
=
角平分线
角平分线
中线
中线
②相似三角形的
对应角平分线之
比,中线之比,
都等于相似比。
A
B
C
Aˊ
Aˊ
B
ˊ
B
ˊ
C
ˊ
C
ˊ
C
B
A
D
Dˊ
D
Dˊ
(1)如图ΔABC∽ΔA/B/C/
,相似比为k,它们的面积比是多少?
①相似三角形面积的比等于相似比的平方.
A
B
C
D
A
/
B
/
C
/
D
/
三角形全等与相似的性质
对应角
对应边
周长
对应三条重要的线段
面积
全等
相似
相等
相等
相等
相等
相等
相等
成比例
对应的三条重要线段的比等于?
面积的比等于?
周长的比等于?
相似比
相似比
相似比的平方
在10倍的放大镜下看到的三角形与原三角形相比,
三角形的边长,周长,面积,角,会发生哪些变化?
答:三角形的边长,周长放大为原来的10倍.
三角形的面积放大为原来的100倍.
三角形的角大小不变.
已知两个三角形相似,请完成下列表格
相似比
周长比
面积比
注:周长比等于相似比,已知相似比或周长比,
求面积比要平方;
而已知面积比,求相似比或
周长比则要开方。
2
4
100
100
10000
1
9
1
3
1
3
2
...
...
...
1、判断题:
(1)如果把一个三角形各边同时扩大为原来的5倍,那么它的周长也扩大为原来的5倍。
(√)
(2)如果把一个三角形的面积扩大为原来的9倍,那么它的三边也扩大为原来的9倍。
(×)
基础练习
2、如图,△ABC∽△AˊBˊCˊ
,它们的周长分别为60cm和72cm,且AB=15cm,BˊCˊ
=24cm,
求BC=_____、AC=______、
AˊBˊ=______、AˊCˊ=________。
A
B
C
B`
A`
C`
15
24
3、如图在ΔABC
和ΔDEF中,AB=2DE,AC=2DF,∠A=∠D,ΔABC的周长是24,面积是48,求ΔDEF的周长和面积。
A
B
C
D
E
F
4、如图,在△ABC中,D是AB的中点,
DE∥
BC,则:
(1)S
△ADE
:
S
△ABC
=____________
(2)S
△ADE:
S
梯形DBCE
=____________
1:4
1:3
5、如图,是一块三角形木板,工人师傅要把它切割成:一块为三角形,另一块为梯形,且要使切割出的三角形与梯形的面积之比为4:5,那么该怎么切割呢?
A
B
C
D
E
有几种切割方法?
6、如图,△ABC,DE//BC,且△ADE的面积等于梯形BCED的面积,则△ADE与△ABC的相似比是_______
B
A
D
E
C
7、如图,平行四边形ABCD中,AE:EB=1:2,则△AEF与△CDF周长的比=
。如果S△AEF=6
cm2,求S△CDF=_________
一、填空
1、已知ΔABC与ΔA/B/C/
的相似比为2:3,
则周长比为
,对应边上中线之比
,
面积之比为
。
2、已知ΔABC∽ΔA/B/C/,且面积之比为9:4,
则周长之比为
,相似比
,对应边上的
高线之比
。
2:3
4:9
3:2
3:
2
3:2
2:3
3、如图,在△ABC中,点D、E分别是AB、AC的中点。
(3)若S△DOE=1cm2,求S△OBC
,S△OEC
和S△ABC.
(1)找出图中的各对相似三角形;
(2)各对相似三角形的相似比
分别是多少?面积的比呢?
F
4.如图,S□ABCD=2080cm2,点E是平行四边形ABCD
的边AB的延长线上一点,且
,那么
S△BEF
=
.
A
B
C
D
E
F
1、如图,这是圆桌正上方的灯泡(当成一个点)发出的光线照射桌面形成阴影的示意图,已知桌面的直径为1.2米,桌面距离地面为1米,若灯泡距离地面3米,则地面上阴影部分的面积为多少?
F
E
D
C
B
A
H
2、
如图,△ABC是一块锐角三角形余料,
边BC=120毫米,高AD=80毫米,要把它加
工成正方形零件,使正方形的一边在BC上,
其余两个顶点分别在AB、AC上,这个正方
形零件的边长是多少?
N
M
Q
P
E
D
C
B
A
解:设正方形PQMN是符合要求的△ABC的高AD与PN相交于点E。设正方形PQMN的边长为x毫米。
∵PN∥BC
∴△APN∽
△ABC
∴
AE
AD
=
PN
BC
因此
,得
x=48(毫米)。答:----。
80–x
80
=
x
120
3、如图,矩形FGHN内接于△ABC,FG在BC上,NH分别在AB、AC上,且AD⊥BC于D,交NH于E,AD=8cm,BC=24cm,
(1)
△ABC∽
△ANH成立吗?试说明理由;
(2)设矩形的一边长NF=x,求矩形
FGHN
的面积y与x的关系式。
A
B
C
N
H
E
F
D
G
(3)你能求出矩形FGHN
的面积y的最大值吗?
(1)相似三角形对应的
比等于相似比.
相似三角形的性质:
(3)相似
面积的比等于相似比的平方.
(2)相似
周长的比等于相似比.
三角形
三角形
高线
角平分线
中线
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
