角平分线的性质与判定学案
文档属性
| 名称 | 角平分线的性质与判定学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 176.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-07-22 07:51:08 | ||
图片预览

文档简介
§11.3 角平分线的性质 两课时 学案
教学目标
1、能够证明角平分线的性质定理、判定定理
2、能够运用角平分线的性质定理、判定定理解决几何问题
教学重点和难点
重点:角平分线的性质定理、判定定理
难点:利用角平分线的性质定理、判定定理解决几何问题
教学过程设计
探究:
下图是一个平分角的仪器,其中AB=AD,BC=DC.将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是角平分线.你能说明它的道理吗?要说明AC是∠DAC的平分线,其实就是证明∠CAD=∠CAB.
思考:
1.用 可以截相等的线段
2.在以上基础上,已知一角如何画出该角的平分线
一、尺规作图
1、已知:∠AOB, 2、练习,画出下列角的平分线
求作:∠AOB的平分线OC
3、练习,教材P19
3.已知 ∠AOB,OC平分线∠AOB,你会利用此图构造全等三角形吗
二、角平分线的性质
(1)点到直线的距离:从直线外一点向直线引垂线,这点到垂足间线段的长叫做这点到直线的距离。
探究: 课本20页
如图:OP平分∠AOB ,PE⊥OA,PD⊥OB,显然PD的长度是 , PE的长度是
PE,PD有何关系? 请加以证明
证明:
角平分线性质定理( 即已知角的平分线,能推出什么样的结论)
数学语言:
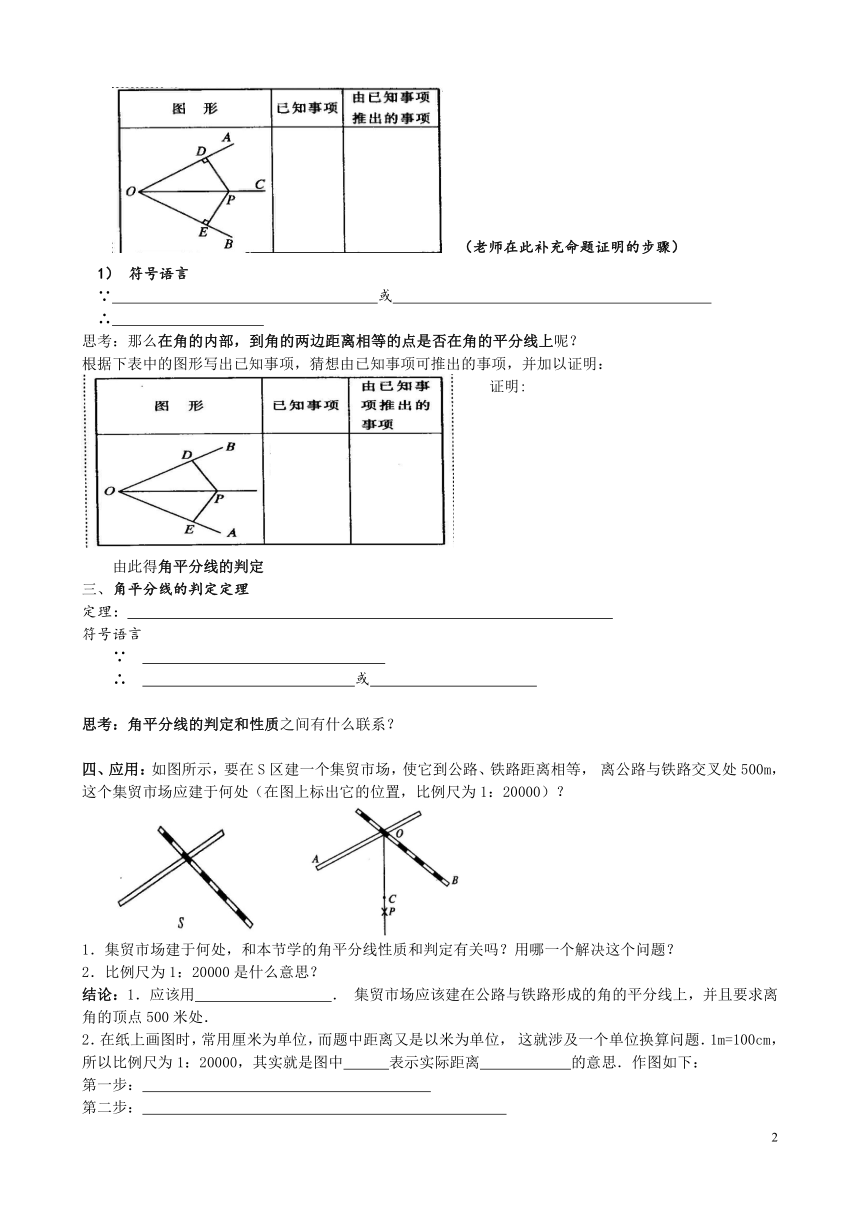
用符号语言来翻译这句话.请填下表:
(老师在此补充命题证明的步骤)
符号语言
∵ 或
∴
思考:那么在角的内部,到角的两边距离相等的点是否在角的平分线上呢?
根据下表中的图形写出已知事项,猜想由已知事项可推出的事项,并加以证明:
证明:
由此得角平分线的判定
三、角平分线的判定定理
定理:
符号语言
∵
∴ 或
思考:角平分线的判定和性质之间有什么联系?
四、应用:如图所示,要在S区建一个集贸市场,使它到公路、铁路距离相等,离公路与铁路交叉处500m,这个集贸市场应建于何处(在图上标出它的位置,比例尺为1:20000)?
1.集贸市场建于何处,和本节学的角平分线性质和判定有关吗?用哪一个解决这个问题?
2.比例尺为1:20000是什么意思?
结论:1.应该用 .集贸市场应该建在公路与铁路形成的角的平分线上,并且要求离角的顶点500米处.
2.在纸上画图时,常用厘米为单位,而题中距离又是以米为单位,这就涉及一个单位换算问题.1m=100cm,所以比例尺为1:20000,其实就是图中 表示实际距离 的意思.作图如下:
第一步:
第二步:
总结:应用角平分线的性质和判定,可以省去证明三角形全等的步骤,使问题简单化.所以若遇到有关角平分线,又要证线段相等的问题,可以直接利用性质解决问题.
五、练习
1、如图,△ABC的角平分线BM、CN相交于点P.求证:点P到三边AB、BC、CA的距离相等.
思考:点P在∠A的平分线上吗?为什么?
2、如图,△ABC的∠B的外角平分线BD与∠C的外角的平分组CE相交于P,
求证点P到三边AB,BC,CA所在直线的距离相等。
思考:到三角形三边所在直线距离相等的点有几个?
讲解例题
如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于O,且∠1 =∠2。
求证:OB = OC。
如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于O,且OB = OC。
求证:∠1 =∠2。
例3.在△ABC中,AC⊥BC,AD为∠BAC的平分线,DE⊥AB,AB=7㎝,AC=3㎝,求BE的长。
课堂练习:
1.在Rt△ABC中,BD平分∠ABC,DE⊥AB于E,则:⑴图中相等的线段有哪些?相等的角呢?⑵哪条线段与DE相等?为什么?⑶若AB=10,BC=8,AC=6,求BE,AE的长和△AED的周长
2.如图:在△ABC中,∠C=90° AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;求证:CF=EB
3.△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB,DF⊥AC,垂足分别为E,F,求证EB=FC
4.如图,在△ABC中,AC = BC,∠C = 90°,AD是△ABC的角平分线,
DE⊥AB,垂足为E。 求证:AB = AC + CD。 (选做)
课后练习:
1.如图,E是线段AC上的一点,AB⊥EB于B,AD⊥ED于D,且∠1 =∠2,CB = CD。求证:∠3 =∠4。
如图,在△ABC中,BE⊥AC,AD⊥BC,AD、BE相交于点P,AE = BD。求证:P在∠ACB的角平分线上。
如图,E为AB边上的一点,DA⊥AB于A,CB⊥AB于B,∠1 =∠C,DE = EC。求证:DA + CB = AB。
如图,AB = AC,DE为△ABC的AB边的垂直平分线,D为垂足,DE交BC于E。
求证:BE + EC = AB。
(若已补充线段的垂直平分线的性质此题可做)
C
E
D
C
B
A
A
B
C
D
E
F
A
B
C
D
E
PAGE
1
教学目标
1、能够证明角平分线的性质定理、判定定理
2、能够运用角平分线的性质定理、判定定理解决几何问题
教学重点和难点
重点:角平分线的性质定理、判定定理
难点:利用角平分线的性质定理、判定定理解决几何问题
教学过程设计
探究:
下图是一个平分角的仪器,其中AB=AD,BC=DC.将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是角平分线.你能说明它的道理吗?要说明AC是∠DAC的平分线,其实就是证明∠CAD=∠CAB.
思考:
1.用 可以截相等的线段
2.在以上基础上,已知一角如何画出该角的平分线
一、尺规作图
1、已知:∠AOB, 2、练习,画出下列角的平分线
求作:∠AOB的平分线OC
3、练习,教材P19
3.已知 ∠AOB,OC平分线∠AOB,你会利用此图构造全等三角形吗
二、角平分线的性质
(1)点到直线的距离:从直线外一点向直线引垂线,这点到垂足间线段的长叫做这点到直线的距离。
探究: 课本20页
如图:OP平分∠AOB ,PE⊥OA,PD⊥OB,显然PD的长度是 , PE的长度是
PE,PD有何关系? 请加以证明
证明:
角平分线性质定理( 即已知角的平分线,能推出什么样的结论)
数学语言:
用符号语言来翻译这句话.请填下表:
(老师在此补充命题证明的步骤)
符号语言
∵ 或
∴
思考:那么在角的内部,到角的两边距离相等的点是否在角的平分线上呢?
根据下表中的图形写出已知事项,猜想由已知事项可推出的事项,并加以证明:
证明:
由此得角平分线的判定
三、角平分线的判定定理
定理:
符号语言
∵
∴ 或
思考:角平分线的判定和性质之间有什么联系?
四、应用:如图所示,要在S区建一个集贸市场,使它到公路、铁路距离相等,离公路与铁路交叉处500m,这个集贸市场应建于何处(在图上标出它的位置,比例尺为1:20000)?
1.集贸市场建于何处,和本节学的角平分线性质和判定有关吗?用哪一个解决这个问题?
2.比例尺为1:20000是什么意思?
结论:1.应该用 .集贸市场应该建在公路与铁路形成的角的平分线上,并且要求离角的顶点500米处.
2.在纸上画图时,常用厘米为单位,而题中距离又是以米为单位,这就涉及一个单位换算问题.1m=100cm,所以比例尺为1:20000,其实就是图中 表示实际距离 的意思.作图如下:
第一步:
第二步:
总结:应用角平分线的性质和判定,可以省去证明三角形全等的步骤,使问题简单化.所以若遇到有关角平分线,又要证线段相等的问题,可以直接利用性质解决问题.
五、练习
1、如图,△ABC的角平分线BM、CN相交于点P.求证:点P到三边AB、BC、CA的距离相等.
思考:点P在∠A的平分线上吗?为什么?
2、如图,△ABC的∠B的外角平分线BD与∠C的外角的平分组CE相交于P,
求证点P到三边AB,BC,CA所在直线的距离相等。
思考:到三角形三边所在直线距离相等的点有几个?
讲解例题
如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于O,且∠1 =∠2。
求证:OB = OC。
如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于O,且OB = OC。
求证:∠1 =∠2。
例3.在△ABC中,AC⊥BC,AD为∠BAC的平分线,DE⊥AB,AB=7㎝,AC=3㎝,求BE的长。
课堂练习:
1.在Rt△ABC中,BD平分∠ABC,DE⊥AB于E,则:⑴图中相等的线段有哪些?相等的角呢?⑵哪条线段与DE相等?为什么?⑶若AB=10,BC=8,AC=6,求BE,AE的长和△AED的周长
2.如图:在△ABC中,∠C=90° AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;求证:CF=EB
3.△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB,DF⊥AC,垂足分别为E,F,求证EB=FC
4.如图,在△ABC中,AC = BC,∠C = 90°,AD是△ABC的角平分线,
DE⊥AB,垂足为E。 求证:AB = AC + CD。 (选做)
课后练习:
1.如图,E是线段AC上的一点,AB⊥EB于B,AD⊥ED于D,且∠1 =∠2,CB = CD。求证:∠3 =∠4。
如图,在△ABC中,BE⊥AC,AD⊥BC,AD、BE相交于点P,AE = BD。求证:P在∠ACB的角平分线上。
如图,E为AB边上的一点,DA⊥AB于A,CB⊥AB于B,∠1 =∠C,DE = EC。求证:DA + CB = AB。
如图,AB = AC,DE为△ABC的AB边的垂直平分线,D为垂足,DE交BC于E。
求证:BE + EC = AB。
(若已补充线段的垂直平分线的性质此题可做)
C
E
D
C
B
A
A
B
C
D
E
F
A
B
C
D
E
PAGE
1
