华师大版数学八上12.3.1平方差公式课件(19张ppt)
文档属性
| 名称 | 华师大版数学八上12.3.1平方差公式课件(19张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 948.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-30 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
?
?
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
计算下列各题:
(a+2)(a-2)=________________
(3-x)(3+x)=________________
(a+b)(a-b
)=________________
(4)
(2m+n)(2m-n)=_______________
比较等号两边的代数式,它们在系数和字母方面各有什么特点?两者有什么联系?
知识复习:
多项式与多项式相乘的法则:
(a+n)(b+m)=
ab
+nb
+am
+nm
观察
&
发现
?
观察以上算式及其运算结果,你发现了什么规律?
用自己的语言叙述你的发现.
两数和与这两数差的积,等于这两数的平方的差.
平方差公式:
即两数和与这两数差的积等于这两个数的平方差.
公式中的a,b可以是数,还可以是单项式或多项式
(a+b)(a-b)
a
b
最后结果
(y+3)(y-3)
(a+3b)(a-3b)
(1-5b)(1+5b)
(-x+2)(-x-2)
y
3
a
3b
1
5b
-x
2
尝试应用
概括总结
(2)等式右边是这两个数(字母)的平方差.
平方差公式的特征:
(1)等式左边是两个数(字母)的和乘以这两个数(字母)的差.
注:必须符合平方差
公式特征的代数式才能
用平方差公式
公式中的字母的意义很广泛,可以代表常数,单项式或多项式
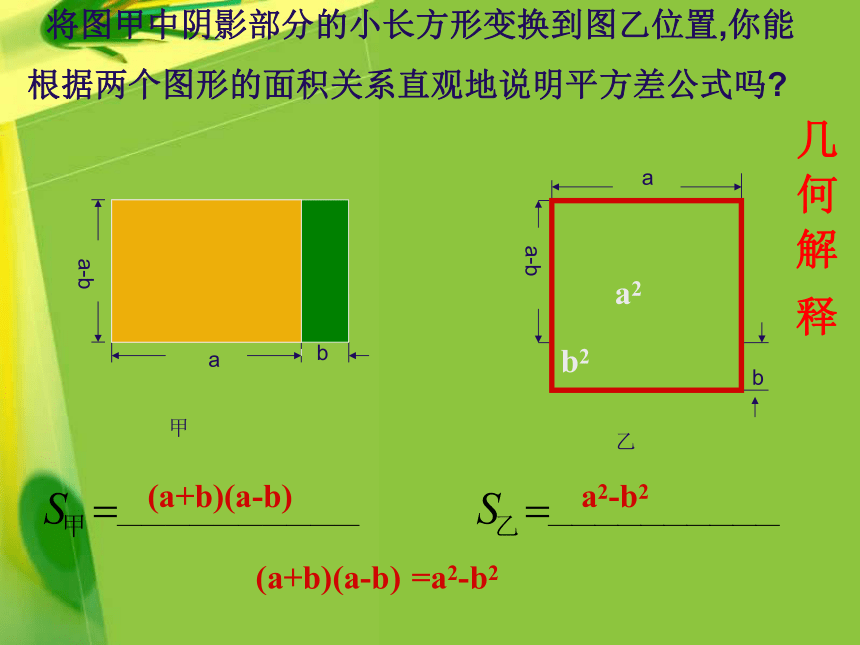
将图甲中阴影部分的小长方形变换到图乙位置,你能
根据两个图形的面积关系直观地说明平方差公式吗?
a-b
a
b
甲
b
a-b
a
乙
(a+b)(a-b)
a2-b2
b2
a2
(a+b)(a-b)
=a2-b2
几
何
解
释
例1
运用平方差公式计算:
(1)
(3x+5y)(3x-5y)
=____2
–
____2
=________
(3x)
(5y)
9x2-25y2
步骤:1、判断;2、调整;3、用公式。
找出相等的“项”和符号相反的“项”,然后应用公式.
×
×
(1)
(2x-3y)(
)=
4x2-9y2
2x+3y
3.填空:
(2)(
+3a)(
-3a)=
4-9a2
±2
±2
4、下列式子中哪些可以用平方差公式运算?如果可以,并计算.
⑴
(ab-8)(ab+8)
⑵
⑶
(2+a)(a-2)
⑷
(3a+2b)(3a-2b)
⑸
(-4k+3)(-4k-3)
⑹
(1-x)(-x-1)
⑺
(-x-1)(x+1)
⑻
(x+3)(x-2)
可以
可以
可以
可以
可以
可以
不可以
不可以
例2
用平方差公式计算:
103×97
(2)59.8×60.2
=(100+3)(100-3)
=1002-32
=10000-9
=9991
=(60-0.2)(60+0.2)
=602-0.22
=3600-0.4
=3599.96
(1)
(4)
(6)
(5)
(2)
(3)
运用平方差公式计算:
运用平方差公式计算:
5678×5680-56792
=(5679-1)(5679+1)-56792
=56792
-1
-56792
=
-1
利用平方差公式计算:
(2+1)(22+1)(24+1)(28+1)+1
=(2-1)(2+1)(22+1)(24+1)(28+1)+1
=(22-1)(22+1)(24+1)(28+1)+1
=(24-1)(24+1)(28+1)+1
=(28-1)(28+1)+1
=216-1+1
=216
一养鸡专业户改建一个边长为
a(m)的正方形养鸡场,计划纵向扩大3m,横向缩短3m,改建为长方形养鸡场.问改建后的养鸡场面积有没有变化?如果有变化,变化多少?
原正方形的面积=
a2
改建后的长方形的面积=
(a+3)(a-3)=a2-9
(a+3)(a-3)-a2
=
a2
-9-a2
=9
如果A=1234567892,
B=123456788×123456790,
试比较A与B的大小.
若m,n为有理数,式子
的值与n有关吗?试说明理由.
试用语言表述平方差公式
(a+b)(a?b)=a2?b2。
应用平方差公式时要注意一些什么?
两数和与这两数差的积,等于它们的平方差。
2.运用平方差公式简便计算:
992
-
1
3.已知x2-y2=8,x-y=4,则x+y的值为___.
2
?
?
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
计算下列各题:
(a+2)(a-2)=________________
(3-x)(3+x)=________________
(a+b)(a-b
)=________________
(4)
(2m+n)(2m-n)=_______________
比较等号两边的代数式,它们在系数和字母方面各有什么特点?两者有什么联系?
知识复习:
多项式与多项式相乘的法则:
(a+n)(b+m)=
ab
+nb
+am
+nm
观察
&
发现
?
观察以上算式及其运算结果,你发现了什么规律?
用自己的语言叙述你的发现.
两数和与这两数差的积,等于这两数的平方的差.
平方差公式:
即两数和与这两数差的积等于这两个数的平方差.
公式中的a,b可以是数,还可以是单项式或多项式
(a+b)(a-b)
a
b
最后结果
(y+3)(y-3)
(a+3b)(a-3b)
(1-5b)(1+5b)
(-x+2)(-x-2)
y
3
a
3b
1
5b
-x
2
尝试应用
概括总结
(2)等式右边是这两个数(字母)的平方差.
平方差公式的特征:
(1)等式左边是两个数(字母)的和乘以这两个数(字母)的差.
注:必须符合平方差
公式特征的代数式才能
用平方差公式
公式中的字母的意义很广泛,可以代表常数,单项式或多项式
将图甲中阴影部分的小长方形变换到图乙位置,你能
根据两个图形的面积关系直观地说明平方差公式吗?
a-b
a
b
甲
b
a-b
a
乙
(a+b)(a-b)
a2-b2
b2
a2
(a+b)(a-b)
=a2-b2
几
何
解
释
例1
运用平方差公式计算:
(1)
(3x+5y)(3x-5y)
=____2
–
____2
=________
(3x)
(5y)
9x2-25y2
步骤:1、判断;2、调整;3、用公式。
找出相等的“项”和符号相反的“项”,然后应用公式.
×
×
(1)
(2x-3y)(
)=
4x2-9y2
2x+3y
3.填空:
(2)(
+3a)(
-3a)=
4-9a2
±2
±2
4、下列式子中哪些可以用平方差公式运算?如果可以,并计算.
⑴
(ab-8)(ab+8)
⑵
⑶
(2+a)(a-2)
⑷
(3a+2b)(3a-2b)
⑸
(-4k+3)(-4k-3)
⑹
(1-x)(-x-1)
⑺
(-x-1)(x+1)
⑻
(x+3)(x-2)
可以
可以
可以
可以
可以
可以
不可以
不可以
例2
用平方差公式计算:
103×97
(2)59.8×60.2
=(100+3)(100-3)
=1002-32
=10000-9
=9991
=(60-0.2)(60+0.2)
=602-0.22
=3600-0.4
=3599.96
(1)
(4)
(6)
(5)
(2)
(3)
运用平方差公式计算:
运用平方差公式计算:
5678×5680-56792
=(5679-1)(5679+1)-56792
=56792
-1
-56792
=
-1
利用平方差公式计算:
(2+1)(22+1)(24+1)(28+1)+1
=(2-1)(2+1)(22+1)(24+1)(28+1)+1
=(22-1)(22+1)(24+1)(28+1)+1
=(24-1)(24+1)(28+1)+1
=(28-1)(28+1)+1
=216-1+1
=216
一养鸡专业户改建一个边长为
a(m)的正方形养鸡场,计划纵向扩大3m,横向缩短3m,改建为长方形养鸡场.问改建后的养鸡场面积有没有变化?如果有变化,变化多少?
原正方形的面积=
a2
改建后的长方形的面积=
(a+3)(a-3)=a2-9
(a+3)(a-3)-a2
=
a2
-9-a2
=9
如果A=1234567892,
B=123456788×123456790,
试比较A与B的大小.
若m,n为有理数,式子
的值与n有关吗?试说明理由.
试用语言表述平方差公式
(a+b)(a?b)=a2?b2。
应用平方差公式时要注意一些什么?
两数和与这两数差的积,等于它们的平方差。
2.运用平方差公式简便计算:
992
-
1
3.已知x2-y2=8,x-y=4,则x+y的值为___.
2
