吉林省洮南市第一中学2021-2022学年高一上学期第一次月考数学(文)试题(Word版含答案)
文档属性
| 名称 | 吉林省洮南市第一中学2021-2022学年高一上学期第一次月考数学(文)试题(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 762.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-29 16:19:07 | ||
图片预览


文档简介
洮南一中2021~2022学年度上学期高一第一次月考
数学试题(文科)
说明:
本试卷分第I卷(选择题)和第II卷(非选择题)两部分,共4页,
22个小题,全卷满分150分,考试时间为120分钟.考试结束后,只交答题卡.
第
I
卷(选择题,共60分)
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合,集合,则等于
(
)
2.命题“ xR, n0N
,使得n0≥2x+1”的否定形式是
(
)
xR, n0N
,使得n0<2x+1
xR, n0N
,使得n0<2x+1
x0R, nN
,使得n<2x0+1
x0R, nN
,使得n<2x0+1
3.下列说法正确的是
(
)
某人月收入x元不高于2000元可表示为“”
小明的身高为x,小华的身高为y,则小明比小华矮可表示为“”
变量x不小于a可表示为“”
变量y不超过a可表示为“”
4.已知集合,那么“”是“”的
(
)
充分不必要条件
必要不充分条件
充要条件
既不充分也不必要条件
5.为全集,是集合,则“存在集合使得”是“”的(
)
充分不必要条件
必要不充分条件
充要条件
既不充分也不必要条件
6.下面说法错误的是
(
)
若,则
若,则
若,则
若为正数,则
7.满足的集合的个数为
(
)
8
7
4
16
8.已知,则
(
)
有最大值
有最小值
有最小值
有最大值
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
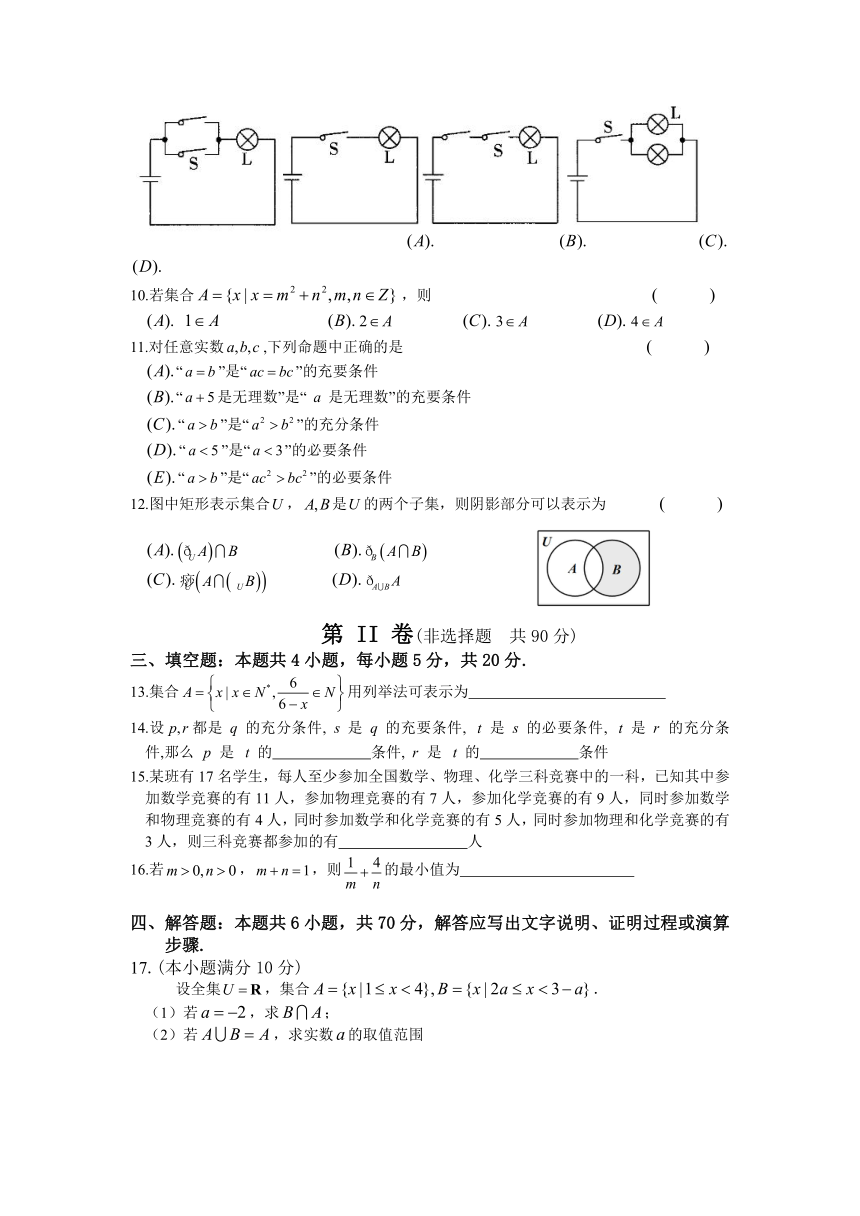
9.设计如图所示的四个电路图,若开关S闭合,灯泡L亮,则符合p是q的充要条件的电路图是
(
)
10.若集合,则
(
)
11.对任意实数,下列命题中正确的是
(
)
“”是“”的充要条件
“是无理数”是“是无理数”的充要条件
“”是“”的充分条件
“”是“”的必要条件
“”是“”的必要条件
12.图中矩形表示集合,是的两个子集,则阴影部分可以表示为
(
)
第
II
卷(非选择题
共90分)
三、填空题:本题共4小题,每小题5分,共20分.
13.集合用列举法可表示为
14.设都是的充分条件,是的充要条件,是的必要条件,是的充分条件,那么是的
条件,是的
条件
15.某班有17名学生,每人至少参加全国数学、物理、化学三科竞赛中的一科,已知其中参加数学竞赛的有11人,参加物理竞赛的有7人,参加化学竞赛的有9人,同时参加数学和物理竞赛的有4人,同时参加数学和化学竞赛的有5人,同时参加物理和化学竞赛的有3人,则三科竞赛都参加的有
人
16.若,,则的最小值为
四、解答题:本题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分10分)
设全集,集合.
(1)若,求;
(2)若,求实数的取值范围
18.(本小题满分12分)
设是由一些实数构成的集合,若a∈A,则,且,
(1)若,求.
(2)证明:若,则
19.(本小题满分12分)
证明:当时,
20.(本小题满分12分)
已知集合.
(1).若,求实数的取值范围.
(2).若,求实数的取值范围
21.(本小题满分12分)
已知命题,,命题,.
(1)若命题和命题q有且只有一个为真命题,求实数a的取值范围;
(2)若命题p和命题q至少有一个为真命题,求实数a的取值范围.
22.(本小题满分12分)
某农户计划利用一面院墙(足够长)和篱笆围出6间一样大小的矩形养鸡场(如图所示)
(1)若农户现有总长度为120米的篱笆材料,则怎样围才能使总面积最大 最大面积是多少
(2)若农户需要围一个总面积为720平方米的养鸡场,则怎样围才能使所用篱笆材料的总长度最短?最短长度为多少?(假设在建造过程中没有浪费所用材料)()
2021~2022学年度上学期高一第一次月考
文科数学参考答案
1、选择题(5×8=40分)(单选题:每个5分)
1
2
3
4
5
6
7
8
B
D
C
B
C
B
A
D
2、选择题(5×4=20分)(多选题:全部选对的得5分,部分选对的得2分,有选错的得0分)
9
10
11
12
BD
ABD
BDE
ABD
三、填空题(5×4=20分)
13.
14.
充分;充要
15.
2
16.
9
三、解答题:(70分)
17.
(本小题满分10分)
解:(1)
若,则,又,所以.
(2)
若,则.
当时,,;
当时,由,解得.
综上可知,实数的取值范围.
18.
(本小题满分12分)
解
(1)因为3∈A,所以,所以,所以,所以.
(2)因为a∈A,所以,所以
19
(本小题满分12分)
解:由题意,知
因为,
所以,,,
所以,
即.
20
(本小题满分12分)
(1).①时,,
② 时,即且,
综上的取值范围为.
(2).由,得,
①时,,
②时,由,解得或.
由第一小题可知,当时,不成立,
当且时,解得成立.
综上,的取值范围为.
21
(本小题满分12分)
解:(1)若命题,为真命题,则,即.
所以若为真命题,则.
若命题,为真命题,则,即.
若为真命题,则.
①当为真,q为假时,为真,即所以;
②当为假,q为真时,p为真,即无解,舍去.
综上所述,当命题和命题q有且只有一个为真命题时,a的取值范围为.
(2)解法一:①当p真q假时,为真,即所以;
②当p假q真时,为真,即所以;
③当p真q真时,无解,舍去.
综上所述,a的取值范围为或.
解法二:考虑p,q至少有一个为真命题的反面,即p,q均为假命题,
即为真,且为真,则解得,即,
故p,q至少有一个为真命题时,a的取值范围为的补集.
故a的取值范围为或.
22.
(本小题满分12分)
解:(1)由题中图形,设每个小矩形的长为米,宽为米,间矩形养鸡场的总面积为平方米;
则,且.因,解得且;
由均值不等式得,解出,得,
当且仅当,即时,;故.
因此当每个小矩形的长为米,宽为米时,养鸡场总面积最大为平方米.
法2:因,,即定值;则;
当且仅当,即时,平方米.)
(2)因养鸡场总面积即为定值;
则篱笆料的长度;
当且仅当且时,
因,解出.
故当小矩形的长为12.64米,宽为9.48米时,最短篱笆料的长度为151.68米.
数学试题(文科)
说明:
本试卷分第I卷(选择题)和第II卷(非选择题)两部分,共4页,
22个小题,全卷满分150分,考试时间为120分钟.考试结束后,只交答题卡.
第
I
卷(选择题,共60分)
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合,集合,则等于
(
)
2.命题“ xR, n0N
,使得n0≥2x+1”的否定形式是
(
)
xR, n0N
,使得n0<2x+1
xR, n0N
,使得n0<2x+1
x0R, nN
,使得n<2x0+1
x0R, nN
,使得n<2x0+1
3.下列说法正确的是
(
)
某人月收入x元不高于2000元可表示为“”
小明的身高为x,小华的身高为y,则小明比小华矮可表示为“”
变量x不小于a可表示为“”
变量y不超过a可表示为“”
4.已知集合,那么“”是“”的
(
)
充分不必要条件
必要不充分条件
充要条件
既不充分也不必要条件
5.为全集,是集合,则“存在集合使得”是“”的(
)
充分不必要条件
必要不充分条件
充要条件
既不充分也不必要条件
6.下面说法错误的是
(
)
若,则
若,则
若,则
若为正数,则
7.满足的集合的个数为
(
)
8
7
4
16
8.已知,则
(
)
有最大值
有最小值
有最小值
有最大值
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.设计如图所示的四个电路图,若开关S闭合,灯泡L亮,则符合p是q的充要条件的电路图是
(
)
10.若集合,则
(
)
11.对任意实数,下列命题中正确的是
(
)
“”是“”的充要条件
“是无理数”是“是无理数”的充要条件
“”是“”的充分条件
“”是“”的必要条件
“”是“”的必要条件
12.图中矩形表示集合,是的两个子集,则阴影部分可以表示为
(
)
第
II
卷(非选择题
共90分)
三、填空题:本题共4小题,每小题5分,共20分.
13.集合用列举法可表示为
14.设都是的充分条件,是的充要条件,是的必要条件,是的充分条件,那么是的
条件,是的
条件
15.某班有17名学生,每人至少参加全国数学、物理、化学三科竞赛中的一科,已知其中参加数学竞赛的有11人,参加物理竞赛的有7人,参加化学竞赛的有9人,同时参加数学和物理竞赛的有4人,同时参加数学和化学竞赛的有5人,同时参加物理和化学竞赛的有3人,则三科竞赛都参加的有
人
16.若,,则的最小值为
四、解答题:本题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分10分)
设全集,集合.
(1)若,求;
(2)若,求实数的取值范围
18.(本小题满分12分)
设是由一些实数构成的集合,若a∈A,则,且,
(1)若,求.
(2)证明:若,则
19.(本小题满分12分)
证明:当时,
20.(本小题满分12分)
已知集合.
(1).若,求实数的取值范围.
(2).若,求实数的取值范围
21.(本小题满分12分)
已知命题,,命题,.
(1)若命题和命题q有且只有一个为真命题,求实数a的取值范围;
(2)若命题p和命题q至少有一个为真命题,求实数a的取值范围.
22.(本小题满分12分)
某农户计划利用一面院墙(足够长)和篱笆围出6间一样大小的矩形养鸡场(如图所示)
(1)若农户现有总长度为120米的篱笆材料,则怎样围才能使总面积最大 最大面积是多少
(2)若农户需要围一个总面积为720平方米的养鸡场,则怎样围才能使所用篱笆材料的总长度最短?最短长度为多少?(假设在建造过程中没有浪费所用材料)()
2021~2022学年度上学期高一第一次月考
文科数学参考答案
1、选择题(5×8=40分)(单选题:每个5分)
1
2
3
4
5
6
7
8
B
D
C
B
C
B
A
D
2、选择题(5×4=20分)(多选题:全部选对的得5分,部分选对的得2分,有选错的得0分)
9
10
11
12
BD
ABD
BDE
ABD
三、填空题(5×4=20分)
13.
14.
充分;充要
15.
2
16.
9
三、解答题:(70分)
17.
(本小题满分10分)
解:(1)
若,则,又,所以.
(2)
若,则.
当时,,;
当时,由,解得.
综上可知,实数的取值范围.
18.
(本小题满分12分)
解
(1)因为3∈A,所以,所以,所以,所以.
(2)因为a∈A,所以,所以
19
(本小题满分12分)
解:由题意,知
因为,
所以,,,
所以,
即.
20
(本小题满分12分)
(1).①时,,
② 时,即且,
综上的取值范围为.
(2).由,得,
①时,,
②时,由,解得或.
由第一小题可知,当时,不成立,
当且时,解得成立.
综上,的取值范围为.
21
(本小题满分12分)
解:(1)若命题,为真命题,则,即.
所以若为真命题,则.
若命题,为真命题,则,即.
若为真命题,则.
①当为真,q为假时,为真,即所以;
②当为假,q为真时,p为真,即无解,舍去.
综上所述,当命题和命题q有且只有一个为真命题时,a的取值范围为.
(2)解法一:①当p真q假时,为真,即所以;
②当p假q真时,为真,即所以;
③当p真q真时,无解,舍去.
综上所述,a的取值范围为或.
解法二:考虑p,q至少有一个为真命题的反面,即p,q均为假命题,
即为真,且为真,则解得,即,
故p,q至少有一个为真命题时,a的取值范围为的补集.
故a的取值范围为或.
22.
(本小题满分12分)
解:(1)由题中图形,设每个小矩形的长为米,宽为米,间矩形养鸡场的总面积为平方米;
则,且.因,解得且;
由均值不等式得,解出,得,
当且仅当,即时,;故.
因此当每个小矩形的长为米,宽为米时,养鸡场总面积最大为平方米.
法2:因,,即定值;则;
当且仅当,即时,平方米.)
(2)因养鸡场总面积即为定值;
则篱笆料的长度;
当且仅当且时,
因,解出.
故当小矩形的长为12.64米,宽为9.48米时,最短篱笆料的长度为151.68米.
同课章节目录
