22.3实际问题与二次函数-同步练习-2021-2022学年人教版九年级数学上册(Word版 含答案)
文档属性
| 名称 | 22.3实际问题与二次函数-同步练习-2021-2022学年人教版九年级数学上册(Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 746.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-30 00:00:00 | ||
图片预览




文档简介
2021-2022学年九年级数学上册同步(人教版)
22.3实际问题与二次函数(2)-同步练习
时间:60分钟
一、单选题
1.飞机着陆后滑行的距离y(单位:m)关于滑行时间以(单位:)的函数解析式是y=60t﹣t2.在飞机着陆滑行中,滑行最后的150m所用的时间是( )s.
A.10
B.20
C.30
D.10或30
2.小红把班级勤工助学挣得的班费500元按一年期存入银行,已知年利率为x,一年到期后银行将本金和利息自动按一年定期转存,设两年到期后,本、利和为y元,则y与x之间的函数关系式为(
)
A.y=500(x+1)2
B.y=x2+500
C.y=x2+500x
D.y=x2+5x
3.某广场有一喷水池,水从地面喷出,如图,以水平地面为x轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线y=-x2+4x(单位:米)的一部分,则水喷出的最大高度是( )
A.4米
B.3米
C.2米
D.1米
4.共享单车为市民出行带来了方便,某单车公司第一个月投放a辆单车,计划第三个月投放单车y辆,设该公司第二、三两个月投放单车数量的月平均增长率为x,那么y与x的函数关系是(
)
A.y=x2+a
B.y=a(1+x)2
C.y=(1﹣x)2+a
D.y=a(1﹣x)2
5.某公园有一个圆形喷水池,喷出的水流的高度h(单位:m)与水流运动时间t(单位:s)之间的关系式为,那么水流从喷出至回落到地面所需要的时间是( )
A.6 s
B.4 s
C.3 s
D.2 s
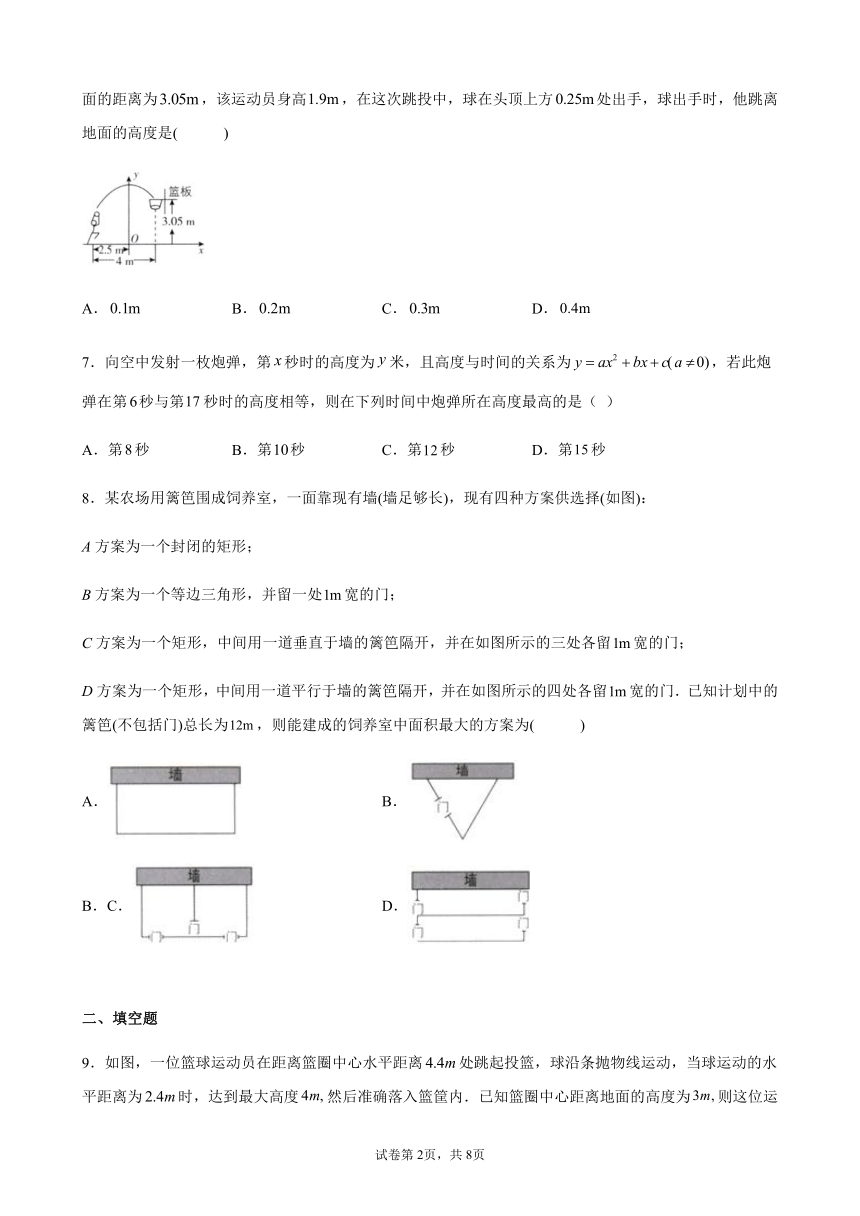
6.一位运动员在距篮筐正下方水平距离处跳起投篮,球运行的路线是抛物线,当球运行的水平距离为时,达到最大高度,然后准确落入篮筐.如图所示,建立平面直角坐标系,已知篮筐中心到地面的距离为,该运动员身高,在这次跳投中,球在头顶上方处出手,球出手时,他跳离地面的高度是( )
A.
B.
C.
D.
7.向空中发射一枚炮弹,第秒时的高度为米,且高度与时间的关系为,若此炮弹在第秒与第秒时的高度相等,则在下列时间中炮弹所在高度最高的是(
)
A.第秒
B.第秒
C.第秒
D.第秒
8.某农场用篱笆围成饲养室,一面靠现有墙(墙足够长),现有四种方案供选择(如图):
A方案为一个封闭的矩形;
B方案为一个等边三角形,并留一处宽的门;
C方案为一个矩形,中间用一道垂直于墙的篱笆隔开,并在如图所示的三处各留宽的门;
D方案为一个矩形,中间用一道平行于墙的篱笆隔开,并在如图所示的四处各留宽的门.已知计划中的篱笆(不包括门)总长为,则能建成的饲养室中面积最大的方案为( )
B.
C.
D.
二、填空题
9.如图,一位篮球运动员在距离篮圈中心水平距离处跳起投篮,球沿条抛物线运动,当球运动的水平距离为时,达到最大高度然后准确落入篮筐内.已知篮圈中心距离地面的高度为则这位运动员投跳时,球出手处距离地面的高度为______.
10.2013年5月26日,中国羽毛球队蝉联苏迪曼杯团体赛冠军,成就了首个五连冠霸业.比赛中羽毛球的某次运动路线可以看作是一条抛物线(如图).若不考虑外力因素,羽毛球行进高度y(米)与水平距离x(米)之间满足关系,则羽毛球飞出的水平距离为
米.
11.竖直上抛某物体时,物体离地面的高度h(m)与运动时间t(s)之间的关系可用公式来表示,由公式可知,该物体经过_____s离地面的高度为30m.
12.某工厂第一年的利润是20万元,第三年的利润是y万元,与平均年增长率x之间的函数关系式是______________.
13.农机厂第一个月水泵的产量为50(台),第三个月的产量y(台)与月平均增长率x之间的关系表示为___________.
14.某体育公园的圆形喷水池的水柱如图①所示,如果曲线APB表示落点B离点O最远的一条水流(如图②),其上的水珠的高度y(米)关于水平距离x(米)的函数解析式为y=-x2+4x+,那么圆形水池的半径至少为_______米时,才能使喷出的水流不落在水池外.
15.小林家的洗手台面上有一瓶洗手液(如图1),当手按住顶部A下压时(如图2),洗手液瞬间从喷口B流出,已知瓶子上部分的和的圆心分别为D,C,下部分的视图是矩形CGHD,GH=10cm,GC=8cm,点E到台面GH的距离为14cm,点B距台面GH的距离为16cm,且B,D,H三点共线.如果从喷口B流出的洗手液路线呈抛物线形,且该路线所在的抛物线经过C.E两点,接洗手液时,当手心O距DH的水平距离为2cm时,手心O距水平台面GH的高度为_____cm.
16.两幢大楼的部分截面及相关数据如图,小明在甲楼A处透过窗户E发现乙楼F处出现火灾,此时A,E,F在同一直线上.跑到一楼时,消防员正在进行喷水灭火,水流路线呈抛物线,在1.2m高的D处喷出,水流正好经过E,F.
若点B和点E、点C和F的离地高度分别相同,现消防员将水流抛物线向上平移0.4m,再向左后退了____m,恰好把水喷到F处进行灭火.
三、解答题
17.某公司的生产利润原来是万元,经过连续两年的增长达到了万元,如果每年增长率都是,写出利润与增长的百分率之间的函数解析式,它是什么函数?
18.在美化校园的活动中,某兴趣小组用总长为米的围栏材料,一面靠墙,围成一个矩形花园,墙长米,设的长为米,矩形花园的面积为平方米,当为多少时,取得最大值,最大值是多少?
如图所示,公园要造圆形的喷水池,在水池中央垂直于水面处安装一个柱子OA,O恰在水面中心,OA=1.25m,由柱子顶端A处的喷头向外喷水,水流在各个方向沿形状相同的抛物线路线落下,为使水流形状较为漂亮,要求设计成水流在离OA距离为1m处达到距水面距离最大,高度2.25m.若不计其他因素,那么水池的半径至少要多少米才能使喷出的水流不致落到池外
20.某企业投资100万元引进一条新产品加工线,若不计维修、保养费用,预计投产后每年可创利33万元,该生产线投产后,从第1年到第年的维修、保养费用累计为万元,其情况如图所示,可以看出图中的折线近似于过原点的抛物线的一部分.
(1)求过、、三点的函数解析式.
(2)利用(1)的结果预测第4年的维修、保养费用,并说明第4年是否能收回投资并开始赢利?
21.某大学生创业团队抓住商机,购进一批干果分装成营养搭配合理的小包装后出售,每袋成本3元.试销期间发现每天的销售量(袋与销售单价(元之间满足一次函数关系,部分数据如表所示,其中3.5≤x≤5.5.另外每天还需支付其他各项费用80元.
销售单价(元
3.5
5.5
销售量(袋
280
120
(1)请求出与之间的函数关系式;
(2)设每天的利润为元,当销售单价定为多少元时,每天的利润最大?最大利润是多少元?
22.某广场喷泉的喷嘴安装在平地上.有一喷嘴喷出的水流呈抛物线状,喷出的水流高度y(m)与喷出水流喷嘴的水平距离x(m)之间满足
(l)喷嘴能喷出水流的最大高度是多少?
(2)喷嘴喷出水流的最远距离为多少?
23.如图,一名男生推铅球,铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系是.求:
(1)铅球在行进中的最大高度;
(2)该男生将铅球推出的距离是多少m?
24.在一次篮球比赛中,如图,队员甲正在投篮.已知球出手时离地面,与篮圈中心的水平距离为,球出手后水平距离为时达到最大高度,设篮球运行轨迹为抛物线,篮圈距地面.
(1)建立如图所示的平面直角坐标系,求此抛物线的解析式;
(2)此时球能否准确投中?
(3)此时,对方队员乙在甲面前处跳起盖帽拦截,已知乙的最大摸高为,那么他能否获得成功?
试卷第1页,共3页
参考答案
1.A
【解析】解:当y取得最大值时,飞机停下来,
则y=60t﹣1.5t2=﹣1.5(t﹣20)2+600,
此时t=20,飞机着陆后滑行600米才能停下来.
因此t的取值范围是0≤t≤20;
即当y=600﹣150=450时,
即60t﹣t2=450,
解得:t=10,t=30(不合题意舍去),
∴滑行最后的150m所用的时间是20﹣10=10,
故选:A.
2.A
【解析】一年后的本息和为500(1+x),这也是第二年的本金,
所以两年后的本息和y=500(1+x)2.
故选A.
3.A
【解析】)∵y=-x2+4x=,
∴当x=2时,y有最大值4,
∴最大高度为4m
4.B
【解析】解:设该公司第二、三两个月投放单车数量的月平均增长率为x,
依题意得第三个月第三个月投放单车a(1+x)2辆,
则y=a(1+x)2.
故选:B.
5.A
【解析】由于水流从抛出至回落到地面时高度h为0,把h=0代入h=30t-5t2即可求出t,也就求出了水流从抛出至回落到地面所需要的时间.
解:水流从抛出至回落到地面时高度h为0,
把h=0代入h=30t 5t2得:5t2 30t=0,
解得:t1=0(舍去),t2=6.
故水流从抛出至回落到地面所需要的时间6s.
故选A.
6.A
【解析】∵当球运行的水平距离为时,达到最大高度,∴抛物线的顶点坐标为,∴设抛物线的解析式为.由题意知图象过点,∴,解得,抛物线的解析式为.设球出手时,他跳离地面的高度为.
∵抛物线的解析式为,球出手时,球的高度为.
∴,∴.
故选:A.
7.C
【解析】解:根据题意,炮弹在第秒与第秒时的高度相等,
∴抛物线的对称轴为:秒,
∵第12秒距离对称轴最近,
∴上述时间中,第12秒时炮弹高度最高;
故选:C.
8.C
【解析】设建成的饲养室的面积为,
对于A选项,如图(1),设边的长为,则,
,
,
由矩形的面积公式得:,
则在范围内,当时,取得最大值,最大值为18;
对于B选项,如图(2),设,则,解得,
由等边三角形的性质得:AB边上的高为,
则;
对于C选项,如图(3),设,则,,
,
,
由矩形的面积公式得:,
则在范围内,当时,取得最大值,最大值为;
对于D选项,如图(4),设,则,
,
,
由矩形的面积公式得:,
则在范围内,当时,取得最大值,最大值为16;
因为,
所以建成的饲养室中面积最大的方案是C方案,
故选:C.
9.2.56
【解析】解:设球的运动轨迹y=ax2+c,
4.4-2.4=2,
∴y=ax2+c经过点(0,4),(2,3),
代入可得:,
解得:,
∴,
当x=-2.4时,,
即球出手处距离地面的高度为2.56m,
故答案为:2.56m.
10.5
【解析】当y=0时,,
解得:x1=﹣1(舍),x2=5.
∴羽毛球飞出的水平距离为5米.
11.2或3
【解析】解:设该物体经过ts离地面的高度为30m
则整理得:
解得:t=2或3
12.
【解析】解:设增产率为x,因为第一年的利润是20万元,所以第二年的利润是20(1+x),第三年的利润是20(1+x)(1+x),即20(1+x)2,依题意得函数关系式:
y=20(1+x)2=20x2+40x+20
(x>0)
故答案为y=20x2+40x+20
(x>0).
13.
【解析】第二个月是50(1+x),
第三个月是50(1+x)2
所以答案为y=50(1+x)2
14.
【解析】当y=0时,即-x2+4x+=0,
解得x1=,x2=-(舍去).
答:水池的半径至少米时,才能使喷出的水流不落在水池外.
故答案是:.
15.11.
【解析】如图:
由题意可知:CD=DE=10cm,
根据题意,得C(﹣5,8),E(﹣3,14),B(5,16).
设抛物线解析式为y=ax2+bx+c,
因为抛物线经过C、E、B三点,
∴,
解得,
所以抛物线解析式为y=-x2+x+.
当x=7时,y=11,
∴Q(7,11),
所以手心O距水平台面GH的高度为11cm.
故答案为11.
16.
【解析】设直线AE的解析式为:y=kx+21.2.
把E(20,9.2)代入得,20k+21.2=9.2,
∴k=-0.6,
∴y=-0.6x+21.2.
把y=6.2代入得,
-0.6x+21.2=6.2,
∴x=25,
∴F(25,6.2).
设抛物线解析式为:y=ax2+bx+1.2,
把E(20,9.2),
F(25,6.2)代入得,
,解之得:,
∴y=-0.04x2+1.2x+1.2,
设向上平移0.4m,向左后退了hm,
恰好把水喷到F处进行灭火由题意得
y=-0.04(x+h)2+1.2(x+h)+1.2+0.4,
把F(25,6.2)代入得,
6.2=-0.04×(25+h)2+1.2(25+h)+1.2+0.4,整理得:h2+20h-10=0,
解之得:
,(舍去).
∴向后退了m
故答案是:
17.见解析.
【解析】依题意,得:,
此函数是二次函数.
18.80
【解析】.
,
当时,有最大值,最大值
19.2.5米
【解析】以地面上任一条直线为x轴,OA为y轴建立直角坐标系,
设y=a(x-1)2+2.25,则当x=0时,y=1.25,故a+2.25=1,a=-1.
由y=0得-(x-1)2+2.25=0,得(x-1)2=2.25,解得x1=2.5,x2=-0.5(舍去)
故水池的半径至少要2.5米.
20.(1);(2)第4年可收回投资.
【解析】解:(1)设,
由题意,时,;时,,分别代入,得解得,,
∴.
(2)当时,(万元),
(万元),
∴第4年的维修、保养费用为7.55万元.
设,
则.
故当时,;当时,万元,故第4年可收回投资.
21.(1)与之间的函数关系式为;
(2)当销售单价定为5元时,每天的利润最大,最大利润是240元.
【解析】解:(1)设.
将,;,代入,
得,解得.
则与之间的函数关系式为.
(2)由题意得:
.
∵3.5≤x≤5.5,
当时,有最大值为240.
故当销售单价定为5元时,每天的利润最大,最大利润是240元.
22.(1)
2m;(2)
4m.
【解析】(1)二次函数y=x2+2x,
y=(x﹣2)2+2,
∴当x=2时,喷嘴喷出水流的最大高度是y=2m;
(2)令y=0,则x2+2x=0,
解得,x1=0,x2=4,
答:喷嘴喷出水流的最远距离为4m.
23.(1)铅球在行进中的最大高度为;(2)该男生把铅球推出的水平距离是.
【解析】(1)
∵
∴y的最大值为3
∴铅球在行进中的最大高度为.
(2)令得:
解方程得,,(负值舍去).
∴该男生把铅球推出的水平距离是.
24.(1);(2)能投中;(3)能拦截成功,理由见解析
【解析】(1)
如图,球出手点、最高点(顶点)坐标分别为:,
设二次函数解析式为,将点代入可得:,
解得:,抛物线解析式为:;
(2)将点横坐标代入抛物线解析式得:
即点在抛物线上,此球一定能投中;
(3)能拦截成功.理由:将代入得
,他能拦截成功.
答案第1页,共2页
答案第1页,共2页
22.3实际问题与二次函数(2)-同步练习
时间:60分钟
一、单选题
1.飞机着陆后滑行的距离y(单位:m)关于滑行时间以(单位:)的函数解析式是y=60t﹣t2.在飞机着陆滑行中,滑行最后的150m所用的时间是( )s.
A.10
B.20
C.30
D.10或30
2.小红把班级勤工助学挣得的班费500元按一年期存入银行,已知年利率为x,一年到期后银行将本金和利息自动按一年定期转存,设两年到期后,本、利和为y元,则y与x之间的函数关系式为(
)
A.y=500(x+1)2
B.y=x2+500
C.y=x2+500x
D.y=x2+5x
3.某广场有一喷水池,水从地面喷出,如图,以水平地面为x轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线y=-x2+4x(单位:米)的一部分,则水喷出的最大高度是( )
A.4米
B.3米
C.2米
D.1米
4.共享单车为市民出行带来了方便,某单车公司第一个月投放a辆单车,计划第三个月投放单车y辆,设该公司第二、三两个月投放单车数量的月平均增长率为x,那么y与x的函数关系是(
)
A.y=x2+a
B.y=a(1+x)2
C.y=(1﹣x)2+a
D.y=a(1﹣x)2
5.某公园有一个圆形喷水池,喷出的水流的高度h(单位:m)与水流运动时间t(单位:s)之间的关系式为,那么水流从喷出至回落到地面所需要的时间是( )
A.6 s
B.4 s
C.3 s
D.2 s
6.一位运动员在距篮筐正下方水平距离处跳起投篮,球运行的路线是抛物线,当球运行的水平距离为时,达到最大高度,然后准确落入篮筐.如图所示,建立平面直角坐标系,已知篮筐中心到地面的距离为,该运动员身高,在这次跳投中,球在头顶上方处出手,球出手时,他跳离地面的高度是( )
A.
B.
C.
D.
7.向空中发射一枚炮弹,第秒时的高度为米,且高度与时间的关系为,若此炮弹在第秒与第秒时的高度相等,则在下列时间中炮弹所在高度最高的是(
)
A.第秒
B.第秒
C.第秒
D.第秒
8.某农场用篱笆围成饲养室,一面靠现有墙(墙足够长),现有四种方案供选择(如图):
A方案为一个封闭的矩形;
B方案为一个等边三角形,并留一处宽的门;
C方案为一个矩形,中间用一道垂直于墙的篱笆隔开,并在如图所示的三处各留宽的门;
D方案为一个矩形,中间用一道平行于墙的篱笆隔开,并在如图所示的四处各留宽的门.已知计划中的篱笆(不包括门)总长为,则能建成的饲养室中面积最大的方案为( )
B.
C.
D.
二、填空题
9.如图,一位篮球运动员在距离篮圈中心水平距离处跳起投篮,球沿条抛物线运动,当球运动的水平距离为时,达到最大高度然后准确落入篮筐内.已知篮圈中心距离地面的高度为则这位运动员投跳时,球出手处距离地面的高度为______.
10.2013年5月26日,中国羽毛球队蝉联苏迪曼杯团体赛冠军,成就了首个五连冠霸业.比赛中羽毛球的某次运动路线可以看作是一条抛物线(如图).若不考虑外力因素,羽毛球行进高度y(米)与水平距离x(米)之间满足关系,则羽毛球飞出的水平距离为
米.
11.竖直上抛某物体时,物体离地面的高度h(m)与运动时间t(s)之间的关系可用公式来表示,由公式可知,该物体经过_____s离地面的高度为30m.
12.某工厂第一年的利润是20万元,第三年的利润是y万元,与平均年增长率x之间的函数关系式是______________.
13.农机厂第一个月水泵的产量为50(台),第三个月的产量y(台)与月平均增长率x之间的关系表示为___________.
14.某体育公园的圆形喷水池的水柱如图①所示,如果曲线APB表示落点B离点O最远的一条水流(如图②),其上的水珠的高度y(米)关于水平距离x(米)的函数解析式为y=-x2+4x+,那么圆形水池的半径至少为_______米时,才能使喷出的水流不落在水池外.
15.小林家的洗手台面上有一瓶洗手液(如图1),当手按住顶部A下压时(如图2),洗手液瞬间从喷口B流出,已知瓶子上部分的和的圆心分别为D,C,下部分的视图是矩形CGHD,GH=10cm,GC=8cm,点E到台面GH的距离为14cm,点B距台面GH的距离为16cm,且B,D,H三点共线.如果从喷口B流出的洗手液路线呈抛物线形,且该路线所在的抛物线经过C.E两点,接洗手液时,当手心O距DH的水平距离为2cm时,手心O距水平台面GH的高度为_____cm.
16.两幢大楼的部分截面及相关数据如图,小明在甲楼A处透过窗户E发现乙楼F处出现火灾,此时A,E,F在同一直线上.跑到一楼时,消防员正在进行喷水灭火,水流路线呈抛物线,在1.2m高的D处喷出,水流正好经过E,F.
若点B和点E、点C和F的离地高度分别相同,现消防员将水流抛物线向上平移0.4m,再向左后退了____m,恰好把水喷到F处进行灭火.
三、解答题
17.某公司的生产利润原来是万元,经过连续两年的增长达到了万元,如果每年增长率都是,写出利润与增长的百分率之间的函数解析式,它是什么函数?
18.在美化校园的活动中,某兴趣小组用总长为米的围栏材料,一面靠墙,围成一个矩形花园,墙长米,设的长为米,矩形花园的面积为平方米,当为多少时,取得最大值,最大值是多少?
如图所示,公园要造圆形的喷水池,在水池中央垂直于水面处安装一个柱子OA,O恰在水面中心,OA=1.25m,由柱子顶端A处的喷头向外喷水,水流在各个方向沿形状相同的抛物线路线落下,为使水流形状较为漂亮,要求设计成水流在离OA距离为1m处达到距水面距离最大,高度2.25m.若不计其他因素,那么水池的半径至少要多少米才能使喷出的水流不致落到池外
20.某企业投资100万元引进一条新产品加工线,若不计维修、保养费用,预计投产后每年可创利33万元,该生产线投产后,从第1年到第年的维修、保养费用累计为万元,其情况如图所示,可以看出图中的折线近似于过原点的抛物线的一部分.
(1)求过、、三点的函数解析式.
(2)利用(1)的结果预测第4年的维修、保养费用,并说明第4年是否能收回投资并开始赢利?
21.某大学生创业团队抓住商机,购进一批干果分装成营养搭配合理的小包装后出售,每袋成本3元.试销期间发现每天的销售量(袋与销售单价(元之间满足一次函数关系,部分数据如表所示,其中3.5≤x≤5.5.另外每天还需支付其他各项费用80元.
销售单价(元
3.5
5.5
销售量(袋
280
120
(1)请求出与之间的函数关系式;
(2)设每天的利润为元,当销售单价定为多少元时,每天的利润最大?最大利润是多少元?
22.某广场喷泉的喷嘴安装在平地上.有一喷嘴喷出的水流呈抛物线状,喷出的水流高度y(m)与喷出水流喷嘴的水平距离x(m)之间满足
(l)喷嘴能喷出水流的最大高度是多少?
(2)喷嘴喷出水流的最远距离为多少?
23.如图,一名男生推铅球,铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系是.求:
(1)铅球在行进中的最大高度;
(2)该男生将铅球推出的距离是多少m?
24.在一次篮球比赛中,如图,队员甲正在投篮.已知球出手时离地面,与篮圈中心的水平距离为,球出手后水平距离为时达到最大高度,设篮球运行轨迹为抛物线,篮圈距地面.
(1)建立如图所示的平面直角坐标系,求此抛物线的解析式;
(2)此时球能否准确投中?
(3)此时,对方队员乙在甲面前处跳起盖帽拦截,已知乙的最大摸高为,那么他能否获得成功?
试卷第1页,共3页
参考答案
1.A
【解析】解:当y取得最大值时,飞机停下来,
则y=60t﹣1.5t2=﹣1.5(t﹣20)2+600,
此时t=20,飞机着陆后滑行600米才能停下来.
因此t的取值范围是0≤t≤20;
即当y=600﹣150=450时,
即60t﹣t2=450,
解得:t=10,t=30(不合题意舍去),
∴滑行最后的150m所用的时间是20﹣10=10,
故选:A.
2.A
【解析】一年后的本息和为500(1+x),这也是第二年的本金,
所以两年后的本息和y=500(1+x)2.
故选A.
3.A
【解析】)∵y=-x2+4x=,
∴当x=2时,y有最大值4,
∴最大高度为4m
4.B
【解析】解:设该公司第二、三两个月投放单车数量的月平均增长率为x,
依题意得第三个月第三个月投放单车a(1+x)2辆,
则y=a(1+x)2.
故选:B.
5.A
【解析】由于水流从抛出至回落到地面时高度h为0,把h=0代入h=30t-5t2即可求出t,也就求出了水流从抛出至回落到地面所需要的时间.
解:水流从抛出至回落到地面时高度h为0,
把h=0代入h=30t 5t2得:5t2 30t=0,
解得:t1=0(舍去),t2=6.
故水流从抛出至回落到地面所需要的时间6s.
故选A.
6.A
【解析】∵当球运行的水平距离为时,达到最大高度,∴抛物线的顶点坐标为,∴设抛物线的解析式为.由题意知图象过点,∴,解得,抛物线的解析式为.设球出手时,他跳离地面的高度为.
∵抛物线的解析式为,球出手时,球的高度为.
∴,∴.
故选:A.
7.C
【解析】解:根据题意,炮弹在第秒与第秒时的高度相等,
∴抛物线的对称轴为:秒,
∵第12秒距离对称轴最近,
∴上述时间中,第12秒时炮弹高度最高;
故选:C.
8.C
【解析】设建成的饲养室的面积为,
对于A选项,如图(1),设边的长为,则,
,
,
由矩形的面积公式得:,
则在范围内,当时,取得最大值,最大值为18;
对于B选项,如图(2),设,则,解得,
由等边三角形的性质得:AB边上的高为,
则;
对于C选项,如图(3),设,则,,
,
,
由矩形的面积公式得:,
则在范围内,当时,取得最大值,最大值为;
对于D选项,如图(4),设,则,
,
,
由矩形的面积公式得:,
则在范围内,当时,取得最大值,最大值为16;
因为,
所以建成的饲养室中面积最大的方案是C方案,
故选:C.
9.2.56
【解析】解:设球的运动轨迹y=ax2+c,
4.4-2.4=2,
∴y=ax2+c经过点(0,4),(2,3),
代入可得:,
解得:,
∴,
当x=-2.4时,,
即球出手处距离地面的高度为2.56m,
故答案为:2.56m.
10.5
【解析】当y=0时,,
解得:x1=﹣1(舍),x2=5.
∴羽毛球飞出的水平距离为5米.
11.2或3
【解析】解:设该物体经过ts离地面的高度为30m
则整理得:
解得:t=2或3
12.
【解析】解:设增产率为x,因为第一年的利润是20万元,所以第二年的利润是20(1+x),第三年的利润是20(1+x)(1+x),即20(1+x)2,依题意得函数关系式:
y=20(1+x)2=20x2+40x+20
(x>0)
故答案为y=20x2+40x+20
(x>0).
13.
【解析】第二个月是50(1+x),
第三个月是50(1+x)2
所以答案为y=50(1+x)2
14.
【解析】当y=0时,即-x2+4x+=0,
解得x1=,x2=-(舍去).
答:水池的半径至少米时,才能使喷出的水流不落在水池外.
故答案是:.
15.11.
【解析】如图:
由题意可知:CD=DE=10cm,
根据题意,得C(﹣5,8),E(﹣3,14),B(5,16).
设抛物线解析式为y=ax2+bx+c,
因为抛物线经过C、E、B三点,
∴,
解得,
所以抛物线解析式为y=-x2+x+.
当x=7时,y=11,
∴Q(7,11),
所以手心O距水平台面GH的高度为11cm.
故答案为11.
16.
【解析】设直线AE的解析式为:y=kx+21.2.
把E(20,9.2)代入得,20k+21.2=9.2,
∴k=-0.6,
∴y=-0.6x+21.2.
把y=6.2代入得,
-0.6x+21.2=6.2,
∴x=25,
∴F(25,6.2).
设抛物线解析式为:y=ax2+bx+1.2,
把E(20,9.2),
F(25,6.2)代入得,
,解之得:,
∴y=-0.04x2+1.2x+1.2,
设向上平移0.4m,向左后退了hm,
恰好把水喷到F处进行灭火由题意得
y=-0.04(x+h)2+1.2(x+h)+1.2+0.4,
把F(25,6.2)代入得,
6.2=-0.04×(25+h)2+1.2(25+h)+1.2+0.4,整理得:h2+20h-10=0,
解之得:
,(舍去).
∴向后退了m
故答案是:
17.见解析.
【解析】依题意,得:,
此函数是二次函数.
18.80
【解析】.
,
当时,有最大值,最大值
19.2.5米
【解析】以地面上任一条直线为x轴,OA为y轴建立直角坐标系,
设y=a(x-1)2+2.25,则当x=0时,y=1.25,故a+2.25=1,a=-1.
由y=0得-(x-1)2+2.25=0,得(x-1)2=2.25,解得x1=2.5,x2=-0.5(舍去)
故水池的半径至少要2.5米.
20.(1);(2)第4年可收回投资.
【解析】解:(1)设,
由题意,时,;时,,分别代入,得解得,,
∴.
(2)当时,(万元),
(万元),
∴第4年的维修、保养费用为7.55万元.
设,
则.
故当时,;当时,万元,故第4年可收回投资.
21.(1)与之间的函数关系式为;
(2)当销售单价定为5元时,每天的利润最大,最大利润是240元.
【解析】解:(1)设.
将,;,代入,
得,解得.
则与之间的函数关系式为.
(2)由题意得:
.
∵3.5≤x≤5.5,
当时,有最大值为240.
故当销售单价定为5元时,每天的利润最大,最大利润是240元.
22.(1)
2m;(2)
4m.
【解析】(1)二次函数y=x2+2x,
y=(x﹣2)2+2,
∴当x=2时,喷嘴喷出水流的最大高度是y=2m;
(2)令y=0,则x2+2x=0,
解得,x1=0,x2=4,
答:喷嘴喷出水流的最远距离为4m.
23.(1)铅球在行进中的最大高度为;(2)该男生把铅球推出的水平距离是.
【解析】(1)
∵
∴y的最大值为3
∴铅球在行进中的最大高度为.
(2)令得:
解方程得,,(负值舍去).
∴该男生把铅球推出的水平距离是.
24.(1);(2)能投中;(3)能拦截成功,理由见解析
【解析】(1)
如图,球出手点、最高点(顶点)坐标分别为:,
设二次函数解析式为,将点代入可得:,
解得:,抛物线解析式为:;
(2)将点横坐标代入抛物线解析式得:
即点在抛物线上,此球一定能投中;
(3)能拦截成功.理由:将代入得
,他能拦截成功.
答案第1页,共2页
答案第1页,共2页
同课章节目录
