23.1 图形的旋转培优训练-2021-2022学年人教版数学九年级上册(Word版 含答案)
文档属性
| 名称 | 23.1 图形的旋转培优训练-2021-2022学年人教版数学九年级上册(Word版 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 599.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-30 00:00:00 | ||
图片预览



文档简介
人教版
九年级数学上册
23.1
图形的旋转
培优训练
一、选择题
1.
在平面直角坐标系中,点P(-4,2)向右平移7个单位长度得到点P1,点P1绕原点逆时针旋转90°得到点P2,则点P2的坐标是( )
A.(-2,3)
B.(-3,2)
C.(2,-3)
D.(3,-2)
2.
观察图,其中可以看成是由“基本图案”通过旋转形成的共有( )
A.1个
B.2个
C.3个
D.4个
3.
如图,点E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置,若四边形AECF的面积为20,DE=2,则AE的长为( )
A.4
B.2
C.6
D.2
4.
如图,将△ABC绕点C顺时针旋转得到△DEC,使点A的对应点D恰好落在边AB上,点B的对应点为E,连接BE,下列结论一定正确的是( )
A.AC=AD
B.AB⊥EB
C.BC=DE
D.∠A=∠EBC
5.
2018·桂林
如图,在正方形ABCD中,AB=3,点M在边CD上,且DM=1,△AEM与△ADM关于AM所在的直线对称,将△ADM绕点A按顺时针方向旋转90°得到△ABF,连接EF,则线段EF的长为( )
A.3
B.2
C.
D.
6.
如图,将△ABC绕点B逆时针旋转α,得到△EBD,若点A恰好在ED的延长线上,则∠CAD的度数为( )
A.90°-α
B.α
C.180°-α
D.2α
7.
2019·河南
如图,在△OAB中,顶点O(0,0),A(-3,4),B(3,4),将△OAB与正方形ABCD组成的图形绕点O顺时针旋转,每次旋转90°,则第70次旋转结束时,点D的坐标为( )
A.(10,3)
B.(-3,10)
C.(10,-3)
D.(3,-10)
8.
如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A′B′C,M是BC的中点,P是A′B′的中点,连接PM.若BC=2,∠A=30°,则线段PM的最大值是( )
A.4
B.3
C.2
D.1
二、填空题
9.
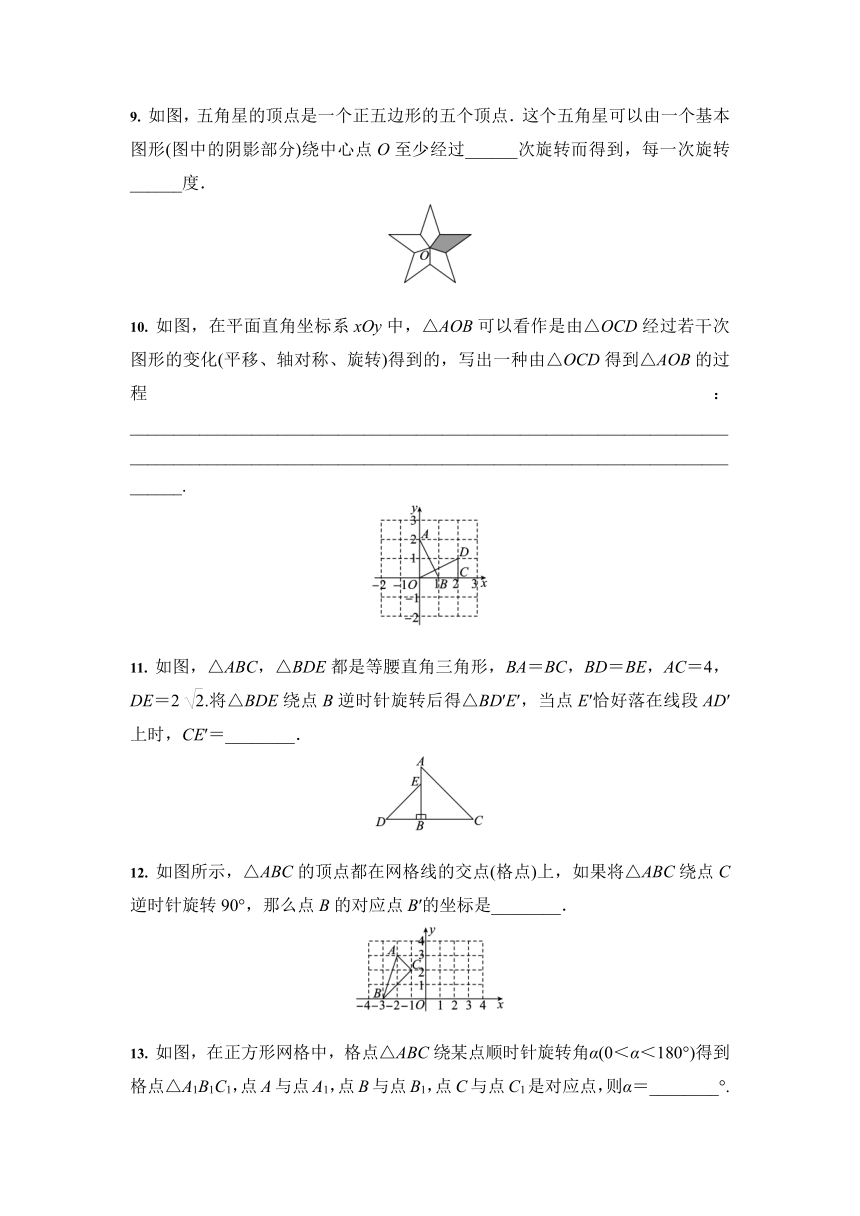
如图,五角星的顶点是一个正五边形的五个顶点.这个五角星可以由一个基本图形(图中的阴影部分)绕中心点O至少经过______次旋转而得到,每一次旋转______度.
10.
如图,在平面直角坐标系xOy中,△AOB可以看作是由△OCD经过若干次图形的变化(平移、轴对称、旋转)得到的,写出一种由△OCD得到△AOB的过程:________________________________________________________________________________________________________________________________________________.
11.
如图,△ABC,△BDE都是等腰直角三角形,BA=BC,BD=BE,AC=4,DE=2
.将△BDE绕点B逆时针旋转后得△BD′E′,当点E′恰好落在线段AD′上时,CE′=________.
12.
如图所示,△ABC的顶点都在网格线的交点(格点)上,如果将△ABC绕点C逆时针旋转90°,那么点B的对应点B′的坐标是________.
13.
如图,在正方形网格中,格点△ABC绕某点顺时针旋转角α(0<α<180°)得到格点△A1B1C1,点A与点A1,点B与点B1,点C与点C1是对应点,则α=________°.
14.
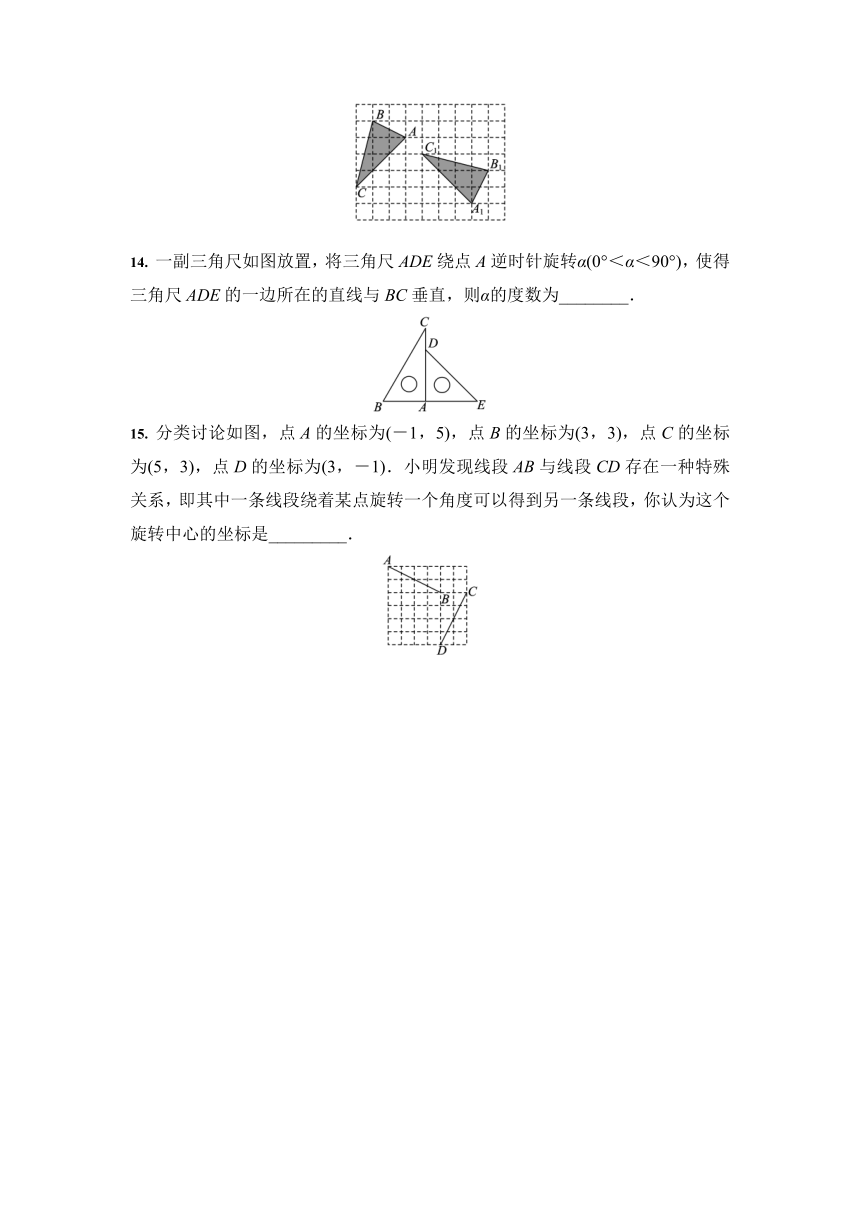
一副三角尺如图放置,将三角尺ADE绕点A逆时针旋转α(0°<α<90°),使得三角尺ADE的一边所在的直线与BC垂直,则α的度数为________.
15.
分类讨论如图,点A的坐标为(-1,5),点B的坐标为(3,3),点C的坐标为(5,3),点D的坐标为(3,-1).小明发现线段AB与线段CD存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,你认为这个旋转中心的坐标是_________.
教师详解详析
16.
2018·陕西
如图,点O是平行四边形ABCD的对称中心,AD>AB,E,F是AB边上的点,且EF=AB;G,H是BC边上的点,且GH=BC.若S1,S2分别表示△EOF和△GOH的面积,则S1与S2之间的等量关系是=________.
三、解答题
17.
如图,在△ABC中,∠ACB=90°,AC=BC,D是AB边上一点(点D与点A,B不重合),连接CD,将线段CD绕点C逆时针旋转90°得到线段CE,连接DE交BC于点F,连接BE.
(1)求证:△ACD≌△BCE;
(2)当AD=BF时,求∠BEF的度数.
18.
如图,在△ABC中,∠BAC=90°,AB=AC,D,E是BC边上的点,将△ABD绕点A逆时针旋转得到△ACD′.
(1)求∠DAD′的度数;
(2)当∠DAE=45°时,求证:DE=D′E.
19.
请认真阅读下面的数学小探究系列,完成所提出的问题:
(1)探究1:如图①,在等腰直角三角形ABC中,∠ACB=90°,BC=a,将边AB绕点B顺时针旋转90°得到线段BD,连接CD.求证:△BCD的面积为a2.(提示:过点D作BC边上的高DE,可证△ABC≌△BDE)
(2)探究2:如图②,在一般的Rt△ABC中,∠ACB=90°,BC=a,将边AB绕点B顺时针旋转90°得到线段BD,连接CD,请用含a的式子表示△BCD的面积,并说明理由.
(3)探究3:如图③,在等腰三角形ABC中,AB=AC,BC=a,将边AB绕点B顺时针旋转90°得到线段BD,连接CD,试探究用含a的式子表示△BCD的面积,要有探究过程.
20.
将一副三角尺按图①摆放,等腰直角三角尺的直角边DF恰好垂直平分AB,与AC相交于点G,BC=2
.
(1)求GC的长;
(2)如图②,将△DEF绕点D顺时针旋转,使直角边DF经过点C,另一直角边DE与AC相交于点H,分别过点H,C作AB的垂线,垂足分别为M,N.通过观察,猜想MD与ND的数量关系,并验证你的猜想;
(3)在(2)的条件下,将△DEF沿DB方向平移得到△D′E′F′,当D′E′恰好经过(1)中的点G时,请直接写出DD′的长度.
人教版
九年级数学上册
23.1
图形的旋转
培优训练-答案
一、选择题
1.
【答案】A [解析]
点P(-4,2)向右平移7个单位长度得到点P1(3,2),点P1绕原点逆时针旋转90°得到点P2(-2,3).故选A.
2.
【答案】D
3.
【答案】D [解析]
由旋转可得,S正方形ABCD=S四边形AECF=20,即AD2=20,∴AD=2
.
∵DE=2,∴在Rt△ADE中,AE==2
.故选D.
4.
【答案】D [解析]
由旋转的性质可知,AC=CD,但∠A不一定是60°,所以不能证明AC=AD,所以选项A错误;因为旋转角度不定,所以选项B不能确定;因为不确定AB和BC的数量关系,所以BC和DE的数量关系不能确定,所以选项C不能确定;由旋转的性质可知∠ACD=∠BCE,AC=DC,BC=EC,所以2∠A=180°-∠ACD,2∠EBC=180°-∠BCE,从而可证选项D是正确的.
5.
【答案】C [解析]
如图,连接BM.
∵△AEM与△ADM关于AM所在的直线对称,
∴AE=AD,∠MAD=∠MAE.
∵△ADM绕点A按顺时针方向旋转90°得到△ABF,
∴AF=AM,∠FAB=∠MAD,
∴∠FAB=∠MAE,
∴∠FAB+∠BAE=∠BAE+∠MAE,
即∠FAE=∠MAB,
∴△FAE≌△MAB(SAS),
∴EF=BM.
∵四边形ABCD是正方形,
∴BC=CD=AB=3.
∵DM=1,
∴CM=2.
∵在Rt△BCM中,BM==,
∴EF=.
6.
【答案】C [解析]
由题意可得∠CBD=α,∠C=∠EDB.
∵∠EDB+∠ADB=180°,
∴∠C+∠ADB=180°.
由四边形的内角和定理,得∠CAD+∠CBD=180°.
∴∠CAD=180°-∠CBD=180°-α.故选C.
7.
【答案】D
8.
【答案】B [解析]
连接PC.
在Rt△ABC中,∵∠A=30°,BC=2,
∴AB=4.
根据旋转的性质可知,∠A′CB′=90°,A′B′=AB=4.
∵P是A′B′的中点,∴PC=A′B′=2.
∵M是BC的中点,∴CM=BC=1.
又∵PM≤PC+CM,
即PM≤3,
∴PM的最大值为3(此时点P,C,M共线).
故选B.
二、填空题
9.
【答案】4 72
10.
【答案】将△OCD绕点C顺时针旋转90°,再向左平移2个单位长度即可得到△AOB(答案不唯一)
[解析]
观察图形可知,将△OCD绕点C顺时针旋转90°,再向左平移2个单位长度可得到△AOB(答案不唯一),注意是顺时针旋转还是逆时针旋转.
11.
【答案】+ [解析]
如图,连接CE′,
∵△ABC,△BDE都是等腰直角三角形,BA=BC,BD=BE,AC=4,DE=2
,
∴AB=BC=2
,BD=BE=2.
∵将△BDE绕点B逆时针旋转后得△BD′E′,
∴D′B=BE′=BD=2,∠D′BE′=90°,
∠D′BD=∠ABE′,
∴∠ABD′=∠CBE′,
∴△ABD′≌△CBE′(SAS),
∴∠D′=∠CE′B=45°.
过点B作BH⊥CE′于点H,
在Rt△BHE′中,BH=E′H=BE′=,
在Rt△BCH中,CH==,
∴CE′=+.故答案为+.
12.
【答案】(1,0)
13.
【答案】90 [解析]
连接AA1,CC1,分别作AA1和CC1的垂直平分线,两直线相交于点D,则点D即为旋转中心,连接AD,A1D,则∠ADA1=α=90°.
14.
【答案】15°或60° [解析]
分情况讨论:
①若DE⊥BC,设此时直线AD与BC交于点F,则∠BFA=90°-45°=45°,
∴∠BAD=180°-60°-45°=75°,∴α=90°-∠BAD=15°;
②若AD⊥BC,则∠BAD=30°,∴α=90°-∠BAD=60°.
故答案为15°或60°.
15.
【答案】(4,4)或(1,1)
[解析]
(1)若点A和点D、点B和点C分别为对应点,如图①,分别作线段AD,BC的垂直平分线,两条垂直平分线的交点P1(4,4)即为旋转中心;
(2)若点A和点C、点B和点D分别为对应点,如图②,分别作线段AC,BD的垂直平分线,两条垂直平分线的交点P2(1,1)即为旋转中心.综上所述,旋转中心的坐标是(4,4)或(1,1).
16.
【答案】 [解析]
∵==,==,
∴S1=S△AOB,S2=S△BOC.
∵点O是 ABCD的对称中心,
∴S△AOB=S△BOC=S平行四边形ABCD,∴=.
三、解答题
17.
【答案】
解:(1)证明:由题意可知,CD=CE,∠DCE=90°.
∵∠ACB=90°,
∴∠ACB-∠DCB=∠DCE-∠DCB,
即∠ACD=∠BCE.
在△ACD与△BCE中,
∴△ACD≌△BCE(SAS).
(2)∵∠ACB=90°,AC=BC,∴∠A=45°.
∵△ACD≌△BCE,
∴AD=BE,∠CBE=∠A=45°.
∵AD=BF,∴BE=BF,
∴∠BEF=×(180°-45°)=67.5°.
18.
【答案】
解:(1)∵将△ABD绕点A逆时针旋转,得到△ACD′,
∴∠DAD′=∠BAC.
∵∠BAC=90°,∴∠DAD′=90°.
(2)证明:∵△ABD绕点A逆时针旋转得到△ACD′,
∴AD=AD′,∠DAD′=∠BAC=90°.
∵∠DAE=45°,
∴∠D′AE=∠DAD′-∠DAE=90°-45°=45°,
∴∠D′AE=∠DAE.
在△AED与△AED′中,
∴△AED≌△AED′(SAS),
∴DE=D′E.
19.
【答案】
解:(1)证明:如图①,过点D作DE⊥CB交CB的延长线于点E,
∴∠BED=∠ACB=90°.
由旋转知,AB=BD,∠ABD=90°,
∴∠ABC+∠DBE=90°.
又∵∠A+∠ABC=90°,
∴∠A=∠DBE.
在△ABC和△BDE中,
∴△ABC≌△BDE(AAS),
∴BC=DE=a.
∵S△BCD=BC·DE,
∴S△BCD=a2.
(2)△BCD的面积为a2.
理由:如图②,过点D作CB的垂线,与CB的延长线交于点E,
∴∠BED=∠ACB=90°.
∵线段AB绕点B顺时针旋转90°得到线段BD,
∴AB=BD,∠ABD=90°,
∴∠ABC+∠DBE=90°.
又∵∠A+∠ABC=90°.
∴∠A=∠DBE.
在△ABC和△BDE中,
∴△ABC≌△BDE(AAS),
∴BC=DE=a.
∵S△BCD=BC·DE,∴S△BCD=a2.
(3)如图③,过点A作AF⊥BC于点F,过点D作DE⊥CB交CB的延长线于点E,
∴∠AFB=∠E=90°,BF=BC=a,
∴∠FAB+∠ABF=90°.
∵线段AB绕点B顺时针旋转90°得到线段BD,
∴∠ABD=90°,AB=BD,
∴∠ABF+∠DBE=90°,
∴∠FAB=∠DBE.
在△AFB和△BED中,
∴△AFB≌△BED(AAS),
∴BF=DE=a,
∴S△BCD=BC·DE=·a·a=a2.
20.
【答案】
解:(1)在Rt△ABC中,
∵∠B=60°,BC=2
,
∴AB=4,AC=6.
∵DF垂直平分AB,∴AD=2
.
又∵∠DAG=30°,
∴DG=2,AG=4,
∴GC=AC-AG=6-4=2.
(2)MD=ND.
证明:∵D是AB的中点,∠ACB=90°,
∴CD=DB=AD.
又∵∠B=60°,∴△CDB是等边三角形,
∴∠CDB=60°.
∵CN⊥DB,∴ND=DB.
∵∠EDF=90°,
∴∠EDA=180°-∠EDF-∠CDB=30°.
又∵∠A=30°,
∴∠A=∠EDA,∴HA=HD.
∵HM⊥AD,∴MD=AD.
又∵AD=DB,∴MD=ND.
(3)连接DG,则DG⊥AD′.
由(2)知∠A=∠EDA,
由平移知∠E′D′A=∠EDA,
∴∠A=∠E′D′A.
∵D′E′恰好经过(1)中的点G(此时点D′与点B重合),
∴D′G=AG,
∴DD′=AD=2
.
九年级数学上册
23.1
图形的旋转
培优训练
一、选择题
1.
在平面直角坐标系中,点P(-4,2)向右平移7个单位长度得到点P1,点P1绕原点逆时针旋转90°得到点P2,则点P2的坐标是( )
A.(-2,3)
B.(-3,2)
C.(2,-3)
D.(3,-2)
2.
观察图,其中可以看成是由“基本图案”通过旋转形成的共有( )
A.1个
B.2个
C.3个
D.4个
3.
如图,点E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置,若四边形AECF的面积为20,DE=2,则AE的长为( )
A.4
B.2
C.6
D.2
4.
如图,将△ABC绕点C顺时针旋转得到△DEC,使点A的对应点D恰好落在边AB上,点B的对应点为E,连接BE,下列结论一定正确的是( )
A.AC=AD
B.AB⊥EB
C.BC=DE
D.∠A=∠EBC
5.
2018·桂林
如图,在正方形ABCD中,AB=3,点M在边CD上,且DM=1,△AEM与△ADM关于AM所在的直线对称,将△ADM绕点A按顺时针方向旋转90°得到△ABF,连接EF,则线段EF的长为( )
A.3
B.2
C.
D.
6.
如图,将△ABC绕点B逆时针旋转α,得到△EBD,若点A恰好在ED的延长线上,则∠CAD的度数为( )
A.90°-α
B.α
C.180°-α
D.2α
7.
2019·河南
如图,在△OAB中,顶点O(0,0),A(-3,4),B(3,4),将△OAB与正方形ABCD组成的图形绕点O顺时针旋转,每次旋转90°,则第70次旋转结束时,点D的坐标为( )
A.(10,3)
B.(-3,10)
C.(10,-3)
D.(3,-10)
8.
如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A′B′C,M是BC的中点,P是A′B′的中点,连接PM.若BC=2,∠A=30°,则线段PM的最大值是( )
A.4
B.3
C.2
D.1
二、填空题
9.
如图,五角星的顶点是一个正五边形的五个顶点.这个五角星可以由一个基本图形(图中的阴影部分)绕中心点O至少经过______次旋转而得到,每一次旋转______度.
10.
如图,在平面直角坐标系xOy中,△AOB可以看作是由△OCD经过若干次图形的变化(平移、轴对称、旋转)得到的,写出一种由△OCD得到△AOB的过程:________________________________________________________________________________________________________________________________________________.
11.
如图,△ABC,△BDE都是等腰直角三角形,BA=BC,BD=BE,AC=4,DE=2
.将△BDE绕点B逆时针旋转后得△BD′E′,当点E′恰好落在线段AD′上时,CE′=________.
12.
如图所示,△ABC的顶点都在网格线的交点(格点)上,如果将△ABC绕点C逆时针旋转90°,那么点B的对应点B′的坐标是________.
13.
如图,在正方形网格中,格点△ABC绕某点顺时针旋转角α(0<α<180°)得到格点△A1B1C1,点A与点A1,点B与点B1,点C与点C1是对应点,则α=________°.
14.
一副三角尺如图放置,将三角尺ADE绕点A逆时针旋转α(0°<α<90°),使得三角尺ADE的一边所在的直线与BC垂直,则α的度数为________.
15.
分类讨论如图,点A的坐标为(-1,5),点B的坐标为(3,3),点C的坐标为(5,3),点D的坐标为(3,-1).小明发现线段AB与线段CD存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,你认为这个旋转中心的坐标是_________.
教师详解详析
16.
2018·陕西
如图,点O是平行四边形ABCD的对称中心,AD>AB,E,F是AB边上的点,且EF=AB;G,H是BC边上的点,且GH=BC.若S1,S2分别表示△EOF和△GOH的面积,则S1与S2之间的等量关系是=________.
三、解答题
17.
如图,在△ABC中,∠ACB=90°,AC=BC,D是AB边上一点(点D与点A,B不重合),连接CD,将线段CD绕点C逆时针旋转90°得到线段CE,连接DE交BC于点F,连接BE.
(1)求证:△ACD≌△BCE;
(2)当AD=BF时,求∠BEF的度数.
18.
如图,在△ABC中,∠BAC=90°,AB=AC,D,E是BC边上的点,将△ABD绕点A逆时针旋转得到△ACD′.
(1)求∠DAD′的度数;
(2)当∠DAE=45°时,求证:DE=D′E.
19.
请认真阅读下面的数学小探究系列,完成所提出的问题:
(1)探究1:如图①,在等腰直角三角形ABC中,∠ACB=90°,BC=a,将边AB绕点B顺时针旋转90°得到线段BD,连接CD.求证:△BCD的面积为a2.(提示:过点D作BC边上的高DE,可证△ABC≌△BDE)
(2)探究2:如图②,在一般的Rt△ABC中,∠ACB=90°,BC=a,将边AB绕点B顺时针旋转90°得到线段BD,连接CD,请用含a的式子表示△BCD的面积,并说明理由.
(3)探究3:如图③,在等腰三角形ABC中,AB=AC,BC=a,将边AB绕点B顺时针旋转90°得到线段BD,连接CD,试探究用含a的式子表示△BCD的面积,要有探究过程.
20.
将一副三角尺按图①摆放,等腰直角三角尺的直角边DF恰好垂直平分AB,与AC相交于点G,BC=2
.
(1)求GC的长;
(2)如图②,将△DEF绕点D顺时针旋转,使直角边DF经过点C,另一直角边DE与AC相交于点H,分别过点H,C作AB的垂线,垂足分别为M,N.通过观察,猜想MD与ND的数量关系,并验证你的猜想;
(3)在(2)的条件下,将△DEF沿DB方向平移得到△D′E′F′,当D′E′恰好经过(1)中的点G时,请直接写出DD′的长度.
人教版
九年级数学上册
23.1
图形的旋转
培优训练-答案
一、选择题
1.
【答案】A [解析]
点P(-4,2)向右平移7个单位长度得到点P1(3,2),点P1绕原点逆时针旋转90°得到点P2(-2,3).故选A.
2.
【答案】D
3.
【答案】D [解析]
由旋转可得,S正方形ABCD=S四边形AECF=20,即AD2=20,∴AD=2
.
∵DE=2,∴在Rt△ADE中,AE==2
.故选D.
4.
【答案】D [解析]
由旋转的性质可知,AC=CD,但∠A不一定是60°,所以不能证明AC=AD,所以选项A错误;因为旋转角度不定,所以选项B不能确定;因为不确定AB和BC的数量关系,所以BC和DE的数量关系不能确定,所以选项C不能确定;由旋转的性质可知∠ACD=∠BCE,AC=DC,BC=EC,所以2∠A=180°-∠ACD,2∠EBC=180°-∠BCE,从而可证选项D是正确的.
5.
【答案】C [解析]
如图,连接BM.
∵△AEM与△ADM关于AM所在的直线对称,
∴AE=AD,∠MAD=∠MAE.
∵△ADM绕点A按顺时针方向旋转90°得到△ABF,
∴AF=AM,∠FAB=∠MAD,
∴∠FAB=∠MAE,
∴∠FAB+∠BAE=∠BAE+∠MAE,
即∠FAE=∠MAB,
∴△FAE≌△MAB(SAS),
∴EF=BM.
∵四边形ABCD是正方形,
∴BC=CD=AB=3.
∵DM=1,
∴CM=2.
∵在Rt△BCM中,BM==,
∴EF=.
6.
【答案】C [解析]
由题意可得∠CBD=α,∠C=∠EDB.
∵∠EDB+∠ADB=180°,
∴∠C+∠ADB=180°.
由四边形的内角和定理,得∠CAD+∠CBD=180°.
∴∠CAD=180°-∠CBD=180°-α.故选C.
7.
【答案】D
8.
【答案】B [解析]
连接PC.
在Rt△ABC中,∵∠A=30°,BC=2,
∴AB=4.
根据旋转的性质可知,∠A′CB′=90°,A′B′=AB=4.
∵P是A′B′的中点,∴PC=A′B′=2.
∵M是BC的中点,∴CM=BC=1.
又∵PM≤PC+CM,
即PM≤3,
∴PM的最大值为3(此时点P,C,M共线).
故选B.
二、填空题
9.
【答案】4 72
10.
【答案】将△OCD绕点C顺时针旋转90°,再向左平移2个单位长度即可得到△AOB(答案不唯一)
[解析]
观察图形可知,将△OCD绕点C顺时针旋转90°,再向左平移2个单位长度可得到△AOB(答案不唯一),注意是顺时针旋转还是逆时针旋转.
11.
【答案】+ [解析]
如图,连接CE′,
∵△ABC,△BDE都是等腰直角三角形,BA=BC,BD=BE,AC=4,DE=2
,
∴AB=BC=2
,BD=BE=2.
∵将△BDE绕点B逆时针旋转后得△BD′E′,
∴D′B=BE′=BD=2,∠D′BE′=90°,
∠D′BD=∠ABE′,
∴∠ABD′=∠CBE′,
∴△ABD′≌△CBE′(SAS),
∴∠D′=∠CE′B=45°.
过点B作BH⊥CE′于点H,
在Rt△BHE′中,BH=E′H=BE′=,
在Rt△BCH中,CH==,
∴CE′=+.故答案为+.
12.
【答案】(1,0)
13.
【答案】90 [解析]
连接AA1,CC1,分别作AA1和CC1的垂直平分线,两直线相交于点D,则点D即为旋转中心,连接AD,A1D,则∠ADA1=α=90°.
14.
【答案】15°或60° [解析]
分情况讨论:
①若DE⊥BC,设此时直线AD与BC交于点F,则∠BFA=90°-45°=45°,
∴∠BAD=180°-60°-45°=75°,∴α=90°-∠BAD=15°;
②若AD⊥BC,则∠BAD=30°,∴α=90°-∠BAD=60°.
故答案为15°或60°.
15.
【答案】(4,4)或(1,1)
[解析]
(1)若点A和点D、点B和点C分别为对应点,如图①,分别作线段AD,BC的垂直平分线,两条垂直平分线的交点P1(4,4)即为旋转中心;
(2)若点A和点C、点B和点D分别为对应点,如图②,分别作线段AC,BD的垂直平分线,两条垂直平分线的交点P2(1,1)即为旋转中心.综上所述,旋转中心的坐标是(4,4)或(1,1).
16.
【答案】 [解析]
∵==,==,
∴S1=S△AOB,S2=S△BOC.
∵点O是 ABCD的对称中心,
∴S△AOB=S△BOC=S平行四边形ABCD,∴=.
三、解答题
17.
【答案】
解:(1)证明:由题意可知,CD=CE,∠DCE=90°.
∵∠ACB=90°,
∴∠ACB-∠DCB=∠DCE-∠DCB,
即∠ACD=∠BCE.
在△ACD与△BCE中,
∴△ACD≌△BCE(SAS).
(2)∵∠ACB=90°,AC=BC,∴∠A=45°.
∵△ACD≌△BCE,
∴AD=BE,∠CBE=∠A=45°.
∵AD=BF,∴BE=BF,
∴∠BEF=×(180°-45°)=67.5°.
18.
【答案】
解:(1)∵将△ABD绕点A逆时针旋转,得到△ACD′,
∴∠DAD′=∠BAC.
∵∠BAC=90°,∴∠DAD′=90°.
(2)证明:∵△ABD绕点A逆时针旋转得到△ACD′,
∴AD=AD′,∠DAD′=∠BAC=90°.
∵∠DAE=45°,
∴∠D′AE=∠DAD′-∠DAE=90°-45°=45°,
∴∠D′AE=∠DAE.
在△AED与△AED′中,
∴△AED≌△AED′(SAS),
∴DE=D′E.
19.
【答案】
解:(1)证明:如图①,过点D作DE⊥CB交CB的延长线于点E,
∴∠BED=∠ACB=90°.
由旋转知,AB=BD,∠ABD=90°,
∴∠ABC+∠DBE=90°.
又∵∠A+∠ABC=90°,
∴∠A=∠DBE.
在△ABC和△BDE中,
∴△ABC≌△BDE(AAS),
∴BC=DE=a.
∵S△BCD=BC·DE,
∴S△BCD=a2.
(2)△BCD的面积为a2.
理由:如图②,过点D作CB的垂线,与CB的延长线交于点E,
∴∠BED=∠ACB=90°.
∵线段AB绕点B顺时针旋转90°得到线段BD,
∴AB=BD,∠ABD=90°,
∴∠ABC+∠DBE=90°.
又∵∠A+∠ABC=90°.
∴∠A=∠DBE.
在△ABC和△BDE中,
∴△ABC≌△BDE(AAS),
∴BC=DE=a.
∵S△BCD=BC·DE,∴S△BCD=a2.
(3)如图③,过点A作AF⊥BC于点F,过点D作DE⊥CB交CB的延长线于点E,
∴∠AFB=∠E=90°,BF=BC=a,
∴∠FAB+∠ABF=90°.
∵线段AB绕点B顺时针旋转90°得到线段BD,
∴∠ABD=90°,AB=BD,
∴∠ABF+∠DBE=90°,
∴∠FAB=∠DBE.
在△AFB和△BED中,
∴△AFB≌△BED(AAS),
∴BF=DE=a,
∴S△BCD=BC·DE=·a·a=a2.
20.
【答案】
解:(1)在Rt△ABC中,
∵∠B=60°,BC=2
,
∴AB=4,AC=6.
∵DF垂直平分AB,∴AD=2
.
又∵∠DAG=30°,
∴DG=2,AG=4,
∴GC=AC-AG=6-4=2.
(2)MD=ND.
证明:∵D是AB的中点,∠ACB=90°,
∴CD=DB=AD.
又∵∠B=60°,∴△CDB是等边三角形,
∴∠CDB=60°.
∵CN⊥DB,∴ND=DB.
∵∠EDF=90°,
∴∠EDA=180°-∠EDF-∠CDB=30°.
又∵∠A=30°,
∴∠A=∠EDA,∴HA=HD.
∵HM⊥AD,∴MD=AD.
又∵AD=DB,∴MD=ND.
(3)连接DG,则DG⊥AD′.
由(2)知∠A=∠EDA,
由平移知∠E′D′A=∠EDA,
∴∠A=∠E′D′A.
∵D′E′恰好经过(1)中的点G(此时点D′与点B重合),
∴D′G=AG,
∴DD′=AD=2
.
同课章节目录
