24.3 正多边形和圆同步练习2021-2022学年九年级数学人教版上册(Word版 含答案)
文档属性
| 名称 | 24.3 正多边形和圆同步练习2021-2022学年九年级数学人教版上册(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 233.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-30 12:18:27 | ||
图片预览


文档简介
24.2.3
正多边形和圆同步练习
一、选择题
1.已知圆内接正三角形的边心距为1,则这个三角形的面积为( )
A.2
B.3
C.4
D.6
2.已知正三角形的边长为12,则这个正三角形外接圆的半径是( )
A.
B.
C.
D.
3.正六边形的边心距为,则该正六边形的边长是( )
A.
B.2
C.3
D.2
4.正三角形ABC内接于半径为2cm的圆,则AB所对弧的长为( )
A.
B.
C.
D.或
5.如图,P为正三角形ABC外接圆上一点,则∠APB=( )
A.150°
B.135°
C.115°
D.120°
6.已知圆的半径是2,则该圆的内接正六边形的面积是( )
A.3
B.9
C.18
D.36
7.如图,正六边形ABCDEF内接于⊙O,连接BD.则∠CBD的度数是( )
A.30°
B.45°
C.60°
D.90°
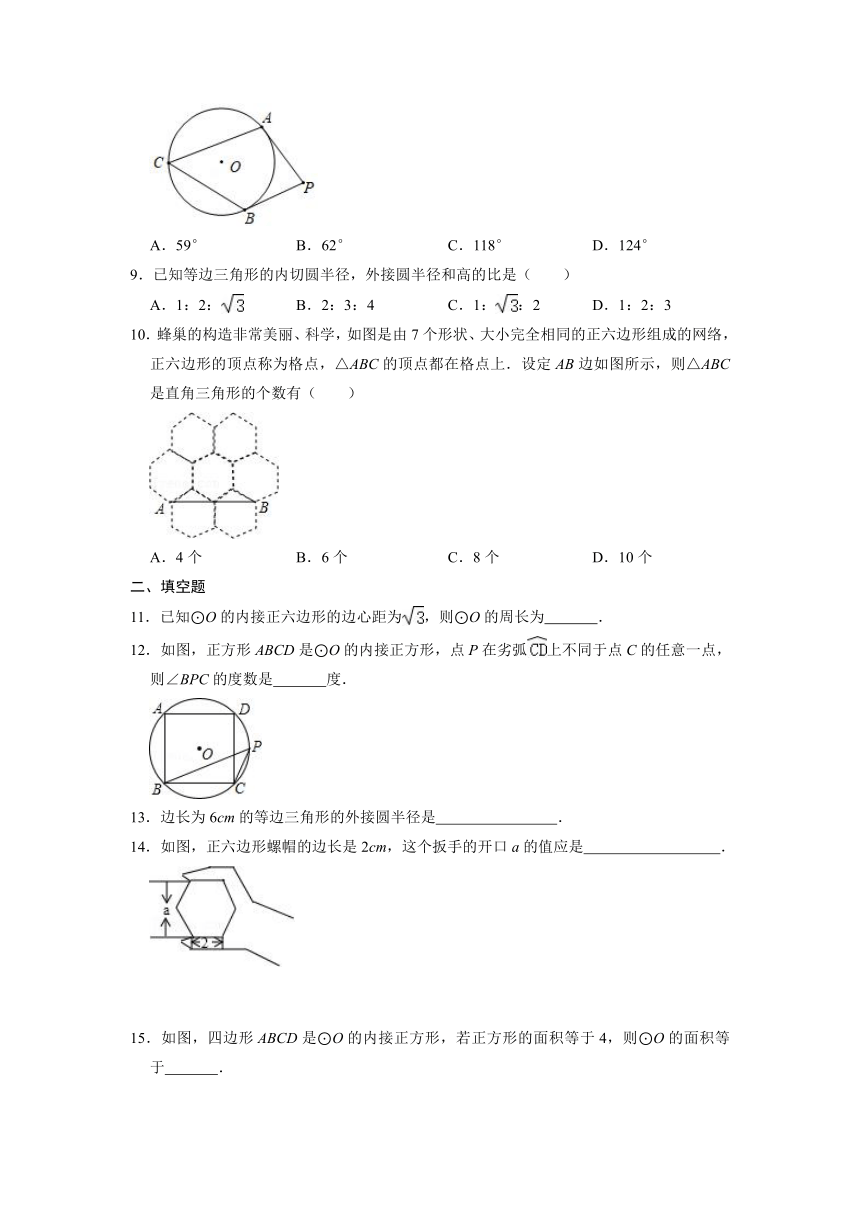
8.如图,PA、PB分别与⊙O相切于A、B两点,若∠C=59°,则∠P的度数为( )
A.59°
B.62°
C.118°
D.124°
9.已知等边三角形的内切圆半径,外接圆半径和高的比是( )
A.1:2:
B.2:3:4
C.1::2
D.1:2:3
10.蜂巢的构造非常美丽、科学,如图是由7个形状、大小完全相同的正六边形组成的网络,正六边形的顶点称为格点,△ABC的顶点都在格点上.设定AB边如图所示,则△ABC是直角三角形的个数有( )
A.4个
B.6个
C.8个
D.10个
二、填空题
11.已知⊙O的内接正六边形的边心距为,则⊙O的周长为
.
12.如图,正方形ABCD是⊙O的内接正方形,点P在劣弧上不同于点C的任意一点,则∠BPC的度数是
度.
13.边长为6cm的等边三角形的外接圆半径是
.
14.如图,正六边形螺帽的边长是2cm,这个扳手的开口a的值应是
.
15.如图,四边形ABCD是⊙O的内接正方形,若正方形的面积等于4,则⊙O的面积等于
.
16.如图,将正六边形ABCDEF放在直角坐标系中,中心与坐标原点重合,若A点的坐标为(﹣1,0),则点C的坐标为
.
三、解答题
17.如图,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.
(1)求证:△ABC是等边三角形.
(2)若⊙O的半径为2,求等边△ABC的边心距.
18.如图,正方形ABCD内接于⊙O,E是的中点,连接AE,DE,CE.
(1)求证:AE=DE;
(2)若CE=1,求四边形AECD的面积.
19.如图正方形ABCD内接于⊙O,E为CD任意一点,连接DE、AE.
(1)求∠AED的度数.
(2)如图2,过点B作BF∥DE交⊙O于点F,连接AF,AF=1,AE=4,求DE的长度.
24.2.3
正多边形和圆同步练习
1.已知圆内接正三角形的边心距为1,则这个三角形的面积为( )
A.2
B.3
C.4
D.6
【答案】B
【解答】解:如图所示:
作AD⊥BC与D,连接OB,
则AD经过圆心O,∠ODB=90°,OD=1,
∵△ABC是等边三角形,
∴BD=CD,∠OBD=∠ABC=30°,
∴OA=OB=2OD=2,
∴AD=3,BD=,
∴BC=2,
∴△ABC的面积=BC AD=×2×3=3;
故选:B.
2.已知正三角形的边长为12,则这个正三角形外接圆的半径是( )
A.
B.
C.
D.
【答案】C
【解答】解:如图所示,连接OB,作OD⊥BC,
∵BC=12,
∴BD=BC=6,
∵△ABC是等边三角形,
∴∠OBD=30°,
∴OB===4.
故选:C.
3.正六边形的边心距为,则该正六边形的边长是( )
A.
B.2
C.3
D.2
【答案】B
【解答】解:∵正六边形的边心距为,
∴OB=,AB=OA,
∵OA2=AB2+OB2,
∴OA2=(OA)2+()2,
解得OA=2.
故选:B.
4.正三角形ABC内接于半径为2cm的圆,则AB所对弧的长为( )
A.
B.
C.
D.或
【答案】D
【解答】解:因为三角形ABC是正三角形,所以AB所对的弧的度数为120°或240°.
当弧的度数为120°时,弧长为:=.
当弧的度数为240°时,弧长为:=.
故选:D.
5.如图,P为正三角形ABC外接圆上一点,则∠APB=( )
A.150°
B.135°
C.115°
D.120°
【答案】D
【解答】解:△ABC是正三角形,
∴∠ACB=60°,
∵∠APB+∠ACB=180°,
∴∠APB=120°.
故选:D.
6.已知圆的半径是2,则该圆的内接正六边形的面积是( )
A.3
B.9
C.18
D.36
【答案】C
【解答】解:连接OA、OB,作OG⊥AB于G,
∵等边三角形的边长是2,
∴高为3,
∴等边三角形的面积是3,
∴正六边形的面积是:18;
故选:C.
7.如图,正六边形ABCDEF内接于⊙O,连接BD.则∠CBD的度数是( )
A.30°
B.45°
C.60°
D.90°
【答案】A
【解答】解:∵在正六边形ABCDEF中,∠BCD==120°,BC=CD,
∴∠CBD=(180°﹣120°)=30°,
故选:A.
8.如图,PA、PB分别与⊙O相切于A、B两点,若∠C=59°,则∠P的度数为( )
A.59°
B.62°
C.118°
D.124°
【答案】B
【解答】解:连接OA、OB,如图所示:
∵PA、PB是⊙O切线,
∴PA⊥OA,PB⊥OB,
∴∠PAO=∠PBO=90°,
∵∠P+∠PAO+∠AOB+∠PBO=360°,
∴∠P=180°﹣∠AOB,
∵∠ACB=59°,
∴∠AOB=2∠ACB=118°,
∴∠P=180°﹣118°=62°,
故选:B.
9.已知等边三角形的内切圆半径,外接圆半径和高的比是( )
A.1:2:
B.2:3:4
C.1::2
D.1:2:3
【答案】D
【解答】解:图中内切圆半径是OD,外接圆的半径是OC,高是AD,
因而AD=OC+OD;
在直角△OCD中,∠DOC=60°,
则OD:OC=1:2,
因而OD:OC:AD=1:2:3,
所以内切圆半径,外接圆半径和高的比是1:2:3.故选:D.
10.蜂巢的构造非常美丽、科学,如图是由7个形状、大小完全相同的正六边形组成的网络,正六边形的顶点称为格点,△ABC的顶点都在格点上.设定AB边如图所示,则△ABC是直角三角形的个数有( )
A.4个
B.6个
C.8个
D.10个
【答案】D
【解答】解:如图,AB是直角边时,点C共有6个位置,
即,有6个直角三角形,
AB是斜边时,点C共有4个位置,
即有4个直角三角形,
综上所述,△ABC是直角三角形的个数有6+4=10个.
故选:D
已知⊙O的内接正六边形的边心距为,则⊙O的周长为
.
【答案】4Π
【解答】解:如图所示,连接OA、OB,
∵多边形ABCDEF是正六边形,
∴∠AOB=60°,
∵OA=OB,
∴△AOB是等边三角形,
∴∠OAM=60°,
∴OM=OA sin∠OAM,
∴OA===2,
∴⊙O的周长为4π,
故答案为:4π.
12.如图,正方形ABCD是⊙O的内接正方形,点P在劣弧上不同于点C的任意一点,则∠BPC的度数是
度.
【答案】45
【解答】解:连接OB,OC,如图所示:
∵四边形ABCD为正方形,∴∠BOC=90°,
∴∠P=∠BOC=45°.
故答案为:45.
13.边长为6cm的等边三角形的外接圆半径是
.
【答案】2
【解答】解:连接中心和顶点,作出边心距.
那么得到直角三角形在中心的度数为:360÷3÷2=60°,那么外接圆半径是6÷2÷sin60°=2;
故答案为:2.
14.如图,正六边形螺帽的边长是2cm,这个扳手的开口a的值应是
.
【答案】2cm.
【解答】解:过正六边形的中心作边的垂线,连接OA.
则∠O=30°,AB=1
∴OB==cm.
∴a=2OB=2cm.
故答案是:2cm.
15.如图,四边形ABCD是⊙O的内接正方形,若正方形的面积等于4,则⊙O的面积等于
.
【答案】2Π
【解答】解:正方形的边长AB=2,
则半径是2×=,
则面积是()2π=2π.
故答案是:2π.
16.如图,将正六边形ABCDEF放在直角坐标系中,中心与坐标原点重合,若A点的坐标为(﹣1,0),则点C的坐标为
.
【答案】(,﹣)
【解答】解:连接OE,由正六边形是轴对称图形知:
在Rt△OEG中,∠GOE=30°,OE=1.
∴GE=,OG=.
∴A(﹣1,0),B(﹣,﹣),C(,﹣)D(1,0),E(,),F(﹣,).
故答案为:(,﹣)
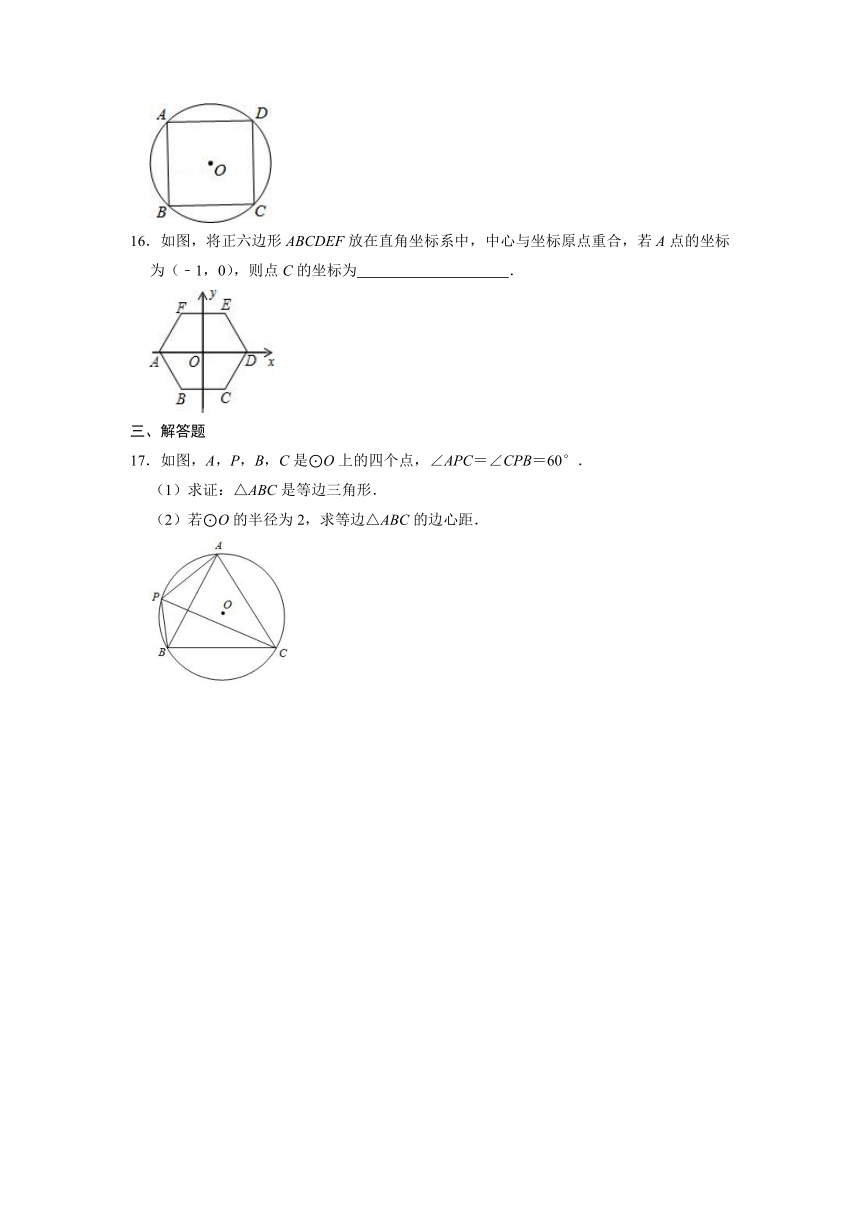
17.如图,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.
(1)求证:△ABC是等边三角形.
(2)若⊙O的半径为2,求等边△ABC的边心距.
【答案】(1)略
(2)等边△ABC的边心距为1
(3)
【解答】(1)证明:在⊙O中,
∵∠BAC与∠CPB是对的圆周角,∠ABC与∠APC是所对的圆周角,
∴∠BAC=∠CPB,∠ABC=∠APC,
又∵∠APC=∠CPB=60°,
∴∠ABC=∠BAC=60°,
∴△ABC为等边三角形;
(2)过O作OD⊥BC于D,连接OB,
则∠OBD=30°,∠ODB=90°,
∵OB=2,
∴OD=1,
∴等边△ABC的边心距为1.
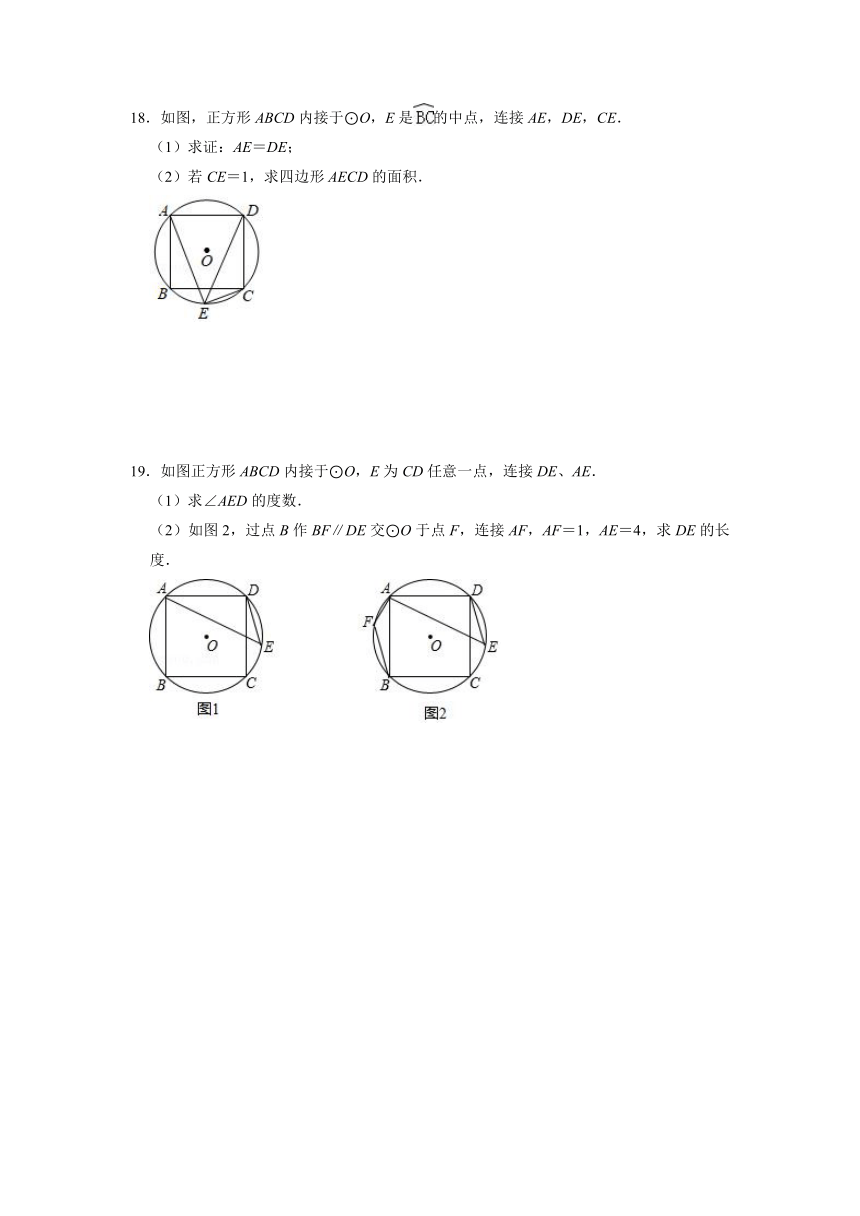
18.如图,正方形ABCD内接于⊙O,E是的中点,连接AE,DE,CE.
(1)求证:AE=DE;
(2)若CE=1,求四边形AECD的面积.
【答案】(1)略
(2)S△DEF=+
【解答】(1)证明:∵四边形ABCD是正方形,
∴AB=CD,
∴=,
∵E是的中点,
∴=,
∴=,
∴AE=DE.
(2)解:连接BD,过点D作DF⊥DE交EC的延长线于F.
∵四边形ABCD是正方形,
∴∠DBC=∠DEC=45°,DA=DC,
∵∠EDF=90°,
∴∠F=90°﹣45°=45°,
∴DE=DF,
∵∠ADC=∠EDF=90°,
∴∠ADE=∠CDF,
在△ADE和△CDF中,
,
∴△ADE≌△CDF(AAS),
∴AE=CF,
∴S△ADE=S△CDF,
∴S四边形AECD=S△DEF,
∵EF=DE=EC+DE,EC=1,
∴1+DE=DE,
∴DE=+1,
∴S△DEF=DE2=+.
19.如图正方形ABCD内接于⊙O,E为CD任意一点,连接DE、AE.
(1)求∠AED的度数.
(2)如图2,过点B作BF∥DE交⊙O于点F,连接AF,AF=1,AE=4,求DE的长度.
【答案】(1)∠AED=45°
(2)DE=
【解答】解:(1)如图1中,连接OA、OD.
∵四边形ABCD是正方形,
∴∠AOD=90°,
∴∠AED=∠AOD=45°.
(2)如图2中,连接CF,CE,CA,BD,作DH⊥AE于H.
∵BF∥DE,AB∥CD,
∴∠BDE=∠DBF,∠BDC=∠ABD,
∴∠ABF=∠CDE,
∵∠CFA=∠AEC=90°,
∴∠DEC=∠AFB=135°,
∵CD=AB,
∴△CDE≌△ABF,
∴AF=CE=1,
∴AC==,
∴AD=AC=,
∵∠DHE=90°,
∴∠HDE=∠HED=45°,
∴DH=HE,设DH=EH=x,
在Rt△ADH中,∵AD2=AH2+DH2,
∴=(4﹣x)2+x2,
解得x=或(舍弃),
∴DE=DH=
正多边形和圆同步练习
一、选择题
1.已知圆内接正三角形的边心距为1,则这个三角形的面积为( )
A.2
B.3
C.4
D.6
2.已知正三角形的边长为12,则这个正三角形外接圆的半径是( )
A.
B.
C.
D.
3.正六边形的边心距为,则该正六边形的边长是( )
A.
B.2
C.3
D.2
4.正三角形ABC内接于半径为2cm的圆,则AB所对弧的长为( )
A.
B.
C.
D.或
5.如图,P为正三角形ABC外接圆上一点,则∠APB=( )
A.150°
B.135°
C.115°
D.120°
6.已知圆的半径是2,则该圆的内接正六边形的面积是( )
A.3
B.9
C.18
D.36
7.如图,正六边形ABCDEF内接于⊙O,连接BD.则∠CBD的度数是( )
A.30°
B.45°
C.60°
D.90°
8.如图,PA、PB分别与⊙O相切于A、B两点,若∠C=59°,则∠P的度数为( )
A.59°
B.62°
C.118°
D.124°
9.已知等边三角形的内切圆半径,外接圆半径和高的比是( )
A.1:2:
B.2:3:4
C.1::2
D.1:2:3
10.蜂巢的构造非常美丽、科学,如图是由7个形状、大小完全相同的正六边形组成的网络,正六边形的顶点称为格点,△ABC的顶点都在格点上.设定AB边如图所示,则△ABC是直角三角形的个数有( )
A.4个
B.6个
C.8个
D.10个
二、填空题
11.已知⊙O的内接正六边形的边心距为,则⊙O的周长为
.
12.如图,正方形ABCD是⊙O的内接正方形,点P在劣弧上不同于点C的任意一点,则∠BPC的度数是
度.
13.边长为6cm的等边三角形的外接圆半径是
.
14.如图,正六边形螺帽的边长是2cm,这个扳手的开口a的值应是
.
15.如图,四边形ABCD是⊙O的内接正方形,若正方形的面积等于4,则⊙O的面积等于
.
16.如图,将正六边形ABCDEF放在直角坐标系中,中心与坐标原点重合,若A点的坐标为(﹣1,0),则点C的坐标为
.
三、解答题
17.如图,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.
(1)求证:△ABC是等边三角形.
(2)若⊙O的半径为2,求等边△ABC的边心距.
18.如图,正方形ABCD内接于⊙O,E是的中点,连接AE,DE,CE.
(1)求证:AE=DE;
(2)若CE=1,求四边形AECD的面积.
19.如图正方形ABCD内接于⊙O,E为CD任意一点,连接DE、AE.
(1)求∠AED的度数.
(2)如图2,过点B作BF∥DE交⊙O于点F,连接AF,AF=1,AE=4,求DE的长度.
24.2.3
正多边形和圆同步练习
1.已知圆内接正三角形的边心距为1,则这个三角形的面积为( )
A.2
B.3
C.4
D.6
【答案】B
【解答】解:如图所示:
作AD⊥BC与D,连接OB,
则AD经过圆心O,∠ODB=90°,OD=1,
∵△ABC是等边三角形,
∴BD=CD,∠OBD=∠ABC=30°,
∴OA=OB=2OD=2,
∴AD=3,BD=,
∴BC=2,
∴△ABC的面积=BC AD=×2×3=3;
故选:B.
2.已知正三角形的边长为12,则这个正三角形外接圆的半径是( )
A.
B.
C.
D.
【答案】C
【解答】解:如图所示,连接OB,作OD⊥BC,
∵BC=12,
∴BD=BC=6,
∵△ABC是等边三角形,
∴∠OBD=30°,
∴OB===4.
故选:C.
3.正六边形的边心距为,则该正六边形的边长是( )
A.
B.2
C.3
D.2
【答案】B
【解答】解:∵正六边形的边心距为,
∴OB=,AB=OA,
∵OA2=AB2+OB2,
∴OA2=(OA)2+()2,
解得OA=2.
故选:B.
4.正三角形ABC内接于半径为2cm的圆,则AB所对弧的长为( )
A.
B.
C.
D.或
【答案】D
【解答】解:因为三角形ABC是正三角形,所以AB所对的弧的度数为120°或240°.
当弧的度数为120°时,弧长为:=.
当弧的度数为240°时,弧长为:=.
故选:D.
5.如图,P为正三角形ABC外接圆上一点,则∠APB=( )
A.150°
B.135°
C.115°
D.120°
【答案】D
【解答】解:△ABC是正三角形,
∴∠ACB=60°,
∵∠APB+∠ACB=180°,
∴∠APB=120°.
故选:D.
6.已知圆的半径是2,则该圆的内接正六边形的面积是( )
A.3
B.9
C.18
D.36
【答案】C
【解答】解:连接OA、OB,作OG⊥AB于G,
∵等边三角形的边长是2,
∴高为3,
∴等边三角形的面积是3,
∴正六边形的面积是:18;
故选:C.
7.如图,正六边形ABCDEF内接于⊙O,连接BD.则∠CBD的度数是( )
A.30°
B.45°
C.60°
D.90°
【答案】A
【解答】解:∵在正六边形ABCDEF中,∠BCD==120°,BC=CD,
∴∠CBD=(180°﹣120°)=30°,
故选:A.
8.如图,PA、PB分别与⊙O相切于A、B两点,若∠C=59°,则∠P的度数为( )
A.59°
B.62°
C.118°
D.124°
【答案】B
【解答】解:连接OA、OB,如图所示:
∵PA、PB是⊙O切线,
∴PA⊥OA,PB⊥OB,
∴∠PAO=∠PBO=90°,
∵∠P+∠PAO+∠AOB+∠PBO=360°,
∴∠P=180°﹣∠AOB,
∵∠ACB=59°,
∴∠AOB=2∠ACB=118°,
∴∠P=180°﹣118°=62°,
故选:B.
9.已知等边三角形的内切圆半径,外接圆半径和高的比是( )
A.1:2:
B.2:3:4
C.1::2
D.1:2:3
【答案】D
【解答】解:图中内切圆半径是OD,外接圆的半径是OC,高是AD,
因而AD=OC+OD;
在直角△OCD中,∠DOC=60°,
则OD:OC=1:2,
因而OD:OC:AD=1:2:3,
所以内切圆半径,外接圆半径和高的比是1:2:3.故选:D.
10.蜂巢的构造非常美丽、科学,如图是由7个形状、大小完全相同的正六边形组成的网络,正六边形的顶点称为格点,△ABC的顶点都在格点上.设定AB边如图所示,则△ABC是直角三角形的个数有( )
A.4个
B.6个
C.8个
D.10个
【答案】D
【解答】解:如图,AB是直角边时,点C共有6个位置,
即,有6个直角三角形,
AB是斜边时,点C共有4个位置,
即有4个直角三角形,
综上所述,△ABC是直角三角形的个数有6+4=10个.
故选:D
已知⊙O的内接正六边形的边心距为,则⊙O的周长为
.
【答案】4Π
【解答】解:如图所示,连接OA、OB,
∵多边形ABCDEF是正六边形,
∴∠AOB=60°,
∵OA=OB,
∴△AOB是等边三角形,
∴∠OAM=60°,
∴OM=OA sin∠OAM,
∴OA===2,
∴⊙O的周长为4π,
故答案为:4π.
12.如图,正方形ABCD是⊙O的内接正方形,点P在劣弧上不同于点C的任意一点,则∠BPC的度数是
度.
【答案】45
【解答】解:连接OB,OC,如图所示:
∵四边形ABCD为正方形,∴∠BOC=90°,
∴∠P=∠BOC=45°.
故答案为:45.
13.边长为6cm的等边三角形的外接圆半径是
.
【答案】2
【解答】解:连接中心和顶点,作出边心距.
那么得到直角三角形在中心的度数为:360÷3÷2=60°,那么外接圆半径是6÷2÷sin60°=2;
故答案为:2.
14.如图,正六边形螺帽的边长是2cm,这个扳手的开口a的值应是
.
【答案】2cm.
【解答】解:过正六边形的中心作边的垂线,连接OA.
则∠O=30°,AB=1
∴OB==cm.
∴a=2OB=2cm.
故答案是:2cm.
15.如图,四边形ABCD是⊙O的内接正方形,若正方形的面积等于4,则⊙O的面积等于
.
【答案】2Π
【解答】解:正方形的边长AB=2,
则半径是2×=,
则面积是()2π=2π.
故答案是:2π.
16.如图,将正六边形ABCDEF放在直角坐标系中,中心与坐标原点重合,若A点的坐标为(﹣1,0),则点C的坐标为
.
【答案】(,﹣)
【解答】解:连接OE,由正六边形是轴对称图形知:
在Rt△OEG中,∠GOE=30°,OE=1.
∴GE=,OG=.
∴A(﹣1,0),B(﹣,﹣),C(,﹣)D(1,0),E(,),F(﹣,).
故答案为:(,﹣)
17.如图,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.
(1)求证:△ABC是等边三角形.
(2)若⊙O的半径为2,求等边△ABC的边心距.
【答案】(1)略
(2)等边△ABC的边心距为1
(3)
【解答】(1)证明:在⊙O中,
∵∠BAC与∠CPB是对的圆周角,∠ABC与∠APC是所对的圆周角,
∴∠BAC=∠CPB,∠ABC=∠APC,
又∵∠APC=∠CPB=60°,
∴∠ABC=∠BAC=60°,
∴△ABC为等边三角形;
(2)过O作OD⊥BC于D,连接OB,
则∠OBD=30°,∠ODB=90°,
∵OB=2,
∴OD=1,
∴等边△ABC的边心距为1.
18.如图,正方形ABCD内接于⊙O,E是的中点,连接AE,DE,CE.
(1)求证:AE=DE;
(2)若CE=1,求四边形AECD的面积.
【答案】(1)略
(2)S△DEF=+
【解答】(1)证明:∵四边形ABCD是正方形,
∴AB=CD,
∴=,
∵E是的中点,
∴=,
∴=,
∴AE=DE.
(2)解:连接BD,过点D作DF⊥DE交EC的延长线于F.
∵四边形ABCD是正方形,
∴∠DBC=∠DEC=45°,DA=DC,
∵∠EDF=90°,
∴∠F=90°﹣45°=45°,
∴DE=DF,
∵∠ADC=∠EDF=90°,
∴∠ADE=∠CDF,
在△ADE和△CDF中,
,
∴△ADE≌△CDF(AAS),
∴AE=CF,
∴S△ADE=S△CDF,
∴S四边形AECD=S△DEF,
∵EF=DE=EC+DE,EC=1,
∴1+DE=DE,
∴DE=+1,
∴S△DEF=DE2=+.
19.如图正方形ABCD内接于⊙O,E为CD任意一点,连接DE、AE.
(1)求∠AED的度数.
(2)如图2,过点B作BF∥DE交⊙O于点F,连接AF,AF=1,AE=4,求DE的长度.
【答案】(1)∠AED=45°
(2)DE=
【解答】解:(1)如图1中,连接OA、OD.
∵四边形ABCD是正方形,
∴∠AOD=90°,
∴∠AED=∠AOD=45°.
(2)如图2中,连接CF,CE,CA,BD,作DH⊥AE于H.
∵BF∥DE,AB∥CD,
∴∠BDE=∠DBF,∠BDC=∠ABD,
∴∠ABF=∠CDE,
∵∠CFA=∠AEC=90°,
∴∠DEC=∠AFB=135°,
∵CD=AB,
∴△CDE≌△ABF,
∴AF=CE=1,
∴AC==,
∴AD=AC=,
∵∠DHE=90°,
∴∠HDE=∠HED=45°,
∴DH=HE,设DH=EH=x,
在Rt△ADH中,∵AD2=AH2+DH2,
∴=(4﹣x)2+x2,
解得x=或(舍弃),
∴DE=DH=
同课章节目录
