12.1 全等三角形巩固练习2020-2021学年人教版八年级上册数学(Word版 含答案)
文档属性
| 名称 | 12.1 全等三角形巩固练习2020-2021学年人教版八年级上册数学(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 120.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-30 12:22:11 | ||
图片预览


文档简介
12.1
全等三角形巩固练习
【巩固练习】
一、选择题
1.
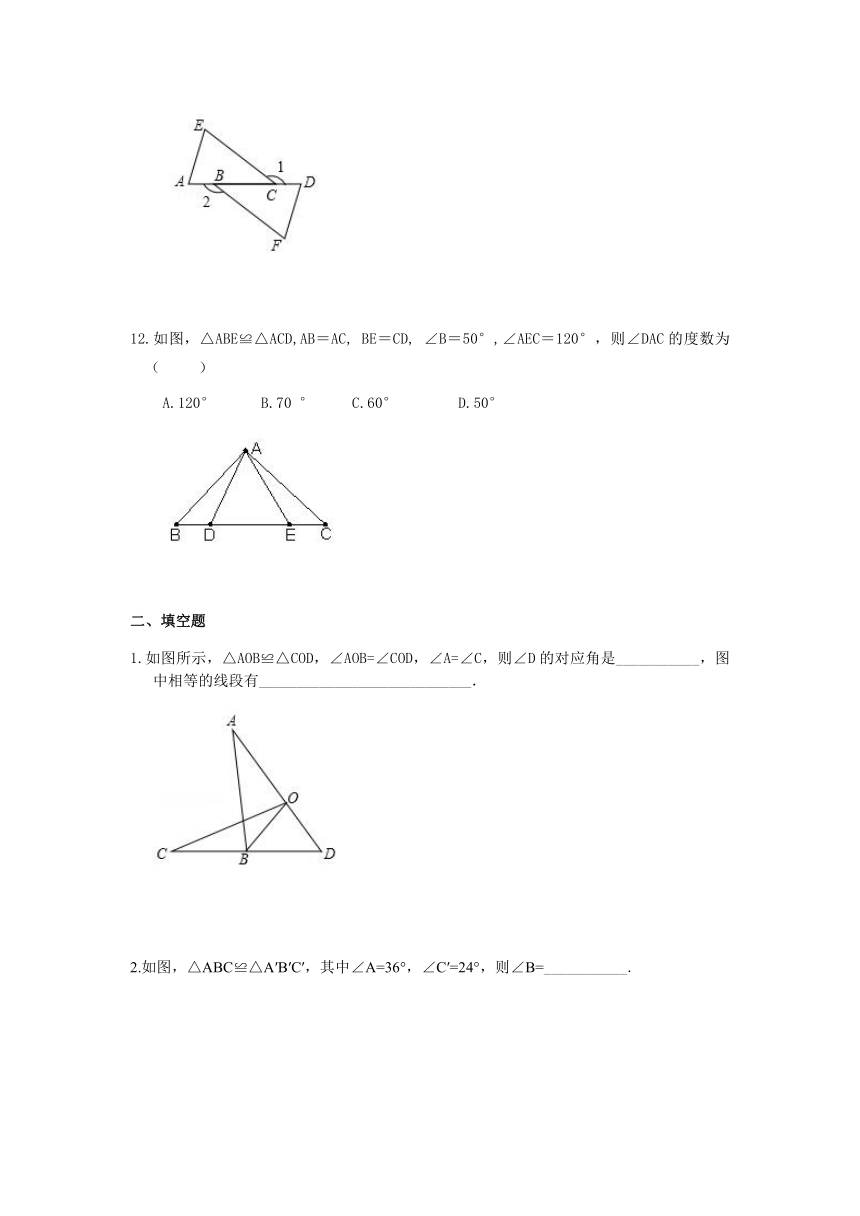
如图所示,△ABC≌△DEC,则不能得到的结论是(
)
A.
AB=DE
B.
∠A=∠D
C.
BC=CD
D.
∠ACD=∠BCE
2.
如图,△ABC≌△BAD,A和B,C和D分别是对应顶点,若AB=6,AC=4,BC=5,则AD的长为(
)
A.
4
B.
5
C.
6
D.
以上都不对
3.
下列说法中正确的有(
)
①形状相同的两个图形是全等图形
②对应角相等的两个三角形是全等三角形
③全等三角形的面积相等
④若△ABC≌△DEF,△DEF
≌△MNP,△ABC≌△MNP.
A.0个
B.1个
C.2个
D.3个
4.
如图,△ABC≌△A′B′C,∠ACB=90°,∠A′CB=20°,则∠BCB′的度数为( )
A.20°
B.40°
C.70°
D.90°
5.
已知△ABC≌△DEF,BC=EF=6cm,△ABC的面积为18平方厘米,则EF边上的高是(
)
A.6cm
B.7cm
C.8cm
D.9cm
6.
将一张长方形纸片按如图所示的方式折叠,BC、BD分别为折痕,则∠CBD的度数为( )
A.60°
B.75° C.90°
D.95°
7.下列命题中,真命题的个数是
(
)
①全等三角形的周长相等
②全等三角形的对应角相等
③全等三角形的面积相等
④面积相等的两个三角形全等
A.4个
B.3个
C.2个
D.1个
8.如图,△ABC≌△ADE,若∠B=80°,∠C=30°,∠DAB:∠DAC=4:3,则∠EFC的度数为( )
A.30°
B.40°
C.70°
D.80°
9.下列命题中:⑴形状相同的两个三角形是全等形;⑵在两个三角形中,相等的角是对应角,相等的边是对应边;⑶全等三角形对应边上的高、中线及对应角平分线分别相等,其中真命题的个数有(
)
A.3个
B.2个
C.1个
D.0个
10.△ABC≌△DEF,且△ABC的周长为100,A、B分别与D、E对应,且AB=35,DF=30,则EF的长为( )
A.35
B.30
C.45
D.55
11.如图,已知△ACE≌△DFB,下列结论中正确的个数是( )
①AC=DB;②AB=DC;③∠1=∠2;④AE∥DF;⑤S△ACE=S△DFB;⑥BC=AE;⑦BF∥EC.
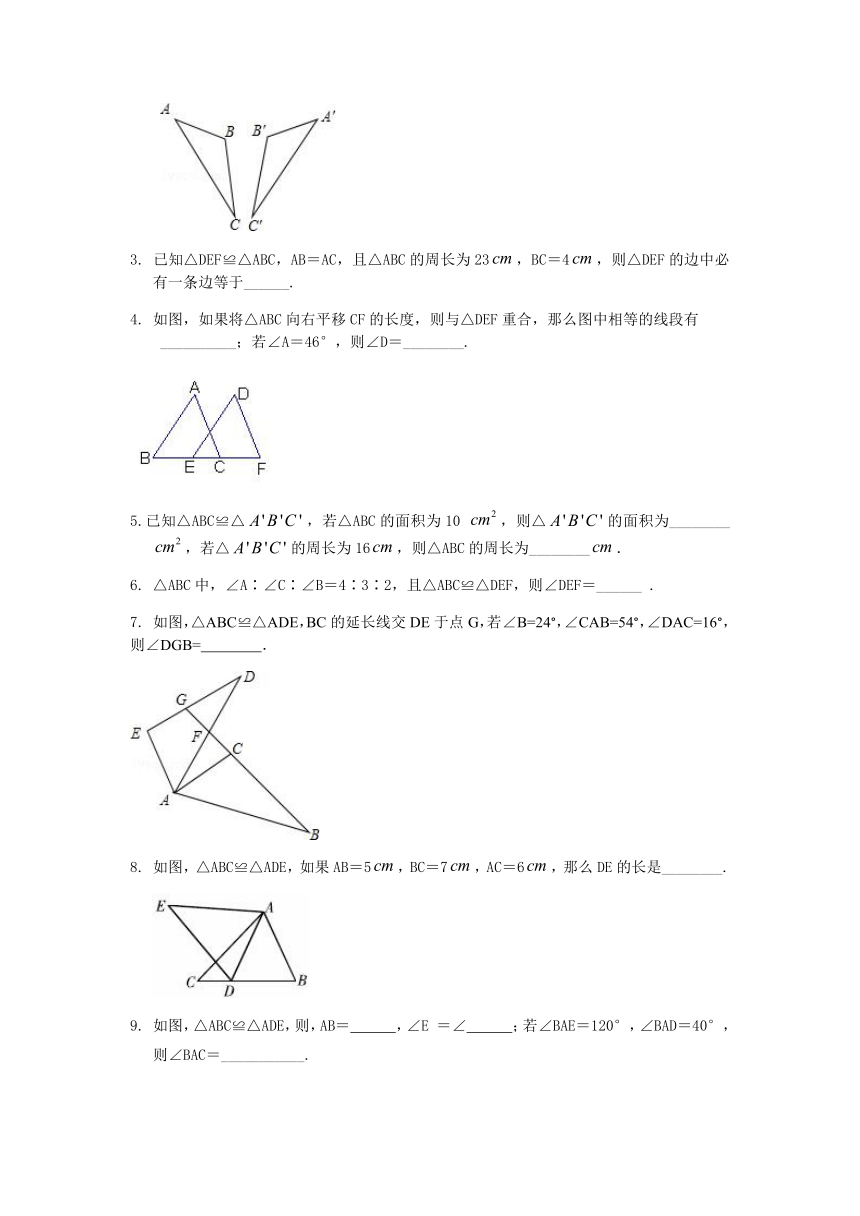
12.如图,△ABE≌△ACD,AB=AC,
BE=CD,
∠B=50°,∠AEC=120°,则∠DAC的度数为
(
)
A.120°
B.70
°
C.60°
D.50°
二、填空题
1.如图所示,△AOB≌△COD,∠AOB=∠COD,∠A=∠C,则∠D的对应角是___________,图中相等的线段有____________________________.
2.如图,△ABC≌△A′B′C′,其中∠A=36°,∠C′=24°,则∠B=___________.
3.
已知△DEF≌△ABC,AB=AC,且△ABC的周长为23,BC=4,则△DEF的边中必有一条边等于______.
4.
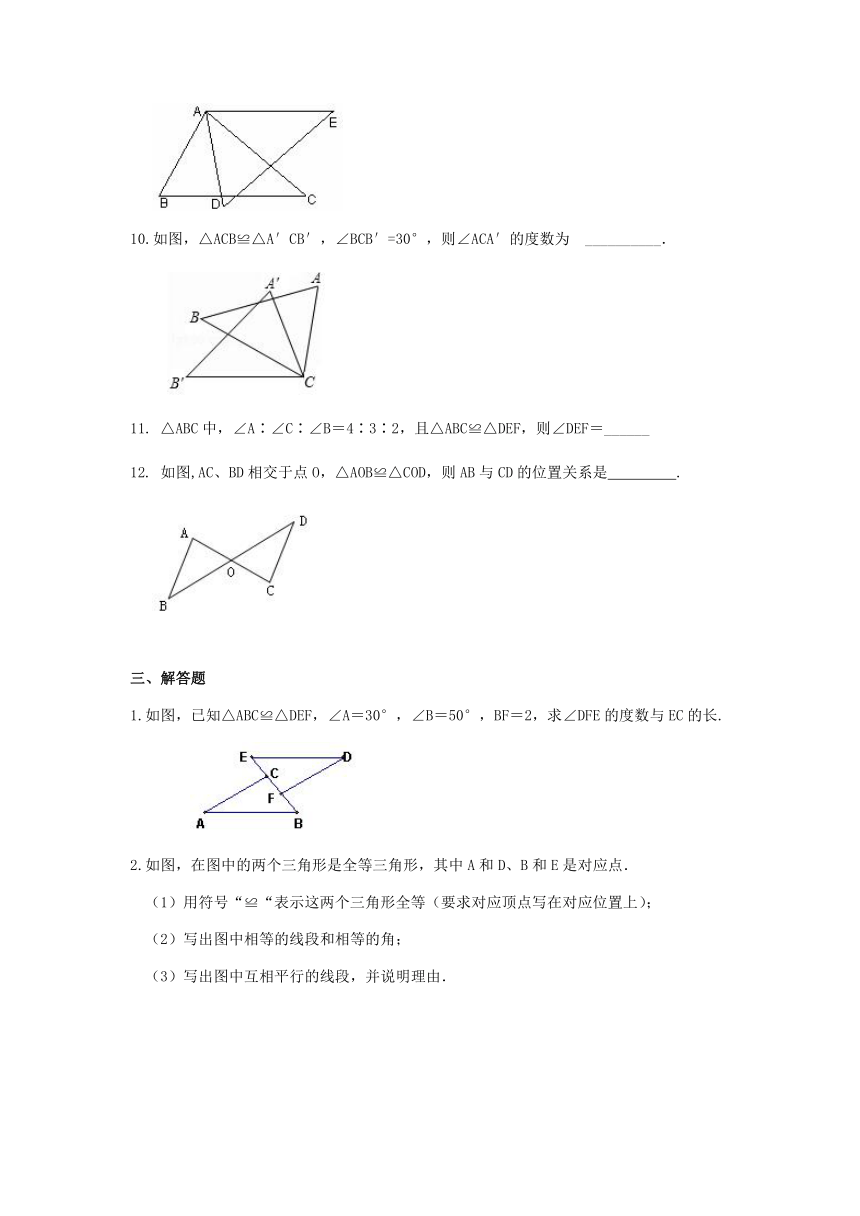
如图,如果将△ABC向右平移CF的长度,则与△DEF重合,那么图中相等的线段有__________;若∠A=46°,则∠D=________.
5.已知△ABC≌△,若△ABC的面积为10
,则△的面积为________
,若△的周长为16,则△ABC的周长为________.
6.
△ABC中,∠A∶∠C∶∠B=4∶3∶2,且△ABC≌△DEF,则∠DEF=______
.
7.
如图,△ABC≌△ADE,BC的延长线交DE于点G,若∠B=24°,∠CAB=54°,∠DAC=16°,则∠DGB=
.
8.
如图,△ABC≌△ADE,如果AB=5,BC=7,AC=6,那么DE的长是________.
9.
如图,△ABC≌△ADE,则,AB=
,∠E
=∠
;若∠BAE=120°,∠BAD=40°,则∠BAC=___________.
10.如图,△ACB≌△A′CB′,∠BCB′=30°,则∠ACA′的度数为 __________.
11.
△ABC中,∠A∶∠C∶∠B=4∶3∶2,且△ABC≌△DEF,则∠DEF=______
12.
如图,AC、BD相交于点O,△AOB≌△COD,则AB与CD的位置关系是
.
三、解答题
1.如图,已知△ABC≌△DEF,∠A=30°,∠B=50°,BF=2,求∠DFE的度数与EC的长.
2.如图,在图中的两个三角形是全等三角形,其中A和D、B和E是对应点.
(1)用符号“≌“表示这两个三角形全等(要求对应顶点写在对应位置上);
(2)写出图中相等的线段和相等的角;
(3)写出图中互相平行的线段,并说明理由.
3.
如图,E为线段BC上一点,AB⊥BC,△ABE≌△ECD.判断AE与DE的关系,并证明你的结论.
4.
如图,△ABC中,∠ACB=90°,△ABC≌△DFC,你能判断DE与AB互相垂直吗?说出你的理由.
5.如图,已知△ABC≌△DEF,∠A=30°,∠B=50°,BF=2,求∠DFE的度数和EC的长.
6.如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,
(1)写出图中一对全等的三角形,并写出它们的所有对应角;
(2)设的度数为,∠的度数为,那么∠1,∠2的度数分别是多少?(用含有或的代数式表示)
(3)∠A与∠1+∠2之间有一种数量关系始终保持不变,请找出这个规律.
【答案与解析】
一.选择题
1.
【答案】C;
【解析】因为△ABC≌△DEC,可得:AB=DE,∠A=∠D,BC=EC,∠ACD=∠BCE,
故选C.
2.
【答案】B;
【解析】AD与BC是对应边,全等三角形对应边相等.
3.
【答案】C;
【解析】③和④是正确的;
4.
【答案】C;
【解析】解:∵△ACB≌△A′CB′,
∴∠ACB=∠A′CB′,
∴∠BCB′=∠A′CB′﹣∠A′CB=70°.
故选C.
5.
【答案】A;
【解析】EF边上的高=;
6.
【答案】C;
【解析】折叠所成的两个三角形全等,找到对应角可解.
7.
【答案】
B;
【解析】①②③是正确的;
8.
【答案】C;
【解析】∵∠B=80°,∠C=30°,∴∠BAC=180°﹣∠B﹣∠C=70°,∵△ABC≌△ADE,
∴∠DAE=∠BAC=70°,∠E=∠C=30°.∵∠DAB:∠DAC=4:3,∴∠DAB=40°,∠DAC=30°,
∴∠EAC=∠DAE﹣∠DAC=70°﹣30°=40°,∴∠EFC=∠E+∠EAC=30°+40°=70°.
9.
【答案】C;
【解析】只有(3)是正确的命题;
10.
【答案】A;
【解析】AC=DF=30,EF=BC=100-35-30=35;
11.
【答案】C;
【解析】解:∵△ACE≌△DFB,
∴AC=DB,①正确;
∠ECA=∠DBF,∠A=∠D,S△ACE=S△DFB,⑤正确;
∵AB+BC=CD+BC,
∴AB=CD
②正确;
∵∠ECA=∠DBF,
∴BF∥EC,⑦正确;
∠1=∠2,③正确;
∵∠A=∠D,
∴AE∥DF,④正确.
BC与AE,不是对应边,也没有办法证明二者相等,⑥不正确.
故选C.
12.
【答案】B;
【解析】由全等三角形的性质,易得∠BAD=∠CAE=10°,∠BAC=80°,所以∠DAC=70°.
二.填空题
1.
【答案】∠OBA,OA=OC、OB=OD、AB=CD;
【解析】解:∵△AOB≌△COD,∠AOB=∠COD,∠A=∠C,
∴∠D=∠OBA,OA=OC、OB=OD、AB=CD,
故答案为:∠OBA,OA=OC、OB=OD、AB=CD.
2.
【答案】120°;
【解析】∵△ABC≌△A′B′C′,∴∠C=∠C′=24°,∴∠B=180°﹣∠A﹣∠B=120°.
3.
【答案】4或9.5;
【解析】DE=DF=9.5,EF=4;
4.【答案】AB=DE、AC=DF、BC=EF、BE=CF,
46°;
5.【答案】10,16;
【解析】全等三角形面积相等,周长相等;
6.【答案】40°;
【解析】见“比例”设,用三角形内角和为180°求解.
7.
【答案】70°;
【解析】∵∠B=24°,∠CAB=54°,∠DAC=16°,∴∠AFB=180°﹣(∠B+∠CAB+∠DAC)=86°,∴∠GFD=∠AFB=86°,∵△ABC≌△ADE,∠B=24°,∴∠D=∠B=24°,∴∠DGB=180°﹣∠D﹣∠DFG=70°.
8.
【答案】7;
【解析】BC与DE是对应边;
9.【答案】AD
C
80°;
【解析】∠BAC=∠DAE=120°-40°=80°;
10.【答案】30°;
【解析】解:∵△ACB≌△A′CB′,
∴∠ACB=∠A′CB′,
∵∠BCB′=∠A′CB′﹣∠A′CB,
∴∠ACA′=∠ACB﹣∠A′CB,
∴∠ACA′=∠BCB′=30°.
故答案为:30°.
11.【答案】40°;
【解析】∠DEF=∠ABC=×180°=40°;
12.【答案】平行;
【解析】由全等三角形性质可知∠B=∠D,所以AB∥CD.
三.解答题
1.【解析】
解:
在△ABC中,
∠ACB=180°-∠A-∠B,
又∠A=30°,∠B=50°,
所以∠ACB=100°.
又因为△ABC≌△DEF,
所以∠ACB=∠DFE,BC=EF(全等三角形对应角相等,对应边相等)
所以∠DFE=100°
EC=EF-FC=BC-FC=BF=2.
2.
【解析】
解:(1)△ABC≌△DEF;
(2)AB=DE,BC=EF,AC=DF;∠A=∠D,∠B=∠E,∠ACB=∠DFE;
(3)BC∥EF,AB∥DE,
理由是:
∵△ABC≌△DEF,
∴∠A=∠D,∠ACB=∠DFE,
∴AB∥DE,BC∥EF.
3.
【解析】
AE=DE
,且AE⊥DE
证明:
∵△ABE≌△ECD,
∴∠B=∠C,∠A=∠DEC,∠AEB=∠D,AE=DE
又∵AB⊥BC
∴∠A+∠AEB=90°,即∠DEC+∠AEB=90°
∴AE⊥DE
∴AE与DE垂直且相等.
4.【解析】DE与AB互相垂直.
∵△ABC≌△DFC
∴∠A=∠D,∠B=∠CFD,
又∵∠ACB=90°
∴∠B+∠A=90°,而∠AFE=∠CFD
∴∠AFE+∠A=90°,即DE⊥AB.
5.【解析】
解:∵∠A=30°,∠B=50°,
∴∠ACB=180°﹣∠A﹣∠B=180°﹣30°﹣50°=100°,
∵△ABC≌△DEF,
∴∠DFE=∠ACB=100°,EF=BC,
∴EF﹣CF=BC﹣CF,即EC=BF,
∵BF=2,
∴EC=2.
6.【解析】
(1)△EAD≌△,其中∠EAD=∠,;
(2)∠1=180°-2,∠2=180°-2;
(3)规律为:∠1+∠2=2∠A.
全等三角形巩固练习
【巩固练习】
一、选择题
1.
如图所示,△ABC≌△DEC,则不能得到的结论是(
)
A.
AB=DE
B.
∠A=∠D
C.
BC=CD
D.
∠ACD=∠BCE
2.
如图,△ABC≌△BAD,A和B,C和D分别是对应顶点,若AB=6,AC=4,BC=5,则AD的长为(
)
A.
4
B.
5
C.
6
D.
以上都不对
3.
下列说法中正确的有(
)
①形状相同的两个图形是全等图形
②对应角相等的两个三角形是全等三角形
③全等三角形的面积相等
④若△ABC≌△DEF,△DEF
≌△MNP,△ABC≌△MNP.
A.0个
B.1个
C.2个
D.3个
4.
如图,△ABC≌△A′B′C,∠ACB=90°,∠A′CB=20°,则∠BCB′的度数为( )
A.20°
B.40°
C.70°
D.90°
5.
已知△ABC≌△DEF,BC=EF=6cm,△ABC的面积为18平方厘米,则EF边上的高是(
)
A.6cm
B.7cm
C.8cm
D.9cm
6.
将一张长方形纸片按如图所示的方式折叠,BC、BD分别为折痕,则∠CBD的度数为( )
A.60°
B.75° C.90°
D.95°
7.下列命题中,真命题的个数是
(
)
①全等三角形的周长相等
②全等三角形的对应角相等
③全等三角形的面积相等
④面积相等的两个三角形全等
A.4个
B.3个
C.2个
D.1个
8.如图,△ABC≌△ADE,若∠B=80°,∠C=30°,∠DAB:∠DAC=4:3,则∠EFC的度数为( )
A.30°
B.40°
C.70°
D.80°
9.下列命题中:⑴形状相同的两个三角形是全等形;⑵在两个三角形中,相等的角是对应角,相等的边是对应边;⑶全等三角形对应边上的高、中线及对应角平分线分别相等,其中真命题的个数有(
)
A.3个
B.2个
C.1个
D.0个
10.△ABC≌△DEF,且△ABC的周长为100,A、B分别与D、E对应,且AB=35,DF=30,则EF的长为( )
A.35
B.30
C.45
D.55
11.如图,已知△ACE≌△DFB,下列结论中正确的个数是( )
①AC=DB;②AB=DC;③∠1=∠2;④AE∥DF;⑤S△ACE=S△DFB;⑥BC=AE;⑦BF∥EC.
12.如图,△ABE≌△ACD,AB=AC,
BE=CD,
∠B=50°,∠AEC=120°,则∠DAC的度数为
(
)
A.120°
B.70
°
C.60°
D.50°
二、填空题
1.如图所示,△AOB≌△COD,∠AOB=∠COD,∠A=∠C,则∠D的对应角是___________,图中相等的线段有____________________________.
2.如图,△ABC≌△A′B′C′,其中∠A=36°,∠C′=24°,则∠B=___________.
3.
已知△DEF≌△ABC,AB=AC,且△ABC的周长为23,BC=4,则△DEF的边中必有一条边等于______.
4.
如图,如果将△ABC向右平移CF的长度,则与△DEF重合,那么图中相等的线段有__________;若∠A=46°,则∠D=________.
5.已知△ABC≌△,若△ABC的面积为10
,则△的面积为________
,若△的周长为16,则△ABC的周长为________.
6.
△ABC中,∠A∶∠C∶∠B=4∶3∶2,且△ABC≌△DEF,则∠DEF=______
.
7.
如图,△ABC≌△ADE,BC的延长线交DE于点G,若∠B=24°,∠CAB=54°,∠DAC=16°,则∠DGB=
.
8.
如图,△ABC≌△ADE,如果AB=5,BC=7,AC=6,那么DE的长是________.
9.
如图,△ABC≌△ADE,则,AB=
,∠E
=∠
;若∠BAE=120°,∠BAD=40°,则∠BAC=___________.
10.如图,△ACB≌△A′CB′,∠BCB′=30°,则∠ACA′的度数为 __________.
11.
△ABC中,∠A∶∠C∶∠B=4∶3∶2,且△ABC≌△DEF,则∠DEF=______
12.
如图,AC、BD相交于点O,△AOB≌△COD,则AB与CD的位置关系是
.
三、解答题
1.如图,已知△ABC≌△DEF,∠A=30°,∠B=50°,BF=2,求∠DFE的度数与EC的长.
2.如图,在图中的两个三角形是全等三角形,其中A和D、B和E是对应点.
(1)用符号“≌“表示这两个三角形全等(要求对应顶点写在对应位置上);
(2)写出图中相等的线段和相等的角;
(3)写出图中互相平行的线段,并说明理由.
3.
如图,E为线段BC上一点,AB⊥BC,△ABE≌△ECD.判断AE与DE的关系,并证明你的结论.
4.
如图,△ABC中,∠ACB=90°,△ABC≌△DFC,你能判断DE与AB互相垂直吗?说出你的理由.
5.如图,已知△ABC≌△DEF,∠A=30°,∠B=50°,BF=2,求∠DFE的度数和EC的长.
6.如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,
(1)写出图中一对全等的三角形,并写出它们的所有对应角;
(2)设的度数为,∠的度数为,那么∠1,∠2的度数分别是多少?(用含有或的代数式表示)
(3)∠A与∠1+∠2之间有一种数量关系始终保持不变,请找出这个规律.
【答案与解析】
一.选择题
1.
【答案】C;
【解析】因为△ABC≌△DEC,可得:AB=DE,∠A=∠D,BC=EC,∠ACD=∠BCE,
故选C.
2.
【答案】B;
【解析】AD与BC是对应边,全等三角形对应边相等.
3.
【答案】C;
【解析】③和④是正确的;
4.
【答案】C;
【解析】解:∵△ACB≌△A′CB′,
∴∠ACB=∠A′CB′,
∴∠BCB′=∠A′CB′﹣∠A′CB=70°.
故选C.
5.
【答案】A;
【解析】EF边上的高=;
6.
【答案】C;
【解析】折叠所成的两个三角形全等,找到对应角可解.
7.
【答案】
B;
【解析】①②③是正确的;
8.
【答案】C;
【解析】∵∠B=80°,∠C=30°,∴∠BAC=180°﹣∠B﹣∠C=70°,∵△ABC≌△ADE,
∴∠DAE=∠BAC=70°,∠E=∠C=30°.∵∠DAB:∠DAC=4:3,∴∠DAB=40°,∠DAC=30°,
∴∠EAC=∠DAE﹣∠DAC=70°﹣30°=40°,∴∠EFC=∠E+∠EAC=30°+40°=70°.
9.
【答案】C;
【解析】只有(3)是正确的命题;
10.
【答案】A;
【解析】AC=DF=30,EF=BC=100-35-30=35;
11.
【答案】C;
【解析】解:∵△ACE≌△DFB,
∴AC=DB,①正确;
∠ECA=∠DBF,∠A=∠D,S△ACE=S△DFB,⑤正确;
∵AB+BC=CD+BC,
∴AB=CD
②正确;
∵∠ECA=∠DBF,
∴BF∥EC,⑦正确;
∠1=∠2,③正确;
∵∠A=∠D,
∴AE∥DF,④正确.
BC与AE,不是对应边,也没有办法证明二者相等,⑥不正确.
故选C.
12.
【答案】B;
【解析】由全等三角形的性质,易得∠BAD=∠CAE=10°,∠BAC=80°,所以∠DAC=70°.
二.填空题
1.
【答案】∠OBA,OA=OC、OB=OD、AB=CD;
【解析】解:∵△AOB≌△COD,∠AOB=∠COD,∠A=∠C,
∴∠D=∠OBA,OA=OC、OB=OD、AB=CD,
故答案为:∠OBA,OA=OC、OB=OD、AB=CD.
2.
【答案】120°;
【解析】∵△ABC≌△A′B′C′,∴∠C=∠C′=24°,∴∠B=180°﹣∠A﹣∠B=120°.
3.
【答案】4或9.5;
【解析】DE=DF=9.5,EF=4;
4.【答案】AB=DE、AC=DF、BC=EF、BE=CF,
46°;
5.【答案】10,16;
【解析】全等三角形面积相等,周长相等;
6.【答案】40°;
【解析】见“比例”设,用三角形内角和为180°求解.
7.
【答案】70°;
【解析】∵∠B=24°,∠CAB=54°,∠DAC=16°,∴∠AFB=180°﹣(∠B+∠CAB+∠DAC)=86°,∴∠GFD=∠AFB=86°,∵△ABC≌△ADE,∠B=24°,∴∠D=∠B=24°,∴∠DGB=180°﹣∠D﹣∠DFG=70°.
8.
【答案】7;
【解析】BC与DE是对应边;
9.【答案】AD
C
80°;
【解析】∠BAC=∠DAE=120°-40°=80°;
10.【答案】30°;
【解析】解:∵△ACB≌△A′CB′,
∴∠ACB=∠A′CB′,
∵∠BCB′=∠A′CB′﹣∠A′CB,
∴∠ACA′=∠ACB﹣∠A′CB,
∴∠ACA′=∠BCB′=30°.
故答案为:30°.
11.【答案】40°;
【解析】∠DEF=∠ABC=×180°=40°;
12.【答案】平行;
【解析】由全等三角形性质可知∠B=∠D,所以AB∥CD.
三.解答题
1.【解析】
解:
在△ABC中,
∠ACB=180°-∠A-∠B,
又∠A=30°,∠B=50°,
所以∠ACB=100°.
又因为△ABC≌△DEF,
所以∠ACB=∠DFE,BC=EF(全等三角形对应角相等,对应边相等)
所以∠DFE=100°
EC=EF-FC=BC-FC=BF=2.
2.
【解析】
解:(1)△ABC≌△DEF;
(2)AB=DE,BC=EF,AC=DF;∠A=∠D,∠B=∠E,∠ACB=∠DFE;
(3)BC∥EF,AB∥DE,
理由是:
∵△ABC≌△DEF,
∴∠A=∠D,∠ACB=∠DFE,
∴AB∥DE,BC∥EF.
3.
【解析】
AE=DE
,且AE⊥DE
证明:
∵△ABE≌△ECD,
∴∠B=∠C,∠A=∠DEC,∠AEB=∠D,AE=DE
又∵AB⊥BC
∴∠A+∠AEB=90°,即∠DEC+∠AEB=90°
∴AE⊥DE
∴AE与DE垂直且相等.
4.【解析】DE与AB互相垂直.
∵△ABC≌△DFC
∴∠A=∠D,∠B=∠CFD,
又∵∠ACB=90°
∴∠B+∠A=90°,而∠AFE=∠CFD
∴∠AFE+∠A=90°,即DE⊥AB.
5.【解析】
解:∵∠A=30°,∠B=50°,
∴∠ACB=180°﹣∠A﹣∠B=180°﹣30°﹣50°=100°,
∵△ABC≌△DEF,
∴∠DFE=∠ACB=100°,EF=BC,
∴EF﹣CF=BC﹣CF,即EC=BF,
∵BF=2,
∴EC=2.
6.【解析】
(1)△EAD≌△,其中∠EAD=∠,;
(2)∠1=180°-2,∠2=180°-2;
(3)规律为:∠1+∠2=2∠A.
