2021-2022学年九年级数学上册同步(人教版)22.3实际问题与二次函数-同步练习(word版含答案)
文档属性
| 名称 | 2021-2022学年九年级数学上册同步(人教版)22.3实际问题与二次函数-同步练习(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 576.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-30 14:12:44 | ||
图片预览



文档简介
22.3实际问题与二次函数(1)-同步练习-2021-2022学年九年级数学上册同步(人教版)
时间:60分钟
一、单选题
1.某童装专卖店销售一批某品牌童装,已知销售这种童装每天获得的利润y(元)与童装的销售价x(元/件)之间的函数解析式为y=﹣x2+160x﹣4800.若想每天获得的利润最大,则销售价应定为( )
A.110元/件
B.100元/件
C.90元/件
D.80元/件
2.某种正方形合金板材的成本y(元)与它的面积成正比,设边长为xcm.当x=3时,y=18,那么当成本为72元时,边长为(
)
A.6cm
B.12cm
C.24cm
D.36cm
3.下表所列为某商店薄利多销的情况,某商品原价为元,随着不同幅度的降价,日销量(单位为件)发生相应的变化.如果售价为元时,日销量为(
)件.
降价(元)
日销量(件)
A.1200
B.750
C.1110
D.1140
4.三孔桥横截面的三个孔都呈抛物线形,两小孔形状、大小完全相同.当水面刚好淹没小孔时,大孔水面宽度为10米,孔顶离水面1.5米;当水位下降,大孔水面宽度为14米时,单个小孔的水面宽度为4米,若大孔水面宽度为20米,则单个小孔的水面宽度为( )
A.4米
B.5米
C.2米
D.7米
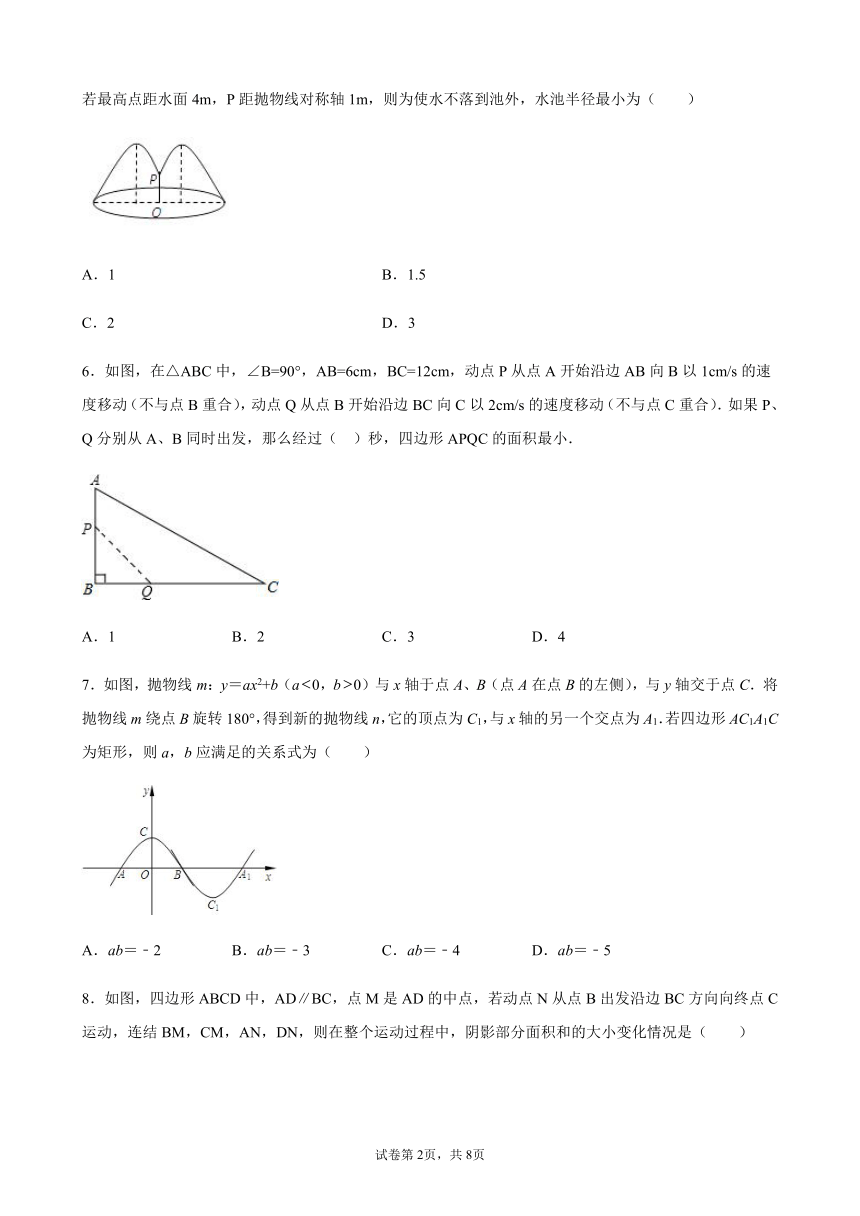
5.如图,花坛水池中央有一喷泉,水管OP=3m,水从喷头P喷出后呈抛物线状先向上至最高点后落下,若最高点距水面4m,P距抛物线对称轴1m,则为使水不落到池外,水池半径最小为( )
A.1
B.1.5
C.2
D.3
6.如图,在△ABC中,∠B=90°,AB=6cm,BC=12cm,动点P从点A开始沿边AB向B以1cm/s的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以2cm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,那么经过( )秒,四边形APQC的面积最小.
A.1
B.2
C.3
D.4
7.如图,抛物线m:y=ax2+b(a0,b0)与x轴于点A、B(点A在点B的左侧),与y轴交于点C.将抛物线m绕点B旋转180°,得到新的抛物线n,它的顶点为C1,与x轴的另一个交点为A1.若四边形AC1A1C为矩形,则a,b应满足的关系式为( )
A.ab=﹣2
B.ab=﹣3
C.ab=﹣4
D.ab=﹣5
8.如图,四边形ABCD中,AD∥BC,点M是AD的中点,若动点N从点B出发沿边BC方向向终点C运动,连结BM,CM,AN,DN,则在整个运动过程中,阴影部分面积和的大小变化情况是( )
A.不变
B.一直变大
C.先减小后增大
D.先增大后减小
二、填空题
9.一件工艺品进价为100元,标价135元售出,每天可售出100件.
根据销售统计,一件工艺品每降价1元出售,则每天可多售出4件,要使每天获得的利润最大,每件需降价的钱数为_______元.
10.某种商品每件进价为20元,调查表明:在某段时间内若以每件x元(,且x为整数)出售,可卖出件,若使利润最大,则每件商品的售价应为_______元.
11.如果周长为20的长方形一边为,那么它的面积关于的函数解析式是__________
12.如图,在平面直角坐标系中,抛物线经过平移得到抛物线,其对称轴与两段抛物线所围成的阴影部分的面积是_______
13.如图,在中,,,,动点从点开始沿边向以2的速度移动(不与点重合),动点从点开始沿边向以4的速度移动(不与点重合).如果、分别从、同时出发,那么经过______秒,四边形的面积最小.
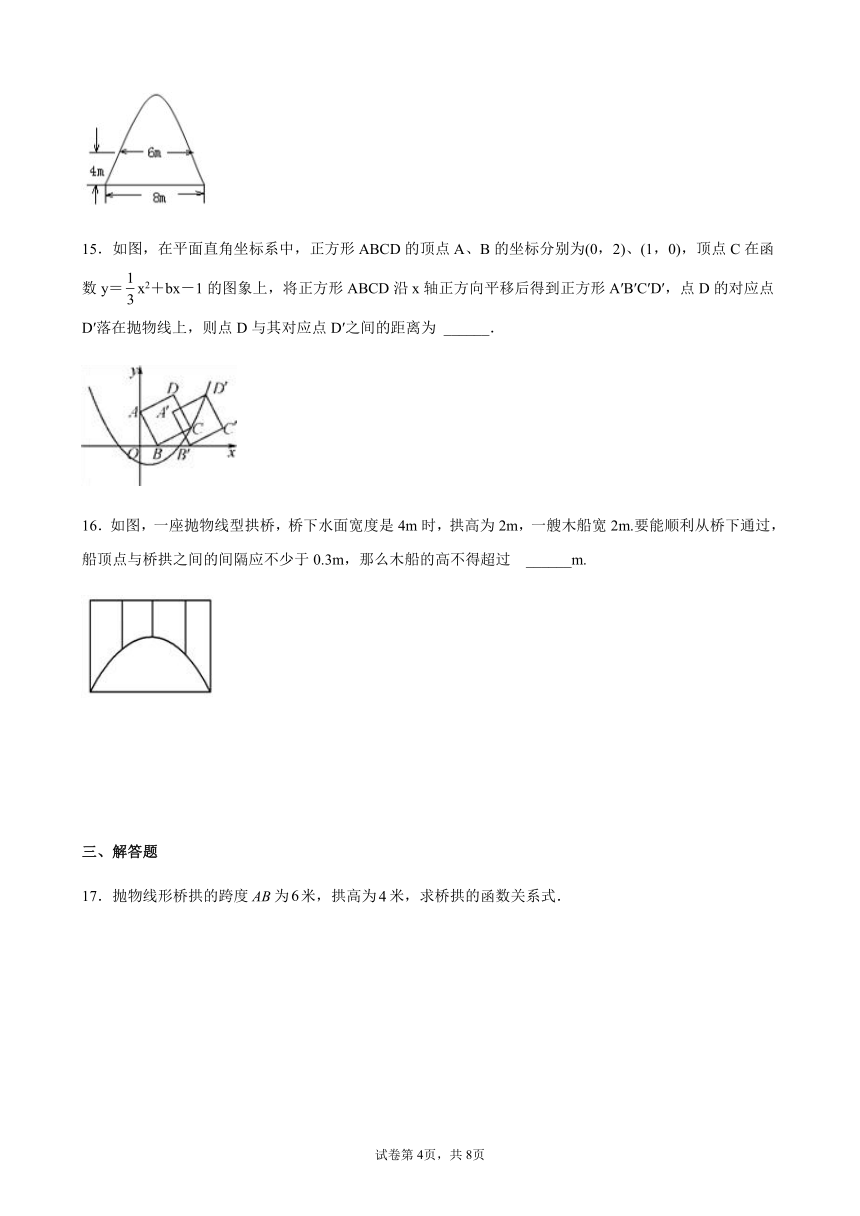
14.如图,有一个横截面边缘为抛物线的隧道入口,隧道入口处的底面宽度为,两侧距底面高处各有一盏灯,两灯间的水平距离为,则这个隧道入口的最大高度为_________.
15.如图,在平面直角坐标系中,正方形ABCD的顶点A、B的坐标分别为(0,2)、(1,0),顶点C在函数y=x2+bx-1的图象上,将正方形ABCD沿x轴正方向平移后得到正方形A′B′C′D′,点D的对应点D′落在抛物线上,则点D与其对应点D′之间的距离为
______.
16.如图,一座抛物线型拱桥,桥下水面宽度是4m时,拱高为2m,一艘木船宽2m.要能顺利从桥下通过,船顶点与桥拱之间的间隔应不少于0.3m,那么木船的高不得超过
______m.
三、解答题
17.抛物线形桥拱的跨度为米,拱高为米,求桥拱的函数关系式.
18.如图,在中,,,,动点从点开始沿边向点以2速度移动.动点从点开始沿边向点以4的速度移动,如果、分别从点、同时出发,那么的面积随出发时间如何变化?(写出函数解析式及的取值范围)
19.我国中东部地区雾霾天气趋于严重,环境治理已刻不容缓。某市某电器商场根据民众健康需要,代理销售某种空气净化器,其进价时元/台。经过市场销售后发现:在一个月内,当售价是元/台时,可售出台,且售价每降低元,就可多售出台。若供货商规定这种空气净化器售价不能低于元/台,代理销售商每月要完成不低于台的销售任务。
(1)求出月销售量(单位:台)与售价(单位:元/台)之间的函数关系式,并求出自变量的取值范围;
(2)当售价定为多少时,商场每月销售这种空气净化器所获得的利润(单位:元)最大?最大利润是多少?
20.如图,隧道的截面由抛物线和长方形构成.长方形的长为16m,宽为6m,抛物线的最高点C离路面AA1的距离为8m.
(1)建立适当的坐标系,求出表示抛物线的函数表达式;
(2)一大型货车装载设备后高为7m,宽为4m.如果隧道内设双向行驶车道,那么这辆货车能否安全通过?
21.某市场销售一批名牌衬衫,平均每天可销售20件,每件赢利40元.为了扩大销售,增加赢利,尽快减少库存,商场决定采取适当降价措施.经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件.求:
(1)若商场平均每天要赢利1200元,每件衬衫应降价多少元?
(2)要使商场平均每天赢利最多,请你帮助设计方案.
22.如图,在平面直角坐标系中,二次函数y=﹣x2+6x﹣5的图象与x轴交于A、B两点,与y轴交于点C,其顶点为P,连接PA、AC、CP,过点C作y轴的垂线l.
(1)P的坐标
,C的坐标
;
(2)直线1上是否存在点Q,使△PBQ的面积等于△PAC面积的2倍?若存在,求出点Q的坐标;若不存在,请说明理由.
23.用配方法可以解一元二次方程,还可以用它来解决很多问题.例如:因为,所以就有最小值,即,只有当时,才能得到这个式子的最小值.同样,因为,所以有最大值,即,只有在时,才能得到这个式子的最大值.
(1)当
时,代数式有最
(填写大或小)值为
.
(2)当
时,代数式有最
(填写大或小)值为
.
(3)矩形花园的一面靠墙,围成花园的栅栏总长度是,当花园与墙平行的边长为多少时,花园的面积最大?最大面积是多少?(提示:可设与墙垂直的边长为,用含的代数式表示花园的面积)
24.如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度a为10m),围成中间隔有一道篱笆的长方形花圃(由两个小矩形花圃组成).设花圃的一边AB为xm,面积为Sm2.
(1)求S与x之间的函数表达式(写出自变量的取值范围).
(2)如果要围成面积为45m2的花圃,那么AB的长是多少米?
(3)能围成面积比45m2更大的花圃吗?如果能,请求出最大面积,并说明围法;如果不能,请说明理由.
试卷第1页,共3页
参考答案
1.D
【解析】解:∵y=﹣x2+160x﹣4800,
∴抛物线的开口向下,
∴当x=﹣=80时,y==1600,
∴想每天获得的利润最大,则销售价应定为80元,
故选:D.
2.A
【解析】解:设y与x之间的函数关系式为y=kx2,由题意,得
18=9k,
解得:k=2,
∴y=2x2,
当y=72时,72=2x2,
∴x=6.
故选A.
3.C
【解析】解:由表中数据得,每降元,销售量增加件,
即每降元,销售量增加件,
降元时,销售量为(件).
故答案为:.
4.B
【解析】解:如图,建立如图所示的平面直角坐标系,由题意可得MN=4,EF=14,BC=10,DO=,
设大孔所在抛物线解析式为y=ax2+,
∵BC=10,
∴点B(﹣5,0),
∴0=a×(﹣5)2+,
∴a=-,
∴大孔所在抛物线解析式为y=-x2+,设点A(b,0),则设顶点为A的小孔所在抛物线的解析式为y=m(x﹣b)2,
∵EF=14,
∴点E的横坐标为-7,
∴点E坐标为(-7,-),
∴-=m(x﹣b)2,
∴x1=+b,x2=-+b,
∴MN=4,
∴|+b-(-+b)|=4
∴m=-,
∴顶点为A的小孔所在抛物线的解析式为y=-(x﹣b)2,
∵大孔水面宽度为20米,
∴当x=-10时,y=-,
∴-=-(x﹣b)2,
∴x1=+b,x2=-+b,
∴单个小孔的水面宽度=|(+b)-(-+b)|=5(米),
故选:B.
5.D
【解析】如图建立坐标系:
抛物线的顶点坐标是(1,4),
设抛物线的解析式是y=a(x-1)2+4,
把(0,3)代入解析式得:a+4=3,
解得:a=-1,
则抛物线的解析式是:y=-(x-1)2+4,
当y=0时,-(x-1)2+4=0,
解得:x1=3,x2=-1(舍去),
则水池的最小半径是3米.
故选:D.
6.C
【解析】解:设P、Q同时出发后经过的时间为ts,四边形APQC的面积为Scm2,则有:
S=S△ABC-S△PBQ
=
×12×6-
(6-t)×2t
=t2-6t+36
=(t-3)2+27.
∴当t=3s时,S取得最小值.
故选C.
7.B
【解析】解:令x=0,得:y=b.
∴C(0,b).
令y=0,得:ax2+b=0,
∵,
∴x=±,
∴A(﹣,0),B(,0),
∴AB=2,BC=,
要使平行四边形AC1A1C是矩形,必须满足AB=BC,
∴,
∴,
∴ab=﹣3,
∴a,b应满足关系式ab=﹣3,
故选:B.
8.C
【解析】解:连接MN,
∵AD∥BC
∴S△ABM=S△NMA,
∴△AEB与△NME的面积相等,同理△NMF与△CDF的面积相等,
∴S阴影=S四边形ABCD﹣2S四边形MENF,
设AM=MD=a,BC=b,BN=x,S△AMN=S△DMN=k,k为常数
∴
所以S△AEM:S△AMN=
∴S△AEM=
同理S△DFM=
令S=S△AEM+S△DFM=
=,其分子为常数
令y=(a+x)(a+b﹣x)=-x2+bx+a2+ab
它的对称轴为x=,开口向下
当0<x<时,y随x的增大而增大,此时S随着x的增大而减小
所以S四边形MENF=随x的增大而增大
所以S空白=2S四边形MENF随x的增大而增大
所以S阴影随x的增大而减小
当<x<b时,y随x的增大而减小,此时S随着x的增大而增大
所以S阴影随x的增大而增大
综上所述:S阴影先减小后增大
故选:C.
9.5
【解析】设每件需降价的钱数为x元,每天获利y元,
则y=(135﹣x﹣100)(100+4x),
即y=﹣4(x﹣5)2+3600,
∵﹣4<0,
∴当x=5时,每天获利的y值最大.
故答案为5.
10.25
【解析】解:设利润为w元,
则w=(x-20)(30-x)=-(x-25)2+25,
∵20≤x≤30,
∴当x=25时,二次函数有最大值25,
故答案是:25.
11.y=x(10-x)
【解析】解:由周长为20的长方形一边为,
可知长方形另一边为10-x,
∴它的面积是x(10-x)
∴y=x(10-x);
故答案为:y=x(10x)
.
12.4
【解析】∵,
∴平移后抛物线的顶点坐标为(2, 2),对称轴为直线x=2,
当x=2时,,
∴平移后阴影部分的面积等于如图三角形的面积,
×(2+2)×2=4,
故填:4.
13.3
【解析】解:设P、Q同时出发后经过的时间为ts,四边形APQC的面积为Scm2,则有:
S=S△ABC-S△PBQ=×12×6-(6-t)×2t
=t2-6t+36
=(t-3)2+27.
∴当t=3s时,S取得最小值.
故填:3.
14.
【解析】解:如图,建立平面直角坐标系,
设抛物线解析式为:,
设,,
将点A和点B代入解析式,得,解得,
∴,,
则最大高度是.
故答案是:.
15.2
【解析】如图,过C作GH⊥x轴,交x轴于G,过D作DH⊥GH于H,由正方形的性质和A、B点的坐标证得△AOB≌△BGC,然后根据全等三角形的性质求得C点(3,1),利用点C的坐标代入函数的解析式y=x2+bx-1,求得b=-,同理得到△AOB≌△BGC,得出D的坐标(2,3),根据平移的性质:D、D′纵坐标相同,则y=3,代入函数的解析式x2-x-1=3,解得x=4或x=-3(舍去),求出D′点的坐标为(4,3),即可得D与D′的距离为2.
故答案为2.
16.1.2
【解析】以水面所在水平线为x轴,过拱桥顶点作水平线的垂线,作为y轴,建立坐标系,
设水平面与拱桥的交点为A(-2,0),B(2,0),C(0,2),
利用待定系数法设函数的解析式为y=a(x+2)(x-2)代入点C坐标,
求得a=-,
即抛物线的解析式为y=-(x+2)(x-2),
令x=1,解得y=1.5,
船顶与桥拱之间的间隔应不少于0.3,则木船的最高高度为1.5-0.3=1.2米.
故答案为:1.2.
17.(答案不唯一).
【解析】解:以所在直线为轴,中点为原点建立直角坐标系,
∵AB=6
∴AO=3
∴点A的坐标为(-3,0)
可设所求解析式为,
由抛物线过和得:
解得:
∴抛物线解析式为(答案不唯一).
18..
【解析】
当P运动到点C或Q运动到点C停止,此时
所以t的取值范围为
19.(1)y=-10x+4200,;(2)310,121000
【解析】解:(1)根据题中条件销售价每降低5元,月销售量就可多售出50台,
当售价为x时,降了(400-x),所以月销售多了10(400-x)台,
则月销售量y(台)与售价x(元/台)之间的函数关系式;y=10(400-x)+200=-10x+4200
∵空气净化器售价不能低于元/台,代理销售商每月要完成不低于台
∴解得
(2)由题意有:w=
=
=
=
∴当售价定为310元时,w有最大值,为121000
20.(1)以AA1所在直线为x轴,以线段AA1的中点为坐标原点建立平面直角坐标系,
;(2)货运卡车能通过.
【解析】解:(1)如图,以AA1所在直线为x轴,以线段AA1的中点为坐标原点建立平面直角坐标系,
根据题意得A(﹣8,0),B(﹣8,6),C(0,8),
设抛物线的解析式为y=ax2+8,把B(﹣8,6)代入,得:
64a+8=6,
解得:a=﹣.
∴抛物线的解析式为y=﹣x2+8.
(2)根据题意,把x=±4代入解析式y=﹣x2+8,
得y=7.5m.
∵7.5m>7m,
∴货运卡车能通过.
21.(1)20元;(2)每件衬衫应降价15元,商场盈利最多,共1250元.
【解析】解:设每天利润为w元,每件衬衫降价x元,
根据题意得
(1)当时,,
解之得.
根据题意要尽快减少库存,所以应降价20元.
答:每件衬衫应降价20元.
(2)解:商场每天盈利w=.
∵-2<0
∴抛物线开口向下
∴当x=15时,w有最大值,w的最大值为1250,
所以当每件衬衫应降价15元时,商场盈利最多,共1250元.
答:每件衬衫降价15元时,商场平均每天盈利最多.
22.(1)(3,4),(0,﹣5);(2)存在,点Q的坐标为:(,﹣5)或(,﹣5)
【解析】解:(1)∵y=﹣x2+6x﹣5=﹣(x﹣3)2+4,
∴顶点P(3,4),
令x=0得到y=﹣5,
∴C(0,﹣5).
故答案为:(3,4),(0,﹣5);
(2)令y=0,x2﹣6x+5=0,
解得:x=1或x=5,
∴A(1,0),B(5,0),
设直线PC的解析式为y=kx+b,则有,
解得:,
∴直线PC的解析式为:y=3x﹣5,
设直线交x轴于D,则D(,0),
设直线PQ交x轴于E,当BE=2AD时,△PBQ的面积等于△PAC的面积的2倍,
∵AD=,
∴BE=,
∴E(,0)或E′(,0),
则直线PE的解析式为:y=﹣6x+22,
∴Q(,﹣5),
直线PE′的解析式为y=﹣x+,
∴Q′(,﹣5),
综上所述,满足条件的点Q的坐标为:(,﹣5)或(,﹣5);
23.(1);小;;(2);大;;(3)长为时,面积最大是.
【解析】解:(1)由代数式知:当-2时,代数式有最小值-3,
故填:,小,;
(2),
当时,代数式有最大值为,
故答案为:,大,;
(3)根据题意可得:当花园与墙相邻的宽为时,
,
当时,
S最大=,
长为时,面积最大是.
24.(1)S=-3x2+24x(≤x<8);(2)AB的长为5m;(3)能围成面积比45m2更大的花圃,最大面积为m2,,此时AB=m,BC=10m.
【解析】解:(1)
∵0<24 3x≤10,
∴≤x<8
∴S=x(24-3x)=-3x2+24x(≤x<8).
(2)当S=45时,有-3x2+24x=45.
解得x1=3,x2=5.
∵≤x<8,
∴x=5,
即AB的长为5m.
(3)能围成面积比45m2更大的花圃.
∵S=-3x2+24x=-3(x-4)2+48,其函数图象开口向下,对称轴为直线x=4,当x>4时,y随x的增大而减小,
∴在≤x<8的范围内,当x=时,S取得最大值,S最大值=.
即最大面积为m2,
此时AB=m,BC=10m.
答案第1页,共2页
答案第1页,共2页
时间:60分钟
一、单选题
1.某童装专卖店销售一批某品牌童装,已知销售这种童装每天获得的利润y(元)与童装的销售价x(元/件)之间的函数解析式为y=﹣x2+160x﹣4800.若想每天获得的利润最大,则销售价应定为( )
A.110元/件
B.100元/件
C.90元/件
D.80元/件
2.某种正方形合金板材的成本y(元)与它的面积成正比,设边长为xcm.当x=3时,y=18,那么当成本为72元时,边长为(
)
A.6cm
B.12cm
C.24cm
D.36cm
3.下表所列为某商店薄利多销的情况,某商品原价为元,随着不同幅度的降价,日销量(单位为件)发生相应的变化.如果售价为元时,日销量为(
)件.
降价(元)
日销量(件)
A.1200
B.750
C.1110
D.1140
4.三孔桥横截面的三个孔都呈抛物线形,两小孔形状、大小完全相同.当水面刚好淹没小孔时,大孔水面宽度为10米,孔顶离水面1.5米;当水位下降,大孔水面宽度为14米时,单个小孔的水面宽度为4米,若大孔水面宽度为20米,则单个小孔的水面宽度为( )
A.4米
B.5米
C.2米
D.7米
5.如图,花坛水池中央有一喷泉,水管OP=3m,水从喷头P喷出后呈抛物线状先向上至最高点后落下,若最高点距水面4m,P距抛物线对称轴1m,则为使水不落到池外,水池半径最小为( )
A.1
B.1.5
C.2
D.3
6.如图,在△ABC中,∠B=90°,AB=6cm,BC=12cm,动点P从点A开始沿边AB向B以1cm/s的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以2cm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,那么经过( )秒,四边形APQC的面积最小.
A.1
B.2
C.3
D.4
7.如图,抛物线m:y=ax2+b(a0,b0)与x轴于点A、B(点A在点B的左侧),与y轴交于点C.将抛物线m绕点B旋转180°,得到新的抛物线n,它的顶点为C1,与x轴的另一个交点为A1.若四边形AC1A1C为矩形,则a,b应满足的关系式为( )
A.ab=﹣2
B.ab=﹣3
C.ab=﹣4
D.ab=﹣5
8.如图,四边形ABCD中,AD∥BC,点M是AD的中点,若动点N从点B出发沿边BC方向向终点C运动,连结BM,CM,AN,DN,则在整个运动过程中,阴影部分面积和的大小变化情况是( )
A.不变
B.一直变大
C.先减小后增大
D.先增大后减小
二、填空题
9.一件工艺品进价为100元,标价135元售出,每天可售出100件.
根据销售统计,一件工艺品每降价1元出售,则每天可多售出4件,要使每天获得的利润最大,每件需降价的钱数为_______元.
10.某种商品每件进价为20元,调查表明:在某段时间内若以每件x元(,且x为整数)出售,可卖出件,若使利润最大,则每件商品的售价应为_______元.
11.如果周长为20的长方形一边为,那么它的面积关于的函数解析式是__________
12.如图,在平面直角坐标系中,抛物线经过平移得到抛物线,其对称轴与两段抛物线所围成的阴影部分的面积是_______
13.如图,在中,,,,动点从点开始沿边向以2的速度移动(不与点重合),动点从点开始沿边向以4的速度移动(不与点重合).如果、分别从、同时出发,那么经过______秒,四边形的面积最小.
14.如图,有一个横截面边缘为抛物线的隧道入口,隧道入口处的底面宽度为,两侧距底面高处各有一盏灯,两灯间的水平距离为,则这个隧道入口的最大高度为_________.
15.如图,在平面直角坐标系中,正方形ABCD的顶点A、B的坐标分别为(0,2)、(1,0),顶点C在函数y=x2+bx-1的图象上,将正方形ABCD沿x轴正方向平移后得到正方形A′B′C′D′,点D的对应点D′落在抛物线上,则点D与其对应点D′之间的距离为
______.
16.如图,一座抛物线型拱桥,桥下水面宽度是4m时,拱高为2m,一艘木船宽2m.要能顺利从桥下通过,船顶点与桥拱之间的间隔应不少于0.3m,那么木船的高不得超过
______m.
三、解答题
17.抛物线形桥拱的跨度为米,拱高为米,求桥拱的函数关系式.
18.如图,在中,,,,动点从点开始沿边向点以2速度移动.动点从点开始沿边向点以4的速度移动,如果、分别从点、同时出发,那么的面积随出发时间如何变化?(写出函数解析式及的取值范围)
19.我国中东部地区雾霾天气趋于严重,环境治理已刻不容缓。某市某电器商场根据民众健康需要,代理销售某种空气净化器,其进价时元/台。经过市场销售后发现:在一个月内,当售价是元/台时,可售出台,且售价每降低元,就可多售出台。若供货商规定这种空气净化器售价不能低于元/台,代理销售商每月要完成不低于台的销售任务。
(1)求出月销售量(单位:台)与售价(单位:元/台)之间的函数关系式,并求出自变量的取值范围;
(2)当售价定为多少时,商场每月销售这种空气净化器所获得的利润(单位:元)最大?最大利润是多少?
20.如图,隧道的截面由抛物线和长方形构成.长方形的长为16m,宽为6m,抛物线的最高点C离路面AA1的距离为8m.
(1)建立适当的坐标系,求出表示抛物线的函数表达式;
(2)一大型货车装载设备后高为7m,宽为4m.如果隧道内设双向行驶车道,那么这辆货车能否安全通过?
21.某市场销售一批名牌衬衫,平均每天可销售20件,每件赢利40元.为了扩大销售,增加赢利,尽快减少库存,商场决定采取适当降价措施.经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件.求:
(1)若商场平均每天要赢利1200元,每件衬衫应降价多少元?
(2)要使商场平均每天赢利最多,请你帮助设计方案.
22.如图,在平面直角坐标系中,二次函数y=﹣x2+6x﹣5的图象与x轴交于A、B两点,与y轴交于点C,其顶点为P,连接PA、AC、CP,过点C作y轴的垂线l.
(1)P的坐标
,C的坐标
;
(2)直线1上是否存在点Q,使△PBQ的面积等于△PAC面积的2倍?若存在,求出点Q的坐标;若不存在,请说明理由.
23.用配方法可以解一元二次方程,还可以用它来解决很多问题.例如:因为,所以就有最小值,即,只有当时,才能得到这个式子的最小值.同样,因为,所以有最大值,即,只有在时,才能得到这个式子的最大值.
(1)当
时,代数式有最
(填写大或小)值为
.
(2)当
时,代数式有最
(填写大或小)值为
.
(3)矩形花园的一面靠墙,围成花园的栅栏总长度是,当花园与墙平行的边长为多少时,花园的面积最大?最大面积是多少?(提示:可设与墙垂直的边长为,用含的代数式表示花园的面积)
24.如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度a为10m),围成中间隔有一道篱笆的长方形花圃(由两个小矩形花圃组成).设花圃的一边AB为xm,面积为Sm2.
(1)求S与x之间的函数表达式(写出自变量的取值范围).
(2)如果要围成面积为45m2的花圃,那么AB的长是多少米?
(3)能围成面积比45m2更大的花圃吗?如果能,请求出最大面积,并说明围法;如果不能,请说明理由.
试卷第1页,共3页
参考答案
1.D
【解析】解:∵y=﹣x2+160x﹣4800,
∴抛物线的开口向下,
∴当x=﹣=80时,y==1600,
∴想每天获得的利润最大,则销售价应定为80元,
故选:D.
2.A
【解析】解:设y与x之间的函数关系式为y=kx2,由题意,得
18=9k,
解得:k=2,
∴y=2x2,
当y=72时,72=2x2,
∴x=6.
故选A.
3.C
【解析】解:由表中数据得,每降元,销售量增加件,
即每降元,销售量增加件,
降元时,销售量为(件).
故答案为:.
4.B
【解析】解:如图,建立如图所示的平面直角坐标系,由题意可得MN=4,EF=14,BC=10,DO=,
设大孔所在抛物线解析式为y=ax2+,
∵BC=10,
∴点B(﹣5,0),
∴0=a×(﹣5)2+,
∴a=-,
∴大孔所在抛物线解析式为y=-x2+,设点A(b,0),则设顶点为A的小孔所在抛物线的解析式为y=m(x﹣b)2,
∵EF=14,
∴点E的横坐标为-7,
∴点E坐标为(-7,-),
∴-=m(x﹣b)2,
∴x1=+b,x2=-+b,
∴MN=4,
∴|+b-(-+b)|=4
∴m=-,
∴顶点为A的小孔所在抛物线的解析式为y=-(x﹣b)2,
∵大孔水面宽度为20米,
∴当x=-10时,y=-,
∴-=-(x﹣b)2,
∴x1=+b,x2=-+b,
∴单个小孔的水面宽度=|(+b)-(-+b)|=5(米),
故选:B.
5.D
【解析】如图建立坐标系:
抛物线的顶点坐标是(1,4),
设抛物线的解析式是y=a(x-1)2+4,
把(0,3)代入解析式得:a+4=3,
解得:a=-1,
则抛物线的解析式是:y=-(x-1)2+4,
当y=0时,-(x-1)2+4=0,
解得:x1=3,x2=-1(舍去),
则水池的最小半径是3米.
故选:D.
6.C
【解析】解:设P、Q同时出发后经过的时间为ts,四边形APQC的面积为Scm2,则有:
S=S△ABC-S△PBQ
=
×12×6-
(6-t)×2t
=t2-6t+36
=(t-3)2+27.
∴当t=3s时,S取得最小值.
故选C.
7.B
【解析】解:令x=0,得:y=b.
∴C(0,b).
令y=0,得:ax2+b=0,
∵,
∴x=±,
∴A(﹣,0),B(,0),
∴AB=2,BC=,
要使平行四边形AC1A1C是矩形,必须满足AB=BC,
∴,
∴,
∴ab=﹣3,
∴a,b应满足关系式ab=﹣3,
故选:B.
8.C
【解析】解:连接MN,
∵AD∥BC
∴S△ABM=S△NMA,
∴△AEB与△NME的面积相等,同理△NMF与△CDF的面积相等,
∴S阴影=S四边形ABCD﹣2S四边形MENF,
设AM=MD=a,BC=b,BN=x,S△AMN=S△DMN=k,k为常数
∴
所以S△AEM:S△AMN=
∴S△AEM=
同理S△DFM=
令S=S△AEM+S△DFM=
=,其分子为常数
令y=(a+x)(a+b﹣x)=-x2+bx+a2+ab
它的对称轴为x=,开口向下
当0<x<时,y随x的增大而增大,此时S随着x的增大而减小
所以S四边形MENF=随x的增大而增大
所以S空白=2S四边形MENF随x的增大而增大
所以S阴影随x的增大而减小
当<x<b时,y随x的增大而减小,此时S随着x的增大而增大
所以S阴影随x的增大而增大
综上所述:S阴影先减小后增大
故选:C.
9.5
【解析】设每件需降价的钱数为x元,每天获利y元,
则y=(135﹣x﹣100)(100+4x),
即y=﹣4(x﹣5)2+3600,
∵﹣4<0,
∴当x=5时,每天获利的y值最大.
故答案为5.
10.25
【解析】解:设利润为w元,
则w=(x-20)(30-x)=-(x-25)2+25,
∵20≤x≤30,
∴当x=25时,二次函数有最大值25,
故答案是:25.
11.y=x(10-x)
【解析】解:由周长为20的长方形一边为,
可知长方形另一边为10-x,
∴它的面积是x(10-x)
∴y=x(10-x);
故答案为:y=x(10x)
.
12.4
【解析】∵,
∴平移后抛物线的顶点坐标为(2, 2),对称轴为直线x=2,
当x=2时,,
∴平移后阴影部分的面积等于如图三角形的面积,
×(2+2)×2=4,
故填:4.
13.3
【解析】解:设P、Q同时出发后经过的时间为ts,四边形APQC的面积为Scm2,则有:
S=S△ABC-S△PBQ=×12×6-(6-t)×2t
=t2-6t+36
=(t-3)2+27.
∴当t=3s时,S取得最小值.
故填:3.
14.
【解析】解:如图,建立平面直角坐标系,
设抛物线解析式为:,
设,,
将点A和点B代入解析式,得,解得,
∴,,
则最大高度是.
故答案是:.
15.2
【解析】如图,过C作GH⊥x轴,交x轴于G,过D作DH⊥GH于H,由正方形的性质和A、B点的坐标证得△AOB≌△BGC,然后根据全等三角形的性质求得C点(3,1),利用点C的坐标代入函数的解析式y=x2+bx-1,求得b=-,同理得到△AOB≌△BGC,得出D的坐标(2,3),根据平移的性质:D、D′纵坐标相同,则y=3,代入函数的解析式x2-x-1=3,解得x=4或x=-3(舍去),求出D′点的坐标为(4,3),即可得D与D′的距离为2.
故答案为2.
16.1.2
【解析】以水面所在水平线为x轴,过拱桥顶点作水平线的垂线,作为y轴,建立坐标系,
设水平面与拱桥的交点为A(-2,0),B(2,0),C(0,2),
利用待定系数法设函数的解析式为y=a(x+2)(x-2)代入点C坐标,
求得a=-,
即抛物线的解析式为y=-(x+2)(x-2),
令x=1,解得y=1.5,
船顶与桥拱之间的间隔应不少于0.3,则木船的最高高度为1.5-0.3=1.2米.
故答案为:1.2.
17.(答案不唯一).
【解析】解:以所在直线为轴,中点为原点建立直角坐标系,
∵AB=6
∴AO=3
∴点A的坐标为(-3,0)
可设所求解析式为,
由抛物线过和得:
解得:
∴抛物线解析式为(答案不唯一).
18..
【解析】
当P运动到点C或Q运动到点C停止,此时
所以t的取值范围为
19.(1)y=-10x+4200,;(2)310,121000
【解析】解:(1)根据题中条件销售价每降低5元,月销售量就可多售出50台,
当售价为x时,降了(400-x),所以月销售多了10(400-x)台,
则月销售量y(台)与售价x(元/台)之间的函数关系式;y=10(400-x)+200=-10x+4200
∵空气净化器售价不能低于元/台,代理销售商每月要完成不低于台
∴解得
(2)由题意有:w=
=
=
=
∴当售价定为310元时,w有最大值,为121000
20.(1)以AA1所在直线为x轴,以线段AA1的中点为坐标原点建立平面直角坐标系,
;(2)货运卡车能通过.
【解析】解:(1)如图,以AA1所在直线为x轴,以线段AA1的中点为坐标原点建立平面直角坐标系,
根据题意得A(﹣8,0),B(﹣8,6),C(0,8),
设抛物线的解析式为y=ax2+8,把B(﹣8,6)代入,得:
64a+8=6,
解得:a=﹣.
∴抛物线的解析式为y=﹣x2+8.
(2)根据题意,把x=±4代入解析式y=﹣x2+8,
得y=7.5m.
∵7.5m>7m,
∴货运卡车能通过.
21.(1)20元;(2)每件衬衫应降价15元,商场盈利最多,共1250元.
【解析】解:设每天利润为w元,每件衬衫降价x元,
根据题意得
(1)当时,,
解之得.
根据题意要尽快减少库存,所以应降价20元.
答:每件衬衫应降价20元.
(2)解:商场每天盈利w=.
∵-2<0
∴抛物线开口向下
∴当x=15时,w有最大值,w的最大值为1250,
所以当每件衬衫应降价15元时,商场盈利最多,共1250元.
答:每件衬衫降价15元时,商场平均每天盈利最多.
22.(1)(3,4),(0,﹣5);(2)存在,点Q的坐标为:(,﹣5)或(,﹣5)
【解析】解:(1)∵y=﹣x2+6x﹣5=﹣(x﹣3)2+4,
∴顶点P(3,4),
令x=0得到y=﹣5,
∴C(0,﹣5).
故答案为:(3,4),(0,﹣5);
(2)令y=0,x2﹣6x+5=0,
解得:x=1或x=5,
∴A(1,0),B(5,0),
设直线PC的解析式为y=kx+b,则有,
解得:,
∴直线PC的解析式为:y=3x﹣5,
设直线交x轴于D,则D(,0),
设直线PQ交x轴于E,当BE=2AD时,△PBQ的面积等于△PAC的面积的2倍,
∵AD=,
∴BE=,
∴E(,0)或E′(,0),
则直线PE的解析式为:y=﹣6x+22,
∴Q(,﹣5),
直线PE′的解析式为y=﹣x+,
∴Q′(,﹣5),
综上所述,满足条件的点Q的坐标为:(,﹣5)或(,﹣5);
23.(1);小;;(2);大;;(3)长为时,面积最大是.
【解析】解:(1)由代数式知:当-2时,代数式有最小值-3,
故填:,小,;
(2),
当时,代数式有最大值为,
故答案为:,大,;
(3)根据题意可得:当花园与墙相邻的宽为时,
,
当时,
S最大=,
长为时,面积最大是.
24.(1)S=-3x2+24x(≤x<8);(2)AB的长为5m;(3)能围成面积比45m2更大的花圃,最大面积为m2,,此时AB=m,BC=10m.
【解析】解:(1)
∵0<24 3x≤10,
∴≤x<8
∴S=x(24-3x)=-3x2+24x(≤x<8).
(2)当S=45时,有-3x2+24x=45.
解得x1=3,x2=5.
∵≤x<8,
∴x=5,
即AB的长为5m.
(3)能围成面积比45m2更大的花圃.
∵S=-3x2+24x=-3(x-4)2+48,其函数图象开口向下,对称轴为直线x=4,当x>4时,y随x的增大而减小,
∴在≤x<8的范围内,当x=时,S取得最大值,S最大值=.
即最大面积为m2,
此时AB=m,BC=10m.
答案第1页,共2页
答案第1页,共2页
同课章节目录
