3.4 周长是多少 课件(共26张PPT)
文档属性
| 名称 | 3.4 周长是多少 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-29 20:20:56 | ||
图片预览






文档简介
(共26张PPT)
周长是多少(教材P46~47)
三年级数学·上
新课标[江苏]
第3单元
你们知道“凸”形图形的周长简便算法吗?
把每条边加起来就可以了呀!还有简便算法?
算一个长方形或正方形的面积也可以。
为什么可以这样算?
可以通过移边的方法使它变成规则图形!
知识点1
由几个相同正方形拼成的
图形,周长可能不相等
用6个边长1厘米的正方形可以拼成哪些不同的图形 拼成的图形周长各是多少厘米 它们的周长相等吗
探究方法
(1)用6个边长1厘米的正方形拼出你喜欢的图形。
(2)用算或数的方法,求出所拼图形的周长。
规范解答
(1)摆法一:
周长:1+6=7(厘米)
7×2=14(厘米)
规范解答
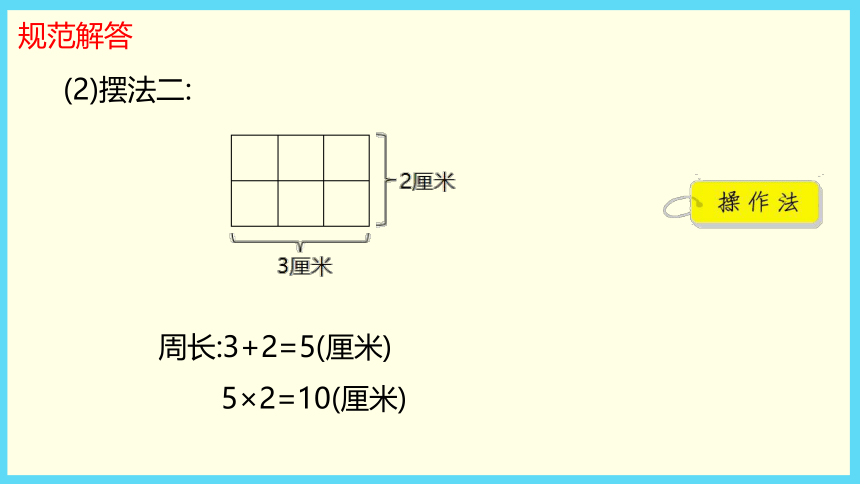
周长:3+2=5(厘米)
5×2=10(厘米)
(2)摆法二:
规范解答
周长:2+2+1+2+1+4=12(厘米)
(3)摆法三:
规范解答
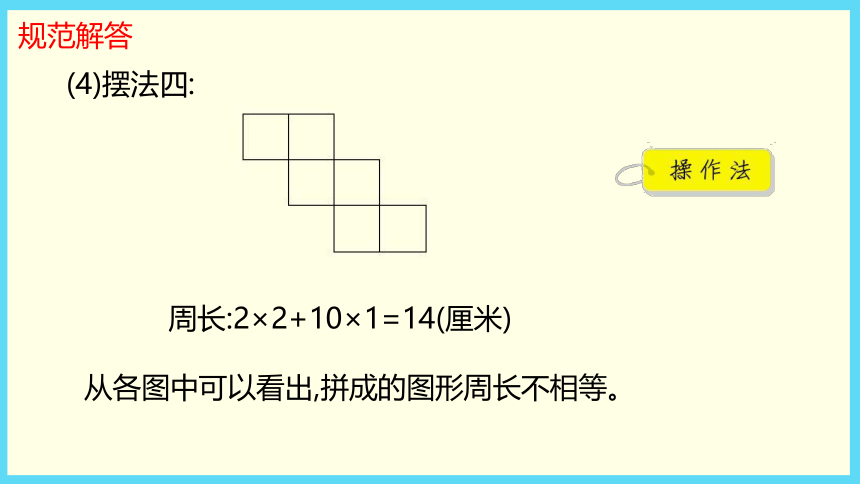
(4)摆法四:
周长:2×2+10×1=14(厘米)
从各图中可以看出,拼成的图形周长不相等。
规范解答
周长14厘米
周长10厘米
周长12厘米
周长14厘米
规范解答
周长14厘米
用6个边长1厘米的正方形可以拼成多种不同形状的图形,如上述4种图形,虽然都用了6个相同的小正方形,但是它们的周长可能会不相等。
周长10厘米
周长12厘米
周长14厘米
总结
计算一个图形周长的方法有很多,无论用什么方法算周长,一定要注意周长指的是一个图形外边一周的长度。用同样的正方形拼成不同形状的图形,它们的周长可能相等,也可能不相等。
知识点2
巧求周长
左边两个图形的周长各是多少厘米 它们的周长相等吗 (每个小方格的边长表示1厘米)
猜猜下面图形的周长是多少厘米,
和同学说说你的想法,再计算。
1
2
3
探究方法
方法一 数一数。
数出每个图形的周长是由几个小方格的边长组成的,再计算它们的周长。
图①:1×22=22(厘米)
图②:1×22=22(厘米)
图③:1×22=22(厘米)
三幅图的周长都相等。
探究方法
方法二 通过平移,图②和图③都转化成长6厘米、宽5厘米的长方形,与图①的长和宽相等。它们的周长都等于:(6+5)×2=22(厘米)(如图)。
图②
图③
规范解答
6+5=11(厘米)
11×2=22(厘米)
答:左边两个图形的周长相等,都是22厘米,右边图形的周长也是22厘米。
通过移一移、拼一拼的方法,把不规则图形转化成规则图形后,再按照周长的计算方法来计算就容易多了。
知识点3
画一画
你能在方格纸上画出周长是20厘米的长方形或正方形吗 能画出不同的长方形吗 (每个小方格的边长表示1厘米)
画出的长方形的长、宽各是
多少?正方形的边长呢?
理解题意
因为周长是20厘米,所以长方形的长、宽的和应等于10厘米,我们可以列出下表:
长
9厘米
8厘米
7厘米
6厘米
5厘米
宽
1厘米
2厘米
3厘米
4厘米
5厘米
周长
20厘米
20厘米
20厘米
20厘米
20厘米
正方形周长是20厘米
正方形边长=周长÷4
20÷4=5(厘米)
规范解答
如下图所示。
5厘米
5厘米
9厘米
1厘米
8厘米
2厘米
7厘米
3厘米
6厘米
4厘米
要画出给定周长的长方形,需要先计算出长方形的长与宽之和,才好画出图形;如果是画出正方形,那么需要先用“周长÷4”求出正方形的边长,再画图。
知识点4
估一估,量一量
下面两个图案的周长大约各是多少厘米 先估一估,再量一量。
你是怎样测量的?
你估计的怎么样?
估计 厘米
实际 厘米
估计 厘米
实际 厘米
五角星每边长约1厘米,共有10条边,笑脸的周长约有10厘米。
估算
量一量
用直尺测量出五角星一条边的长是1厘米,它的周长是1×10=10(厘米);用绳子绕笑脸一周,去掉多余的部分,伸直绳子,用直尺测量绳子的长是10厘米,即周长是10厘米。
比较估计与实际测量的结果,看估计是否准确
与同学交流估计方法
1.计算下面图形的周长。(单位:厘米)
同步练习
3+2=5(厘米)
3+5=8(厘米)
8+5=13(厘米)
13×2=26(厘米)
2
5
3
3
2
1
2
3
4
3+1+2=6(厘米)
6+4=10(厘米)
10×2=20(厘米)
20+2+2=24(厘米)
同步练习
2.请你在方格纸上画出周长是12厘米的长方形或正方形。能画出不同的长方形吗 (每个小方格的边长表示1厘米)
5厘米
1厘米
4厘米
2厘米
3厘米
第一个算出地球周长的人
2000多年前,有人用简单的测量工具计算出地球的周长,这个人就是古希腊的埃拉托色尼(约公元前275~前1940)。
埃拉托色尼博学多才,他不仅通晓天文,而且熟知地理;又是诗人、历史学家、语言学家、哲学家,曾担任过亚历山大博物馆的馆长。
细心的埃拉托色尼发现:离亚历山大城约800千米的塞恩城,夏日正午的阳光可以一直照到井底,因而这时候所有地面上的直立物都应该没有影子。但是,亚历山大城地面上的直立物却有一段很短的影子。他认为:直立物的影子是由亚历山大城的阳光与直立物形成的夹角所造成。从地球是圆球和阳光直线传播这两个前提出发,从假想的地心向塞恩城和亚历山大城引两条直线,其中的夹角应等于亚历山大城的阳光与直立物形成的夹角。按照相似三角形的比例关系,已知两地之间的距离,便能测出地球的圆周长。埃拉托色尼测出夹角约为7度,是地球圆周角(360度)的五十分之一,由此推算地球的周长大约为4万千米,这与实际地球周长(40076千米)相差无几。他还算出太阳与地球间距离为1.47亿千米,和实际距离1.49亿千米也惊人地相近。这充分反映了埃拉托色尼的学说和智慧。
再
见
周长是多少(教材P46~47)
三年级数学·上
新课标[江苏]
第3单元
你们知道“凸”形图形的周长简便算法吗?
把每条边加起来就可以了呀!还有简便算法?
算一个长方形或正方形的面积也可以。
为什么可以这样算?
可以通过移边的方法使它变成规则图形!
知识点1
由几个相同正方形拼成的
图形,周长可能不相等
用6个边长1厘米的正方形可以拼成哪些不同的图形 拼成的图形周长各是多少厘米 它们的周长相等吗
探究方法
(1)用6个边长1厘米的正方形拼出你喜欢的图形。
(2)用算或数的方法,求出所拼图形的周长。
规范解答
(1)摆法一:
周长:1+6=7(厘米)
7×2=14(厘米)
规范解答
周长:3+2=5(厘米)
5×2=10(厘米)
(2)摆法二:
规范解答
周长:2+2+1+2+1+4=12(厘米)
(3)摆法三:
规范解答
(4)摆法四:
周长:2×2+10×1=14(厘米)
从各图中可以看出,拼成的图形周长不相等。
规范解答
周长14厘米
周长10厘米
周长12厘米
周长14厘米
规范解答
周长14厘米
用6个边长1厘米的正方形可以拼成多种不同形状的图形,如上述4种图形,虽然都用了6个相同的小正方形,但是它们的周长可能会不相等。
周长10厘米
周长12厘米
周长14厘米
总结
计算一个图形周长的方法有很多,无论用什么方法算周长,一定要注意周长指的是一个图形外边一周的长度。用同样的正方形拼成不同形状的图形,它们的周长可能相等,也可能不相等。
知识点2
巧求周长
左边两个图形的周长各是多少厘米 它们的周长相等吗 (每个小方格的边长表示1厘米)
猜猜下面图形的周长是多少厘米,
和同学说说你的想法,再计算。
1
2
3
探究方法
方法一 数一数。
数出每个图形的周长是由几个小方格的边长组成的,再计算它们的周长。
图①:1×22=22(厘米)
图②:1×22=22(厘米)
图③:1×22=22(厘米)
三幅图的周长都相等。
探究方法
方法二 通过平移,图②和图③都转化成长6厘米、宽5厘米的长方形,与图①的长和宽相等。它们的周长都等于:(6+5)×2=22(厘米)(如图)。
图②
图③
规范解答
6+5=11(厘米)
11×2=22(厘米)
答:左边两个图形的周长相等,都是22厘米,右边图形的周长也是22厘米。
通过移一移、拼一拼的方法,把不规则图形转化成规则图形后,再按照周长的计算方法来计算就容易多了。
知识点3
画一画
你能在方格纸上画出周长是20厘米的长方形或正方形吗 能画出不同的长方形吗 (每个小方格的边长表示1厘米)
画出的长方形的长、宽各是
多少?正方形的边长呢?
理解题意
因为周长是20厘米,所以长方形的长、宽的和应等于10厘米,我们可以列出下表:
长
9厘米
8厘米
7厘米
6厘米
5厘米
宽
1厘米
2厘米
3厘米
4厘米
5厘米
周长
20厘米
20厘米
20厘米
20厘米
20厘米
正方形周长是20厘米
正方形边长=周长÷4
20÷4=5(厘米)
规范解答
如下图所示。
5厘米
5厘米
9厘米
1厘米
8厘米
2厘米
7厘米
3厘米
6厘米
4厘米
要画出给定周长的长方形,需要先计算出长方形的长与宽之和,才好画出图形;如果是画出正方形,那么需要先用“周长÷4”求出正方形的边长,再画图。
知识点4
估一估,量一量
下面两个图案的周长大约各是多少厘米 先估一估,再量一量。
你是怎样测量的?
你估计的怎么样?
估计 厘米
实际 厘米
估计 厘米
实际 厘米
五角星每边长约1厘米,共有10条边,笑脸的周长约有10厘米。
估算
量一量
用直尺测量出五角星一条边的长是1厘米,它的周长是1×10=10(厘米);用绳子绕笑脸一周,去掉多余的部分,伸直绳子,用直尺测量绳子的长是10厘米,即周长是10厘米。
比较估计与实际测量的结果,看估计是否准确
与同学交流估计方法
1.计算下面图形的周长。(单位:厘米)
同步练习
3+2=5(厘米)
3+5=8(厘米)
8+5=13(厘米)
13×2=26(厘米)
2
5
3
3
2
1
2
3
4
3+1+2=6(厘米)
6+4=10(厘米)
10×2=20(厘米)
20+2+2=24(厘米)
同步练习
2.请你在方格纸上画出周长是12厘米的长方形或正方形。能画出不同的长方形吗 (每个小方格的边长表示1厘米)
5厘米
1厘米
4厘米
2厘米
3厘米
第一个算出地球周长的人
2000多年前,有人用简单的测量工具计算出地球的周长,这个人就是古希腊的埃拉托色尼(约公元前275~前1940)。
埃拉托色尼博学多才,他不仅通晓天文,而且熟知地理;又是诗人、历史学家、语言学家、哲学家,曾担任过亚历山大博物馆的馆长。
细心的埃拉托色尼发现:离亚历山大城约800千米的塞恩城,夏日正午的阳光可以一直照到井底,因而这时候所有地面上的直立物都应该没有影子。但是,亚历山大城地面上的直立物却有一段很短的影子。他认为:直立物的影子是由亚历山大城的阳光与直立物形成的夹角所造成。从地球是圆球和阳光直线传播这两个前提出发,从假想的地心向塞恩城和亚历山大城引两条直线,其中的夹角应等于亚历山大城的阳光与直立物形成的夹角。按照相似三角形的比例关系,已知两地之间的距离,便能测出地球的圆周长。埃拉托色尼测出夹角约为7度,是地球圆周角(360度)的五十分之一,由此推算地球的周长大约为4万千米,这与实际地球周长(40076千米)相差无几。他还算出太阳与地球间距离为1.47亿千米,和实际距离1.49亿千米也惊人地相近。这充分反映了埃拉托色尼的学说和智慧。
再
见
同课章节目录
- 一 两、三位数乘一位数
- 整十、整百数乘一位数的口算
- 倍的认识和有关倍的简单实际问题
- 两、三位数乘一位数(不进位)的笔算
- 两、三位数乘一位数(进位)的笔算
- 两、三位数乘一位数(连续进位)的笔算
- 乘数中间、末尾有0的乘法
- 二 千克和克
- 认识千克
- 认识克
- 三 长方形和正方形
- 长方形和正方形的基本特征
- 认识周长
- 长方形和正方形周长的计算
- 周长是多少
- 四 两、三位数除以一位数
- 两、三位数除以一位数的口算
- 两、三位数除以一位数(首位能整除)的笔算
- 除法的验算
- 两、三位数除以一位数(首位不能整除)的笔算
- 商中间、末尾有0的除法
- 五 解决问题的策略
- 间隔排列
- 六 平移、旋转和轴对称
- 七 分数的初步认识(一)
- 多彩的“分数条”
