湘教版数学九年级上册 3.2 平行线分线段成比例(第1课时) 教案
文档属性
| 名称 | 湘教版数学九年级上册 3.2 平行线分线段成比例(第1课时) 教案 |
|
|
| 格式 | doc | ||
| 文件大小 | 246.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-29 15:47:41 | ||
图片预览


文档简介
课题:3.2
平行线分线段成比例(第1课时)
教学目标:1.理解并掌握平行线分线段成比例的基本事实及其推论,并能用初步应用;
2.培养学生识图能力和推理论证能力;
3.通过动手、观察、思考、交流等活动,培养学生的探索精神及合作意识。
教学重点:平行线分线段成比例的基本事实及推论的应用。
教学难点:平行线分线段成比例的基本事实的理解及推论的应用。
教具学具:多媒体计算机、展台、常用画图工具、横格纸、短绳(线)。
教学过程:
一.创设情境,引入新课
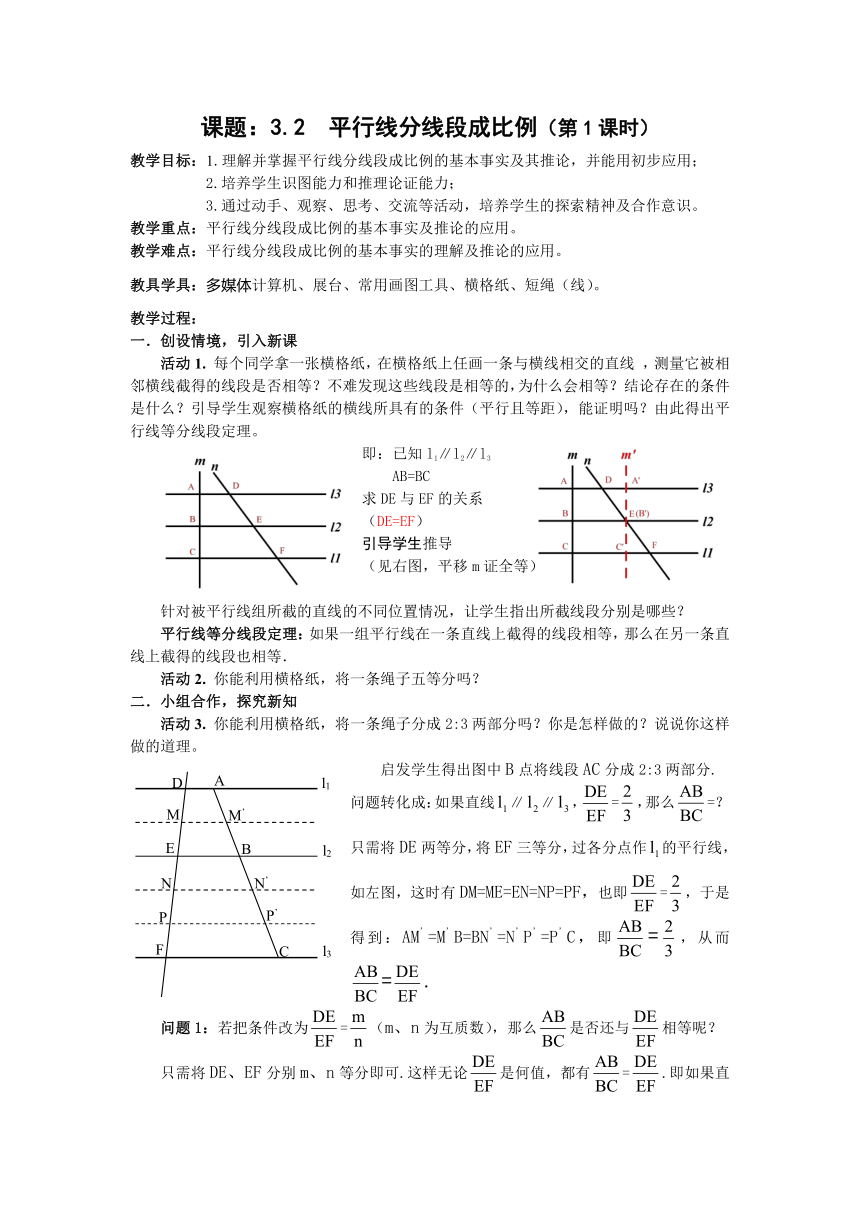
活动1.
每个同学拿一张横格纸,在横格纸上任画一条与横线相交的直线
,测量它被相邻横线截得的线段是否相等?不难发现这些线段是相等的,为什么会相等?结论存在的条件是什么?引导学生观察横格纸的横线所具有的条件(平行且等距),能证明吗?由此得出平行线等分线段定理。
即:已知l1∥l2∥l3
AB=BC
求DE与EF的关系
(DE=EF)
引导学生推导
(见右图,平移m证全等)
针对被平行线组所截的直线的不同位置情况,让学生指出所截线段分别是哪些?
平行线等分线段定理:如果一组平行线在一条直线上截得的线段相等,那么在另一条直线上截得的线段也相等.
活动2.
你能利用横格纸,将一条绳子五等分吗?
二.小组合作,探究新知
活动3.
你能利用横格纸,将一条绳子分成2:3两部分吗?你是怎样做的?说说你这样做的道理。
启发学生得出图中B点将线段AC分成2:3两部分.
问题转化成:如果直线∥∥,=,那么=?
只需将DE两等分,将EF三等分,过各分点作的平行线,如左图,这时有DM=ME=EN=NP=PF,也即=,于是得到:AM’=M’B=BN’=N’P’=P’C,即=,从而=.
问题1:若把条件改为=(m、n为互质数),那么是否还与相等呢?
只需将DE、EF分别m、n等分即可.这样无论是何值,都有=.即如果直线∥∥,那么=.
问题2:比例式,,成立吗?
由此,得到如下基本事实:
平行线分线段成比例定理:两条直线被一组平行线所截,所得的对应线段成比例(简称“平行线分线段成比例”)
理解:①一组:3条及以上,通常为3条
②对应:上对上,下对下,全对全
即:(反比性质亦成立)
活动4.
如图,∥∥,分别就图中各种情况,写出“对应线段成比例”的比例式。
三.变式训练,优化思维
问题3:如图,在△ABC中,点D,E分别在AB,AC上(或BA,CA的延长线上)已知ED∥BC,则,成立吗?为什么?
由此得到以下结论:
推论:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例。
例1.
如图,在△ABC中,D、E分别是AB和AC上的点,且
DE∥BC,
(1)如果AD=3.2cm,
DB=1.2cm
,AE=2.4cm,那么EC的长是多少?
(2)如果AB=5cm,
AD=3cm,AC=4cm
,那么EC的长是多少?
例2.
如图,l1//l2//l3,直线l2与AB,CD分别相交于M,K,过点M的直线EF分别与直线l1,l3相交于点E,F.已知AM=2,MB=3,EM=4,CD=12,求FM,CK,DK的长.
例3.
如图,在△ABC的边BC上任取两点D,E,过点D作AB的平行线交AC于点M,连接AE,过点M作AE的平行线交BC于点N.求证:.
四.当堂训练,知识反馈
1、如图1,若DE//AB,则
,
,
.
2、如图2,若AD//EF//BC,则
=
.
3、如图3,已知平行四边形ABCD,
,
.
4、填括号:
EC=(
)
AE=(
),GC=(
)
AD=(
)
5、如图,在△ABC中,D、E分别是AB和AC上的点,且
DE∥BC,
(1)如果AD=3.2cm,
DB=1.2cm
,AE=2.4cm,那么EC的长是多少?
(2)如果AB=5cm,
AD=3cm,AC=4cm
,那么EC的长是多少?
6、如图,l1//l2//l3,直线l2与AB,CD分别相交于M,K,过点M的直线EF分别与直线l1,l3相交于点E,F.已知AM=2,MB=3,EM=4,CD=12,求FM,CK,DK的长.
7、如图,若l1//l2//l3,DE=3,
EO=2,
OF=4,
OB=1,求:AB、OC的长.
8、如图,在△ABC的边BC上任取两点D,E,过点D作AB的平行线交AC于点M,连接AE,过点M作AE的平行线交BC于点N.求证:.
1.小结本课学习的主要内容;2.谈谈你的学习体会及收获。
六、布置作业,巩固提升
P71
习题3.2
A组
1、2
A
B
E1
F
C
D
P
P’
M
M’
N
N’
l1
l2
l3
l1
l2
l3
A
B
C
D
E
F
G
l1
l2
l3
A
B
C
D
E
l1
l2
l3
A
B
C
D
E
F
G
l1
l2
l3
A
B
C
D
E
X型
A型
A
B
C
D
E
例3图
例2图
图1
图2
图3
4
6
9
9
15
12
10
3
6
4
A
B
C
D
E
6题图
l1
l2
l3
A
B
C
D
E
F
O
7题图
8图
平行线分线段成比例(第1课时)
教学目标:1.理解并掌握平行线分线段成比例的基本事实及其推论,并能用初步应用;
2.培养学生识图能力和推理论证能力;
3.通过动手、观察、思考、交流等活动,培养学生的探索精神及合作意识。
教学重点:平行线分线段成比例的基本事实及推论的应用。
教学难点:平行线分线段成比例的基本事实的理解及推论的应用。
教具学具:多媒体计算机、展台、常用画图工具、横格纸、短绳(线)。
教学过程:
一.创设情境,引入新课
活动1.
每个同学拿一张横格纸,在横格纸上任画一条与横线相交的直线
,测量它被相邻横线截得的线段是否相等?不难发现这些线段是相等的,为什么会相等?结论存在的条件是什么?引导学生观察横格纸的横线所具有的条件(平行且等距),能证明吗?由此得出平行线等分线段定理。
即:已知l1∥l2∥l3
AB=BC
求DE与EF的关系
(DE=EF)
引导学生推导
(见右图,平移m证全等)
针对被平行线组所截的直线的不同位置情况,让学生指出所截线段分别是哪些?
平行线等分线段定理:如果一组平行线在一条直线上截得的线段相等,那么在另一条直线上截得的线段也相等.
活动2.
你能利用横格纸,将一条绳子五等分吗?
二.小组合作,探究新知
活动3.
你能利用横格纸,将一条绳子分成2:3两部分吗?你是怎样做的?说说你这样做的道理。
启发学生得出图中B点将线段AC分成2:3两部分.
问题转化成:如果直线∥∥,=,那么=?
只需将DE两等分,将EF三等分,过各分点作的平行线,如左图,这时有DM=ME=EN=NP=PF,也即=,于是得到:AM’=M’B=BN’=N’P’=P’C,即=,从而=.
问题1:若把条件改为=(m、n为互质数),那么是否还与相等呢?
只需将DE、EF分别m、n等分即可.这样无论是何值,都有=.即如果直线∥∥,那么=.
问题2:比例式,,成立吗?
由此,得到如下基本事实:
平行线分线段成比例定理:两条直线被一组平行线所截,所得的对应线段成比例(简称“平行线分线段成比例”)
理解:①一组:3条及以上,通常为3条
②对应:上对上,下对下,全对全
即:(反比性质亦成立)
活动4.
如图,∥∥,分别就图中各种情况,写出“对应线段成比例”的比例式。
三.变式训练,优化思维
问题3:如图,在△ABC中,点D,E分别在AB,AC上(或BA,CA的延长线上)已知ED∥BC,则,成立吗?为什么?
由此得到以下结论:
推论:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例。
例1.
如图,在△ABC中,D、E分别是AB和AC上的点,且
DE∥BC,
(1)如果AD=3.2cm,
DB=1.2cm
,AE=2.4cm,那么EC的长是多少?
(2)如果AB=5cm,
AD=3cm,AC=4cm
,那么EC的长是多少?
例2.
如图,l1//l2//l3,直线l2与AB,CD分别相交于M,K,过点M的直线EF分别与直线l1,l3相交于点E,F.已知AM=2,MB=3,EM=4,CD=12,求FM,CK,DK的长.
例3.
如图,在△ABC的边BC上任取两点D,E,过点D作AB的平行线交AC于点M,连接AE,过点M作AE的平行线交BC于点N.求证:.
四.当堂训练,知识反馈
1、如图1,若DE//AB,则
,
,
.
2、如图2,若AD//EF//BC,则
=
.
3、如图3,已知平行四边形ABCD,
,
.
4、填括号:
EC=(
)
AE=(
),GC=(
)
AD=(
)
5、如图,在△ABC中,D、E分别是AB和AC上的点,且
DE∥BC,
(1)如果AD=3.2cm,
DB=1.2cm
,AE=2.4cm,那么EC的长是多少?
(2)如果AB=5cm,
AD=3cm,AC=4cm
,那么EC的长是多少?
6、如图,l1//l2//l3,直线l2与AB,CD分别相交于M,K,过点M的直线EF分别与直线l1,l3相交于点E,F.已知AM=2,MB=3,EM=4,CD=12,求FM,CK,DK的长.
7、如图,若l1//l2//l3,DE=3,
EO=2,
OF=4,
OB=1,求:AB、OC的长.
8、如图,在△ABC的边BC上任取两点D,E,过点D作AB的平行线交AC于点M,连接AE,过点M作AE的平行线交BC于点N.求证:.
1.小结本课学习的主要内容;2.谈谈你的学习体会及收获。
六、布置作业,巩固提升
P71
习题3.2
A组
1、2
A
B
E1
F
C
D
P
P’
M
M’
N
N’
l1
l2
l3
l1
l2
l3
A
B
C
D
E
F
G
l1
l2
l3
A
B
C
D
E
l1
l2
l3
A
B
C
D
E
F
G
l1
l2
l3
A
B
C
D
E
X型
A型
A
B
C
D
E
例3图
例2图
图1
图2
图3
4
6
9
9
15
12
10
3
6
4
A
B
C
D
E
6题图
l1
l2
l3
A
B
C
D
E
F
O
7题图
8图
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
