2.3匀变速直线运动位移-时间关系
文档属性
| 名称 | 2.3匀变速直线运动位移-时间关系 |  | |
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2012-07-23 10:44:37 | ||
图片预览








文档简介
(共38张PPT)
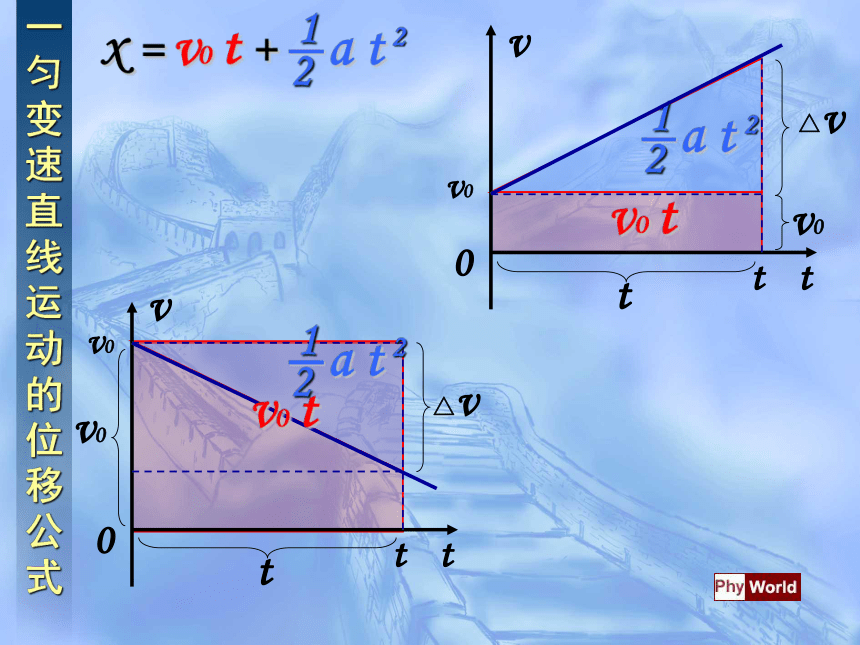
a不变
速度
位移
时间
v=v0+at
?
?
3、匀变速直线运动的位移与时间的关系
思考与讨论:
对于匀变速直线运动,它的位移与它的 v-t 图象,是不是也有类似的关系呢?
匀变速直线运动的位移
V0
V
0
t
t
t1
t2
t3
t4
结论:在匀变速直线运动的 v-t 图象中,物体的位移 x 在数值上等于图线与坐标轴所围的面积。
(横轴上方的面积与横轴下方的面积有什么分别?)
匀变速直线运动位移与时间的关系式(简称位移公式)
匀变速直线运动的位移
V
0
t
t
V0
思考:能否利用上述结论找出匀变速直线运动的位移与时间的关系式呢?
A
B
C
S = ( OC + AB ) ×OA
1
2
—
x = ( v0 + v ) t
1
2
—
v = v0 + a t
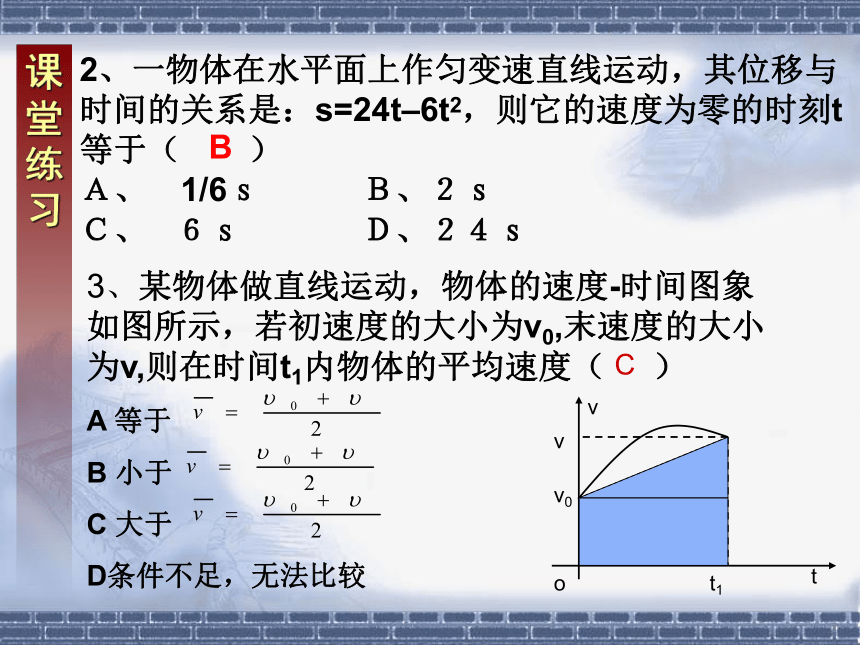
x = v0 t + a t
1
2
—
2
0
v
一匀变速直线运动的位移公式
a t
1
2
—
2
t
v0
△v
x = v0 t + a t
1
2
—
2
v0 t
v
0
t
t
v0
t
v0
△v
v
0
t
t
v0
v0 t
a t
1
2
—
2
说明
1).公式 中的 x 、v0 、
a 均为矢量,应用时必须选取统一方向为正方
向。
x = v0 t + a t
1
2
—
2
v = v0 + a t
x = v0 t + a t
1
2
—
2
2).利用 和
综合应用,可以解决所有的匀变速直线运动。
问题一:匀变速直线运动平均速度、首尾速度、中点时刻速度的关系
由
注:此公式仅对匀变速直线运动成立,非匀变速运动不能使用。
匀变速直线运动平均速度、首尾速度、
中点时刻速度的关系
1、物体的位移随时间变化的函数关系为x=(4t-2t2)m,则它运动的初速度、加速度分别为( )
A 4m/s,-2m/s2 B 4m/s, 2m/s2
C 4m/s,-4m/s2 D 4m/s, 4m/s2
C
课堂练习
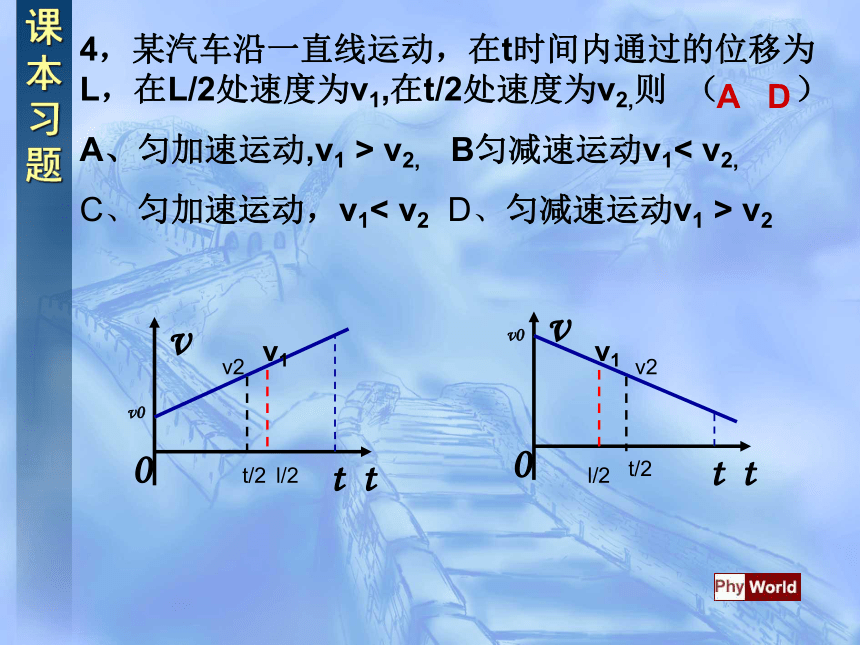
2、一物体在水平面上作匀变速直线运动,其位移与时间的关系是:s=24t–6t2,则它的速度为零的时刻t等于( )
A、 1/6s B、2s
C、 6s D、24s
3、某物体做直线运动,物体的速度-时间图象如图所示,若初速度的大小为v0,末速度的大小为v,则在时间t1内物体的平均速度( )
A 等于
B 小于
C 大于
D条件不足,无法比较
v
v
v0
t1
o
t
C
B
课本习题
4,某汽车沿一直线运动,在t时间内通过的位移为L,在L/2处速度为v1,在t/2处速度为v2,则 ( )
A、匀加速运动,v1 > v2, B匀减速运动v1< v2,
C、匀加速运动,v1< v2 D、匀减速运动v1 > v2
v
0
t
t
v0
v
0
t
t
v0
t/2
v1
v2
v2
v1
A D
l/2
t/2
l/2
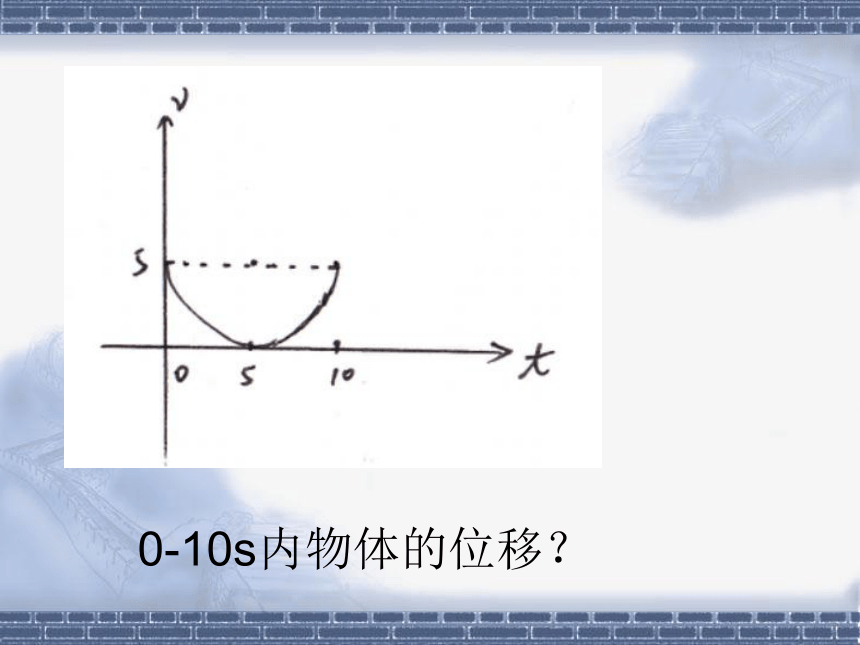
0-10s内物体的位移?
5,一个物体做匀减速直线运V0=60m/s,a=10m/s2,求物体运动100m所需要的时间t。
t=2s或10s
解题技巧
末速度为零的匀减速直线运动可看成初速度为零,加速度大小相等的匀加速直线运动的逆过程。
v0
A
B
0
a
a
已知汽车刹车后10s停下来,且汽车在匀减速直线运动时的加速度大小为1m/s2。
B
A
0
v0
(2)求汽车停止前最后1s内的位移。(0.5m)
(1)求汽车从刹车直到停止时的位移。(50m)
二、写出初速度为0的匀变速直线运动的
位移时间关系式:
x = a t
1
2
—
2
速度时间关系式: v = a t
问:一质点做初速度为0的匀加速直线运动。
(1)ts末、2t末、 3t末‥ ‥ ‥nt 末的速度之比为多少?
由v = a t知,V∝t,故ts末、2t末、 3t末‥ ‥ nt 末的速度之比为:1:2:3: ‥ ‥ n.
(2)t内、2t内、 3t内‥ ‥ ‥nt 内的位移之比为多少?
由 知 , x∝t2,故t内、2t内、 3t内‥ ‥nt 内
的位移之比为:1 : 22 : 32 : …… : n2
(3)第1个ts内、第2个t内、 第3个t内‥‥第n个t内的位移之比为多少?
第1个ts内位移为
第2个t内位移为
第3个ts内的位移为
第nt 内位移为
故第1个ts内、第2个t内、 第3个t内‥‥第n个t内的位移之比为1:3:5:‥‥(2n-1)
从运动起点划分为连续相等位移x,则:
4)、位移x、2x、3x……nx内的时间之比为:
t1 : t2 : t3 : …… :tn= 1 : : : …… :
5)、第1段位移x、第2段位移x、第3段位移x内的时间之比为:
T1 : T2 : T3 : …… = 1 : : : ……
o
x
2x
3x
4x
5x
t1
t2
t3
t4
t5
o
6x
t6
T1
T2
T3
T4
T5
T6
1.一物体作直线运动的速度图象如图所示,则下列说法错误的是
A.前2s内做匀加速直线运动
B.前4s内做匀变速直线运动
C.前4s内的平均速度为2m/s
D.后2s内的加速度为-1.5m/s2
B
2
BD
骑自行车的人以5m/s的初速度匀减速地上一个斜坡,加速度的大小为0.4m/s2,斜坡长30m,骑自行车的人通过斜坡需要多少时间?
为什么通过30m的斜坡用了两个不同的时间?将t1=10s和t2=15s分别代入速度公式v=v0+at计算两个对应的末速度,v1=1m/s和v2=-1m/s.后一个速度v2=-1m/s与上坡的速度方向相反,与实际情况不符,所以应该舍去.实际上,15s是自行车按0.4m/s2的加速度匀减速运动速度减到零又反向加速到1m/s所用的时间,而这15s内的位移恰好也是30m
在本题中,由于斜坡不是足够长,用10s的时间就到达坡顶,自行车不可能倒着下坡,从此以后自行车不再遵循前面的运动规律,所以15s是不合题意的.
答案:10s
点评:由位移公式x=v0t+ at2,求时间t,由于解的是一个一元二次方程,因此会有两个解,这两个解不一定都有意义,解出后一定要进行讨论.
由静止开始做匀加速运动的汽车,头一秒内通过0.4m路程,有以下说法:
①第1s末的速度为0.8m/s
②加速度为0.8m/s2
③第2s内通过的路程为1.2m
④前2s内通过的路程为1.2m
其中正确的是 ( )
A.①②③ B.②③④
C.①②③④ D.①②④
答案:A
一个滑雪的人,从85m长的山坡上匀变速直线滑下(如下图所示),初速度是1.8m/s,末速度是5.0m/s,他通过这段山坡需要多长时间?
答案:25s
答案:B
要求摩托车由静止开始在尽量短的时间内走完一段直道,然后驶入一段半圆形的弯道,但在弯道上行驶时车速不能太快,以免因离心作用而偏出车道.求摩托车在直道上行驶所用的最短时间.有关数据见表格.
启动加速度a1 4m/s2
制动加速度a2 8m/s2
直道最大速度v1 40m/s
弯道最大速度v2 20m/s
直道长度s 218m
代入数据解得
t′1=9s,t′2=2s,s′1=162m,s′2=56m,vm=36m/s
所以最短时间为t=t′1+t′2=11s.
2008年9月25日,中国用长征运载火箭成功地发射了“神舟七号”卫星,下图是某监测系统每隔2.5s拍摄的关于起始加速阶段火箭的一组照片,已知火箭的长度为40m,现在用刻度尺测量照片上的长度关系,结果如图所示,请你估算火箭的加速度a和火箭在照片中第2个像所对应时刻的瞬时速度大小v.
答案:8m/s2;42m/s
解析:从照片上可得,刻度尺的1cm相当于实际长度20m.量出前后两段位移分别为4.00cm和6.50cm,对应的实际位移分别为80m和130m,由Δx=aT2可得a=8m/s2,再根据这5秒内的平均速度等于中间时刻的瞬时速度,可得照片中第2个像对应的速度v=42m/s.
通过图象认识物体运动规律,是我们处理物理问题的重要方法.读图象要首先搞清物理意义,再根据图象物理量的变化确定物体运动规律.
a不变
速度
位移
时间
v=v0+at
?
?
3、匀变速直线运动的位移与时间的关系
思考与讨论:
对于匀变速直线运动,它的位移与它的 v-t 图象,是不是也有类似的关系呢?
匀变速直线运动的位移
V0
V
0
t
t
t1
t2
t3
t4
结论:在匀变速直线运动的 v-t 图象中,物体的位移 x 在数值上等于图线与坐标轴所围的面积。
(横轴上方的面积与横轴下方的面积有什么分别?)
匀变速直线运动位移与时间的关系式(简称位移公式)
匀变速直线运动的位移
V
0
t
t
V0
思考:能否利用上述结论找出匀变速直线运动的位移与时间的关系式呢?
A
B
C
S = ( OC + AB ) ×OA
1
2
—
x = ( v0 + v ) t
1
2
—
v = v0 + a t
x = v0 t + a t
1
2
—
2
0
v
一匀变速直线运动的位移公式
a t
1
2
—
2
t
v0
△v
x = v0 t + a t
1
2
—
2
v0 t
v
0
t
t
v0
t
v0
△v
v
0
t
t
v0
v0 t
a t
1
2
—
2
说明
1).公式 中的 x 、v0 、
a 均为矢量,应用时必须选取统一方向为正方
向。
x = v0 t + a t
1
2
—
2
v = v0 + a t
x = v0 t + a t
1
2
—
2
2).利用 和
综合应用,可以解决所有的匀变速直线运动。
问题一:匀变速直线运动平均速度、首尾速度、中点时刻速度的关系
由
注:此公式仅对匀变速直线运动成立,非匀变速运动不能使用。
匀变速直线运动平均速度、首尾速度、
中点时刻速度的关系
1、物体的位移随时间变化的函数关系为x=(4t-2t2)m,则它运动的初速度、加速度分别为( )
A 4m/s,-2m/s2 B 4m/s, 2m/s2
C 4m/s,-4m/s2 D 4m/s, 4m/s2
C
课堂练习
2、一物体在水平面上作匀变速直线运动,其位移与时间的关系是:s=24t–6t2,则它的速度为零的时刻t等于( )
A、 1/6s B、2s
C、 6s D、24s
3、某物体做直线运动,物体的速度-时间图象如图所示,若初速度的大小为v0,末速度的大小为v,则在时间t1内物体的平均速度( )
A 等于
B 小于
C 大于
D条件不足,无法比较
v
v
v0
t1
o
t
C
B
课本习题
4,某汽车沿一直线运动,在t时间内通过的位移为L,在L/2处速度为v1,在t/2处速度为v2,则 ( )
A、匀加速运动,v1 > v2, B匀减速运动v1< v2,
C、匀加速运动,v1< v2 D、匀减速运动v1 > v2
v
0
t
t
v0
v
0
t
t
v0
t/2
v1
v2
v2
v1
A D
l/2
t/2
l/2
0-10s内物体的位移?
5,一个物体做匀减速直线运V0=60m/s,a=10m/s2,求物体运动100m所需要的时间t。
t=2s或10s
解题技巧
末速度为零的匀减速直线运动可看成初速度为零,加速度大小相等的匀加速直线运动的逆过程。
v0
A
B
0
a
a
已知汽车刹车后10s停下来,且汽车在匀减速直线运动时的加速度大小为1m/s2。
B
A
0
v0
(2)求汽车停止前最后1s内的位移。(0.5m)
(1)求汽车从刹车直到停止时的位移。(50m)
二、写出初速度为0的匀变速直线运动的
位移时间关系式:
x = a t
1
2
—
2
速度时间关系式: v = a t
问:一质点做初速度为0的匀加速直线运动。
(1)ts末、2t末、 3t末‥ ‥ ‥nt 末的速度之比为多少?
由v = a t知,V∝t,故ts末、2t末、 3t末‥ ‥ nt 末的速度之比为:1:2:3: ‥ ‥ n.
(2)t内、2t内、 3t内‥ ‥ ‥nt 内的位移之比为多少?
由 知 , x∝t2,故t内、2t内、 3t内‥ ‥nt 内
的位移之比为:1 : 22 : 32 : …… : n2
(3)第1个ts内、第2个t内、 第3个t内‥‥第n个t内的位移之比为多少?
第1个ts内位移为
第2个t内位移为
第3个ts内的位移为
第nt 内位移为
故第1个ts内、第2个t内、 第3个t内‥‥第n个t内的位移之比为1:3:5:‥‥(2n-1)
从运动起点划分为连续相等位移x,则:
4)、位移x、2x、3x……nx内的时间之比为:
t1 : t2 : t3 : …… :tn= 1 : : : …… :
5)、第1段位移x、第2段位移x、第3段位移x内的时间之比为:
T1 : T2 : T3 : …… = 1 : : : ……
o
x
2x
3x
4x
5x
t1
t2
t3
t4
t5
o
6x
t6
T1
T2
T3
T4
T5
T6
1.一物体作直线运动的速度图象如图所示,则下列说法错误的是
A.前2s内做匀加速直线运动
B.前4s内做匀变速直线运动
C.前4s内的平均速度为2m/s
D.后2s内的加速度为-1.5m/s2
B
2
BD
骑自行车的人以5m/s的初速度匀减速地上一个斜坡,加速度的大小为0.4m/s2,斜坡长30m,骑自行车的人通过斜坡需要多少时间?
为什么通过30m的斜坡用了两个不同的时间?将t1=10s和t2=15s分别代入速度公式v=v0+at计算两个对应的末速度,v1=1m/s和v2=-1m/s.后一个速度v2=-1m/s与上坡的速度方向相反,与实际情况不符,所以应该舍去.实际上,15s是自行车按0.4m/s2的加速度匀减速运动速度减到零又反向加速到1m/s所用的时间,而这15s内的位移恰好也是30m
在本题中,由于斜坡不是足够长,用10s的时间就到达坡顶,自行车不可能倒着下坡,从此以后自行车不再遵循前面的运动规律,所以15s是不合题意的.
答案:10s
点评:由位移公式x=v0t+ at2,求时间t,由于解的是一个一元二次方程,因此会有两个解,这两个解不一定都有意义,解出后一定要进行讨论.
由静止开始做匀加速运动的汽车,头一秒内通过0.4m路程,有以下说法:
①第1s末的速度为0.8m/s
②加速度为0.8m/s2
③第2s内通过的路程为1.2m
④前2s内通过的路程为1.2m
其中正确的是 ( )
A.①②③ B.②③④
C.①②③④ D.①②④
答案:A
一个滑雪的人,从85m长的山坡上匀变速直线滑下(如下图所示),初速度是1.8m/s,末速度是5.0m/s,他通过这段山坡需要多长时间?
答案:25s
答案:B
要求摩托车由静止开始在尽量短的时间内走完一段直道,然后驶入一段半圆形的弯道,但在弯道上行驶时车速不能太快,以免因离心作用而偏出车道.求摩托车在直道上行驶所用的最短时间.有关数据见表格.
启动加速度a1 4m/s2
制动加速度a2 8m/s2
直道最大速度v1 40m/s
弯道最大速度v2 20m/s
直道长度s 218m
代入数据解得
t′1=9s,t′2=2s,s′1=162m,s′2=56m,vm=36m/s
所以最短时间为t=t′1+t′2=11s.
2008年9月25日,中国用长征运载火箭成功地发射了“神舟七号”卫星,下图是某监测系统每隔2.5s拍摄的关于起始加速阶段火箭的一组照片,已知火箭的长度为40m,现在用刻度尺测量照片上的长度关系,结果如图所示,请你估算火箭的加速度a和火箭在照片中第2个像所对应时刻的瞬时速度大小v.
答案:8m/s2;42m/s
解析:从照片上可得,刻度尺的1cm相当于实际长度20m.量出前后两段位移分别为4.00cm和6.50cm,对应的实际位移分别为80m和130m,由Δx=aT2可得a=8m/s2,再根据这5秒内的平均速度等于中间时刻的瞬时速度,可得照片中第2个像对应的速度v=42m/s.
通过图象认识物体运动规律,是我们处理物理问题的重要方法.读图象要首先搞清物理意义,再根据图象物理量的变化确定物体运动规律.
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
