2021-2022学年冀教版数学七年级上册1.10有理数的乘方课件(共22张PPT)
文档属性
| 名称 | 2021-2022学年冀教版数学七年级上册1.10有理数的乘方课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-30 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
1.10
有理数的乘方
冀教版七上
第一章
有理数
学
习
目
标
1.
理解并掌握有理数乘方的意义,知道有理数的乘方和乘法之间的关系.
2.能准确进行有理数的乘方计算.
冀教版七上
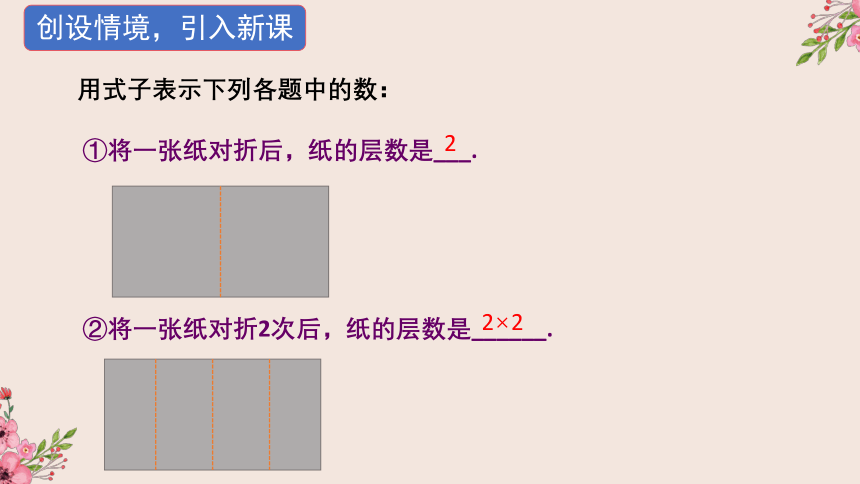
创设情境,引入新课
①将一张纸对折后,纸的层数是___.
②将一张纸对折2次后,纸的层数是______.
用式子表示下列各题中的数:
2
2×2
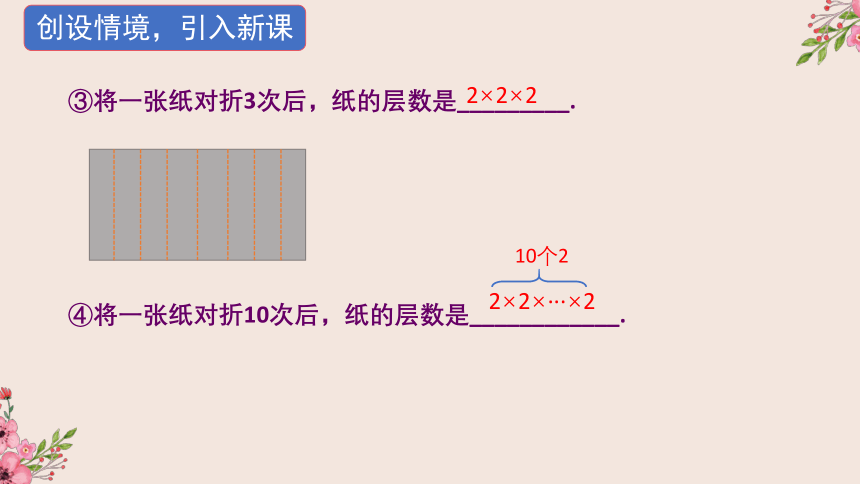
创设情境,引入新课
③将一张纸对折3次后,纸的层数是_________.
④将一张纸对折10次后,纸的层数是____________.
2×2×2
2×2×···×2
10个2
创设情境,引入新课
我们知道,2+2+2+2+2=5×2
那么几个相同的数相乘,可以怎么表示呢?
即:
几个相同的数相加,可以转化为乘法计算.
一般地:
2×2=2
2×2×2=2
2×2×...×2=2
10个2
创设情境,引入新课
仿照前面的例子,完成下列填空:
4×4×4
(-6)×(-6)
注意:添加括号
新课学习
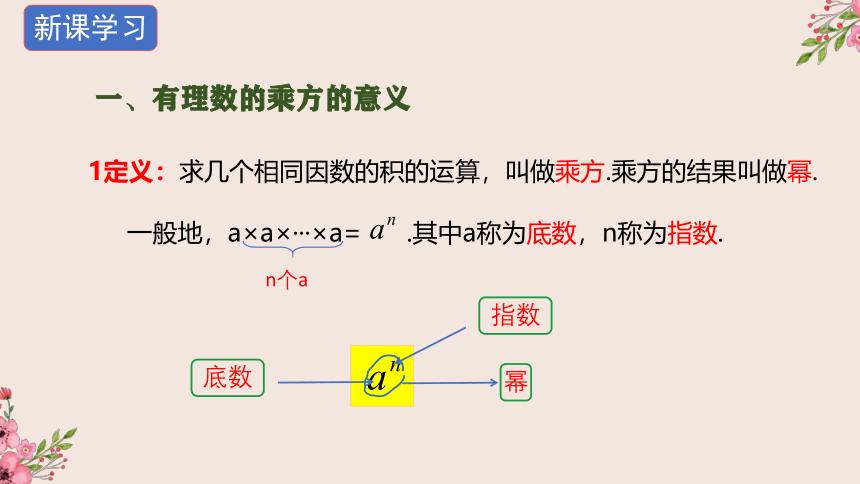
一、有理数的乘方的意义
1定义:求几个相同因数的积的运算,叫做乘方.乘方的结果叫做幂.
一般地,a×a×···×a=
.其中a称为底数,n称为指数.
n个a
指数
底数
幂
新课学习
一、有理数的乘方的意义
2.读法和意义:
读作a的n次方.
表示n个a相乘.
如:
读作___________.
表示___________.
读作___________.
表示___________.
一般地:
还可以读作3的立方.
还可以读作3的平方.
指数为1时,省略不写.
3的4次方
4个3相乘
-1的5次方
5个-1相乘
新课学习
一、有理数的乘方的意义
3.乘方的算法:
如:
=3×3×3×3=81
根据乘方的意义,转化为乘法计算.
=(-1)×(-1)×(-1)×(-1)×(-1)=-1
一起探究
完成下列计算,说说你的发现
想一想:
结果的符号,与什么相关?
底数为正数时,结果__________.
底数为负数时,指数为奇数时,结果_____,指数为偶数时,结果_____.
为正
为正
为负
1
1
1
1
1
1
1
1
1
-1
-1
-1
新课学习
二、有理数乘方的符号法则
正数的任何次幂都是正数;负数的奇次幂是负数,偶次幂是正数.
特别的:
①1的任何次幂都是1.
②-1的奇次幂是-1,偶次幂是1.
典例精析
例1.计算:
注意:
(1)先确定符号;
(2)底数为带分数时,先化为假分数.
典例精析
例2.说出下列各式表示的意义,再计算出结果.
解:
注意:
当n为偶数时,两者互为相反数,当n为奇数时,两者相等.
典例精析
例3.计算.
解:
注意:
巩固练习
①②③⑤
1.给出下列关于
的说法:
①读作a的n次幂;
②表示n个a相乘;
③读作a的n次方;
④表示n个a相加;
⑤a为底数,n为指数.
其中正确的说法有__________.(填序号)
巩固练习
D
3.下列各式成立的是(
).
D
巩固练习
4.一个有理数的平方等于它本身,那么这个有理数是(
).
A.0
B.1
C.±1
D.0和1
D
-1
巩固练习
6.计算:
巩固练习
7.观察下列各式:
······
(1)由此我们可以得出结论:
(2)利用以上信息计算:
课堂小测
8.如图,将一个边长为1的正方形纸片分割成7个部分,部分①是边长为1的正方形纸片面积的一半,部分②是部分①面积的一半,部分③是部分②面积的一半,以此类推,阴影部分的面积是____;受次启发,
①
②
③
④
⑤
⑥
课堂小结
一、有理数的乘方
a×a×···×a=
.其中a称为底数,n称为指数.
n个a
求几个相同因数的积的运算,叫做乘方.乘方的结果叫做幂.
二、有理数乘方的符号法则
正数的任何次幂都是正数;负数的奇次幂是负数,偶次幂是正数.
同学们再见
1.10
有理数的乘方
冀教版七上
第一章
有理数
学
习
目
标
1.
理解并掌握有理数乘方的意义,知道有理数的乘方和乘法之间的关系.
2.能准确进行有理数的乘方计算.
冀教版七上
创设情境,引入新课
①将一张纸对折后,纸的层数是___.
②将一张纸对折2次后,纸的层数是______.
用式子表示下列各题中的数:
2
2×2
创设情境,引入新课
③将一张纸对折3次后,纸的层数是_________.
④将一张纸对折10次后,纸的层数是____________.
2×2×2
2×2×···×2
10个2
创设情境,引入新课
我们知道,2+2+2+2+2=5×2
那么几个相同的数相乘,可以怎么表示呢?
即:
几个相同的数相加,可以转化为乘法计算.
一般地:
2×2=2
2×2×2=2
2×2×...×2=2
10个2
创设情境,引入新课
仿照前面的例子,完成下列填空:
4×4×4
(-6)×(-6)
注意:添加括号
新课学习
一、有理数的乘方的意义
1定义:求几个相同因数的积的运算,叫做乘方.乘方的结果叫做幂.
一般地,a×a×···×a=
.其中a称为底数,n称为指数.
n个a
指数
底数
幂
新课学习
一、有理数的乘方的意义
2.读法和意义:
读作a的n次方.
表示n个a相乘.
如:
读作___________.
表示___________.
读作___________.
表示___________.
一般地:
还可以读作3的立方.
还可以读作3的平方.
指数为1时,省略不写.
3的4次方
4个3相乘
-1的5次方
5个-1相乘
新课学习
一、有理数的乘方的意义
3.乘方的算法:
如:
=3×3×3×3=81
根据乘方的意义,转化为乘法计算.
=(-1)×(-1)×(-1)×(-1)×(-1)=-1
一起探究
完成下列计算,说说你的发现
想一想:
结果的符号,与什么相关?
底数为正数时,结果__________.
底数为负数时,指数为奇数时,结果_____,指数为偶数时,结果_____.
为正
为正
为负
1
1
1
1
1
1
1
1
1
-1
-1
-1
新课学习
二、有理数乘方的符号法则
正数的任何次幂都是正数;负数的奇次幂是负数,偶次幂是正数.
特别的:
①1的任何次幂都是1.
②-1的奇次幂是-1,偶次幂是1.
典例精析
例1.计算:
注意:
(1)先确定符号;
(2)底数为带分数时,先化为假分数.
典例精析
例2.说出下列各式表示的意义,再计算出结果.
解:
注意:
当n为偶数时,两者互为相反数,当n为奇数时,两者相等.
典例精析
例3.计算.
解:
注意:
巩固练习
①②③⑤
1.给出下列关于
的说法:
①读作a的n次幂;
②表示n个a相乘;
③读作a的n次方;
④表示n个a相加;
⑤a为底数,n为指数.
其中正确的说法有__________.(填序号)
巩固练习
D
3.下列各式成立的是(
).
D
巩固练习
4.一个有理数的平方等于它本身,那么这个有理数是(
).
A.0
B.1
C.±1
D.0和1
D
-1
巩固练习
6.计算:
巩固练习
7.观察下列各式:
······
(1)由此我们可以得出结论:
(2)利用以上信息计算:
课堂小测
8.如图,将一个边长为1的正方形纸片分割成7个部分,部分①是边长为1的正方形纸片面积的一半,部分②是部分①面积的一半,部分③是部分②面积的一半,以此类推,阴影部分的面积是____;受次启发,
①
②
③
④
⑤
⑥
课堂小结
一、有理数的乘方
a×a×···×a=
.其中a称为底数,n称为指数.
n个a
求几个相同因数的积的运算,叫做乘方.乘方的结果叫做幂.
二、有理数乘方的符号法则
正数的任何次幂都是正数;负数的奇次幂是负数,偶次幂是正数.
同学们再见
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
