沪教版(上海)数学高三上册-14.2 空间直线与直线的位置关系 (教案)
文档属性
| 名称 | 沪教版(上海)数学高三上册-14.2 空间直线与直线的位置关系 (教案) |

|
|
| 格式 | doc | ||
| 文件大小 | 131.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-09 00:00:00 | ||
图片预览

文档简介
空间直线与直线的位置关系
【教学目标】
1.掌握公理4在常见几何体内(如长方体、正方体等),能快速应用公理,找到问题突破口,寻找作为中间桥梁的直线。
2.学会利用公理4画出几何体的截面。
3.在公理4和定理的推导过程中,着重对初中知识的复习和掌握,引导同学大胆推测,尝试科学的探索精神。在空间四边形的中点、中位线图形中进行推广和证明。
【教学重难点】
1.重点:公理4等角定理及其应用。
2.难点:寻找平行四边形解决有关平行的证明题,等角定理的应用。
【教学过程】
一、引入课题
从生活实例中寻找空间中平行的传递性。
二、讲授新课
1.公理4:
问题1:平面中直线的平行传递性?
问题2:利用教室内实例寻找空间中直线平行的传递性。
公理4:平行于同一直线的两条直线相互平行。
。
公理分析:要证明空间两条直线平行,要找到中间桥梁。
2.等角定理:
问题1:之前学习的等角定理?如果两条相交直线与另两条相交直线分别平行,那么这两组相交直线所成角相等或互补。
问题2:在空间中,这个定理仍然成立吗?
等角定理:如果两条相交直线与另两条相交直线分别平行,那么这两组相交直线所成的锐角(或直角)相等。
注意表述上区别:平面几何合立体几何中某些理论上的不一致应引起学生掌握理论时的重视。
3.例题分析:
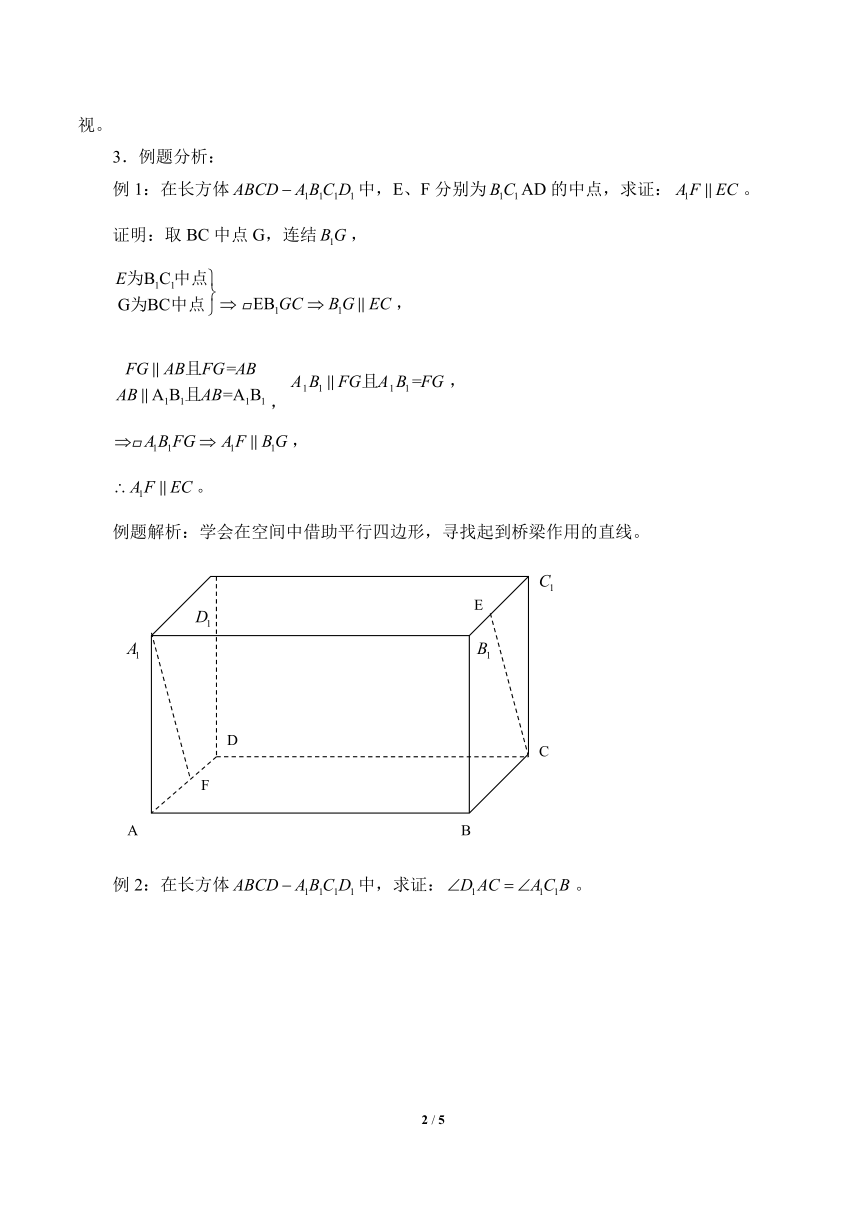
例1:在长方体中,E、F分别为AD的中点,求证:。
证明:取BC中点G,连结,
,
,,
,
。
例题解析:学会在空间中借助平行四边形,寻找起到桥梁作用的直线。
例2:在长方体中,求证:。
证明:,
,
是锐角,。
说明:掌握在空间中利用直线的平行来证明角相等。
4.问题拓展:
(1)空间四边形。
空间四边形相关知识复习:在空间四边形ABCD中,E、H分别为AB.AD中点,F、G为CB.CD三等分点,且。求证:EF,HG,AC三线共点。
说明:复习公理1、2,对于空间四边形——这一立体几何内的新事物,进行回顾和整理,为下一步更好学习做好准备。
例3:已知E、F、G、H分别是空间四边形ABCD各边中点。
①判断四边形EFGH形状;(答:平行四边形。通过公理4。)
②若空间四边形中对角线AC=BD,判断四边形EFGH形状;(答:菱形。平行四边形对角线相互垂直。)
③四边形EFGH什么情况下为矩形?(答:对角线相互垂直,即。)
④结合②、③,可得正方形EFGH;
⑤第②、③、④题的逆命题是否成立?该如何求证?
如②若四边形EFGH中,,则AC=BD。
⑥若E、H分别为AB.AD中点,F、G为CB.CD三等分点,且,判断四边形EFGH形状。(梯形EFGH)
证明:E、H分别为AB.AD中点,
梯形EFGH。
说明:这是空间两条直线平行——公理4的典型应用,加以推测、证明的重要应用。
(2)对于平面图形的结论:
有些可推广到立体图形并有完全相同的结论;
有些在立体图形中有相似的结论,但不完全相同;
有些在立体中则有完全不同的结论。
三、课堂小结
1.空间两条直线平行的判定。
2.空间中等角定理得由来与应用。
3.空间四边形各边中点的相关问题。
4.平面几何与立体几何结论间的比较与联系。
【作业布置】
1.在正方体中,点E、F分别是中点,判断四边形的形状并加以证明。
2.正方体中,E、F分别为AB、BC中点,试画出过点E、F、的截面。
3.在正方体中,点E、F分别在AB、AD上,点G,H分别在上,且满足,联结,
求证:。
4.空间四边形ABCD的各边中点依次为E、F、G、H,连结EG、FH。
(1)求证:EG与HF互相平分;
(2)若BD=2,AC=4,求的值。
5.如图:在空间四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,若AC+BD=m,AC+BD=n,则=
。
6.如图,A是ΔBCD所在平面外一点,M,N分别是ΔABC和ΔACD的重心,若BD=6,求MN的长。
B
A
A
B
B
D
C
B
E
F
A
B
B
D
C
B
A
B
A
B
D
C
E
H
F
G
A
A
A
A
D
F
C
E
B
A
A
B
C
D
A
B
C
D
M
N
E
F
1
/
1
【教学目标】
1.掌握公理4在常见几何体内(如长方体、正方体等),能快速应用公理,找到问题突破口,寻找作为中间桥梁的直线。
2.学会利用公理4画出几何体的截面。
3.在公理4和定理的推导过程中,着重对初中知识的复习和掌握,引导同学大胆推测,尝试科学的探索精神。在空间四边形的中点、中位线图形中进行推广和证明。
【教学重难点】
1.重点:公理4等角定理及其应用。
2.难点:寻找平行四边形解决有关平行的证明题,等角定理的应用。
【教学过程】
一、引入课题
从生活实例中寻找空间中平行的传递性。
二、讲授新课
1.公理4:
问题1:平面中直线的平行传递性?
问题2:利用教室内实例寻找空间中直线平行的传递性。
公理4:平行于同一直线的两条直线相互平行。
。
公理分析:要证明空间两条直线平行,要找到中间桥梁。
2.等角定理:
问题1:之前学习的等角定理?如果两条相交直线与另两条相交直线分别平行,那么这两组相交直线所成角相等或互补。
问题2:在空间中,这个定理仍然成立吗?
等角定理:如果两条相交直线与另两条相交直线分别平行,那么这两组相交直线所成的锐角(或直角)相等。
注意表述上区别:平面几何合立体几何中某些理论上的不一致应引起学生掌握理论时的重视。
3.例题分析:
例1:在长方体中,E、F分别为AD的中点,求证:。
证明:取BC中点G,连结,
,
,,
,
。
例题解析:学会在空间中借助平行四边形,寻找起到桥梁作用的直线。
例2:在长方体中,求证:。
证明:,
,
是锐角,。
说明:掌握在空间中利用直线的平行来证明角相等。
4.问题拓展:
(1)空间四边形。
空间四边形相关知识复习:在空间四边形ABCD中,E、H分别为AB.AD中点,F、G为CB.CD三等分点,且。求证:EF,HG,AC三线共点。
说明:复习公理1、2,对于空间四边形——这一立体几何内的新事物,进行回顾和整理,为下一步更好学习做好准备。
例3:已知E、F、G、H分别是空间四边形ABCD各边中点。
①判断四边形EFGH形状;(答:平行四边形。通过公理4。)
②若空间四边形中对角线AC=BD,判断四边形EFGH形状;(答:菱形。平行四边形对角线相互垂直。)
③四边形EFGH什么情况下为矩形?(答:对角线相互垂直,即。)
④结合②、③,可得正方形EFGH;
⑤第②、③、④题的逆命题是否成立?该如何求证?
如②若四边形EFGH中,,则AC=BD。
⑥若E、H分别为AB.AD中点,F、G为CB.CD三等分点,且,判断四边形EFGH形状。(梯形EFGH)
证明:E、H分别为AB.AD中点,
梯形EFGH。
说明:这是空间两条直线平行——公理4的典型应用,加以推测、证明的重要应用。
(2)对于平面图形的结论:
有些可推广到立体图形并有完全相同的结论;
有些在立体图形中有相似的结论,但不完全相同;
有些在立体中则有完全不同的结论。
三、课堂小结
1.空间两条直线平行的判定。
2.空间中等角定理得由来与应用。
3.空间四边形各边中点的相关问题。
4.平面几何与立体几何结论间的比较与联系。
【作业布置】
1.在正方体中,点E、F分别是中点,判断四边形的形状并加以证明。
2.正方体中,E、F分别为AB、BC中点,试画出过点E、F、的截面。
3.在正方体中,点E、F分别在AB、AD上,点G,H分别在上,且满足,联结,
求证:。
4.空间四边形ABCD的各边中点依次为E、F、G、H,连结EG、FH。
(1)求证:EG与HF互相平分;
(2)若BD=2,AC=4,求的值。
5.如图:在空间四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,若AC+BD=m,AC+BD=n,则=
。
6.如图,A是ΔBCD所在平面外一点,M,N分别是ΔABC和ΔACD的重心,若BD=6,求MN的长。
B
A
A
B
B
D
C
B
E
F
A
B
B
D
C
B
A
B
A
B
D
C
E
H
F
G
A
A
A
A
D
F
C
E
B
A
A
B
C
D
A
B
C
D
M
N
E
F
1
/
1
